- 2021-05-13 发布 |
- 37.5 KB |
- 15页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考数学一轮复习共87节212 空间向量的应用1
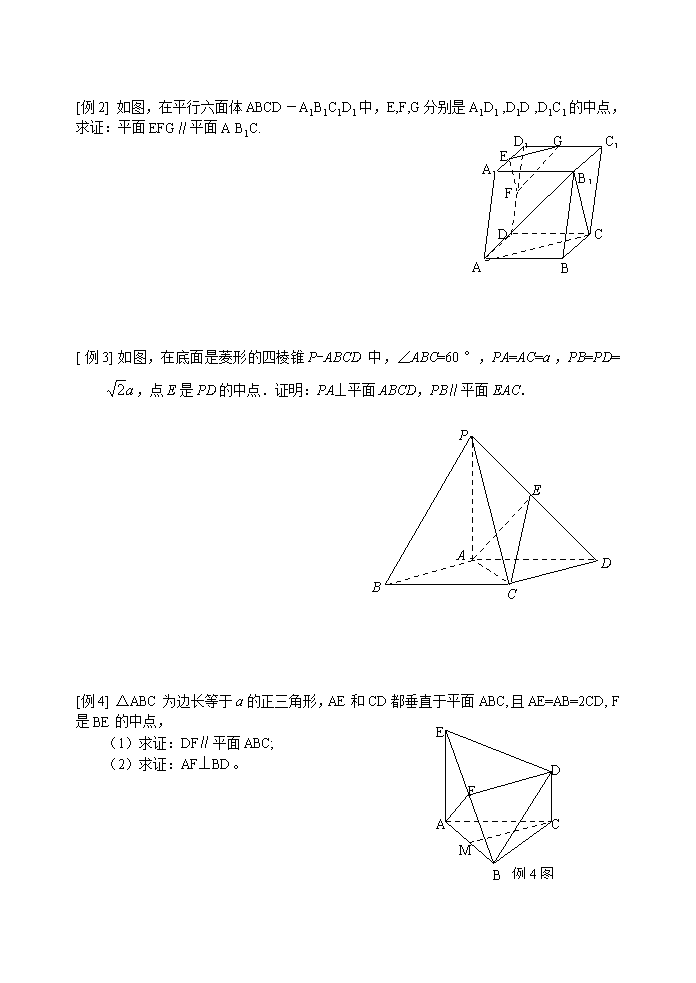
21、空间向量与立体几何 21.2 空间向量的应用(1) 【知识网络】 1. 理解直线的方向向量与平面的法向量的意义;会用待定系数法求平面的法向量。 2. 能用向量语言表述线线、线面、面面的垂直和平行关系。 3. 能用向量方法证明有关线、面位置关系的一些定理(包括三垂线定理);能用向量方法判断一些简单的空间线面的平行和垂直关系。 【典型例题】 [例1](1)a,b是两个非零的向量,a,b是两个平面,下列命题正确的是 ( ) A. ∥的必要条件是是共面向量 B. 是共面向量,则∥ C. ∥a,∥b,则a∥b D. ∥a,b,则不是共面向量 (2)关于直线、与平面、,有下列四个命题: ①且,则; ②且,则; ③且,则; ④且,则. 其中真命题的序号是 ( ) A. ①、② B. ③、④ C. ①、④ D. ②、③ (3)设A、B、C、D是空间不共面的四点,且满足,则△BCD是 (C ) A.钝角三角形 B.直角三角形 C.锐角三角形 D.等腰直角三角形 (4)空间中两个有一条公共边AD的正方形ABCD与ADEF,设M,N分别是BD和AE的中点,给出如下命题: ①AD⊥MN; ②MN∥面CDE; ③MN∥CE; ④MN,CE异面 则所有的正确命题为 。 (5)已知PD垂直正方形ABCD所在平面,AB=2,E是PB的中点,,>. 以DA、DC、DP所在直线分别为x轴、y轴、z轴建立空间坐标系,则点E的坐标为 ;又在平面PAD内有一点F,当点F是 时, EF⊥平面PCB. D B C D1 C1 A A1 B1 G E F [例2] 如图,在平行六面体ABCD-A1B1C1D1中,E,F,G分别是A1D1 ,D1D ,D1C1的中点,求证:平面EFG∥平面A B1C. [例3]如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=,点E是PD的中点.证明:PA⊥平面ABCD,PB∥平面EAC. D E B A C P A C M F B 例4图 D E [例4] △ABC为边长等于a的正三角形,AE和CD都垂直于平面ABC,且AE=AB=2CD,F是BE的中点, (1)求证:DF∥平面ABC; (2)求证:AF⊥BD。 【课内练习】 1. 设是平面外一点,点满足条件,则直线 ( ) A.与平面平行 B.是平面的斜线 C.是平面的垂线 D.在平面内 2. 已知四边形ABCD满足,,,,,则该四边形ABCD为 ( ) A.平行四边形 B.空间四边形 C.平面四边形 D.梯形 3. 已知非零向量及平面,若向量是平面的法向量,则是向量所在直线平行于平面或在平面内的 ( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 4. 已知四面体ABCD中,AB、AC、AD两两互相垂直,给出下列两个命题: ①; ②=. 则下列关于以上两个命题的真假性判断正确的为 ( ) A.①真、②真 B.①真、②假 C.①假、②假 D.①假、②真 5. AB是圆O的直径,PA垂直于圆O所在的平面,C是圆周上不同于点A,B的任一点,连结AC,BC,PB,PC,则在四面体P—ABC中,共有 对互相垂直的平面。 6. 在四面体ABCD中,M,N分别是△ACD与△BCD的重心,则四面体的四个表面中,与MN平行的平面是 。 7. 在直三棱柱中,.有下列条件:①;②;③.其中能成为的充要条件的是(填上该条件的序号)_________. 第8题 8. 如图,已知四面体中,分别为的中点,若,求证:. 9. 正四棱柱AC1中,E为棱D1D上的点,O是底面正方形ABCD的中心. 若,证明O点在面AEB1上的射影是的垂心. 10. 如图,在四棱锥P—ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F. B A C D E F P G 第10题 (1)证明PA//平面EDB; (2)证明PB⊥平面EFD; (3)求二面角C—PB—D的大小. 21、空间向量与立体几何 21.2 空间向量的应用(1) A组 1. 已知=,=,则以为邻边的平行四边形的面积为 ( ) A. B. C.4 D.8 2. 设、是平面a内的两个非零向量,则,是为平面a的法向量的 ( ) A.充分条件 B.充要条件 C.必要条件 D.既非充分又非必要条件 3. 在正方体ABCD-A1B1C1D1中,PQ是异面直线A1D与AC的公垂线,则直线PQ与BD1的关系是 ( ) A.异面直线 B。平行直线 C。垂直不相交 D。垂直且相交 4. 若A(-1,2,3)、B(2,-4,1)、C(x,-1,-3)是直角三角形的三个顶点,则x= . 5. 过一个平面的垂线和这个平面垂直的平面有 个。 6. 如图所示,在棱长为a的正方体OABC-O1A1B1C1中,E、F分别是棱AB、BC边上的动点,且AE=BF.求证:; O A 第6题图 A1 F E C B O1 C1 B1 F E D C B A S 第7题 7. 如图,在五棱锥S—ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,,. 证明:BC⊥平面SAB. 第8题 8. 如图,四棱锥中,平面,与平面所成的角为,在四边形中,,. (1)建立适当的坐标系,写出点的坐标; (2)若的中点为,求证:平面平面. 21、空间向量与立体几何 21.2 空间向量的应用(1) B组 1. A B D C A C B D 第1题图 如图,以等腰直角三角形斜边BC上的高AD为折痕,把△ABD和△ACD折成互相垂直的两个平面后,某学生得出下列四个结论: ①; ②∠BAC=60°; ③三棱锥D—ABC是正三棱锥; ④平面ADC的法向量和平面ABC的法向量互相垂直. 其中正确的是 ( ) A.①② B.②③ C.③④ D.①④ 2. 若,,(),∥,则与一定 ( ) A.共线 B.相交 C.垂直 D。不共面 3. 已知直线a平行于平面a,且它们的距离为d,则到直线a与到平面a的距离都等于d的点的集合是 ( ) A.两条平行直线 B.空集 C.一条直线 D.一个平面 4. 已知直线l⊥面M,直线mÌ平面N,给出下面的命题: ①若面M∥面N,则l⊥m; ②若面M⊥面N,则l∥m; ③若l∥m,则面M⊥面N; ④若l⊥m,则面M∥面N。 其中所有正确命题的序号为 。 5. 已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB==1,则M是线段EF的中点。则AM与平面BDE所成的角为 ,AM与平面BDF所成的角为 。 6. 已和四边形是矩形,,. 第6题 (1)证明:; (2)若, 求证:. 7. 已知矩形,平面,分别是的中点, .能否确定,使直线是直线与的公垂线?若能确定,求出的值;若不能确定,说明理由. 第8题 8. 如图所示,已知四棱锥中,底面是矩形,底面,,为棱上一点,且,问是否存在实数,使平面? 参考答案 21.2 空间向量的应用(1) 【典型例题】 [例1](1)A. (2)D. (3)C.提示:AB、AC、AD两两垂直.用AB、AC、AD的长度分别表示△BCD中三边的长,后用余弦定理得△BCD的每一个内角均为锐角. (4)①②③。 (5)(1,1,1);点F是AD的中点. [例2]设=a, =b, =c,则 =+=+=b + a, =+= a+b, ∴=2,故∥,即EG∥AC. 又=+=+=b-c, =+ = b-c =2,∴ ∥, 即EF∥B1C . 又∵FG∩EF=F, AC∩B1C=C, ∴平面EFG∥平面A B1C. [例3]先证明PA⊥平面ABCD. 建立空间直角坐标系A-xyz,则 A(0,0,0),B(),D(0,a,0),P(0,0,a),于是, ,=(),=(0,a,0). D E P B A C O G H z y x ∵=0+0+0=0,=0+0+0=0, ∴AP⊥AB,AP⊥AD. ∵AB、AD为平面ABCD内的两相交直线, ∴AP⊥平面ABCD. 再证明PB∥平面EAC. 因为 , 所以、、共面. 又PBË平面EAC,所以PB∥平面EAC. [例4](1)取AB的中点M,连接CM. =() =() =() =() =()=。 ∴DF∥CM,又BFË平面ABC,CMÌ平面ABC,∴DF∥平面ABC . (2)= (),,, ∴=()×()=(-) =()=() =(-a2+a2)=0, ∴AF⊥BD 。 【课内练习】 1. D。 2. B。 3. C。 4. A。提示:由AB⊥AC、AB⊥AD,得AB⊥平面ACD,故AB⊥CD,即有.同理,.于是,命题①为真命题.又以AB、AC、AD为同一顶点出发的三条棱,构造长方体,则为自点A的出发的长方体的对角线所在的向量,从而易知命题②亦真. 5. 3。 6. 平面ABC,平面ABD。 7. ③。 8. ∵是的中点,连结,则有, 同理,由是的中点,得. ∵, . ∴ . ∵,∴,即. 9. 设O点在面AEB1上的射影为H,则是面AEB1的法向量. O B1 H E A 易证 面BDD1B1,故. 于是,. ∴. 同理,. ∴H为的垂心. 10.以D为坐标原点,DA,DC,DP分别为x,y,z轴建立空间直角坐标系。设. (1)连结AC,AC交BD于G,连结EG.依题意得. ∵底面ABCD是正方形, ∴G是此正方形的中心,故点G的坐标为, 且. ∴,这表明PA//EG. 而平面EDB且平面EDB,∴PA//平面EDB. (2)依题意得,. 又,故.∴. 由已知,且,所以平面EFD. (3)设点F的坐标为,,则, 从而,所以 . 由条件知,,即,解得,∴点F的坐标为,且, ∴,即,故是二面角C—PB—D的平面角. ∵,,, ∴,得. 所以二面角C—PB—D的大小为. 21.2 空间向量的应用(1) A组 1.A. 2. C。 3. B。 4. 或-11。 5. 无数。 6. 以O为原点,OA为x轴,OC为y轴,OO1为z轴,建立空间直角坐标系O-xyz,则 A1(a,0,a),C1(0,a,a). 设E(a,t,0),F(a-t,a,0),0≤t≤a. ∴,. ∴. ∴. 7. 以A为原点,AB、AS边所在的直线分别为x轴、z轴,以平面ABC内垂直于AB的直线为y轴,建立空间直角坐标系,则A(0,0,0),B(2,0,0),S(0,0,2),且C(2,,0). ∴, ∴,, ∴.,∴. 8. (1)分别以射线为轴建立空间直角坐标系. ∵,,∴. 由平面,得为与平面所成的角,∴. 在直角三角形中,由,得,∴. (2)∵为的中点,∴点的坐标为, ,. ∵,, ∴,∴,又, ∴平面平面. B组 1. B。 2. C。 3. A。提示:与a平行的在a两侧的两条平行直线,且a与这两条平行直线共面于一个与a平行的平面. 4. ①③。 5. 0º,90º。 6. 以为原点,为轴,为轴,为轴,建立空间直角坐标系.设,,,则,,,. (1)∵,∴,. ∴,, 故,∴,即. (2)∵,,∴, ∴所成二面角的平面角,即,∴. 于是有,,,. ∴,即, ,即. ∴. 7. 以点为原点建立空间直角坐标系(如图所示),设点、、、,那么、、. ∴,,. ∵,∴,即恒成立. 若,则 , 则.因为是锐角, 所以,即. 亦即当时,直线是直线与的公垂线. 8. ∵为棱上一点,且, ∴, ∴. 要使平面,则要,且. ∵底面是矩形,底面,∴,,. ∵,∴, . ∵,∴.代入,解得. ∴存在实数,使平面.查看更多