2020版高考数学二轮复习 专题五 立体几何 专题对点练16 空间中的平行与几何体的体积 文

2020版高考数学二轮复习 专题五 立体几何 专题对点练16 空间中的平行与几何体的体积 文

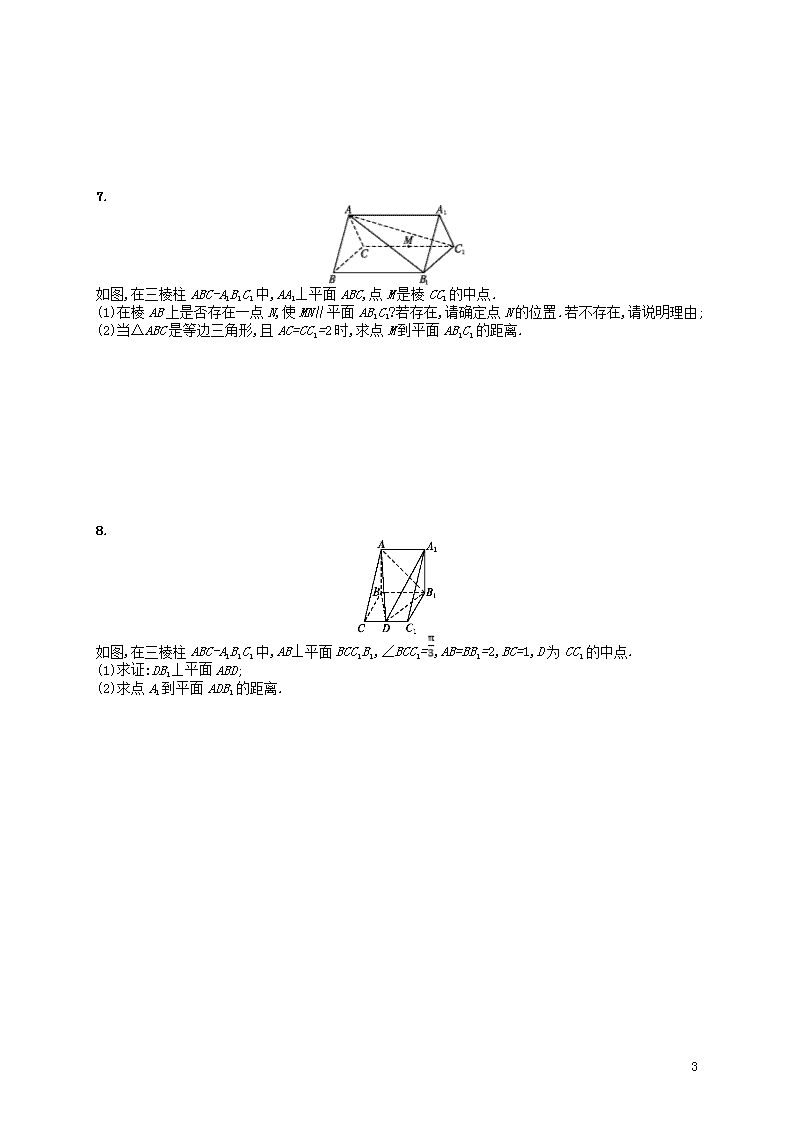
专题对点练16　空间中的平行与几何体的体积 ‎1.‎ 如图,已知斜三棱柱ABC-A1B‎1C1的所有棱长均为2,∠B1BA=,M,N分别为A‎1C1与B‎1C的中点,且侧面ABB‎1A1⊥底面ABC.‎ ‎(1)证明:MN∥平面ABB‎1A1;‎ ‎(2)求三棱柱B1-ABC的高及体积.‎ ‎2.(2018全国Ⅲ,文19)‎ 如图,矩形ABCD所在平面与半圆弧所在平面垂直,M是上异于C,D的点.‎ ‎(1)证明:平面AMD⊥平面BMC;‎ ‎(2)在线段AM上是否存在点P,使得MC∥平面PBD?说明理由.‎ ‎3.‎ ‎(2018广西名校联盟)如图,在三棱锥P-ABC中,AB⊥PC,CA=CB,M是AB的中点.点N在棱PC上,点D是BN的中点.‎ 求证:(1)MD∥平面PAC;‎ ‎(2)平面ABN⊥平面PMC.‎ 7‎ ‎4.‎ 如图,在四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是边长为2的等边三角形,E是BC的中点.‎ ‎(1)求证:AE∥平面PCD;‎ ‎(2)求四棱锥P-ABCD的体积.‎ ‎5.‎ 在三棱柱ABC-A1B‎1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,且D,E分别是棱A1B1,AA1的中点,点F在棱AB上,且AF=AB.‎ ‎(1)求证:EF∥平面BDC1;‎ ‎(2)求三棱锥D-BEC1的体积.‎ ‎6.‎ 如图,正方形ABCD的边长等于2,平面ABCD⊥平面ABEF,AF∥BE,BE=2AF=2,EF=.‎ ‎(1)求证:AC∥平面DEF;‎ ‎(2)求三棱锥C-DEF的体积.‎ 7‎ ‎7.‎ 如图,在三棱柱ABC-A1B‎1C1中,AA1⊥平面ABC,点M是棱CC1的中点.‎ ‎(1)在棱AB上是否存在一点N,使MN∥平面AB‎1C1?若存在,请确定点N的位置.若不存在,请说明理由;‎ ‎(2)当△ABC是等边三角形,且AC=CC1=2时,求点M到平面AB‎1C1的距离.‎ ‎8.‎ 如图,在三棱柱ABC-A1B‎1C1中,AB⊥平面BCC1B1,∠BCC1=,AB=BB1=2,BC=1,D为CC1的中点.‎ ‎(1)求证:DB1⊥平面ABD;‎ ‎(2)求点A1到平面ADB1的距离.‎ 7‎ 专题对点练16答案 ‎1.(1)证明 取AC的中点P,连接PN,PM.‎ ‎∵在斜三棱柱ABC-A1B‎1C1中,M,N分别为A‎1C1与B‎1C的中点,‎ ‎∴PN∥AB1,PM∥AA1.‎ ‎∵PM∩PN=P,AB1∩AA1=A,PM,PN⊂平面PMN,AB1,AA1⊂平面AB‎1A1,‎ ‎∴平面PMN∥平面AB‎1A1.‎ ‎∵MN⊂平面PMN,‎ ‎∴MN∥平面ABB‎1A1.‎ ‎(2)解 设O为AB的中点,连接B1O,由题意知△B1BA是正三角形,则B1O⊥AB.‎ ‎∵侧面ABB‎1A1⊥底面ABC,且交线为AB,∴B1O⊥平面ABC,‎ ‎∴三棱柱B1-ABC的高B1O=AB1=.‎ ‎∵S△ABC=×2×2×sin 60°=,‎ ‎∴三棱柱B1-ABC的体积V=S△ABC·B1O==1.‎ ‎2.解 (1)由题设知,平面CMD⊥平面ABCD,交线为CD.因为BC⊥CD,BC⊂平面ABCD,所以BC⊥平面CMD,故BC⊥DM.‎ 因为M为上异于C,D的点,且DC为直径,所以DM⊥CM.‎ 又BC∩CM=C,所以DM⊥平面BMC.‎ 而DM⊂平面AMD,‎ 故平面AMD⊥平面BMC.‎ ‎(2)当P为AM的中点时,MC∥平面PBD.‎ 证明如下:连接AC交BD于O.‎ 因为ABCD为矩形,所以O为AC中点.‎ 连接OP,因为P为AM中点,‎ 所以MC∥OP.‎ MC⊄平面PBD,OP⊂平面PBD,‎ 所以MC∥平面PBD.‎ ‎3.证明 (1)在△ABN中,M是AB的中点,D是BN的中点,‎ 所以MD∥AN.‎ 又因为AN⊂平面PAC,MD⊄平面PAC,所以MD∥平面PAC.‎ ‎(2)在△ABC中,CA=CB,M是AB的中点,‎ 所以AB⊥MC.‎ 又因为AB⊥PC,PC⊂平面PMC,MC⊂平面PMC,PC∩MC=C,所以AB⊥平面PMC.又因为AB⊂平面ABN,所以平面ABN⊥平面PMC.‎ ‎4.(1)证明 ∵∠ABC=∠BAD=90°,‎ ‎∴AD∥BC.‎ ‎∵BC=2AD,E是BC的中点,‎ ‎∴AD=CE,‎ ‎∴四边形ADCE是平行四边形,‎ 7‎ ‎∴AE∥CD.‎ 又AE⊄平面PCD,CD⊂平面PCD,‎ ‎∴AE∥平面PCD.‎ ‎(2)解 连接DE,BD,设AE∩BD=O,连接OP,‎ 则四边形ABED是正方形,‎ ‎∴O为BD的中点.‎ ‎∵△PAB与△PAD都是边长为2的等边三角形,∴BD=2,OB=,OA=,PA=PB=2,‎ ‎∴OP⊥OB,OP=,∴OP2+OA2=PA2,即OP⊥OA.‎ 又OA⊂平面ABCD,BD⊂平面ABCD,OA∩OB=O,∴OP⊥平面ABCD.‎ ‎∴VP-ABCD=S梯形ABCD·OP=×(2+4)×2×=2.‎ ‎5.(1)证明 取AB的中点O,连接A1O.‎ ‎∵AF=AB,∴F为AO的中点.‎ 又E为AA1的中点,∴EF∥A1O.‎ ‎∵A1D=A1B1,BO=AB,AB