- 2021-05-13 发布 |
- 37.5 KB |
- 5页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考数学二轮复习专题四第二讲点、直线、平面之间的位置关系理更多关注高中学习资料库
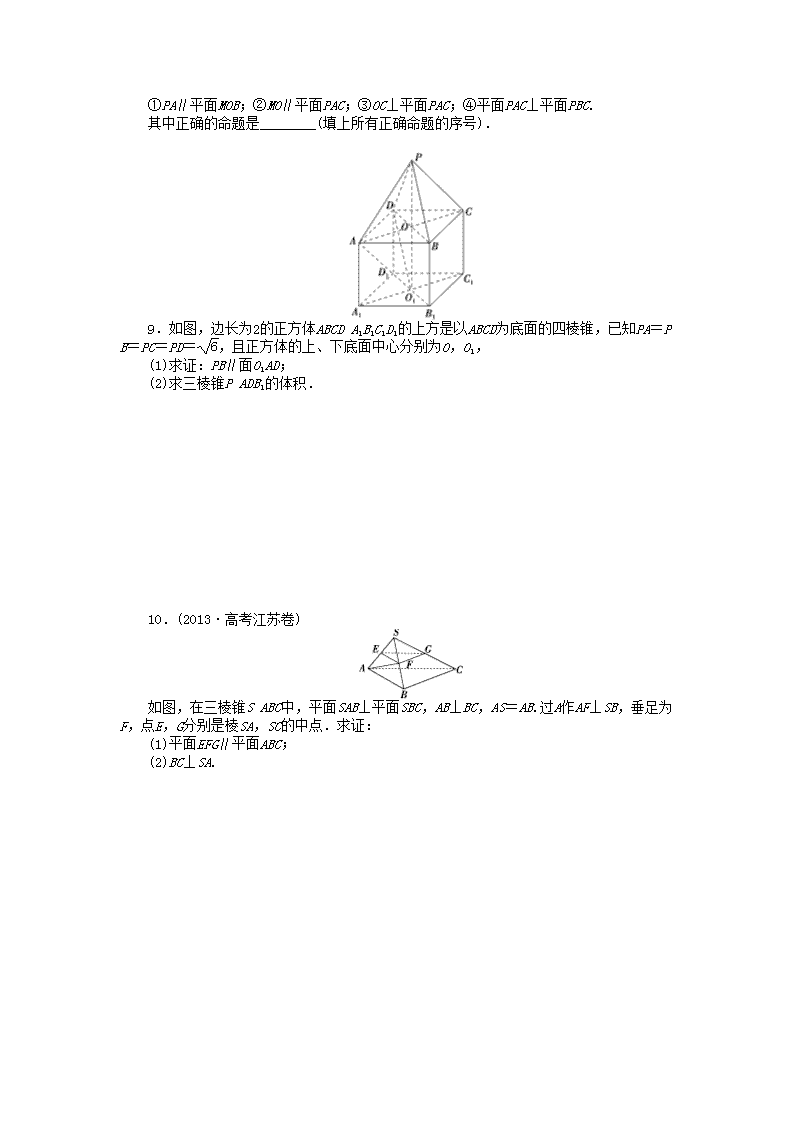
第二讲 点、直线、平面之间的位置关系 1.(2013·高考安徽卷)在下列命题中,不是公理的是( ) A.平行于同一个平面的两个平面相互平行 B.过不在同一条直线上的三点,有且只有一个平面 C.如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内 D.如果两个不重合的平面有一个公共点, 那么它们有且只有一条过该点的公共直线 2.(2013·内蒙古乌海检测)已知异面直线a,b分别在平面α,β内,且α∩β=c,那么直线c一定( ) A.与a,b都相交 B.只能与a,b中的一条相交 C.至少与a,b中的一条相交 D.与a,b都平行 3.(2013·高考广东卷)设l为直线,α,β是两个不同的平面.下列命题中正确的是( ) A.若l∥α,l∥β,则α∥β B.若l⊥α,l⊥β,则α∥β C.若l⊥α,l∥β,则α∥β D.若α⊥β,l∥α,则l⊥β 4.(2013·河北省质量检测)已知α、β是两个不同的平面,给出下列四个条件:①存在一条直线a,a⊥α,a⊥β;②存在一个平面γ,γ⊥α,γ⊥β;③存在两条平行直线a、b,a⊂α,b⊂β,a∥β,b∥α;④存在两条异面直线a、b,a⊂α,b⊂β,a∥β,b∥α,可以推出α∥β的是( ) A.①③ B.②④ C.①④ D.②③ 5.将图(1)中的等腰直角三角形ABC沿斜边BC的中线折起得到空间四面体ABCD(如图(2)),则在空间四面体ABCD中,AD与BC的位置关系是( ) A.相交且垂直 B.相交但不垂直 C.异面且垂直 D.异面但不垂直 6.(2013·武汉市武昌区联考)已知直线l⊥平面α,直线m⊂平面β,有下列命题: ①α∥β⇒l⊥m;②α⊥β⇒l∥m;③l∥m⇒α⊥β;④l⊥m⇒α∥β. 其中正确命题的序号是________. 7.(2013·广东省惠州市调研)已知m,n是两条不同直线,α,β,γ是三个不同平面,下列命题中正确的有________. ①若m∥α,n∥α,则m∥n;②若α⊥γ,β⊥γ,则α∥β; ③若m∥α,m∥β,则α∥β;④若m⊥α,n⊥α,则m∥n. 8. 如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M为线段PB的中点.有以下四个命题: ①PA∥平面MOB;②MO∥平面PAC;③OC⊥平面PAC;④平面PAC⊥平面PBC. 其中正确的命题是________(填上所有正确命题的序号). 9.如图,边长为2的正方体ABCDA1B1C1D1的上方是以ABCD为底面的四棱锥,已知PA=PB=PC=PD=,且正方体的上、下底面中心分别为O,O1, (1)求证:PB∥面O1AD; (2)求三棱锥PADB1的体积. 10.(2013·高考江苏卷) 如图,在三棱锥SABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB.过A作AF⊥SB,垂足为F,点E,G分别是棱SA,SC的中点.求证: (1)平面EFG∥平面ABC; (2)BC⊥SA. 11.如图,已知直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,BC=2,CD=1+,过A作AE⊥CD,垂足为E,G、F分别为AD、EC的中点,现将△ADE沿AE折起,使得DE⊥EC. (1)求证:BC⊥平面CDE; (2)求证:FG∥平面BCD; (3)在线段AE上找一点R,使得平面BDR⊥平面DCB,并说明理由. 答案: 1.【解析】选A.A,不是公理,是个常用的结论,需经过推理论证; B,是平面的基本性质公理; C,是平面的基本性质公理; D,是平面的基本性质公理. 2.【解析】选C.若c与a,b都不相交,则c与a,b都平行,根据公理4,知a∥b,与a,b异面矛盾.故选C. 3.【解析】选B.选项A,若l∥α,l∥β,则α和β可能平行也可能相交,故错误; 选项B,若l⊥α,l⊥β,则α∥β,故正确; 选项C,若l⊥α,l∥β,则α⊥β,故错误; 选项D,若α⊥β,l∥α,则l与β的位置关系有三种可能:l⊥β,l∥β,l⊂β,故错误.故选B. 4.【解析】选C.对于②,平面α与β还可以相交;对于③,当a∥b时,不一定能推出α∥β,所以②③是错误的,易知①④正确,故选C. 5.【解析】选C.在题图(1)中的等腰直角三角形ABC中,斜边上的中线AD就是斜边上的高,则AD⊥BC.翻折后如题图(2),AD与BC变成异面直线,而原线段BC变成两条线段BD、CD,这两条线段与AD垂直,即AD⊥BD,AD⊥CD,BD∩CD=D,故AD⊥平面BCD,所以AD⊥BC.故选C. 6.【解析】①正确,∵l⊥α,α∥β,∴l⊥β,又m⊂β,∴l⊥m;②错误,l,m也可以垂直,还可以异面;③正确,∵l⊥α,l∥m,∴m⊥α,又m⊂β,∴α⊥β;④错误,α与β可能相交. 【答案】①③ 7.【解析】若m∥α,n∥α,m,n可以平行,可以相交,也可以异面,故①不正确;若α⊥γ,β⊥γ,α,β可以相交,故②不正确;若m∥α,m∥β,α,β可以相交,故③不正确;若m⊥α,n⊥α,则m∥n,④正确.故填④. 【答案】④ 8.【解析】①错误,PA⊂平面MOB;②正确;③错误,否则,有OC⊥AC,这与BC⊥AC矛盾;④正确,因为BC⊥平面PAC. 【答案】②④ 9. 【解】(1)如图,作OE⊥BC于E,连结PE,则PE⊥BC,易得PE==,PO=2,连接OB1得四边形PBB1O为平行四边形,于是PB∥OB1, 又OB1∥DO1, ∴PB∥DO1, 又PB⊄平面O1AD, DO1⊂平面O1AD, ∴PB∥平面O1AD. (2)由于VPADB1=VAPDB1,易得三棱锥APDB1的高即为AO=AC=, S△PDB1=SDD1B1B+S△PDB-S△DD1B1-S△PB1B =2×2+×2×2-×2×2-×2×=3, 故三棱锥PADB1的体积为VPADB1=×3×=2. 10.【证明】(1)因为AS=AB,AF⊥SB, 垂足为F,所以F是SB的中点. 又因为E是SA的中点, 所以EF∥AB. 因为EF⊄平面ABC,AB⊂平面ABC, 所以EF∥平面ABC. 同理EG∥平面ABC.又EF∩EG=E, 所以平面EFG∥平面ABC. (2)因为平面SAB⊥平面SBC,且交线为SB, 又AF⊂平面SAB,AF⊥SB,所以AF⊥平面SBC. 因为BC⊂平面SBC,所以AF⊥BC. 又因为AB⊥BC,AF∩AB=A,AF⊂平面SAB,AB⊂平面SAB,所以BC⊥平面SAB. 因为SA⊂平面SAB,所以BC⊥SA. 11.【解】(1)由已知得DE⊥AE,DE⊥EC,∵AE∩EC=E,AE、EC⊂平面ABCE,∴DE⊥平面ABCE,∴DE⊥BC.又BC⊥EC,EC∩DE=E,∴BC⊥平面CDE. (2)取AB中点H,连接GH、FH,如图所示. ∴GH∥BD,FH∥BC, ∴GH∥平面BCD,FH∥平面BCD. ∴平面FHG∥平面BCD, ∴GF∥平面BCD. (3)R点满足3AR=RE时,平面BDR⊥平面DCB.取BD中点Q,连接DR、BR、CR、CQ、RQ,如图所示: 易得CD=2,BR=,CR=,DR=,CQ=, 在△BDR中,∵BR=,DR=,BD=2,可知RQ=, ∴在△CRQ中,CQ2+RQ2=CR2,∴CQ⊥RQ. 又在△CBD中,CD=DB,Q为BD的中点, ∴CQ⊥BD,∴CQ⊥平面BDR, ∴平面BDC⊥平面BDR.查看更多