高考极坐标与参数方程常见题型

高考极坐标与参数方程常见题型

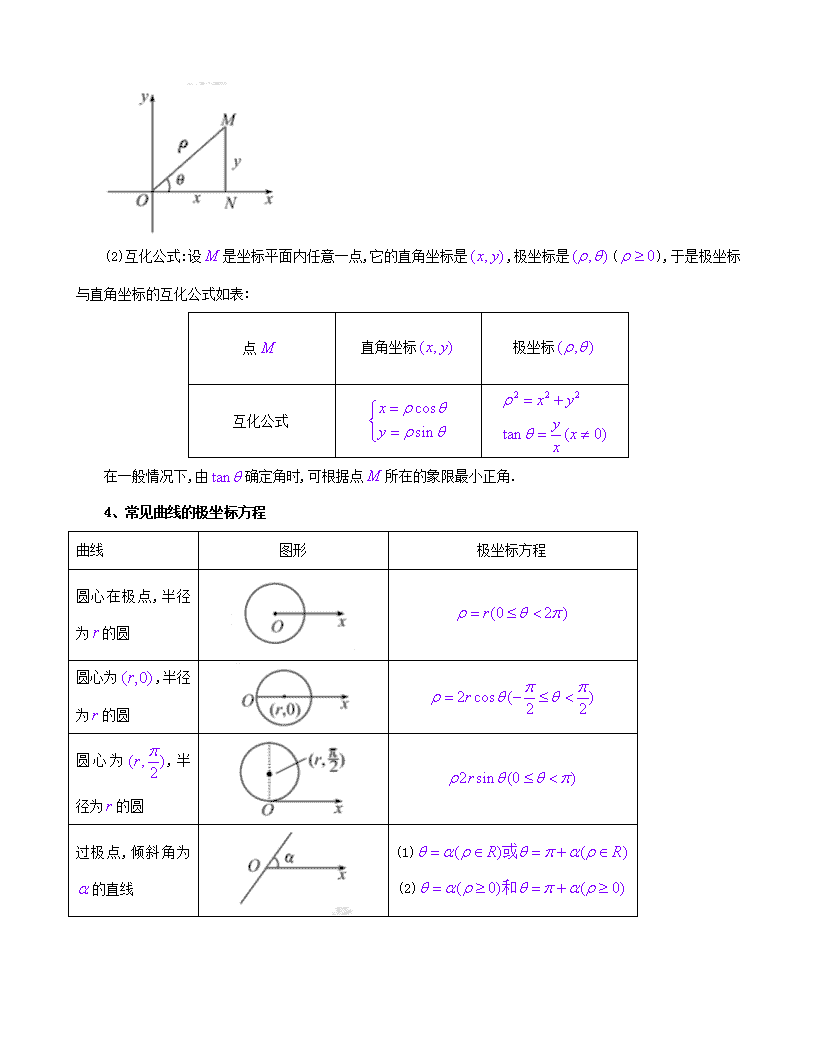
极坐标与参数方程 一、基础知识点梳理 ‎（一）极坐标 极坐标系的概念 ‎(1)极坐标系 如图所示,在平面内取一个定点,叫做极点,自极点引一条射线,叫做极轴;再选定一个长度单位,一个角度单位(通常取弧度)及其正方向(通常取逆时针方向),这样就建立了一个极坐标系.‎ 注:极坐标系以角这一平面图形为几何背景,而平面直角坐标系以互相垂直的两条数轴为几何背景;平面直角坐标系内的点与坐标能建立一一对应的关系,而极坐标系则不可.但极坐标系和平面直角坐标系都是平面坐标系.‎ ‎(2)极坐标 设M是平面内一点,极点与点M的距离|OM|叫做点M的极径,记为;以极轴为始边,射线为终边的角叫做点M的极角,记为.有序数对叫做点M的极坐标,记作.‎ 一般地,不作特殊说明时,我们认为可取任意实数.‎ 特别地,当点在极点时,它的极坐标为(0, )(∈R).和直角坐标不同,平面内一个点的极坐标有无数种表示.‎ 如果规定,那么除极点外,平面内的点可用唯一的极坐标表示;同时,极坐标表示的点也是唯一确定的.‎ ‎3、极坐标和直角坐标的互化 ‎(1)互化背景:把直角坐标系的原点作为极点,x轴的正半轴作为极轴,并在两种坐标系中取相同的长度单位,如图所示:‎ ‎(2)互化公式:设是坐标平面内任意一点,它的直角坐标是,极坐标是(),于是极坐标与直角坐标的互化公式如表:‎ 点 直角坐标 极坐标 互化公式 在一般情况下,由确定角时,可根据点所在的象限最小正角.‎ ‎4、常见曲线的极坐标方程 曲线 图形 极坐标方程 圆心在极点,半径为的圆 圆心为,半径为的圆 圆心为,半径为的圆 过极点,倾斜角为的直线 ‎(1)‎ ‎(2)‎ 过点,与极轴垂直的直线 过点,与极轴平行的直线 ‎（二）、参数方程 ‎1、参数方程的概念 一般地,在平面直角坐标系中,如果曲线上任意一点的坐标都是某个变数的函数①,并且对于的每一个允许值,由方程组①所确定的点都在这条曲线上,那么方程①就叫做这条曲线的参数方程,联系变数的变数叫做参变数,简称参数,相对于参数方程而言,直接给出点的坐标间关系的方程叫做普通方程.‎ ‎2、参数方程和普通方程的互化 ‎(1)曲线的参数方程和普通方程是曲线方程的不同形式,一般地可以通过消去参数而从参数方程得到普通方程.‎ ‎(2)如果知道变数中的一个与参数的关系,例如,把它代入普通方程,求出另一个变数与参数的关系,那么就是曲线的参数方程,在参数方程与普通方程的互化中,必须使的取值范围保持一致.‎ 注：普通方程化为参数方程，参数方程的形式不一定唯一。应用参数方程解轨迹问题，关键在于适当地设参数，如果选用的参数不同，那么所求得的曲线的参数方程的形式也不同。‎ ‎3、圆的参数 圆心为，半径为的圆的普通方程是，‎ 它的参数方程为：。‎ ‎4、椭圆的参数方程 以坐标原点为中心，焦点在轴上的椭圆的标准方程为其参数方程为，其中参数称为离心角；焦点在轴上的椭圆的标准方程是其参数方程为其中参数仍为离心角，通常规定参数的范围为∈[0，2）。‎ ‎5、双曲线的参数方程 以坐标原点为中心，焦点在轴上的双曲线的标准议程为其参数方程为，其中 焦点在轴上的双曲线的标准方程是其参数方程为 ‎ 二、极坐标与参数方程历年高考题：‎ ‎1、 在以O为极点的极坐标系中，圆ρ＝4sin θ和直线ρsin θ＝a相交于A，B两点．若△AOB是等边三角形，则a的值为________．‎ ‎2、 以平面直角坐标系的原点为极点，x轴的正半轴为极轴，建立极坐标系，两种坐标系中取相同的长度单位．已知直线l的参数方程是(t为参数)，圆C的极坐标方程是ρ＝4cos θ，则直线l被圆C截得的弦长为(　　)‎ A. B．2 C. D．2 ‎3、曲线(θ为参数)的对称中心(　　)‎ A．在直线y＝2x上 B．在直线y＝－2x上 C．在直线y＝x－1上 D．在直线y＝x＋1上 ‎4、在极坐标系中，点到直线ρsin＝1的距离是________．‎ ‎5、在极坐标系中，曲线C1和C2的方程分别为ρsin2θ＝cos θ和ρsin θ＝1.以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，则曲线C1和C2交点的直角坐标为________．‎ ‎6、已知曲线C1的参数方程是(t为参数)．以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程是ρ＝2，则C1与C2交点的直角坐标为________．‎ ‎7、在平面直角坐标系中，倾斜角为的直线l与曲线C：(α为参数)交于A，B两点，且|AB|＝2.以坐标原点O为极点，x轴正半轴为极轴建立极坐标系，则直线l的极坐标方程是________．‎ ‎　‎ ‎8、已知直线l的参数方程为(t为参数)，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρsin2θ－4cos θ＝0(ρ≥0，0≤θ<2π)，则直线l与曲线C的公共点的极径ρ＝________．‎ ‎9、在直角坐标系xOy中，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，半圆C的极坐标方程为ρ＝2cos θ，θ∈.‎ ‎(1)求C的参数方程；‎ ‎(2)设点D在C上，C在D处的切线与直线l：y＝x＋2垂直，根据(1)中你得到的参数方程，确定D的坐标．‎ ‎ 10、已知直线l的参数方程为(t为参数)，圆C的参数方程为(θ为参数)．‎ ‎(1)求直线l和圆C的普通方程；‎ ‎(2)若直线l与圆C有公共点，求实数a的取值范围．‎ ‎11、已知直线的参数方程为，（t为参数），圆的参数方程为，（θ为常数）．‎ ‎①求直线和圆的普通方程；‎ ‎②若直线与圆有公共点，求实数的取值范围．‎ ‎12、将圆上每一点的横坐标保持不变，纵坐标变为原来的2倍，得曲线C．‎ ‎⑴写出C的参数方程；‎ ‎⑵设直线l:2x+y-2=0与C的交点为以坐标原点为极点，x轴正半轴为极轴建立极坐标系，求过线段的中点且与垂直的直线的极坐标方程．‎ ‎13、已知曲线C：＋＝1，直线l：(t为参数)．‎ ‎(1)写出曲线C的参数方程，直线l的普通方程；‎ ‎(2)过曲线C上任意一点P作与l夹角为30°的直线，交l于点A，求|PA|的最大值与最小值．‎ ‎14、‎