- 2021-05-13 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
浙江高考数学试题文科含试卷详细答案
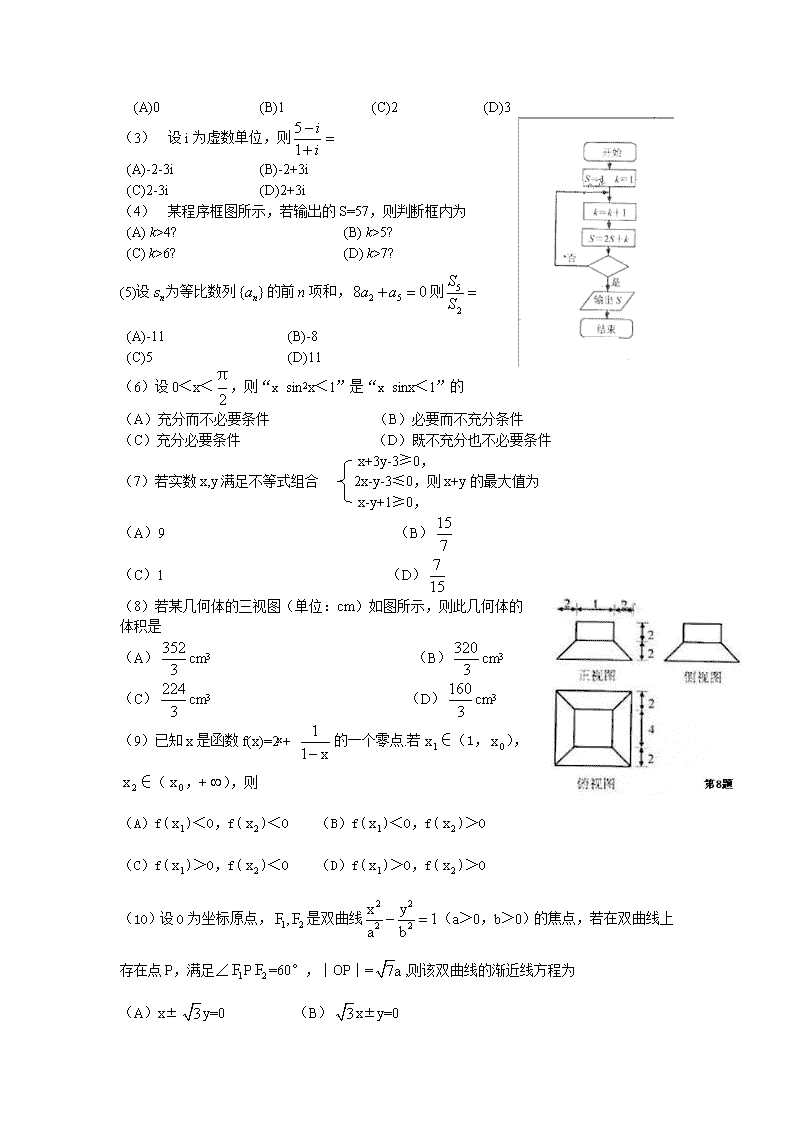
2010年普通高等学校招生全国统一考试(浙江卷) 数学试题(文科) 本试题卷分选择题和非选择题两部分。全卷共5页,选择题部分1至2页,非选择题部分3至5页。满分150分,考试时间120分钟。 请考生按规定用笔讲所有试题的答案涂、写在答题纸上。 选择题部分(共50分) 参考公式: 如果事件互斥,那么 柱体的体积公式 [ 如果事件相互独立,那么 其中表示柱体的底面积,表示柱体的高 锥体的体积公式 如果事件A在一次试验中发生的概率是, 那么次独立重复试验中事件恰好发生 其中表示锥体的底面积,表示锥体的高 次的概率 球的表面积公式 台体的体积公式 球的体积公式 其中分别表示台体的上、下底面积, 表示台体的高 其中R表示球的半径 一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的。 (1) 设则 (A) (B) (C) (D) (2) 已知函数 若 = (A)0 (B)1 (C)2 (D)3 (1) 设i为虚数单位,则 (A)-2-3i (B)-2+3i (C)2-3i (D)2+3i (2) 某程序框图所示,若输出的S=57,则判断框内为 (A) k>4? (B) k>5? (C) k>6? (D) k>7? (5)设为等比数列的前n项和,则 (A)-11 (B)-8 (C)5 (D)11 (6)设0<x<,则“x sin2x<1”是“x sinx<1”的 (A)充分而不必要条件 (B)必要而不充分条件 (C)充分必要条件 (D)既不充分也不必要条件 x+3y-3≥0, (7)若实数x,y满足不等式组合 2x-y-3≤0,则x+y的最大值为 x-y+1≥0, (A)9 (B) (C)1 (D) (8)若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是 (A)cm3 (B)cm3 (C)cm3 (D)cm3 (9)已知x是函数f(x)=2x+ 的一个零点.若∈(1,), ∈(,+),则 (A)f()<0,f()<0 (B)f()<0,f()>0 (C)f()>0,f()<0 (D)f()>0,f()>0 (10)设O为坐标原点,,是双曲线(a>0,b>0)的焦点,若在双曲线上存在点P,满足∠P=60°,∣OP∣=,则该双曲线的渐近线方程为 (A)x±y=0 (B)x±y=0 (C)x±=0 (D)±y=0 非选择题部分(共100分) 二,填空题:本大题共7小题,每小题4分,共28分。 (11)在如图所示的茎叶图中,甲、乙两组数据的中位数分别是 、 (12)函数的最小正周期是 。 (13)已知平面向量则的值是 。 (14)在如下数表中,已知每行、每列中的树都成等差数列, 那么,位于下表中的第n行第n+1列的数是 。 (15)若正实数X,Y 满足2X+Y+6=XY , 则XY 的最小值是 。 (16) 某商家一月份至五月份累计销售额达3860万元,预测六月份销售额为500万元,七月份销售额比六月份递增x%,八月份销售额比七月份递增x%,九、十月份销售总额与七、八月份销售总额相等,若一月至十月份销售总额至少至少达7000万元,则,x 的最小值 。 (17)在平行四边形ABCD中,O是AC与BD的交点,P、Q、M、N分别是线段OA、OB、OC、OD的中点,在APMC中任取一点记为E,在B、Q、N、D中任取一点记为F,设G为满足向量的点,则在上述的点G组成的集合中的点,落在平行四边形ABCD外(不含边界)的概率为 。 三、解答题:本大题共5小题,共72分。解答应写出文字说明、证明过程或演算步骤。 (18)(本题满分)在△ABC中,角A,B,C所对的边分别为a,b,c,设S为△ABC的面积,满足。 (Ⅰ)求角C的大小; (Ⅱ)求的最大值。 (19)(本题满分14分)设a1,d为实数,首项为a1,公差为d的等差数列{an}的前n项和为Sn,满足+15=0。 (Ⅰ)若=5,求及a1; (Ⅱ)求d的取值范围。 (20)(本题满分14分)如图,在平行四边形ABCD中,AB=2BC,∠ABC=120°。E为线段AB的中点,将△ADE沿直线DE翻折成△A’DE,使平面A’DE⊥平面BCD,F为线段A’C的中点。 (Ⅰ)求证:BF∥平面A’DE; (Ⅱ)设M为线段DE的中点,求直线FM与平面A’DE所成角的余弦值。 (21)(本题满分15分)已知函数(a-b)查看更多