高考物理二轮复习曲线运动教案

高考物理二轮复习曲线运动教案

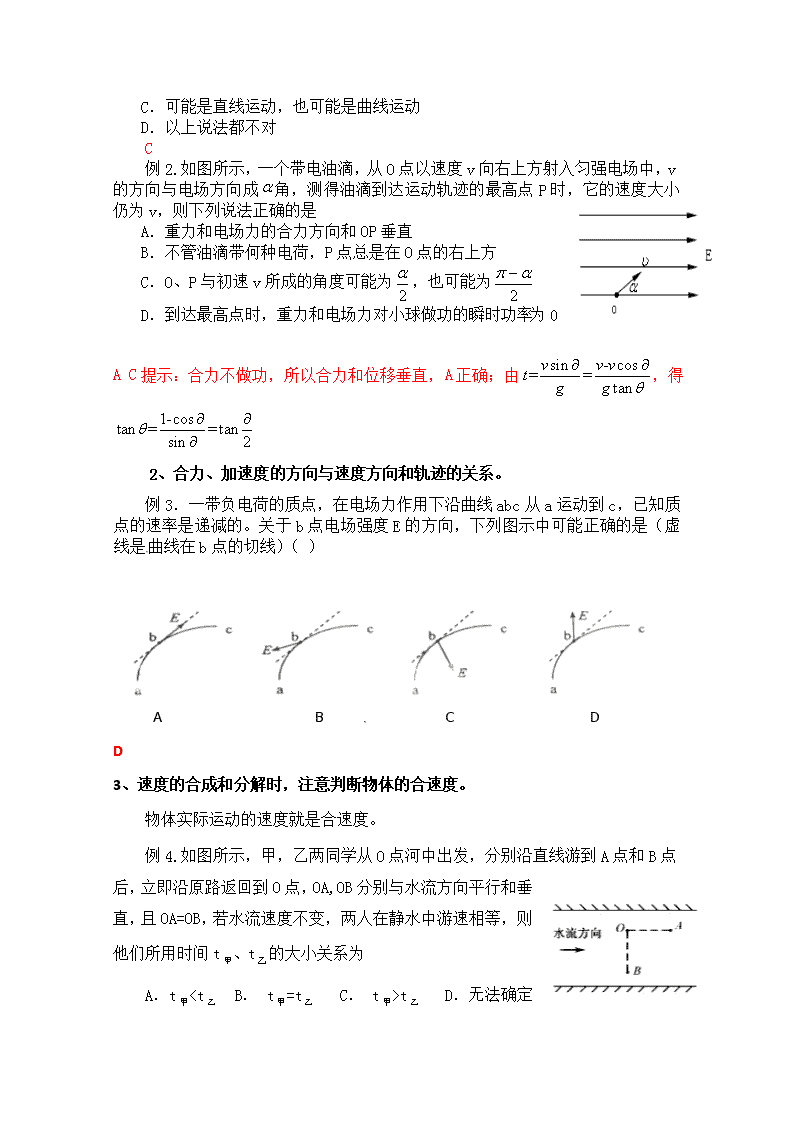
第四章 曲线运动 网络知识 曲线运动 ‎ 圆周运动 匀速圆周运动 线速度v=, 角速度ω=‎ 向心加速度 向心力 变速圆周运动 一般变速运动:向心力沿半径方向 竖直平面内的圆周运动过最高点的临界条件:‎ ‎（绳）‎ ‎（杆）‎ 平抛物体的运动 运动规律 位移 速度 动力学分析 力 ay=g ax=0‎ 加速度 Vy=gt 产生条件：速度与力不在同一条直线上 研究方法：运动的合成与分解 ‎：‎ ‎[来源:学科网]‎ 特例 周期 一、曲线运动规律应用应注意的问题：‎ ‎1、曲线运动的一般研究方法 例1.关于互成角度的两个初速度不为零的匀变速直线运动的合运动，下列说法正确的是 A． 一定是直线运动 ‎ B． 一定是抛物线运动 ‎ C．可能是直线运动，也可能是曲线运动 ‎ ‎ D．以上说法都不对 C 例2.如图所示，一个带电油滴，从O点以速度v向右上方射入匀强电场中，v的方向与电场方向成角，测得油滴到达运动轨迹的最高点P时，它的速度大小仍为v，则下列说法正确的是 [来源:学#科#网Z#X#X#K]‎ ‎ A．重力和电场力的合力方向和OP垂直 ‎ B．不管油滴带何种电荷，P点总是在O点的右上方 ‎ C．O、P与初速v所成的角度可能为，也可能为 ‎ D．到达最高点时，重力和电场力对小球做功的瞬时功率为0[来源:学#科#网]‎ A C提示：合力不做功，所以合力和位移垂直，A正确；由，得 ‎ 2、合力、加速度的方向与速度方向和轨迹的关系。‎ 例3．一带负电荷的质点，在电场力作用下沿曲线abc从a运动到c，已知质点的速率是递减的。关于b点电场强度E的方向，下列图示中可能正确的是（虚线是曲线在b点的切线）（ ）‎ A B C D D ‎3、速度的合成和分解时，注意判断物体的合速度。‎ ‎ 物体实际运动的速度就是合速度。‎ 例4.如图所示，甲，乙两同学从O点河中出发，分别沿直线游到A点和B点后，立即沿原路返回到O点，OA,OB分别与水流方向平行和垂直，且OA=OB，若水流速度不变，两人在静水中游速相等，则他们所用时间t、t的大小关系为 A．tt D．无法确定 提示 : C ‎ ‎4、连带运动中的牵连速度问题 ‎ （1）物体运动速度与绳（杆）不共线时，存在牵连速度问题。‎ ‎（2）不可伸长的绳（杆）尽管各点的速度不同，但各点速度沿绳（杆）方向的投影相同。‎ 例5、如图，一半圆形碗的边缘上装有一定滑轮，滑轮两边通过一不可伸长的轻质细线挂着两个小物体，质量分别为m1、m2, m1＞m2。现让m1从靠近定滑轮处由静止开始沿碗内壁下滑。设碗固定不动，其内壁光滑、半径为R。则m1滑到碗最低点时的速度为：（ ）‎ ‎ A B ‎ C D ‎ A 例6．如图，人沿平直的河岸以速度行走，且通过不可伸长的绳拖船，船沿绳的方向行进，此过程中绳始终与水面平行。当绳与河岸的夹角为，船的速率为 A． B． ‎ C． D． ‎ C ‎5、研究平抛问题的常用方法：‎ ‎（1）分解位移： ‎ a b c x y O 例7.（12新课标）15.如图，x轴在水平地面内，y轴沿竖直方向。图中画出了从y轴上沿x轴正向抛出的三个小球a、b和c的运动轨迹，其中b和c是从同一点抛出的，不计空气阻力，则 A.a的飞行时间比b的长 B.b和c的飞行时间相同 C.a的水平速度比b的小 D.b的初速度比c的大 BD 例8.（12高考上海）如图，斜面上a、b、c三点等距，小球从a点正上方O点抛出，做初速为v0的平抛运动，恰落在b点。若小球初速变为v，其落点位于c，则 （ ）‎ ‎（A）v0< v <2v0 （B）v=2v0‎ ‎（C）2v0< v <3v0 （D）v>3v0‎ A ‎（2）分解速度： ‎ ‎（3）分解加速度：‎ 例9.如图所示，从倾角为θ的斜坡顶端以初速度v0水平抛出一小球，不计空气阻力，设斜坡足够长，则小球抛山后离开斜坡的最大距离H是多少?‎ 答案:[来源:Zxxk.Com]‎ ‎（4）速度偏向角的正切值tanα等于位移偏向角正切值tanθ的2倍。[来源:Z+xx+k.Com]‎ 即：tanα=2tanθ，‎ 例10．一水平抛出的小球落到一倾角为的斜面上时，其速度方向与斜面垂直，运动轨迹如右图中虚线所示。小球在竖直方向下落的距离与在水平方向通过的距离之比为 A．　　　　　　　　　　 B．‎ C．　　　　　　　　　　D．‎ D ‎6、类平抛运动的研究：‎ 受到与初速方向垂直的恒力作用时，物体的运动可借鉴平抛运动的研究方法研究。‎ ‎ ‎ 例11.如图所示，光滑斜面长为b，宽为a，倾角为θ，一物块沿斜面左上方顶点P水平射出，恰从右下方顶点Q离开斜面，问入射初速度v0应多大?‎ 答案:‎ ‎7、匀速圆周运动：‎ F=man , an = = =‎ ‎（1）水平面内的匀速圆周运动 例12、如图所示，一圆盘可以绕其竖直轴在水平面内运动，圆盘半径为R，甲、乙两物体的质量分别为M和m(M>m)，它们与圆盘之间的最大静摩擦力均为正压力的μ倍，两物体用长为L的轻绳连在一起，L

查看更多