高考数学理二轮专练六仿真模拟题目二
仿真模拟题(二)
一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知全集U=R,集合A={0,1,2,3,4,5},B={x∈R|x≥2},则图中阴影部分所表示的集合为( )
A.{0,1} B.{1}
C.{1,2} D.{0,1,2}
2.已知函数f(x)=,则f(f())的值是( )
A.9 B.
C.-9 D.-
3.从某中学甲、乙两个班中各随机抽取10名同学,测量他们的身高(单位:cm)后获得身高数据的茎叶图如图1,在这20人中,记身高在[150,160),[160,170),[170,180),[180,190)的人数依次为A1,A2,A3,A4,图2是统计样本中身高在一定范围内的人数的程序框图,则下列说法正确的是( )
A.由图1可知甲、乙两班中平均身高较高的是甲班,图2输出的S的值为18
B.由图1可知甲、乙两班中平均身高较高的是乙班,图2输出的S的值为16
C.由图1可知甲、乙两班中平均身高较高的是乙班,图2输出的S的值为18
D.由图1可知甲、乙两班中平均身高较高的是甲班,图2输出的S的值为16
4.(2013·福建省普通高中毕业班质量检测)已知F1,F2是椭圆C的两个焦点,焦距为4.若P为椭圆C上一点,且△PF1F2的周长为14,则椭圆C的离心率e为( )
A. B.
C. D.
5.在函数y=f(x)的图象上有点列(xn,yn),若数列{xn}是等差数列,数列{yn}是等比数列,则函数y=f(x)的解析式可能为( )
A.f(x)=2x+1 B.f(x)=4x2
C.f(x)=log3x D.f(x)=()x
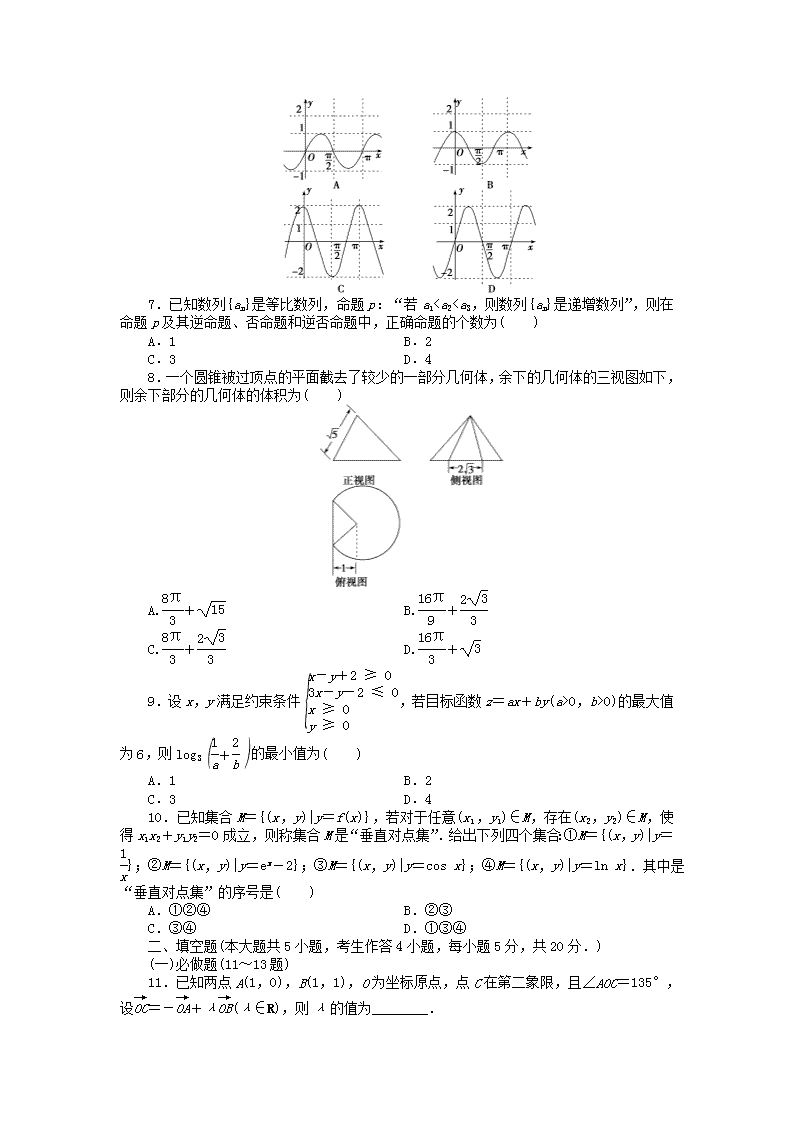
6.(2013·云南省昆明市高三调研测试)已知a是实数,则函数f(x)=acos ax的图象可能是( )
7.已知数列{an}是等比数列,命题p:“若a1
0,b>0)的最大值为6,则log3的最小值为( )
A.1 B.2
C.3 D.4
10.已知集合M={(x,y)|y=f(x)},若对于任意(x1,y1)∈M,存在(x2,y2)∈M,使得x1x2+y1y2=0成立,则称集合M是“垂直对点集”.给出下列四个集合:①M={(x,y)|y=};②M={(x,y)|y=ex-2};③M={(x,y)|y=cos x};④M={(x,y)|y=ln x}.其中是“垂直对点集”的序号是( )
A.①②④ B.②③
C.③④ D.①③④
二、填空题(本大题共5小题,考生作答4小题,每小题5分,共20分.)
(一)必做题(11~13题)
11.已知两点A(1,0),B(1,1),O为坐标原点,点C在第二象限,且∠AOC=135°,设=-+λ(λ∈R),则λ的值为________.
12.如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=BD,BC=2BD,则sin C的值为________.
13.已知△ABC的顶点A,B分别是离心率为e的圆锥曲线+=1的焦点,顶点C在该曲线上;一同学已正确地推得:当m>n>0时有e(sin A+sin B)=sin C.类似地,当m>0,n<0时,有________.
(二)选做题(14~15题,考生只能从中选做一题)
14.(坐标系与参数方程选做题)已知直线3ρcos θ+4ρsin θ+a=0与曲线(θ为参数)有且仅有一个公共点,则正实数a的值为________.
15.(几何证明选讲选做题)如图,M是平行四边形四边形ABCD边AB的中点,直线l过M分别交AD、AC于E,F,交CB的延长线于N,若AE=2,AD=6,则AF∶AC的值为________.
三、解答题(本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤)
16.(本小题满分12分)在△ABC中,内角A,B,C对边分别是a,b,c,已知c=1,C=.
(1)若cos(α+C)=-,0<α<,求cos α;
(2)若sin C+sin(A-B)=3sin 2B,求△ABC的面积.
17.(本小题满分12分)某市的教育研究机构对全市高三学生进行综合素质测试,随机抽取了部分学生的成绩,得到如图所示的成绩频率分布直方图.
(1)估计全市学生综合素质成绩的平均值;
(2)若综合素质成绩排名前5名中,其中1人为某校的学生会主席,从这5人中推荐3
人参加自主招生考试.试求这3人中含该学生会主席的概率.
18.(本小题满分14分)(2013·高考山东卷)某几何体ABCA1B1C1的三视图和直观图如图所示.
(1)求证:平面AB1C1⊥平面AA1C1C;
(2)若E是线段AB1上的一点,且满足VEAA1C1=VABCA1B1C1,求AE的长.
19.(本小题满分14分)已知函数f(x)=·ex-f(0)·x+x2(e是自然对数的底数).
(1)求函数f(x)的解析式和单调区间;
(2)若函数g(x)=x2+a与函数f(x)的图象在区间[-1,2]上恰有两个不同的交点,求实数a的取值范围.
20.(本小题满分14分)(2013·高考广东卷)设各项均为正数的数列{an}的前 n项和为Sn,满足4Sn=a-4n-1,n∈N*,且a2,a5,a14构成等比数列.
(1)证明:a2=;
(2)求数列{an}的通项公式;
(3)证明:对一切正整数n,有++…+<.
21.(本小题满分14分)已知椭圆C:+=1(a>b>0)的离心率为,其左、右焦点分别为F1、F2,点P是坐标平面内一点,且||=,·=,其中O为坐标原点.
(1)求椭圆C的方程;
(2)如图,过点S(0,-),且斜率为k的动直线l交椭圆于A、B两点,在y轴上是否存在定点M,使以AB为直径的圆恒过这个定点?若存在,求出点M的坐标;若不存在,请说明理由.
答案:
1.【解析】选A.因为A∩B={2,3,4,5},图中阴影部分为A去掉A∩B,所以阴影部分所表示的集合为{0,1},所以选A.
2.【解析】选B.f()=log2=log22-2=-2,f(f())
=f(-2)=3-2=.
3.【解析】选C.由茎叶图可知,甲班学生身高的平均数为170.3,乙班学生身高的平均数为170.8,故乙班学生的平均身高较高.由题意可知,A1=2,A2=7,A3=9,A4=2,由程序框图易知,最后输出的结果为S=7+9+2=18.
4.【解析】选B.因为椭圆C的焦距为4,所以c=2.因为△PF1F2的周长为14,所以2a=14-4=10,所以a=5,所以椭圆C的离心率e==.
5.【解析】选D.对于函数f(x)=()x上的点列(xn,yn),有yn=()xn,由于{xn}是等差数列,设xn+1-xn=d,因此==()xn+1-xn=()d,这是一个与n无关的常数,故{yn}是等比数列.
6.【解析】选C.对于A、D,注意到当x=0时,f(x)=acos 0=a≠0,因此结合选项知,选项A、D不正确;对于B,注意到其最小正周期T==π,a=2,此时相应的最大值是2,这与所给的图象不相吻合,因此选项B不正确.综上所述,选C.
7.【解析】选D.若已知a10时,解得q>1,此时数列{an}是递增数列;当a1<0时,解得00,b>0)过直线x-y+2=0和3x-y-2=0的交点A(2,4)时,z取得最大值6,所以2a+4b=6,即a+2b=3,所以log3(+)=log3(+)·()=log3(++)≥log33=1,当且仅当a=b=1时取等号,故选A.
10.【解析】选B.对于①y=是以x,y轴为渐近线的双曲线,渐近线的夹角为90°,在同一支上,任意(x1,y1)∈M,不存在(x2,y2)∈M,满足垂直对点集的定义;对任意(x1,y1)∈M,在另一支上也不存在(x2,y2)∈M,使得x1x2+y1y2=0成立,所以不满足垂直对点集的定义,不是垂直对点集.
对于②M={(x,y)|y=ex-2},如图(1)在曲线上两点构成的直角存在,例如取M(0,-1),N(ln 2,0),满足垂直对点集的定义,所以正确.
对于③M={(x,y)|y=cos x},如图(2)对于任意(x1,y1)∈M,存在(x2,y2)∈M,使得x1x2+y1y2=0成立,
例如(0,1)、(,0),∠yOx=90°,满足垂直对点集的定义,旋转90°,都能在图象上找到满足题意的点,
所以集合M是垂直对点集;
对于④M={(x,y)|y=ln x},如图(3)取点(1,0),曲线上不存在另外的点,使得两点与原点的连线互相垂直,所以不是垂直对点集.故选B.
11.【解析】由∠AOC=135°知,点C在射线y=-x(x<0)上,设点C的坐标为(a,-a),则有(a,-a)=(-1+λ,λ),得a=-1+λ,-a=λ,消掉a得λ=.
【答案】
12.【解析】设AB=c,则AD=c,BD=,BC=,在△ABD中,由余弦定理得cos A==,则sin A=.在△ABC中,由正弦定理得==,解得sin C=.
【答案】
13.【解析】当m>n>0时,+=1为椭圆,
|AC|+|BC|=2,
由正弦定理知,==⇒=⇒=⇒e==⇒e(sin A+sin B)=sin C.当m>0,n<0时,+
=1为双曲线,||AC|-|BC||=2,由正弦定理知,==⇒=⇒=⇒e==⇒e|sin A-sin B|=sin C.
【答案】e|sin A-sin B|=sin C
14.【解析】由消参数得普通方程为:(x-1)2+y2=1,
直线3ρcos θ+4ρsin θ+a=0的直角坐标方程为:3x+4y+a=0,又圆与直线相切,所以=1,解得:a=2或a=-8(舍).
【答案】a=2
15.【解析】因为AD∥BC,
=⇒=,
∵==1⇒AE=BN,
∴==.
∵AE=2,AD=6,
∴==.即AF∶AC=1∶5.
【答案】1∶5
16.【解析】(1)∵cos(α+)=-,<α+<π,
∴sin(α+)==,
∴cos α=cos[(α+)-]=.
(2)∵sin(A+B)+sin(A-B)=2sin Acos B=6sin Bcos B,
∴cos B=0或sin A=3sin B,∴B=或a=3b.
若B=,则s=c·ctan A=;
若a=3b,由余弦定理得a2+b2-ab=1,b2=,
∴△ABC的面积S=absin C=.
17.【解】(1)依题意可知,
55×0.12+65×0.18+75×0.40+85×0.22+95×0.08=74.6,
所以全市学生综合素质成绩的平均值为74.6.
(2)设这5名学生分别为a,b,c,d,e,其中某校的学生会主席为a.从5人中选出3人,所有的可能的结果为(a,b,c),(a,b,d),(a,b,e),(a,c,d),(a,c,e),(a,d,e),(b,c,d),(b,c,e),(b,d,e),(c,d,e),共10种.
其中含有学生会主席的情况有(a,b,c),(a,b,d),(a,b,e),(a,c,d),(a,c,e),(a,d,e),共6种,故这3人中含该学生会主席的概率为=.
18.【解】(1)证明:由三视图可知,几何体ABCA1B1C1为三棱柱,侧棱AA1⊥底面A1B1C1,B1C1⊥A1C1,且AA1=AC=4,BC=2.
∵AA1⊥平面A1B1C1,B1C1⊂平面A1B1C1,
∴AA1⊥B1C1,
∵B1C1⊥A1C1,AA1∩A1C1=A1,
∴B1C1⊥平面A1ACC1.
又B1C1⊂平面AB1C1,∴平面AB1C1⊥平面AA1C1C.
(2)过点E作EF∥B1C1交AC1于点F(图略),
由(1)知,EF⊥平面A1ACC1,
即EF为三棱锥EAA1C1的高.
∵VEAA1C1=VABCA1B1C1,
∴S△AA1C1·EF=S△ABC·AA1,
∴×(×4×4)×EF=×(×2×4)×4,
解得EF=.
在Rt△ABC中,
AB===2,
在Rt△ABB1中,
AB1===6,
由=,得AE===2.
19.【解】(1)由已知得f′(x)=ex-f(0)+x,
∴f′(1)=f′(1)-f(0)+1,即f(0)=1.
又f(0)=,∴f′(1)=e.
从而f(x)=ex-x+x2.
显然f′(x)=ex-1+x在R上单调递增且f′(0)=0,
故当x∈(-∞,0)时,f′(x)<0;
当x∈(0,+∞)时,f′(x)>0.
∴f(x)的单调递减区间是(-∞,0),单调递增区间是(0,+∞).
(2)由f(x)=g(x)得a=ex-x.令h(x)=ex-x,
则h′(x)=ex-1.
由h′(x)=0得x=0.
当x∈(-1,0)时,h′(x)<0;当x∈(0,2)时,h′(x)>0.
∴h(x)在(-1,0)上单调递减,在(0,2)上单调递增.
又h(0)=1,h(-1)=1+,
h(2)=e2-2且h(-1)0,所以a2=.
(2)因为4Sn=a-4n-1,①
所以当n≥2时,4Sn-1=a-4(n-1)-1,②
由①-②得4an=a-a-4,
即a=a+4an+4=(an+2)2(n≥2).
因为an>0,所以an+1=an+2,即an+1-an=2(n≥2).
因为a2,a5,a14成等比数列,所以a=a2a14,
即(a2+3×2)2=a2(a2+12×2),解得a2=3.
又由(1)知a2=,所以a1=1,所以a2-a1=2.
综上知an+1-an=2(n∈N*),
所以数列{an}是首项为1,公差为2的等差数列.
所以an=1+2(n-1)=2n-1.
所以数列{an}的通项公式为an=2n-1(n∈N*).
(3)证明:由(2)知=
=,
所以++…+
=
==-<.
21.【解】(1)设P(x0,y0),则||=,
可知x+y=.①
∵·=,
∴(-c-x0,-y0)·(c-x0,-y0)=,
即x-c2+y=.②
将①代入②得,c=1,又e=,
可得a=,b=1,∴所求椭圆方程为+y2=1.
(2)存在点M(0,1)使以AB为直径的圆恒过该定点.
设直线l:y=kx-,代入+y2=1,
有(2k2+1)x2-kx-=0.
设A(x1,y1)、B(x2,y2),
则x1+x2=,x1x2=.
若y轴上存在定点M(0,m)满足题设,
则=(x1,y1-m),=(x2,y2-m),
·=x1x2+(y1-m)(y2-m)
=x1x2+y1y2-m(y1+y2)+m2
=x1x2+(kx1-)(kx2-)-m(kx1-+kx2-)+m2
=(k2+1)x1x2-k(+m)(x1+x2)+m2++
=.
由题意知,对任意实数k都有·=0恒成立,
即18(m2-1)k2+(9m2+6m-15)=0对k∈R成立.
∴,解得m=1,
∴在y轴上存在定点M(0,1),使以AB为直径的圆恒过这个定点.