- 2021-05-13 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考数学分专题训练函数yAsinwx a的图像
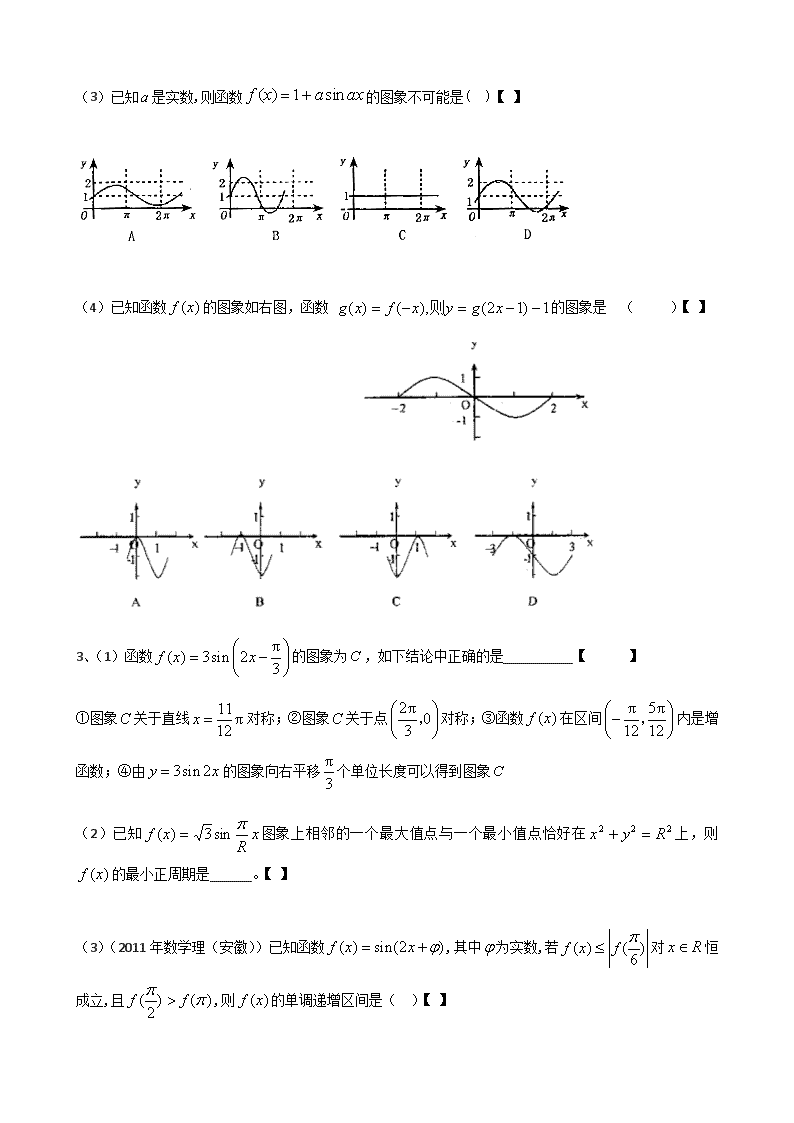
函数的图象 (一)基本知识点 1、图象的画法:(1)“五点法”;(2)图象变换法 2、由的图象求其函数式 Ø 3、的性质 Ø (二)经典例题: 1、(1)方程在区间上有两个不同的解,则实数的取值范围是______.【】 (2)已知函数. ①求函数的最小正周期;【】 ②用五点作图法作出函数在一个周期内的函数图象; ③求函数在区间上的最小值和最大值. 【最大值为,最小值为】 2、(1)若想将函数的图象进行平移,得到函数的图象,下面可行的变换步骤是 ( ) 【D】 A. 向左平移个单位 B. 向右平移个单位 C. 向左平移个单位 D. 向右平移个单位 (2)定义行列式运算:,将函数向左平移个单位,所得图象对应的函数则为偶函数,则的最小值是 ( )【B】 A. B.1 C. D.2 (3)已知是实数,则函数的图象不可能是( )【D】 (4)已知函数的图象如右图,函数 的图象是 ( )【C】 3、(1)函数的图象为,如下结论中正确的是__________【①②③】 ①图象关于直线对称;②图象关于点对称;③函数在区间内是增函数;④由的图象向右平移个单位长度可以得到图象 (2)已知图象上相邻的一个最大值点与一个最小值点恰好在上,则的最小正周期是______。【4】 (3)(2011年数学理(安徽))已知函数,其中为实数,若对恒成立,且,则的单调递增区间是( )【C】 (A) (B) (C) (D) (4)已知函数的最大值为3,图象经过点,且其相邻两对称轴间的距离为2,则.【200】 (5)数列中,,则=__________;若有一个形如的通项公式,其中均为实数,且,则此通项公式为=______(要求写出的数值)【2, 】 4、求下列函数的单调区间: (1) ;【增区间:】 (2);【增区间:】 (3)【增区间:】 图 5、(1)已知函数在一个周期内的图象如图所示,求直线y=与函数f(x)图象的所有交点的坐标。 【】 (2)(2009辽宁理)已知函数=Acos()的图象如图所示,,则= ( )【B】 (A) (B) (C)- (D) w.w.w.k.s.5.u.c.o.m (3)如图,是函数在同一个周期内的图像。 (I)求函数的解析式;【】 (II)将函数平移,得到函数的最大值,并求此时自变量的集合。【】 6、设的周期,最大值, (1)求、、的值;【】 (2)终边不共线,求的值。【】 7、(2010山东理)已知函数,其图像过点。 (1)求的值;【】 (2)将函数的图像上各点的横坐标缩短到原来的,纵坐标不变,等到函数的图像,求函数在上的最大值和最小值。【】 8、(2010江西理)已知函数。 (1) 当时,求在区间上的取值范围;【】 (2) 当时,,求的值。【】 9、(2011年数学文(重庆))设函数 (1)求的最小正周期;【】 (2)若函数的图象按平移后得到函数的图象,求在上的最大值.【】 10、若函数的图像与直线相切,并且切点的横坐标依次成公差为的等差数列。 (1)求的值;【】 (2)若点是图像的对称中心,且,求的坐标。【】 11、设函数的图象与直线,及轴所围成图形的面积称为函数在上的面积,已知函数在[0,]上的面积为(n∈N*),则 (1)函数在[0,]上的面积为_______;【】 (2)函数在[,]上的面积为______.【】 (三)巩固与提高: 1、(2010全国卷2理)为了得到函数的图像,只需把函数的图像( )【B】 (A)向左平移个长度单位 (B)向右平移个长度单位 (C)向左平移个长度单位 (D)向右平移个长度单位 2、求函数的对称轴方程。【】 3、若对任意实数都有,且,则实数m=_____。【】 4、(2011年数学理(全国新课标))设函数 的最小正周期为,且则( )【A】 (A)在单调递减 (B)在单调递减 (C)在单调递增 (D)在单调递增 5、把曲线ycosx+2y-1=0先沿x轴向右平移个单位,再沿y轴向下平移1个单位,得到的曲线方程是( )【C】 A.(1-y)sinx+2y-3=0 B.(y-1)sinx+2y-3=0 C.(y+1)sinx+2y+1=0 D.-(y+1)sinx+2y+1=0 6、已知函数的图像如图所示,则 。 w.w.w.k.s.5.u.c.o.m 【0】 7、若函数在上至少出现个最大值,则的最小值 为_________________ (结果用表示)【】 8、函数 (>0,||< ,∈R)的部分图象如图所示,则函数表达式为 ( )【B】 A. B. C. D. Ø Ø 9、求函数的单调增区间【】 10、(2011年高考江苏卷)函数是常数, 的部分图象如图所示,则【】 11、在函数的一个周期内,当时有最大值,当时有最小值,若,则函数解析式=_______【】 12、(2010广东理)已知函数在时取得最大值4. (1) 求的最小正周期;【】 (2) 求的解析式;【】 (3) 若,求.【】 13、设,,其中为非零实常数. (1)若,,求;【】 (2)若,试讨论函数的奇偶性,并证明你的结论; 【当时, 是奇函数;当时,既不是奇函数,又不是偶函数】 (3)已知:对于任意,,恒有,当且仅当时,等号成立.若,求证:函数在上是递增函数. 【】查看更多