- 2021-05-13 发布 |
- 37.5 KB |
- 5页


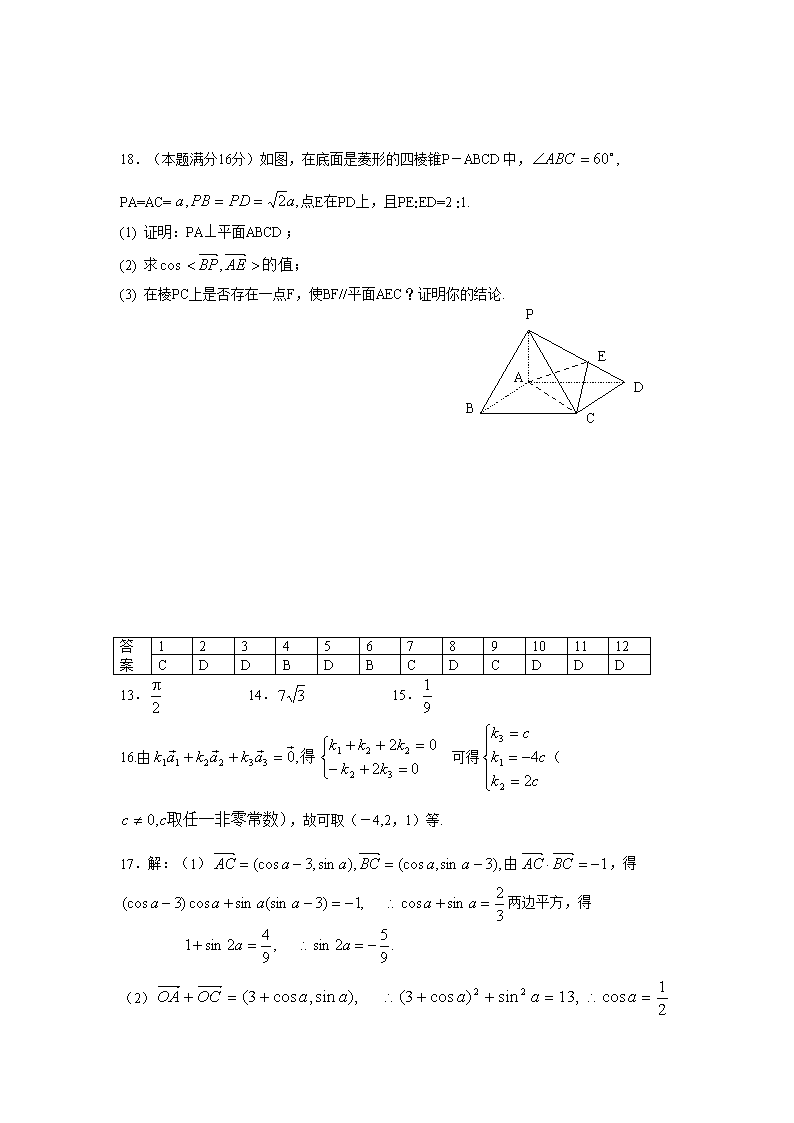
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
平面向量及空间向量高考数学专题训练
平面向量及空间向量高考数学专题训练(四) 一、选择题(本大题共 12 小题,每小题分 6,共 72 分) 1.设 1(a cos,), (b sin )3, ,且∥, 则锐角为( ) A. 6 B. 4 C. 3 D. 12 5 2.已知点 )0,2(A 、 )0,3(B ,动点 2),( xPBPAyxP 满足 ,则点 P 的轨迹是( ) A.圆 B. 椭圆 C. 双曲线 D. 抛物线 3.已知向量 值是相互垂直,则与且 kbabakba 2),2,0,1(),0,1,1( ( ) A. 1 B. 5 1 C. 5 3 D. 5 7 4.已知 ba , 是非零向量且满足 的夹角是与则 babababa ,)2(,)2( ( ) A. 6 B. 3 C. 3 2 D. 6 5 5.将函数 y=sinx 的图像上各点按向量 a ( 2,3 )平移,再将所得图像上各点的横坐标 变为原来的 2 倍,则所得图像的解析式可以写成( ) A.y=sin(2x+ 3 )+2 B.y=sin(2x- 3 )-2 C.y=( 32 1 x )-2 D.y=sin( 32 1 x )+2 6.若 A,B 两点的坐标是 A(3 cos ,3 sin ,1),B(2 ,cos 2 ,sin 1),| AB |的取值范围是 ( ) A. [0,5] B. [1,5] C. (1,5) D. [1,25] 7.从点 A(2,-1,7)沿向量 )12,9,8( a 方向取线段长|AB|=34,则点 B 的坐标为( ) A.(-9,-7,7) B.(-9,-7,7) 或(9,7,-7) C.(18,17,-17) D.(18,17,-17)或(-18,-17,17) 8.平面直角坐标系中,O 为坐标原点, 已知两点 A(3, 1), B(-1, 3),若点 C 满足 OC = OBOA , 其中α、β∈R 且α+β=1, 则点 C 的轨迹方程为 ( ) A. 01123 yx B. 5)2()1( 22 yx C. 02 yx D. 052 yx 9.已知空间四边形 ABCD 的每条边和对角线的长都等于 m,点 E,F 分别是 BC,AD 的 中点,则 AFAE 的值为 ( ) A. B. 2 1 C. 4 1 D. 4 3 10 . O 为 空 间 中 一 定 点 , 动 点 P 在 A,B,C 三 点 确 定 的 平 面 内 且 满 足 )()( ACABOAOP =0,则点 P 的轨迹一定过△ABC 的 ( ) A.外心 B.内心 C.重心 D. 垂心 11.在棱长为 1 的正方体 ABCD-A1B1C1D1 中,M、N 分别为 A1B1 与 BB1 的中点,那么直 线 AM 与 CN 所成的角为( ) A. 2 3arccos B. 10 10arccos C. arccos 5 3 D. arccos 5 2 12. 三 棱 锥 O-ABC 中 , 设 的中点,分别为 BCOA,,,, NMcOCbOBaOA , 点 G∈MN,MG:GN=2,则 分别等于则 zyxOCzOByOAxOG ,,, ( ) A. 3 1 , 3 1 , 3 1 B. 3 1 , 3 1 , 6 1 C. 3 1 , 6 1 , 3 1 D. 6 1 , 3 1 , 3 1 二、填空题(本大题共 4 小题,每小题 5 分,共 20 分) 13.已知 ),cos,1,(sin),sin,1,(cos ba 则向量 baba 与 的夹角为______ 14.已知空间三点 A(0,2,3), B(-2,1,6), C(1,-1,5),以 ACAB、 为边的平行四边形的面积为 15.已知向量 BABABAm tantan22 3)2sin5,2cos2( ,则的模为 的值为___ 16 . 若 对 n 个 向 量 naaa ,,, 21 存 在 n 个 不 全 为 零 的 实 数 ,,,, 21 nkkk 使 得 02211 nn akakak 成立,则称向量 naaa ,,, 21 为“线性相关”.依此规定,能说 明 )2,2(),1,1(),0,1( 321 aaa “ 线 性 相 关 ” 的 实 数 321 ,, kkk 依 次 可 以 取 _____________________(写出一组数值即可,不必考虑所有情况). 三、解答题(本大题共 4 小题,共 58 分) 17.(本题满分 13)已知 A(3,0),B(0,3),C(cos ).sin, (1)若 2sin,1 求 BCAC 的值; (2)若 . OC),,0(,13|| 的夹角与求且 OBOCOA A P C E 18.(本题满分 16 分)如图,在底面是菱形的四棱锥 P-ABCD 中, ,60ABC PA=AC= ,2, aPDPBa 点 E 在 PD 上,且 PE:ED=2 :1. (1) 证明:PA⊥平面 ABCD; (2) 求 的值; AEBP,cos (3) 在棱 PC 上是否存在一点 F,使 BF//平面 AEC?证明你的结论. 答 案 1 2 3 4 5 6 7 8 9 10 11 12 C D D B D B C D C D D D 13. 2 14. 37 15. 9 1 16. 由 得,0332211 akakak 02 02 32 221 kk kkk 可 得 ck ck ck 2 4 2 1 3 ( 取任一非零常数)cc ,0 ,故可取(-4,2,1)等. 17.解:(1) ),3sin,(cos),sin,3(cos aaBCaaAC 由 1 BCAC ,得 3 2sincos,1)3(sinsincos)3(cos aaaaaa 两边平方,得 .9 52sin,9 42sin1 aa (2) 2 1cos,13sin)cos3(),sin,cos3( 22 aaaaaOCOA D P B A P C E P B ,2 3sin,3),,0( aaa .2 33OCOB 设OB 与OC 的夹角为, 则 ,6,2 3 |||| cos = OCOB OCOB .6 的夹角为与OCOB 20.解:(1)因为底面 ABCD 是菱形, 60ABC ,所以 AB=AD=AC= 在△PAB 中,由 PA2+AB2=22=PB2,知 PA⊥AB.同理,PA⊥AD,所以 PA⊥平面 ABCD. (2)以 A 为坐标原点,直线 AD,AP 分别为 y 轴,z 轴,过 A 点垂直平面 PAD 的直线为 x 轴,建立空间直角坐标系如图. 由题设条件,相关各点的坐标分别为 )3 1,3 2,0(),,0,0(),0,2 1,2 3(),0,0,0( aaEaPaaBA ∴ ),2 1,2 3(),3 1,3 2,0( aaaBPaaAE ∴ 5 10 29 5 3 1 3 1 |||| ,cos 22 22 aa aa AEBP AEBPAEBP (3)∵ ),0,0(),0,,0(),0,2 1,2 3( aPaDaaC ∴ ).,0,0(),,2 1,2 3(),0,2 1,2 3( aAPaaaPCaaAC 设点 F 是棱 PC 上的点, 则 其中 ,10),,2 1,2 3( aaaPCPF ),2 1,2 3(),2 1,2 3(BPBF = aaaaaaPF ))1(,)1(2 1,)1(2 3( aaa . 得令 AEACBF 21 D , 3 1)1( 3 2 2 1)1(2 1 2 3)1(2 3 2 21 1 aa aaa aa 解得 .2 3,2 1,2 1 21 即 .2 3 2 1 2 1 AEACBF 时, ∴F 是 PC 的中点时 AEACBF ,,, 共面. 又∵ ,平面AECBF ∴当 F 是棱 PC 的中点时,BF .AEC// 平面查看更多