数学版年高考年模拟函数与基本初等函数函数的概念与性质
第二章 函数与基本初等函数I
第一节 函数的概念与性质
第一部分 六年高考荟萃
2010年高考题
一、 选择题
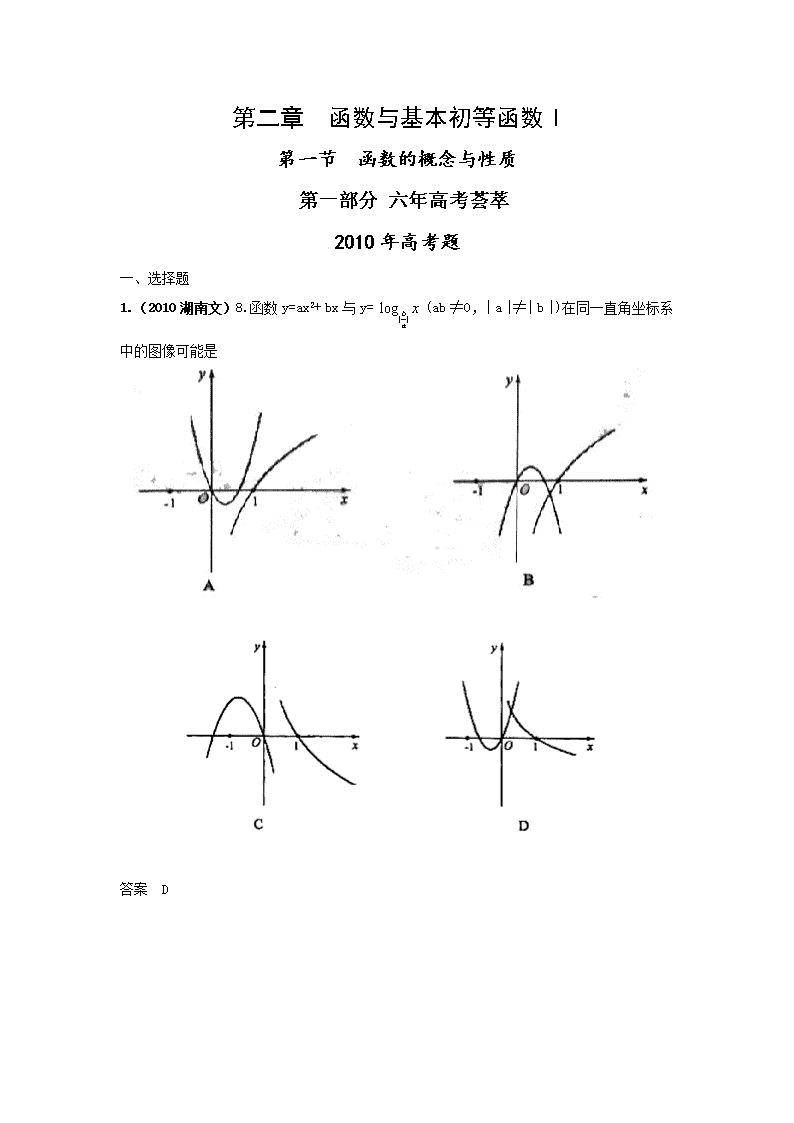
1.(2010湖南文)8.函数y=ax2+ bx与y= (ab ≠0,| a |≠| b |)在同一直角坐标系中的图像可能是
答案 D
2.(2010浙江理)(10)设函数的集合
,
平面上点的集合
,
则在同一直角坐标系中,中函数的图象恰好经过中两个点的函数的个数是
(A)4 (B)6 (C)8 (D)10
答案 B
解析:当a=0,b=0;a=0,b=1;a=,b=0; a=,b=1;a=1,b=-1;a=1,b=1时满足题意,故答案选B,本题主要考察了函数的概念、定义域、值域、图像和对数函数的相关知识点,对数学素养有较高要求,体现了对能力的考察,属中档题
3.(2010辽宁文)(4)已知,函数,若满足关于的方程,则下列选项的命题中为假命题的是
(A) (B)
(C) (D)
答案 C
解析:选C.函数的最小值是
等价于,所以命题错误.
4.(2010江西理)9.给出下列三个命题:
①函数与是同一函数;高☆考♂资♀源*网
②若函数与的图像关于直线对称,则函数与的图像也关于直线对称;
③若奇函数对定义域内任意x都有,则为周期函数。
其中真命题是
A. ①② B. ①③ C.②③ D. ②
答案 C
【解析】考查相同函数、函数对称性的判断、周期性知识。考虑定义域不同,①错误;排除A、B,验证③, ,又通过奇函数得,所以f(x)是周期为2的周期函数,选择C。
5.(2010重庆理)(5) 函数的图象
A. 关于原点对称 B. 关于直线y=x对称 C. 关于x轴对称 D. 关于y轴对称
答案 D
解析: 是偶函数,图像关于y轴对称
6.(2010天津文)(5)下列命题中,真命题是
(A)
(B)
(C)
(D)
答案A
【解析】本题主要考查奇偶数的基本概念,与存在量词、全称量词的含义,属于容易题。当m=0时,函数f(x)=x2是偶函数,所以选A.
【温馨提示】本题也可以利用奇偶函数的定义求解。
7.(2010天津理)(3)命题“若f(x)是奇函数,则f(-x)是奇函数”的否命题是
(A)若f(x) 是偶函数,则f(-x)是偶函数
(B)若f(x)不是奇函数,则f(-x)不是奇函数
(C)若f(-x)是奇函数,则f(x)是奇函数
(D)若f(-x)不是奇函数,则f(x)不是奇函数
答案 B
【解析】本题主要考查否命题的概念 ,属于容易题。
否命题是同时否定命题的条件结论,故否命题的定义可知B项是正确的。
【温馨提示】解题时要注意否命题与命题否定的区别。
8.(2010广东理)3.若函数f(x)=3x+3-x与g(x)=3x-3-x的定义域均为R,则
A.f(x)与g(x)均为偶函数 B. f(x)为偶函数,g(x)为奇函数
C.f(x)与g(x)均为奇函数 D. f(x)为奇函数,g(x)为偶函数
答案 D
【解析】.
9.(2010广东文)3.若函数与的定义域均为R,则
A. 与与均为偶函数 B.为奇函数,为偶函数
C. 与与均为奇函数 D.为偶函数,为奇函数
答案 D
解:由于,故是偶函数,排除B、C
由题意知,圆心在y轴左侧,排除A、C
在,,故,选D
10.(2010广东文)2.函数的定义域是
A. B. C. D.
答案 B
解:,得,选B.
11.(2010全国卷1理)(10)已知函数f(x)=|lgx|.若0
lge>0,知a>b,又c=lge, 作商比较知c>b,选B。
12.(2009广东卷理)若函数是函数的反函数,其图像经过点,则 ( )
A. B. C. D.
答案 B
解析 ,代入,解得,所以,选B.
13.(2009广东卷理)已知甲、乙两车由同一起点同时出发,并沿同一路线(假定为直线)行驶.甲车、乙车的速度曲线分别为(如图2所示).那么对于图中给定的,下列判断中一定正确的是 ( )
A. 在时刻,甲车在乙车前面
B. 时刻后,甲车在乙车后面
C. 在时刻,两车的位置相同
D. 时刻后,乙车在甲车前面
答案 A
解析 由图像可知,曲线比在0~、0~与轴所围成图形面积大,则在、时刻,甲车均在乙车前面,选A.
14.(2009安徽卷理)设<b,函数的图像可能是 ( )
答案 C
解析 ,由得,∴当时,取极大值0,当时取极小值且极小值为负。故选C。
或当时,当时,选C
15.(2009安徽卷文)设,函数的图像可能是 ( )
答案 C
解析 可得的两个零解.
当时,则
当时,则当时,则选C。
16.(2009江西卷文)函数的定义域为 ( )
A. B. C. D.
答案 D
解析 由得或,故选D.
17.(2009江西卷文)已知函数是上的偶函数,若对于,都有,且当时,,则的值为 ( )
A. B. C. D.
答案 C
解析 ,故选C.
18.(2009江西卷文)如图所示,一质点在平面上沿曲线运动,
速度大小不 变,其在轴上的投影点的运动速度的图象
大致为 ( )
A B C D
答案 B
解析 由图可知,当质点在两个封闭曲线上运动时,投影点的速度先由正到0、到负数,再到0,到正,故错误;质点在终点的速度是由大到小接近0,故错误;质点在开始时沿直线运动,故投影点的速度为常数,因此是错误的,故选.
19.(2009江西卷理)函数的定义域为 ( )
A. B. C. D.
答案 C
解析 由.故选C
20.(2009江西卷理)设函数的定义域为,若所有点构成一个正方形区域,则的值为 ( )
A. B. C. D.不能确定
答案 B
解析 ,,,,选B
21.(2009天津卷文)设函数则不等式的解集是( )
A. B.
C. D.
答案 A
解析 由已知,函数先增后减再增
当,令
解得。
当,
故 ,解得
【考点定位】本试题考查分段函数的单调性问题的运用。以及一元二次不等式的求解。
22.(2009天津卷文)设函数f(x)在R上的导函数为f’(x),且2f(x)+xf’(x)>x,x下面的不等式在R内恒成立的是 ( )
A. B. C. D.
答案 A
解析 由已知,首先令 ,排除B,D。然后结合已知条件排除C,得到A
【考点定位】本试题考察了导数来解决函数单调性的运用。通过分析解析式的特点,考查了分析问题和解决问题的能力。
23.(2009湖北卷理)设a为非零实数,函数( )
A、 B、
C、 D、
答案 D
解析 由原函数是,从中解得
即原函数的反函数是,故选择D
24..(2009湖北卷理)设球的半径为时间t的函数。若球的体积以均匀速度c增长,则球的表面积的增长速度与球半径 ( )
A.成正比,比例系数为C B. 成正比,比例系数为2C
C.成反比,比例系数为C D. 成反比,比例系数为2C
答案 D
解析 由题意可知球的体积为,则,由此可
,而球的表面积为,
所以,
即,故选
25.(2009四川卷文)已知函数是定义在实数集R上的不恒为零的偶函数,且对任意实数都有
,则的值是 ( )
A. 0 B. C. 1 D.
答案 A
解析 若≠0,则有,取,则有:
(∵是偶函数,则
)由此得于是
26.(2009福建卷理)函数的图象关于直线对称。据此可推测,对任意的非零实数a,b,c,m,n,p,关于x的方程的解集都不可能是 ( )
A. B C D
答案 D
解析 本题用特例法解决简洁快速,对方程中分别赋值求出代入求出检验即得.
27.(2009辽宁卷文)已知偶函数在区间单调增加,则满足<的x 取值范围是 ( )
(A)(,) B.[,) C.(,) D.[,)
答案 A
解析 由于f(x)是偶函数,故f(x)=f(|x|)
∴得f(|2x-1|)<f(),再根据f(x)的单调性
得|2x-1|< 解得<x<
28.(2009宁夏海南卷理)用min{a,b,c}表示a,b,c三个数中的最小值 ( )
设f(x)=min{, x+2,10-x} (x 0),则f(x)的最大值为
(A)4 (B)5 (C)6 (D)7
答案 C
29.(2009陕西卷文)函数的反函数为 ( )
(A) B.
(C) (D)学科
答案 D
解析 令原式 则
故 故选D.
30.(2009陕西卷文)定义在R上的偶函数满足:对任意的,有.则 ( )
(A) B.
C. D.
答案 A
解析 由等价,于则在
上单调递增, 又是偶函数,故在
单调递减.且满足时, , ,得
,故选A.
31.(2009陕西卷理)定义在R上的偶函数满足:对任意
的,有.
则当时,有 ( )
(A) B.
C. C. D.
答案 C
32.(2009四川卷文)已知函数是定义在实数集R上的不恒为零的偶函数,且对任意实数都有,则的值是 ( )
A. 0 B. C. 1 D.
答案 A
解析 若≠0,则有,取,则有:
(∵是偶函数,则 )
由此得于是,
33.(2009湖北卷文)函数的反函数是 ( )
A. B.
C. D.
答案 D
解析 可反解得且可得原函数中y∈R、y≠-1所以且x∈R、x≠-1选D
34.(2009湖南卷理)如图1,当参数时,连续函数
的图像分别对应曲线和 , 则 ( )
A B
C D
答案 B
解析 解析由条件中的函数是分式无理型函数,先由函
数在是连续的,可知参数,即排除C,D项,又取,知对应函数值,由图可知所以,即选B项。
35.(2009湖南卷理)设函数在(,+)内有定义。对于给定的正数K,定义函数 ( )
取函数=。若对任意的,恒有=,则 ( )
A.K的最大值为2 B. K的最小值为2
C.K的最大值为1 D. K的最小值为1
答案 D
解析 由知,所以时,,当时,,所以即的值域是,而要使在上恒成立,结合条件分别取不同的值,可得D符合,此时。故选D项。
36.(2009天津卷理)已知函数若则实数
的取值范围是 ( )
A B C D
【考点定位】本小题考查分段函数的单调性问题的运用。以及一元二次不等式的求解。
解析:由题知在上是增函数,由题得,解得,故选择
C。
37.(2009四川卷理)已知函数是定义在实数集上的不恒为零的偶函数,且对任意实数都有,则的值是 ( )
A.0 B. C.1 D.
【考点定位】本小题考查求抽象函数的函数值之赋值法,综合题。(同文12)
答案 A
解析 令,则;令,则
由得,所以
,故选择A。
38.(2009福建卷文)下列函数中,与函数 有相同定义域的是 ( )
A . B. C. D.
答案 A
解析 解析 由可得定义域是的定义域;的定义域是≠0;的定义域是定义域是。故选A.
39.(2009福建卷文)定义在R上的偶函数的部分图像如右图所示,则在上,下列函数中与的单调性不同的是 ( )
A.
B.
C.
D.
答案 C
解析 解析 根据偶函数在关于原点对称的区间上单调性相反,故可知求在上单调递减,注意到要与的单调性不同,故所求的函数在上应单调递增。而函数在上递减;函数在时单调递减;函数在(上单调递减,理由如下y’=3x2>0(x<0),故函数单调递增, 显然符合题意;而函数,有y’=-<0(x<0),故其在(上单调递减, 不符合题意,综上选C。
40.(2009重庆卷文)把函数的图像向右平移个单位长度,再向下平移个单位长度后得到图像.若对任意的,曲线与至多只有一个交点,则 的最小值为 ( )
A. B. C. D.
答案 B
解析 根据题意曲线C的解析式为则方程
,即,即对任意
· 恒成立,于是的最大值,令则
· 由此知函数在(0,2)上为增函数,在上为减函数,所以当时,函数取最大值,即为4,于是。
41.(2009重庆卷理)若是奇函数,则 .
答案
解析 解法1
42(2009上海卷文) 函数f(x)=x3+1的反函数f-1(x)=_____________.
答案
解析 由y=x3+1,得x=,将y改成x,x改成y可得答案。
44(2009北京文)已知函数若,则 .
.w.w.k.s.5 答案
.w 解析 5.u.c本题主要考查分段函数和简单的已知函数值求的值. 属于基础知识、基本运算的考查.
由,无解,故应填.
45.(2009北京理)若函数 则不等式的解集为____________.
答案
解析 本题主要考查分段函数和简单绝对值不等式的解法. 属于基础知识、基本运算
的考查.
(1)由.
(2)由.
∴不等式的解集为,∴应填.
46.(2009江苏卷)已知,函数,若实数、满足,则、的大小关系为 .
解析 考查指数函数的单调性。
,函数在R上递减。由得:m0)在区间上有四个不同的根,则
答案 -8
解析 因为定义在R上的奇函数,满足,所以,所以, 由为奇函数,所以函数图象关于直线对称且,由知,所以函数是以8为周期的周期函数,又因为在区间[0,2]上是增函数,所以在区间[-2,0]上也是增函数.如图所示,那么方程f(x)=m(m>0)在区间上有四个不同的根,不妨设由对称性知所以
-8 -6 -4 -2 0 2 4 6 8
y
x
f(x)=m (m>0)
【命题立意】:本题综合考查了函数的奇偶性,单调性,
对称性,周期性,以及由函数图象解答方程问题,
运用数形结合的思想和函数与方程的思想解答问题.
14.(2009四川卷文)设是已知平面上所有向量的集合,对于映射,记的象为。若映射满足:对所有及任意实数都有,则称为平面上的线性变换。现有下列命题:
①设是平面上的线性变换,,则
②若是平面上的单位向量,对,则是平面上的线性变换;
③对,则是平面上的线性变换;
④设是平面上的线性变换,,则对任意实数均有。
其中的真命题是 (写出所有真命题的编号)
答案 ①③④
解析 ①:令,则故①是真命题
同理,④:令,则故④是真命题
③:∵,则有
是线性变换,故③是真命题
②:由,则有
∵是单位向量,≠0,故②是假命题
【备考提示】本小题主要考查函数,对应及高等数学线性变换的相关知识,试题立意新
颖,突出创新能力和数学阅读能力,具有选拔性质。
48.(2009年广东卷文)(本小题满分14分)
已知二次函数的导函数的图像与直线平行,且在=-1处取得最小值m-1(m).设函数
(1)若曲线上的点P到点Q(0,2)的距离的最小值为,求m的值
(2) 如何取值时,函数存在零点,并求出零点.
解 (1)设,则;
又的图像与直线平行
又在取极小值, ,
, ;
, 设
则
;
(2)由,
得
当时,方程有一解,函数有一零点;
当时,方程有二解,若,,
函数有两个零点;若,
,函数有两个零点;
当时,方程有一解, , 函数有一零点
49.(2009浙江理)(本题满分14分)已知函数,,
其中.
(I)设函数.若在区间上不单调,求的取值范围;
(II)设函数 是否存在,对任意给定的非零实数,存在惟一
的非零实数(),使得成立?若存在,求的值;若不存
在,请说明理由.
解 (I)因,,因在区间上不单调,所以在上有实数解,且无重根,由得
,令有,记则在上单调递减,在上单调递增,所以有, 于是,得,而当时有在 上有两个相等的实根,故舍去,所以;
(II)当时有;
当时有,因为当时不合题意,因此,
下面讨论的情形,记A,B=(ⅰ)当时,在上单调递增,所以要使成立,只能且,因此有,(ⅱ)当时,在上单调递减,所以要使成立,只能且,因此,综合(ⅰ)(ⅱ);
当时A=B,则,即使得成立,因为在上单调递增,所以的值是唯一的;
同理,,即存在唯一的非零实数,要使成立,所以满足题意.
7.(2009江苏卷)(本小题满分16分)
设为实数,函数.
(1)若,求的取值范围;
(2)求的最小值;
(3)设函数,直接写出(不需给出演算步骤)不等式的解集.
解 本小题主要考查函数的概念、性质、图象及解一元二次不等式等基础知识,考查灵活运用数形结合、分类讨论的思想方法进行探索、分析与解决问题的综合能力。满分16分
(1)若,则
(2)当时,
当时,
综上
(3)时,得,
当时,;
当时,△>0,得:
讨论得:当时,解集为;
当时,解集为;
当时,解集为.
50.(2009年上海卷理)已知函数的反函数。定义:若对给定的实数,函数与互为反函数,则称满足“和性质”;若函数与互为反函数,则称满足“积性质”。
(1) 判断函数是否满足“1和性质”,并说明理由;
(2) 求所有满足“2和性质”的一次函数;
(3) 设函数对任何,满足“积性质”。求的表达式。
解 (1)函数的反函数是
而其反函数为
故函数不满足“1和性质”
(2)设函数满足“2和性质”,
…….6分
而得反函数………….8分
由“2和性质”定义可知=对恒成立
即所求一次函数为………..10分
(3)设,,且点在图像上,则在函数图象上,
故,可得, ......12分
令,则。,即。 ......14分
综上所述,,此时,其反函数就是,
而,故与互为反函数 。
2005—2008年高考题
一、选择题
1.(2008年山东文科卷)设函数则的值为( )
A. B. C. D.
答案 A
2.(07天津)在上定义的函数是偶函数,且,若在区间 是减函数,则函数 ( )
A.在区间上是增函数,区间上是增函数
B.在区间上是增函数,区间上是减函数
C.在区间上是减函数,区间上是增函数
D.在区间上是减函数,区间上是减函数
答案 B
3. (07福建)已知函数为R上的减函数,则满足的实数的取值范围
是 ( )
A. B.
C. D.
答案 C
4.(07重庆)已知定义域为R的函数在区间上为减函数,且函数为偶函数,则 ( )
A. B.
C. D.
答案 D
5.(07安徽)图中的图象所表示的函数的解析式为 ( )
A. (0≤x≤2)
B. (0≤x≤2)
C. (0≤x≤2)
D. (0≤x≤2)
答案 B
6.(2005年上海13)若函数,则该函数在上是 ( )
A.单调递减;无最小值 B.单调递减;有最小值
C.单调递增;无最大值 D.单调递增;有最大值
答案 A
二、填空题
7.(2007上海春季5)设函数是奇函数. 若
则 .
答案
8.(2007年上海)函数的定义域是 .
答案
9.(2006年安徽卷)函数对于任意实数满足条件,若 则_______________。
答案 -
解析 。
10.(2006年上海春)已知函数是定义在上的偶函数. 当时,
,则当时, .
答案 -x-x4
三、解答题
11.(2007广东) 已知a是实数,函数,如果函数在区间
上有零点,求a的取值范围.
解析 若 , ,显然在上没有零点, 所以 .
令 , 解得
①当 时, 恰有一个零点在上;
②当,即时,在
上也恰有一个零点.
③当在上有两个零点时, 则
或
解得或
综上所求实数的取值范围是或.
第二部分 四年联考汇编
2010年联考题
题组二(5月份更新)
一、选择题
1.(安徽两地三校国庆联考)在上定义的函数是偶函数,且,若在区间 是减函数,则函数 ( )
A.在区间上是增函数,区间上是增函数
B.在区间上是增函数,区间上是减函数
C.在区间上是减函数,区间上是增函数
D.在区间上是减函数,区间上是减函数
答案 B
2.(昆明一中一次月考理)下列函数既是奇函数,又在区间上单调递减的是
A. B. C. D.
答案:C
3.(岳野两校联考)已知函数,若,则( )
A. B. C. D.
答案 C
4.(安徽两地三校国庆联考)(安徽两地三校国庆联考)函数的反函数为 ( )
(A) B.
(C) (D)
答案 D
5.(师大附中理)已知函数,如果存在实数使得对任意实数,都有,则的最小值是
A. B.4 C. D.
答案:B
6.(安徽六校联考)函数零点的个数是( )
A. B. C. D.
答案C
7.如果函数对任意的实数,存在常数M,使得不等式恒成立,那么就称函数为有界泛函,下面四个函数:
①; ②;③; ④.
其中属于有界泛函的是( ).
A. ①② B. ③④ C. ①③ D. ②④
答案 B
8.(师大附中理)中,如果边满足,则
A.一定是锐角 B.一定是钝角 C.一定是直角 D.以上情况都有可能
答案:A
9.(三明市三校联考)函数f(x) =的零点所在的大致区间是 ( )
A.(1, 2) B.(2,e) C.(e,3) D.(e,+∞)
答案B
10.(昆明一中一次月考理)二次方程有一个正根和一个负根的充分不必要条件是
A、 B、 C 、 D、
答案:C
11.(昆明一中一次月考理)已知是其定义域上的单调递增函数,它的反函数是,且的图象过两点,若,则x的取值范围是
A、 B、 C、 D、
答案:B
二、填空题
1. 对于任意,函数的值恒大于零,那么的取值范围是 .
答案
2.(安徽两地三校国庆联考)若函数f (x) = 4x3-ax+3的单调递减区间是,则实数a的值为
答案 3
三、解答题
1.(池州市七校元旦调研)设函数有两个极值点,且,
求的取值范围,并讨论的单调性;
解: (I)
令,其对称轴为。由题意知是方程的两个均大于的不相等的实根,其充要条件为,得
⑴当时,在内为增函数;
⑵当时,在内为减函数;
⑶当时,在内为增函数;
2.(本小题满分13分)已知函数.
(I)求的单调区间;
(II)若不等式恒成立,求实数的取值组成的集合.
解:(I)由已知得.因为,……………………2分
所以当.
故区间为的单调递减区间,
区间为的单调递增区间. ……………………5分
(II)(i)当时,.
令,则.……7分
由(1)知当时,有,所以,
即得在上为增函数,所以,
所以. ……………………10分
(ii)当时,.
由①可知,当时,为增函数,所以,
所以。
综合以上,得.故实数的取值组成的集合为. ……………………13分
3. (安庆市四校元旦联考)(满分16分)设函数,,当时,取得极值。
⑴求的值,并判断是函数的极大值还是极小值;
⑵当时,函数与的图象有两个公共点,求的取值范围。
解:(1)由题意
当时,取得极值, 所以
即
此时当时,,当时,,
是函数的最小值。
(2)设,则 ,
设,
,令解得或
列表如下:
__
0
+
函数在和上是增函数,在上是减函数。
当时,有极大值;当时,有极小值
函数与的图象有两个公共点,函数与的图象有两个公共点
或
4. (哈师大附中、东北师大附中、辽宁省实验中学)已知函数
(1)若函数在定义域内单调递增,求的取值范围;
(2)若且关于x的方程在上恰有两个不相等的实数根,求实数的取值范围;
(3)设各项为正的数列满足:求证:
解:(1)
依题意在时恒成立,即在恒成立.
则在恒成立,即
当时,取最小值
∴的取值范围是 ……
(2)
设则列表:
极大值
¯
极小值
∴极小值,极大值,又 ……
方程在[1,4]上恰有两个不相等的实数根.
则, 得 …………
(3)设,则
在为减函数,且故当时有.
假设则,故
从而
即,∴ …………
题组一(1月份更新)
一、选择题
1、(2009广东三校一模)2.函数在处取到极值,则的值为
答案 B
2、(2009昆明市期末)函数的最小值是 ( )
A. B. C.9 D.27
答案 B
3、(2009滨州一模)设函数,表示不超过的最大整数,则函数的值域为
A . B . C . D .
答案 B
4、(2009昆明一中第三次模拟)设,则在下列区间中,使函数有零点的区间是( )
A. B C. D.
答案 D
5、(2009东莞一模)下列四个函数中,在(0,1)上为增函数的是
A. B C. D.
答案 A
6、(2009牟定一中期中)将函数的图象按向量平移后得到函数的图象,则 ( )
A. B. C. D.
答案 A
7、(2009聊城一模)若a>2,则函数在区间(0,2)上恰好有 ( )
A.0个零点 B.1个零点 C.2个零点 D.3个零点
答案 B
8、(2009茂名一模)已知函数是定义域为的偶函数,且,若在上是减函数,那么在上是 ( )
A. 增函数 B. 减函数 C. 先增后减的函数 D. 先减后增的函数
答案 A
9、(2009玉溪一中期中)函数的图像过点,则函数的图像过( )
(A) (B) (C) (D)
答案 C
二、填空题
1、(2009滨州一模)给出下列四个结论:
①命题“的否定是“”;
②“若则”的逆命题为真;
③函数(x)有3个零点;
④对于任意实数x,有
且x>0时,则x<0时
其中正确结论的序号是 .(填上所有正确结论的序号)
答案 ①④
2、(2009宣威六中第一次月考)已知函数, .
答案 -2
3、(2009泰安一模)已知函数y=f(x)是R上的偶函数,对于x∈R都
有f(x+60=f(x)+f(3)成立,当,且时,都有给出下列命题:
①f(3)=0;
②直线x=一6是函数y=f(x)的图象的一条对称轴;
③函数y=f(x)在[一9,一6]上为增函数;
④函数y=f(x)在[一9,9]上有四个零点.
其中所有正确命题的序号为______________(把所有正确命题的序号都填上)
答案 ①②④
4、(2009上海闸北区)函数的定义域为___________.
答案
5、(2009重点九校联考)函数的定义域为 .
答案
三、解答题
1、(2009上海八校联考)对定义在上,并且同时满足以下两个条件的函数称为函数。
① 对任意的,总有;
② 当时,总有成立。
已知函数与是定义在上的函数。
(1)试问函数是否为函数?并说明理由;
(2)若函数是函数,求实数组成的集合;
解:(1)当时,总有,满足①,
当时,
,满足②
(2)为增函数,
由 ,得,
即
因为
所以 与不同时等于1
;
当时,;
综合上述:
2、(2009滨州一模)设函数
(I)若直线l与函数的图象都相切,且与函数的图象相切于点
(1,0),求实数p的值;
(II)若在其定义域内为单调函数,求实数p的取值范围;
解:(Ⅰ)方法一:∵,
∴.
设直线,
并设l与g(x)=x2相切于点M()
∵ ∴2
∴
代入直线l方程解得p=1或p=3.
方法二:
将直线方程l代入 得
∴
解得p=1或p=3 .
(Ⅱ)∵,
①要使为单调增函数,须在恒成立,
即在恒成立,即在恒成立,
又,所以当时,在为单调增函数; ②要使为单调减函数,须在恒成立,
即在恒成立,即在恒成立,
又,所以当时,在为单调减函数.
综上,若在为单调函数,则的取值范围为或.
3、(2009上海十校联考)已知函数,有反函数,且函数的最大值为,求实数的值.
解:因为函数有反函数,所以在定义域内是一一对应的
函数的对称轴为,所以或
若,在区间上函数是单调递增的,所以,解得,符合
若,在区间上函数是单调递减的,所以
,解得,与矛盾,舍去
综上所述,满足题意的实数的值为
4、(2009江门一模)已知函数,是常数,.
⑴若是曲线的一条切线,求的值;
⑵,试证明,使.
⑴-------1分,解得,或-------2分
当时,,,所以不成立-------3分
当时,由,即,得-----5分
⑵作函数-------6分
,函数在上的图象是一条连续不断的曲线------7分,------8分
①若,,,使,即-------10分www.ks5u.com
②若,,,
,当时有最小值,且当时-------11分,
所以存在(或)从而,使,即-------12分
5、(2009南华一中12月月考)设函数在及时取得极值.
(Ⅰ)求a、b的值;
(Ⅱ)若对于任意的,都有成立,求c的取值范围.
解:(Ⅰ),
因为函数在及取得极值,则有,.
即解得,.………………………6分
(Ⅱ)由(Ⅰ)可知,,
. ………………………7分
当时,;
当时,;
当时,. ………………………8分
所以,当时,取得极大值,又,.
则当时,的最大值为. ………………………10分
因为对于任意的,有恒成立,
所以 ,
解得 或,
因此的取值范围为.………………………12分
2009年联考题
一、选择题
1. (北京市东城区2009年3月高中示范校高三质量检测文理)函数的定义域是,若对于任意的正数,函数都是其定义域上的增函数,则函数的图象可能是 ( )
答案 A
2.(2009龙岩一中)函数的定义域是 ( )
A. B. C. D.
答案 B
3.(2009湘潭市一中12月考)已知定义在R上的函数满足,且
,, ( )
A. B. C. D.
答案 A
4.(2009广东三校一模)定义在上的函数是奇函数又是以为周期的周期函数,则
等于 ( )
A.-1 B.0 C.1 D.4
答案 B
5.(安徽省合肥市2009届高三上学期第一次教学质量检测)函数在上单调,则的取值范围是 ( )
A. B.
C. D.
答案 A
6.(黄山市2009届高中毕业班第一次质量检测)对于函数定义域中任意
有如下结论:①;
②; ③;
④。上述结论中正确结论的序号是 ( )
A.② B.②③ C.②③④ D.①②③④
答案 B
7.(福州市普通高中2009年高中毕业班质量检查)已知函数
两函数的图像的交点个数
为 ( )
A.1 B.2 C.3 D.4
答案 B
8.(福州市普通高中2009年高中毕业班质量检查)已知
,则不等式
的解集是 ( )
A.(—2,0) B.
C. D.
答案 C
9.(江门市2009年高考模拟考试)设函数的定义域为,的定义域为,则 ( )
A. B. C. D.
答案 C
10.(2009年深圳市高三年级第一次调研考试数学(文科))设,又记
则 ( )
A. B. C. D.
答案 D
11.(银川一中2009届高三年级第一次模拟考试)设函数是奇函数,并且在R上为增函
数,若0≤≤时,f(msin)+f(1—m)>0恒成立,则实数m的取值范围是( )
A.(0,1)B.(-∞,0)C. D.(-∞,1)
答案 D
二、填空题
12.(2009年龙岩市普通高中毕业班单科质量检查)已知函数为上的奇函数,
当时,.若,则实数 .
答案
13.(银川一中2009届高三年级第一次模拟考试)给出定义:若(其中为整数),则叫做离实数最近的整数,记作,即. 在此基础上给出下列关于函数的四个命题:
①函数的定义域是R,值域是[0,];
②函数的图像关于直线对称;
③函数是周期函数,最小正周期是1;
④ 函数在上是增函数;
则其中真命题是__ .
答案 ①②③
14.(安徽省示范高中皖北协作区2009年高三联考)已知函数,则不
等式的解集为
答案
15.(北京市石景山区2009年4月高三一模理)函数,则,若,则实数的取值范围是
答案
16. (北京市西城区2009年4月高三一模抽样测试文)设a为常数,.
若函数为偶函数,则=__________;=_______.
答案 2,8
17.(2009丹阳高级中学一模)若函数在上是增函数,则的取
值范围是____________。
答案
三、解答题
18.(银川一中2009届高三年级第一次模拟考试)设函数。
(1)画出函数y=f(x)的图像;
(2)若不等式,(a¹0,a、bÎR)恒成立,求实数x的范围。
1
1
2
x
y
解:(1)
(2)由|a+b|+|a-b|≥|a|f(x)
得
又因为
则有2≥f(x)
解不等式 2≥|x-1|+|x-2|
得
2007—2008年联考题
一、选择题
1.(陕西长安二中2008届高三第一学期第二次月考)定义在R上的偶函数满足
,且在[-1,0]上单调递增,设, ,,
则大小关系是 ( )
A. B. C. D.
答案 D
2.(陕西长安二中2008届高三第一学期第二次月考)函数是 ( )A.奇函数 B.偶函数
C.既是奇函数又是偶函数 D.非奇非偶函数
答案 D
3.(陕西长安二中2008届高三第一学期第二次月考)设f(x)是定义在R上的函数,且在
(-∞,+∞)上是增函数,又F(x)=f(x)-f(-x),那么F(x)一定是 ( )
A.奇函数,且在(-∞,+∞)上是增函数 B.奇函数,且在(-∞,+∞)上是减函数
C.偶函数,且在(-∞,+∞)上是增函数 D.偶函数,且在(-
∞,+∞)上是减函数
答案 A
4.(广东省2008届六校第二次联考)如图所示是某池塘中浮萍的面积
与时间(月)的关系: , 有以下叙述:
①这个指数函数的底数为2;
②第5个月时, 浮萍面积就会超过30;
③浮萍从4蔓延到12需要经过1.5个月;
④浮萍每月增加的面积都相等;
⑤若浮萍蔓延到2, 3, 6所经过的时间分别是,
则.其中正确的是 ( )
A.①② B.①②③④ C.②③④⑤ D. ①②⑤
答案 D
5.(2007届岳阳市一中高三数学能力题训练).映射f:A→B,如果满足集合B中的任意一
个元素在A中都有原象,则称为“满射”。已知集合A中有4个元素,集合B中有3个元素,那么从A到B的不同满射的个数为 ( )
A.24 B.6 C.36 D.72
答案 C
二、填空题
6.(2007届岳阳市一中高三数学能力题训练)若对于任意a[-1,1], 函数f(x) = x+ (a
-4)x + 4-2a的值恒大于零, 则x的取值范围是
答案 (
7.(2007年江苏省南京师范大学附属中学)已知函数,给出以下三个条件:
(1) 存在,使得;
(2) 成立;
(3) 在区间上是增函数.
若同时满足条件 和 (填入两个条件的编号),则
的一个可能的解析式为 .
答案 满足条件(1)(2)时,等;满足条件(1)(3)时,等;满足条件(2)(3)时,等.
三、解答题
8.(2007年安徽省六校)已知函数,在R上有定义,对任意的有 且
(1)求证:为奇函数
(2)若, 求的值
解(1)对,令x=u-v则有f(-x)=f(v-u)=f(v)g(u)-g(v)f(u)=f(u-v)=-[f(u)g(v)-
g(u)f(v)]=-f(x) ………………4分
(2)f(2)=f{1-(-1)}=f(1)g(-1)-g(1)f(-1)=f(1)g(-1)+g(1)f(1)=f(1){g(-1)+g(1)}
∵f(2)=f(1)≠0
∴g(-1)+g(1)=1 …………………8分