苏州市高考考前指导卷3第8稿

苏州市高考考前指导卷3第8稿

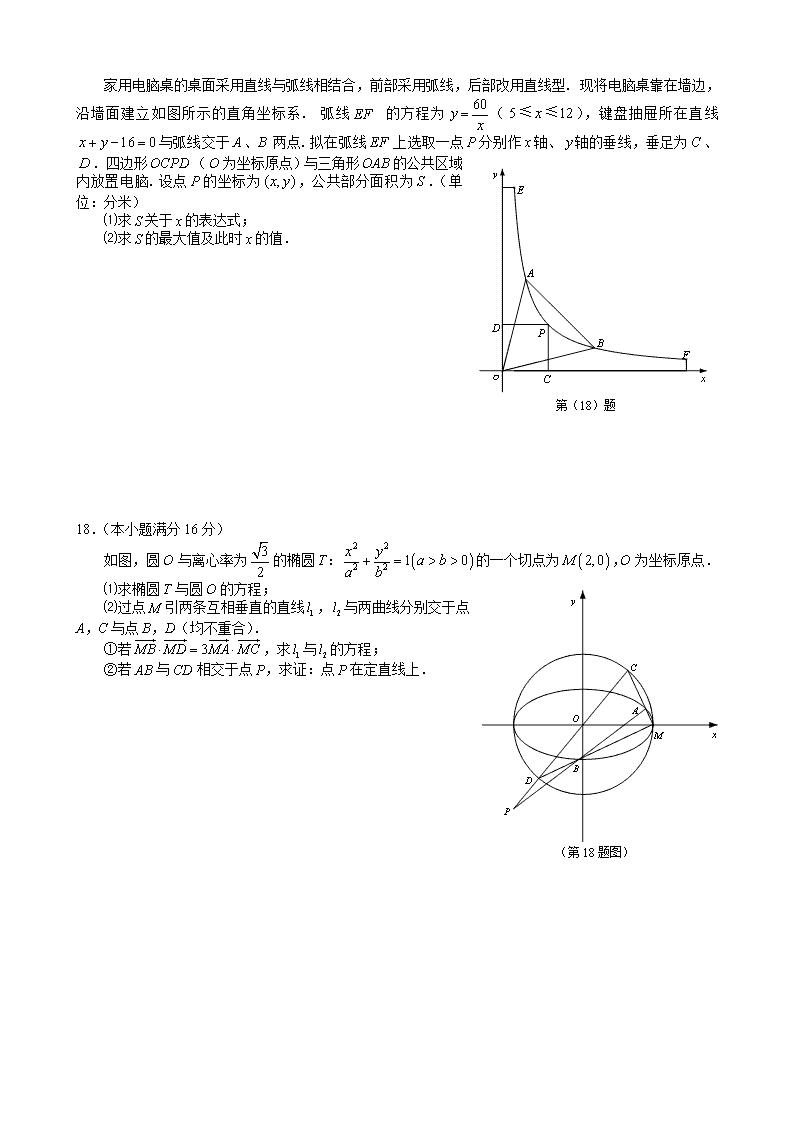
苏州市2015届高考考前指导卷 一、填空题：本大题共14小题，每小题5分，共计70分．不需要写出解答过程，请把答案直接填在答题卡相应位置上．‎ ‎1．满足的集合A的个数为 ▲ ．‎ ‎2．设复数（i为虚数单位，），若，则复数z的虚部为 ▲ ．‎ ‎3．在平面直角坐标系中，若双曲线的渐近线方程为，其一个焦点坐标为（5，0），则此双曲线的标准方程为 ▲ ． ‎ N S←40‎ 开始 k←1‎ k←k＋1‎ S≤0‎ Y 输出k 结束 S←S－2k ‎（第5题图）‎ ‎4．口袋内装有一些大小相同的红球、白球和黑球，从中摸出1个球，摸出红球的概率是0.42，摸出白球的概率是0.28，则摸出黑球的概率是 ▲ ．‎ ‎5．右图是一个算法流程图，则输出k的值是 ▲ ．‎ ‎6．已知函数f(x)＝ (ω＞0)的最大值与最小正周期相同，则函数 f(x)在[－1,1]上的单调增区间为 ▲ ．‎ ‎7．已知正三棱锥的底面边长为3，高为h,若正三棱锥的侧面积与体积的比为 ‎，则正三棱锥的高为 ▲ ．‎ ‎8．设等差数列的前和为，且是公差为的等差数列，则的 值组成的集合为 ▲ ． ‎ ‎9．直线与圆交于点,且为整数.则所有满足条件的正整数的和 为 ▲ ．‎ ‎10．已知函数f(x)＝mx3＋nx2的图象在点(－1, 2)处的切线恰好与直线3x＋y＝0平行，若f(x)在区间[t，t＋1]上单调递减，则实数t的取值范围是 ▲ ． ‎ ‎11‎（第12题图）‎ ．已知函数，若f(a) + f(a+1) > 2，则实数a的取值范围是 ▲ ． ‎ ‎12．如图，边长为2的正方形ABCD的内切圆与AB切于M，与BC切于N，P为圆周上任意一点，则的最大值为 ▲ ． ‎ ‎13．设均为正实数，且，则的最小值为 ▲ ． ‎ ‎14．已知函数，若恰有两组解，使得在定义域上的值域也为 ‎，则实数的取值范围为 ▲ ． ‎ 二、解答题：本大题共6小题，共计90分．请在答题卡指定区域内 作答，解答时应写出必要的文字说明、证明过程或演算步骤．‎ ‎15．（本小题满分14分）‎ 已知向量m＝(sin x，－1)，n＝(cos x, 3)．‎ ‎ （1）当m∥n时，求的值；‎ ‎ （2）已知在锐角△ABC中，角A，B，C的对边分别为a，b，c，c＝2asin(A＋B)，‎ 函数f(x)＝(m＋n)·m，求 的取值范围．‎ ‎（第16题图）‎ ‎16．（本小题满分14分）‎ 在四棱锥中，底面为梯形，,,,，平面平面，，分别是上的点，且．求证：‎ ‎（1） 平面；‎ ‎（2） 平面平面．‎ ‎ ‎ ‎17．（本小题满分14分）‎ 第（18）题 家用电脑桌的桌面采用直线与弧线相结合，‎ 前部采用弧线，后部改用直线型. 现将电脑桌靠在墙边，沿墙面建立如图所示的直角坐标系.弧线EF的方程为（），键盘抽屉所在直线与弧线交于A、B两点.拟在弧线EF上选取一点分别作轴、轴的垂线，垂足为、．四边形（为坐标原点）与三角形的公共区域内放置电脑.设点的坐标为，公共部分面积为．（单位：分米）‎ ‎⑴求关于的表达式；‎ ‎⑵求的最大值及此时的值．‎ ‎18．（本小题满分16分）‎ 如图，圆O与离心率为的椭圆T：的一个切点为，O为坐标原点．‎ ‎（第18题图）‎ ‎⑴求椭圆T与圆O的方程；‎ ‎⑵过点M引两条互相垂直的直线，与两曲线分别交于点A，C与点B，D（均不重合）．‎ ‎①若，求与的方程；‎ ‎②若AB与CD相交于点P，求证：点P在定直线上．‎ ‎19．（本小题满分16分）‎ 已知数列中，，，其前项和为满足（）．‎ ‎（1）试求数列的通项公式；‎ ‎（2）令，是数列的前项和．‎ ①若，不等式对一切的自然数都成立，求的最小值；‎ ②证明：对任意给定的，均存在，使得当时，恒成立．‎ ‎20．（本小题满分16分）‎ 已知函数，．‎ ‎（1）当a = b = 1时，求函数的单调区间；‎ ‎（2）当a = 1，b = - 1时，试比较与的大小；‎ ‎（3）若任意的a > 0，总存在正数x0，使得成立，求实数b的取值范围．‎ 苏州市2015届高考考前指导卷参考答案 一、填空题 ‎1．4 2．－1 3． 4．0.3 5．6 6． 7． ‎ ‎8． 9．8 10． 11． 12． 13． 14．‎ 二、解答题 ‎15．解　（1）由m∥n，可得3sin x＝－cos x，‎ ‎ 于是tan x＝－，∴＝＝＝－．‎ ‎ （2）在△ABC中A＋B＝π－C，于是 sin(A＋B)＝sin C，‎ ‎ 由正弦定理，得sin C＝2sin Asin C，‎ ‎ ∵sin C≠0，∴sin A＝．又△ABC为锐角三角形，‎ ‎ ∴A＝，于是 0），，‎ 令，得．‎ 令，得，∴的单调减区间为；‎ 令，得，∴的单调增区间为．‎ ‎（2）当a = 1，b = - 1时，．‎ 设，则≤0恒成立．‎ ‎∴在（0，+¥）上是减函数，又，则 当xÎ（0，1）时，>；‎ 当x = 1时，=；‎ 当xÎ（1，+¥）时，<．‎ ‎（3），即（x > 0）．‎ ‎① 若b≥0，取a = 1，考察函数．∵，‎ 令，得x = 4．‎ x ‎（0，4）‎ ‎4‎ ‎（4，+¥）‎ + ‎0‎ - ‎↗‎ 极大值 ‎↘‎ ‎∴．则< 0恒成立，即不存在正数x0，使．‎ ‎②若b < 0，（x > 0），也即（*）．‎ 先证，设，则．‎ 令，得．‎ x ‎（0，）‎ ‎（，+¥）‎ - ‎0‎ + ‎↘‎ 极小值 ‎↗‎ ‎∴．则> 0恒成立．‎ ‎∴．则．‎ 令，则．‎ 令，即 取，则当t > t0时，成立．‎ 即存在，使得．‎ 综上所述，实数b的取值范围为（-¥，0）．‎