- 2021-05-13 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
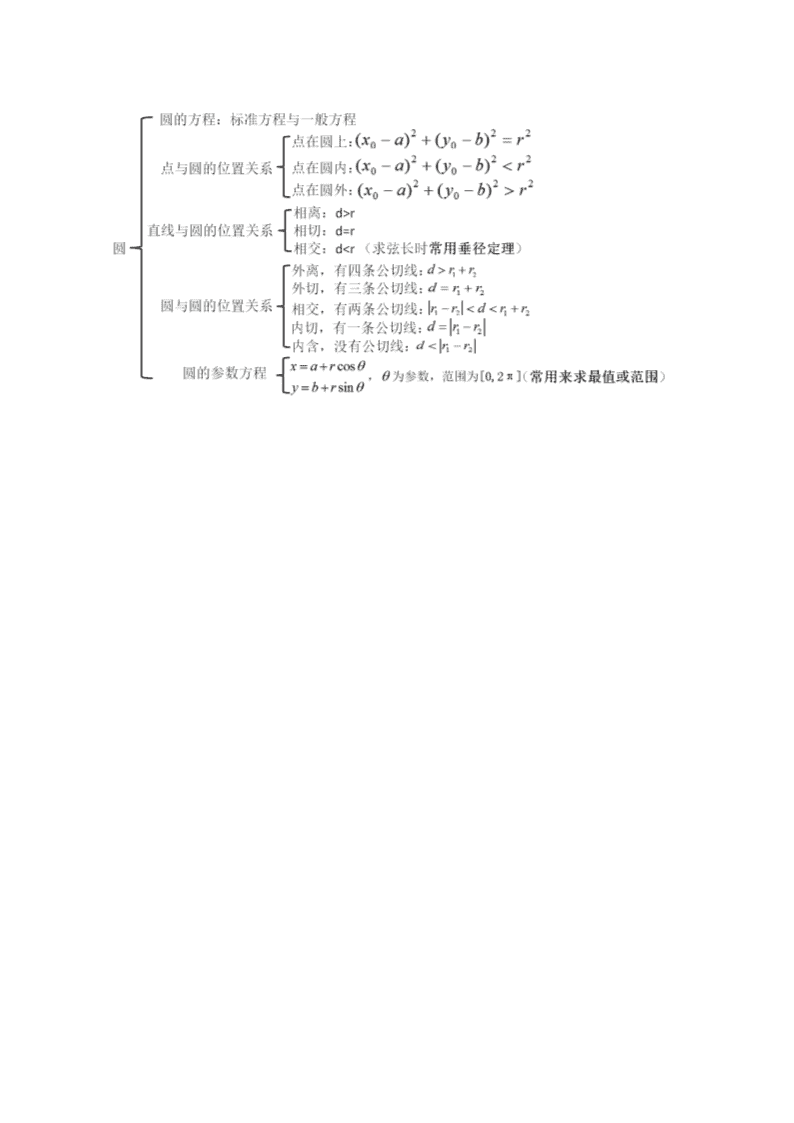
高考数学直线和圆的方程专题复习专题训练
专题六、解析几何(一) 直线和圆 1.直线方程: 2.点关于特殊直线的对称点坐标: (1)点关于直线方程的对称点坐标为:,; (2) 点关于直线方程的对称点坐标为:,; (3)点关于直线方程的对称点坐标为:,; (4)点关于直线方程的对称点坐标为:,; 3.圆的方程:或,无xy。 4.直线与圆相交: (1)利用垂径定理和勾股定理求弦长: 弦长公式:(为圆心到直线的距离),该公式只适合于圆的弦长。 若直线方程和圆的方程联立后,化简为:,其判别式为,则 弦长公式(万能公式): 注意:不需要单独把直线和圆的两个交点的坐标求出来来求弦长,只要设出它们的坐标即可,再利用直线方程和圆的联立方程求解就可达到目标。这是一种“设而不求”的技巧,它可以简化运算,降低思考难度,在解析几何中具有十分广泛的应用。 5.圆的切线方程: (1)点在圆外: 如定点,圆:,[] 第一步:设切线方程;第二步:通过,求出k,从而得到切线方程,这里的切线方程的有两条。特别注意:当不存在时,要单独讨论。 (2)点在圆上: 若点P在圆上,利用点法向量式方程求法,则切线方程为:。 点在圆上时,过点的切线方程的只有一条。 由(1)(2)分析可知:过一定点求某圆的切线方程,要先判断点与圆的位置关系。 (3)若点P在圆外,即, 过点P的两条切线与圆相交于A、B两点,则AB两点的直线方程为:。 6.两圆公共弦所在直线方程: 圆:,圆:, 则为两相交圆公共弦方程。 7.圆的对称问题: (1)圆自身关于直线对称:圆心在这条直线上。 (2)圆C1关于直线对称的圆C2:两圆圆心关于直线对称,且半径相等。 (3)圆自身关于点P对称:点P就是圆心。 (4)圆C1关于点P对称的圆C2:两圆圆心关于点P对称,且半径相等。 例1.已知直线中的 a,b,c 是取自集合{﹣3,﹣2,﹣1,0,1,2,3}中的3个不同的元素,并且该直线的倾斜角为锐角,则这样的直线共有_______条。 例2.已知圆C:,直线: (Ⅰ)求直线被圆C所截得的弦长最短时m的值及最短弦长; (Ⅱ)已知坐标轴上点A(0,2)和点T(t,0)满足:存在圆C上的两点P和Q,使得,求实数t的取值范围. 变式训练: 1.直线的倾斜角的取值范围是____________ 2.若表示两条直线,则实数=__________ 3.若点A(1,0)和点B(4,0)到直线l的距离依次为1和2,则这样的直线有____条。 4.直线过P(1,2),且A(2,3),B(4,﹣5)到的距离相等,则直线的方程是_________________ 5.若直线1:与2:平行,则实数a的值为________ 6.过点P(3,0)有一条直线,它夹在两条直线1:2x﹣y﹣2=0与2:x+y+3=0之间的线段恰被点P平分,则直线方程为____________________ 7.过点(5,2),且在x轴上的截距是在y轴上的截距的2倍的直线方程是__________________ 8.(2007湖北)已知直线(是非零常数)与圆有公共点,且 公共点的横坐标和纵坐标均为整数,那么这样的直线共有_______________条。 9.数学家欧拉在1765年提出定理:三角形的外心、重心、垂心依次位于同一直线上,且重心到外心的距离是重心到垂心距离的一半,这条直线被后人称之为三角形的欧拉线.若△ABC的顶点A(2,0),B(0,4),且△ABC的欧拉线的方程为,则顶点C的坐标为( ) A.(﹣4,0) B.(﹣4,﹣2) C.(﹣2,2) D.(﹣3,0) 10.已知直线过点,且与直线的夹角为, 直线的方程为_________________________ 11.已知的三个顶点为, 则的平分线所在直线的方程为________________ 12.若点P(m﹣2,n+1),Q(n,m﹣1)关于直线对称,则直线的方程是__________________ 13.直线x-y-2=0关于直线x+y+1=0对称的直线方程__________________ 14.(2012全国)正方形ABCD的边长为1,点E在边AB上,点F在边BC上,AE=BF=,动点P从E出发沿直线向F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角,当点P第一次碰到E时,P与正方形的边碰撞的次数为( ) A.16 B.14 C.12 D.10 15.如图,点A、B、C的坐标分别为(0,2),(﹣2,0),(2,0),点M是边AB上异于A、B的一点,光线从点M出发,经BC,CA反射后又回到起点M.若光线NT交y轴于点(0,),则点M的坐标为______________ 16.(2016金山区一模)已知点P、Q分别为函数和图像上的点,则点P和Q两点距离的最小值为____________ 17.在Rt△ABC中,AB=2,AC=4,∠A为直角,P为AB中点,M、N分别是BC,AC上任一点,则△MNP周长的最小值是____________ 18.直线所经过的定点坐标为_________ 19.曲线C1:|与曲线C2:|所围成的图形面积为_________ 20.点P在△ABC内部(包含边界),|AC|=3,|AB|=4,|BC|=5,点P到三边的距离分别是d1,d2,d3,则d1+d2+d3的取值范围是____________ 21.已知P是以F1,F2为焦点的椭圆上一点,过焦点F2作∠F1PF2外角平分线的垂线,垂足为M,则点M的轨迹是( ) A.椭圆 B.圆 C.双曲线 D.双曲线的一支 22.已知圆C满足:①截y轴所得的弦长为2;②被x轴分成两段圆弧,其弧长的比为3:1;③圆心到直线l:x﹣2y=0的距离为;则圆C的方程为______________________ 23.设集合A={},则集合A所表示图形的面积为___________ 24.已知圆C:,直线:圆上存在两点到直线的距离为1,则的取值范围是___________ 25.已知a≠b,且,,则连接两点(a,a2),(b,b2)的直线与圆心在坐标原点的单位圆的位置关系是( ) A.相离 B.相切 C.相交 D.不能确定 26.已知圆C:,点P为直线:上的一动点,若在圆C上存在点M使得∠MPC=30°,则点P横坐标的取值范围________________ 27.已知⊙O1:与⊙O2:,则两圆公切线的方程为________ 28.过圆外一点,作这个圆的两条切线、,切点分别是、,则直线的方程为_______________ 29.圆C的方程为,圆M的方程为,过圆M上任意一点P作圆C的两条切线PE、PF,切点分别为E、F, 则的最小值为________________ 30.设为圆上的任一点,欲使不等式恒成立,则的取值范围是____________ 31.(2005江西)如图,设抛物线C:y=x2的焦点为F,动点P在直线l:x﹣y﹣2=0上运动,过P作抛物线C的两条切线PA、PB,且与抛物线C分别相切于A、B两点. (1)求△APB的重心G的轨迹方程; (2)证明:∠PFA=∠PFB. 32.如图,过点A作直线,交圆M:于点B、C,在BC上取一点P,使P点满足,. (1)求动点P的轨迹方程; (2)若点P的轨迹交圆M于点R、S,求△MRS面积的最大值.查看更多