立体几何高考题

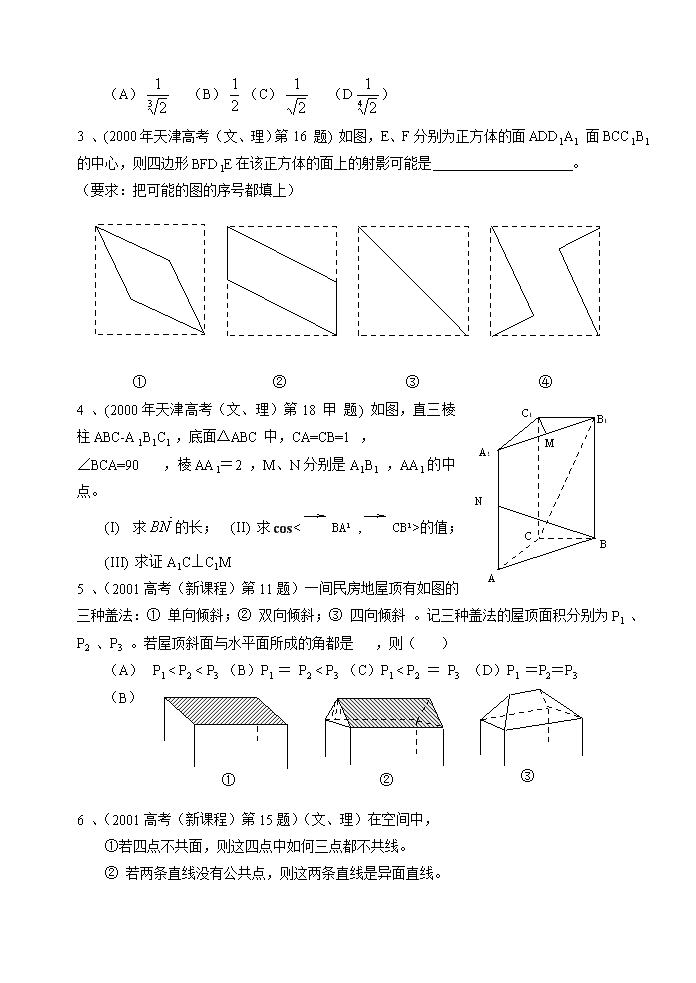
立体几何高考题

新教材高考研究 高二中心组 ‎ 第九章 立体几何 一、教材、考试要求的变化 旧教材考试说明中的“对于截面问题，只要求会解决与几种特殊的截面（棱柱、棱锥、棱台的对角面，棱柱的直截面，圆柱、圆锥、圆台的轴截面和平行于底面的截面，球的截面）以及已给出图形或它的全部顶点的其他截面的有关问题．” 提法删去了，而增加了“了解正多面体的概念，了解多面体的欧拉公式。”最主要的是增加了空间向量的运算以及在距离、夹角等的应用。具体如下：‎ ‎9．（B）直线、平面、简单几何体 考试内容 平面及其基本性质，平面图形直观图的画法 平行直线 直线的方向向量，异面直线所成的角，异面直线的公垂线，异面直线的距离 直线和平面垂直的性质，平面的法向量，点到平面的距离，直线和平面所成的角，向量在平面内的射影 平行平面的判定和性质，平行平面间的距离，二面角及其平面角，两个平面垂直的判定和性质 多面体、棱柱、棱锥、正多面体、球 考试要求 ‎（1）掌握平面的基本性质，会用斜二测的画法画水平放置的平面图形的直观图，能够画出空间两条直线、直线和平面的各种位置关系的图形，能够根据图形想象它们的位置关系。‎ ‎（2）了解空两条直线、直线和平面、两个平面的位置关系。‎ ‎（3）掌握直线和平面平行的判定定理和性质定理，理解直线和平面垂直的概念，掌握直线和平面垂直的判定定理，了解三垂线定理及其逆定理。‎ ‎（4）理解空间向量的概念，掌握空间向量的加法、减法和数乘。‎ ‎（5）了解空间向量的基本定理，理解空间向量坐标的概念，掌握空间向量的坐标运算。‎ ‎（6）掌握空间向量的数量积的定义及其性质，掌握用直角坐标计算空间向量数量积的公式，掌握空间两点间距离公式。‎ ‎（7）理解直线的方向向量、平面的法向量、向量在平面内的射影等概念。‎ ‎（8）掌握直线和直线、直线和平面，平面和平面所成的角、距离的概念，对于异面直线的距离，只要求会计算已给出公垂线或在坐标表示下的距离，掌握直线和平面垂直的性质定理，掌握两个平面平行、垂直的判定定理和性质定理。‎ ‎（9）了解多面体的概念，了解凸多面体的概念。‎ ‎（10）了解棱柱的概念，掌握棱柱的性质，会画直棱柱的直观图。‎ ‎（11）了解棱锥的概念，掌握正棱锥的性质，会画正棱锥的直观图。‎ ‎（12）了解正多面体的概念，了解多面体的欧拉公式。‎ ‎（13）了解球的概念，掌握球的性质，掌握球的表面积、体积公式。‎ ‎ 教材的最大变化是首次引入空间向量，并用这一工具去解决空间的平行垂直关系，以及求空间的“距离”、“角”，因此，要重点掌握“空间向量”（可看着平面向量的推广），突出其“工具性”。在实际应用中，要强化训练如何将空间问题坐标化（如何建立空间坐标系，并确定相关点的坐标，这里还需要具有相应的平几知识）这一数学思想。‎ 二、高考试题汇编 ‎1 、(2000年天津高考(文、理)第3 题)一个长方体共一顶点的三个面的面积分别是、、，这个长方体对角线的长是（ ）‎ ‎ （A）2 （B）3 （C） （D）6‎ ‎2 、(2000年天津高考（文、理）第9 题)一个圆柱的侧面展开图是一个正方形，这个圆柱的全面积与侧面积的比是（ ）‎ A B C D C1‎ F B1‎ A1‎ D1‎ E ‎ （A） （B） （C） （D）‎ ‎3 、(2000年天津高考（理）第12 题)如图OA是圆锥底面的中心O到母线的垂线，OA绕轴旋转一周所得曲面将圆锥分成体积相等的两部分，则母线与轴的夹角的余弦值为（ ）‎ ‎ （A） （B） （C） （D）‎ ‎3 、(2000年天津高考（文、理）第16 题) 如图，E、F分别为正方体的面ADD1A1 面BCC1B1的中心，则四边形BFD1E在该正方体的面上的射影可能是 。‎ ‎（要求：把可能的图的序号都填上）‎ A B N C A1‎ C1‎ B1‎ M ‎ ① ② ③ ④ ‎ ‎4 、(2000年天津高考（文、理）第18 甲 题) 如图，直三棱柱ABC-A1B1C1 ，底面△ABC中，CA=CB=1 ，‎ ‎∠BCA=90° ，棱AA1＝2 ，M、N分别是A1B1 ，AA1的中点。‎ ‎ (I) 求的长； (II) 求cos< ,>的值；‎ ‎(III) 求证A1C⊥C1M ‎5 、（2001高考（新课程）第11题）一间民房地屋顶有如图的三种盖法：① 单向倾斜；② 双向倾斜；③ 四向倾斜 。记三种盖法的屋顶面积分别为P1 、P2 、P3 。若屋顶斜面与水平面所成的角都是a ，则（ ）‎ ‎① ‎ ‎③ ‎ ‎② ‎ （A） P1 < P2 < P3 （B）P1 ＝ P2 < P3 （C）P1 < P2 ＝ P3 （D）P1 ＝P2＝P3‎ （B） ‎6 、（2001高考（新课程）第15题）（文、理）在空间中，‎ ‎ ①若四点不共面，则这四点中如何三点都不共线。‎ ‎② 若两条直线没有公共点，则这两条直线是异面直线。‎ A B C D V E O y z x 以上两个命题中，逆命题为真命题的是： （把符合要求的命题序号都填上）。‎ ‎7 、（2001高考（新课程）第20题 甲）如图，以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O－xyz，其中Ox∥BC ，Oy∥AB。E为VC的中点，正四棱锥底面边长为2a，高为h。‎ ‎ （I）求cos< ,> ；‎ ‎ （II）记面BCV为a ，面DCV为 b ,若∠BED是二面角a－VC－b 的平面角，求cos∠BED （理科为：求∠BED）‎ ‎8 、(2002年天津高考第3题)已知m、n为异面直线，m Ì 平面a ，n Ì 平面 b ，a ∩ b ＝l ，则l （ ）‎ ‎ （A）与m、n都相交 （B）与m、n中至少一条相交 ‎（C）与m、n都不相交 （D）至多与m、n中的一条相交 ‎9 、(2002年天津高考第7题)正六棱柱ABCDEF－A1B1C1D1E1F1 的底面边长为1 ，侧棱长为，则这个棱柱的侧面对角线E1D与BC1 所成的角是 A B C A1‎ B1‎ C1‎ ‎ （A）90° （B）60° （C）45° （D）30° ‎ ‎10 、(2002年天津高考第18题 甲) 如图，正三棱柱ABC-A1B1C1 ，底面边长为a ，侧棱长为a ‎ （I）建立适当的坐标系，并写出点A 、B、 A1、C1 的坐标；‎ ‎ （II）求AC1与侧面ABB1A1 所成的角。‎ B A C D P E F ‎11 、（1999年上海考题第20题）如图，在四棱锥P-ABCD中，底面ABCD是一直角梯形，∠BAD=90° ，AD∥BC，AB＝a ，AD＝2a ，且PA⊥底面ABCD ，PD与底面成30° 角，‎ ‎ （I）若AE⊥PD，E为垂足，求证BE⊥PD；‎ ‎（II）求异面直线AE与CD所成角的大小（用反三角函数表示）。‎ 证明：如图，以A为原点，AB、AD、AP所在直线为坐标系，建立空间直角坐标系，则点 A（0，0，0）、B（a，0，0）、C（a，a，0）、D（0，2a，0）。‎ ‎（1）∵PA⊥底面ABCD，∠PDA是PD与底面成的角，∴∠PDA ＝30° 过E作EF⊥AD，垂足为F，则AE＝a，AF＝，EF＝，AP＝‎ ‎∴E（0，，）、P（0，0，）.‎ ＝（－a，，）、＝（0，－2a，）.‎ ·＝（－a）·0 ＋·（－2a）＋· ＝0‎ ‎∴BE⊥PD ‎（2）由（1）可得＝（0，，）、＝（－a，a，0）‎ 设与所成的角为q 则 cosq ＝＝‎ ‎∴q ＝arccos，即异面直线AE与CD所成角的大小为arccos 三、教学建议 从近几年的高考来看，新教材的甲组题（即9(B)考题）比乙组题（即9(A)考题）和全国题都要好做，其实，用向量方法去解传统的立体几何也是有优势的，如2000年的高考立体几何题，普遍都认为较难，但如果用向量方法去解，就很简单了 ‎(2000年全国（理）第18题的向量解法）如图，已知平行六面体ABCD-A1B1C1D1的底面ABCD是菱形，且∠C1CB＝∠C1CD=∠BCD=60° .‎ A B C D A1‎ B1‎ C1‎ D1‎ ‎ (I)证明：C1C⊥BD ；‎ ‎ (II)假定CD＝2，C1C＝，记面C1BD为a ，面CBD为 b ，求二面角a－BD－b 的平面角的余弦值；‎ ‎ (III)的值为多大时，能够使 A1C⊥平面C1BD ? 请给出证明。‎ (I) 证明：设＝ ＝ ＝，且||＝||‎ 由题知＝－＝－ ‎∵·＝||·||·cos60° ，‎ ·＝||·||·cos60° ，‎ ·＝－·(－)＝－·＋·＝0‎ ‎∴⊥ 即 C1C⊥BD ‎（II）由题知 | |＝||＝2，||＝||＝， 连结AC交BD于O，连C1O，则C1 D＝C1 B ∴C1O⊥C1 B ∴∠C1 OC为所求二面角的平面角。‎ ‎∵＝－＝－＝( ＋)－ ‎ ＝( ＋)‎ ‎∴·＝[( ＋)－]·( ＋)‎ ‎＝2 ＋·＋·＋2 －·－·＝‎ 而| |＝ ， | |＝| －| ＝ ‎ 二面角a－BD－b 的平面角的余弦值为 。‎ ‎（III）要使A1C⊥平面C1BD ，即使A1C⊥BD 或A1C⊥C1D来观察的值为多少。‎ ‎ 由假设有·＝0， ……………………① ‎ ‎ ·＝0. ……………………② ‎ ‎ 由题设有＝＋＝＋＋＝＋＋ ‎ ＝－＝－ ‎ ＝－＝－ ‎∵·＝(＋＋)·(－) ＝0 （∵||＝||）‎ ‎∴⊥这说明① 成立 又∵·＝(＋＋)·(－)‎ ‎ ＝·－·＋2 －·＋·－2 ‎ ‎ ＝||2 －||·|| －||2 ‎ 要⊥只要·＝0‎ ‎ 即||2 －||·||－||2 ＝0 解得||＝||‎ 即当||＝|| 时⊥ 由此可知＝＝＝1时，能使A1C⊥平面C1BD 再看2002广东高考第19题的向量解法：‎ ‎（II）证法一：‎ 不论棱锥的高如何变化，△PAD≌△PCD.‎ ‎ 作AE⊥DP ，垂足为E，连EC，则△ADE≌△CDE ，‎ ‎∴AE=CE，∠CED＝90° ‎ ‎∴∠CEA是面PAD与面PCD所成的二面角的平面角。‎ 设＝，＝，＝ 依题意得 ||＝|| ，⊥，＝－，＝－ 在Rt△CED中，cos<，>＝cos<，>＝ ，‎ ‎∴·＝（－）·（－）‎ ‎ ＝·－·－·＋|| 2 ＝－|| 2 < 0‎ ‎∴cos∠CEA < 0‎ ‎∴面PAD与面PCD所成的二面角恒大于90° ‎ 证法二：作AE⊥DP ，垂足为E，连EC，则△ADE≌△CDE ，‎ D C A P O E y x B ‎∴AE=CE，∠CED＝90° ‎ ‎∴∠CEA是面PAD与面PCD所成的二面角的平面角。且PD⊥面CEA ，PD⊥OE 设CA 、BD交于O，以CA所在直线为x轴，OE所在直线为y轴，建立平面直角坐标系，设PB＝x，在Rt△PBD中，∵OE⊥PD ‎∴OE＝‎ ‎∴C（，0）、A（，0）、E（0 ，）‎ ‎∴＝（，－），‎ ＝（，－）‎ ‎∴·＝‎ ‎∴cos∠CEA < 0‎ ‎∴面PAD与面PCD所成的二面角恒大于90° ‎ 从以上的解法可以看到，利用向量解立体几何问题，有其独特点优势，既可以将空间问题转化为研究某一平面的问题，用平面向量的方法（纯向量运算或坐标运算）去解决，还可以用空间向量的方法去解决。因此，教学中，不要用旧教材的方法去进行题形训练，着重在概念的理解和掌握（如二面角），向量工具的选择与操作，重视通性、通法的教学，提高教与学的效率。‎ ‎【2003上海（春季高考）19】 已知三棱柱ABC-A1B1C1，在某个空间直角坐标系中，＝ {，，0}，＝{m，0，0}，＝{0，0，n}，其中m、n > 0.‎ ‎ (1)证明：三棱柱ABC-A1B1C1是正三棱柱；‎ ‎ (2) 若m＝n，求直线CA1与平面A1ABB1所成角的大小。‎ 解答（1）∵＝－＝ {，，0}‎ ‎∴||＝m，‎ 又＝{，，0}，＝{m，0，0}，‎ ‎∴||＝m |，|＝m，‎ 即⊿ABC是正三角形。‎ 又•＝0，即⊥ 同理⊥，∴⊥平面ABC，从而三棱柱ABC-A1B1C1是正三棱柱；‎ ‎ （2）取AB的中点O，连结CO、A1O.‎ ‎ ∵CO⊥AB，平面ABC⊥平面ABB1A，‎ ‎∴CO⊥平面ABB1A，即∠CA1O为直线CA1与平面A1ABB1所成角，‎ 在Rt⊿CA1O中，CO＝，CA1＝‎ ‎∴sin∠CA1O＝‎ 即∠CA1O＝45°‎