- 2021-05-13 发布 |
- 37.5 KB |
- 6页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
1978年全国高考数学试题及其解析
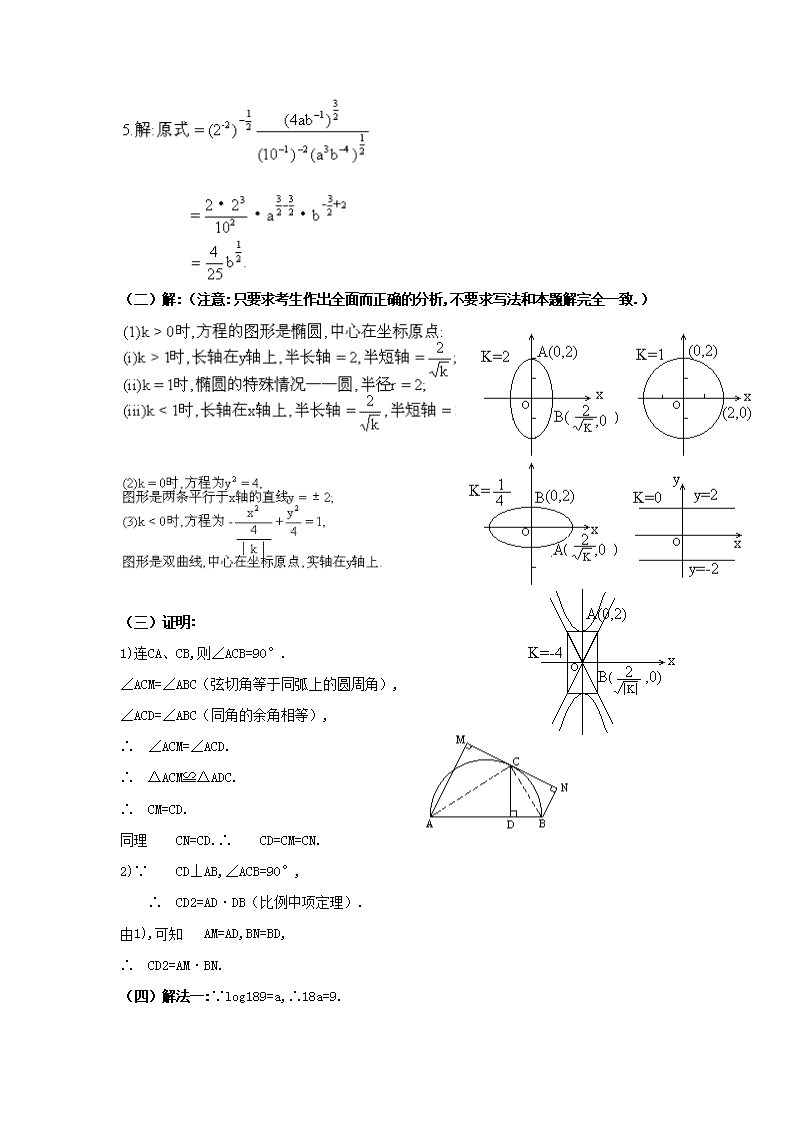
1978年全国高考数学试题及其解析 注意事项: 1.理工科考生要求除作(一)——(四)题和(七)题外,再由(五)、(六)两题中选作一题.文科考生要求作(一)——(四)题,再由(五)、(六)两题中选作一题;不要求作第(七)题. 2.考生解题作答时,不必抄题.但须准确地写明题号,例如(一)2、(五)等. (一)1.分解因式:x2-4xy+4y2-4z2. 2.已知正方形的边长为a.求侧面积等于这个正方形的面积、高等于这个正方形边长的直圆柱体的体积. (二)已知方程kx2+y2=4,其中k为实数.对于不同范围的k值,分别指出方程所代表图形的类型,并画出显示其数量特征的草图. (三)(如图)AB是半圆的直径,C是半圆上一点,直线MN切半圆于C点,AM⊥MN于M点,BN⊥MN于N点,CD⊥AB于D点. 求证:1)CD=CM=CN; 2)CD2=AM·BN. (四)已知log189=a(a≠2),18b=5.求log3645. (五)(本题和第(六)题选作一题)已知△ABC的三内角的大小成 (六)已知α、β为锐角,且3sin2α+2sin2β=1, 3sin2α-2sin2β=0. (七)(文科考生不要求作此题) 已知函数y=x2+(2m+1)x+m2-1(m为实数). (1)m是什么数值时,y的极值是0? (2)求证:不论m是什么数值,函数图象(即抛物线)的顶点都在同一条直线l1上.画出m=-1、0、1时抛物线的草图,来检验这个结论. (3)平行于l1的直线中,哪些与抛物线相交,哪些不相交?求证:任一条平行于l1而与抛物线相交的直线,被各抛物线截出的线段都相等. 试题答案及解析 (一)1.解:原式=(x2-4xy+4y2)-4z2 =(x-2y)2-(2z)2 =(x-2y-2z)(x-2y+2z). 2.解:设直圆柱体的底面半径为r.则底面周长2πr=a. 3.解:∵lg(2+x)≥0,∴2+x≥1. x≥-1为所求的定义域. (二)解:(注意:只要求考生作出全面而正确的分析,不要求写法和本题解完全一致.) (三)证明: 1)连CA、CB,则∠ACB=90°. ∠ACM=∠ABC(弦切角等于同弧上的圆周角), ∠ACD=∠ABC(同角的余角相等), ∴ ∠ACM=∠ACD. ∴ △ACM≌△ADC. ∴ CM=CD. 同理 CN=CD.∴ CD=CM=CN. 2)∵ CD⊥AB,∠ACB=90°, ∴ CD2=AD·DB(比例中项定理). 由1),可知 AM=AD,BN=BD, ∴ CD2=AM·BN. (四)解法一:∵log189=a,∴18a=9. 又 18b=5, ∴ 45=9×5=18a·18b=18a+b, 设 log3645=x,则36x=45=18a+b, ∴ log1836x=log1818a+b 但 36=2×18=4×9, ∴ log18(2×18)=log18(22×9). 即 1+log182=2log182+log189=2log182+a. ∴ log182=1-a. 以下解法同解法一. (五)解:A+B+C=180°, 又 2B=A+C. ∴ 3B=180°,B=60°,A+C=120°. 以下同证法一. (七)解:(1)用配方法得 此即各抛物线顶点坐标所满足的方程.它的图形是一条直线,方程中不 当m=-1、0、1时,x,y之间的函数关系为 分别作出它们的图象P1、P2、P3. 它们的顶点都在直线l1上. (3)设l:x-y=a为任一条平行于l1的直线. 与抛物线y=x2+(2m-1)x+m2-1方程联立求解. 消去y,得x2+2mx+m2-1+a=0. ∴ (x+m)2=1-a. 因而当1-a≥0即a≤1时,直线l与抛物线相交,而1-a<0即a>1时,直线l与抛物线不相交. 即直线l与抛物线两交点横坐标为 因直线l的斜率为1,它的倾斜角为45°. ∵ 直线l被抛物线截出的线段等于 而这与m无关. 因此直线l被各抛物线截出的线段都相等.查看更多