- 2021-05-13 发布 |
- 37.5 KB |
- 5页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考文科数学第一轮复习学案4
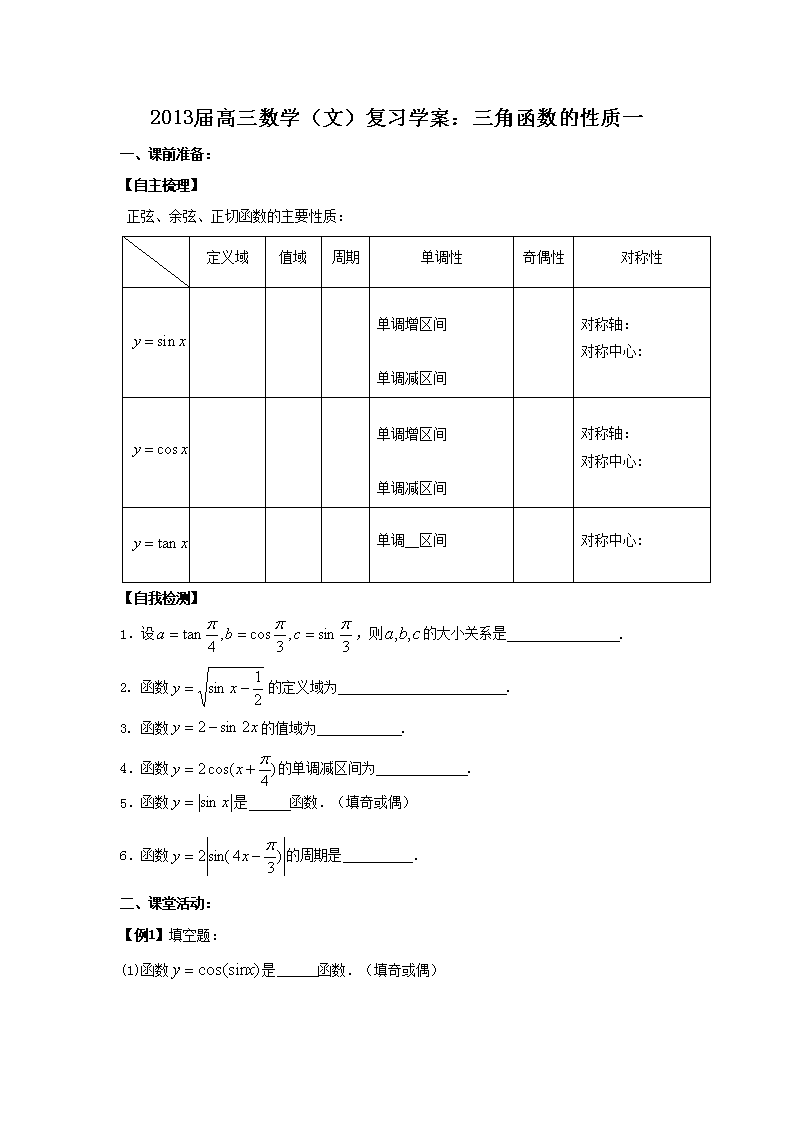
2013届高三数学(文)复习学案:三角函数的性质一 一、课前准备: 【自主梳理】 正弦、余弦、正切函数的主要性质: 定义域 值域 周期 单调性 奇偶性 对称性 单调增区间 单调减区间 对称轴: 对称中心: 单调增区间 单调减区间 对称轴: 对称中心: 单调 区间 对称中心: 【自我检测】 1.设,则的大小关系是 . 2. 函数的定义域为 . 3. 函数的值域为 . 4.函数的单调减区间为 . 5.函数是 函数.(填奇或偶) 6.函数的周期是 . 二、课堂活动: 【例1】填空题: (1)函数是 函数.(填奇或偶) (2)若函数在上单调递增,则正数的取值范围是________. (3)函数的周期为____________. (4)函数的图象和直线所围成的平面区域的面积是 . 【例2】已知函数. (1)求函数的最大值和最小值以及取最大、最小值时相应的取值集合; (2)写出函数的单调递增区间. 【例3】已知函数的最大值为1,最小值是-3,试确定的单调减区间. 课堂小结:掌握三角函数的简单性质:定义域,值域,单调性,奇偶性,周期等. 三、课后作业: 1.将用“<”号连接得: _________. 2.函数的单调减区间为 . 3.已知函数(、是常数),且,则______. 4.函数的最大值为 . 5.若函数是偶函数,则. 6.函数的周期为__________. 7.方程的实根个数为 个. 8.关于函数有下列四个命题正确的是 . ①由,可得必是的整数倍; ②的表达式可改写为; ③的图象关于点对称; ④的图象关于直线对称. 9. 已知函数(),求: (1)函数的最大值及取得最大值时的x; (2)函数的单调减区间. 10. 已知函数 ⑴ 求它的定义域和值域; ⑵ 求它的单调增区间; ⑶ 判断它的奇偶性; ⑷ 判定它的周期性,如果是周期函数,求出它的最小正周期. 四、 纠错分析 错题卡 题 号 错 题 原 因 分 析 参考答案: 课前准备: 1. 2. 3. 4. 5.偶 6. 课堂活动: 【例1】(1)偶 (2) (3) (4) 【例2】解析:(1) 当时, 当时, (2) 【例3】解析:由题意可解得 ,减区间为 ,减区间为 课后作业: 1. 2. 3.3 4.4 5. 6.2 7.3 8.②③ 9. (1)当时取得最大值4 (2)单调减区间 10.(1)定义域 值域 (2)增区间 (3)非奇非偶函数 (4)查看更多