北京市各地市高考数学联考试题分类汇编立体几何

北京市各地市高考数学联考试题分类汇编立体几何

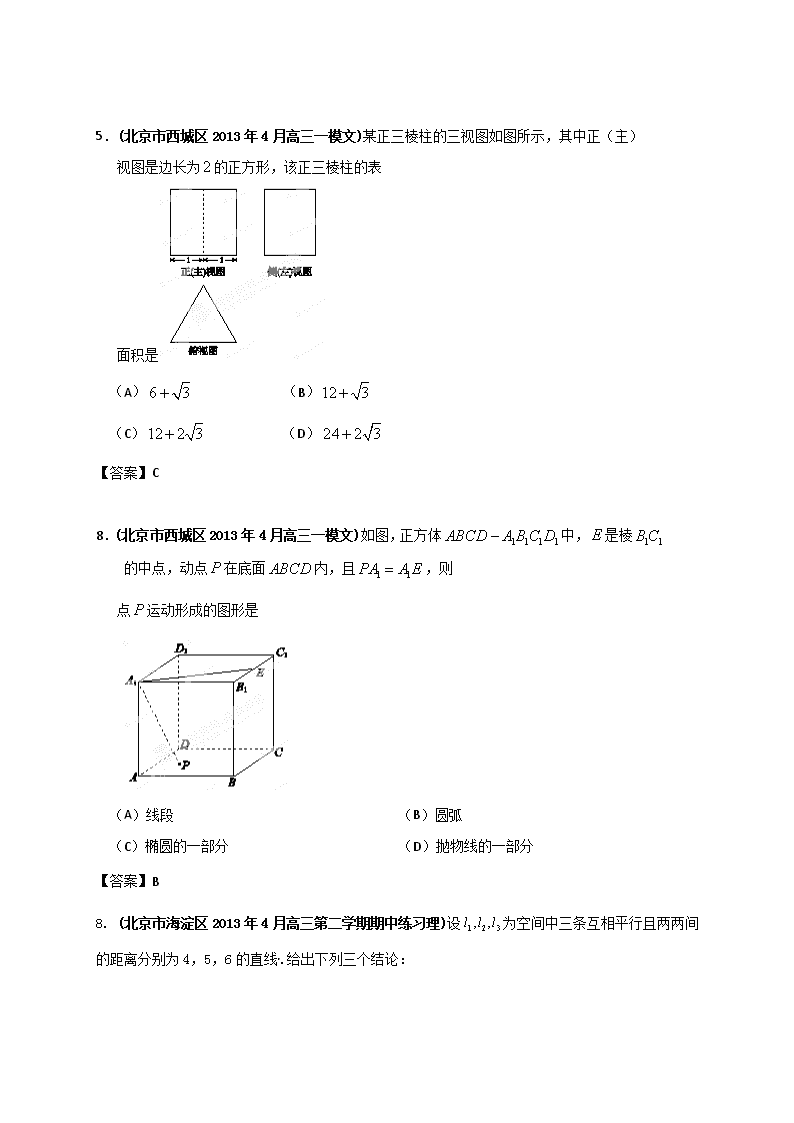
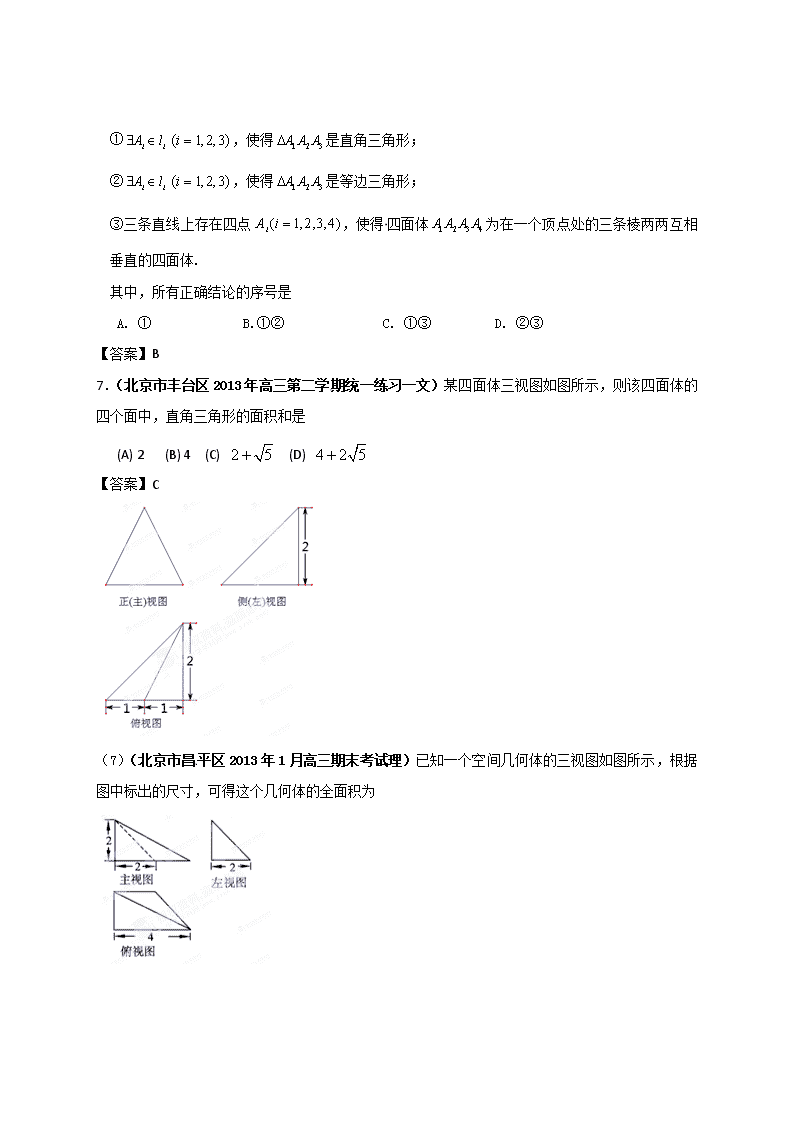
一、选择题:‎ ‎（6）(北京市朝阳区2013年4月高三第一次综合练习文理)某个长方体被一个平面所截，得到的几何体的三视图如图所示，则这个几何体的体积为 ‎ A. B. C. D. 8‎ ‎【答案】D ‎（5）(北京市东城区2013年4月高三综合练习一文）已知一个几何体的三视图如图所示(单位：cm)， 那么这个几何体的侧面积是 ‎（A） （B）‎ ‎（C） （D）‎ ‎【答案】C ‎7. (北京市房山区2013年4月高三第一次模拟理)某三棱椎的三视图如图所示，该三棱锥 的四个面的面积中，最大的是( C )‎ ‎ A. ‎ B. ‎ ‎ C. ‎ ‎ D. ‎ ‎5．(北京市西城区2013年4月高三一模文)某正三棱柱的三视图如图所示，其中正（主）‎ 视图是边长为的正方形，该正三棱柱的表 面积是 ‎（A） （B）‎ ‎（C） （D）‎ ‎【答案】C ‎8．(北京市西城区2013年4月高三一模文)如图，正方体中，是棱的中点，动点在底面内，且，则 点运动形成的图形是 ‎（A）线段 ‎（B）圆弧 ‎（C）椭圆的一部分 ‎（D）抛物线的一部分 ‎【答案】B ‎8. (北京市海淀区2013年4月高三第二学期期中练习理)设为空间中三条互相平行且两两间的距离分别为4，5，6的直线.给出下列三个结论：‎ ‎①，使得是直角三角形；‎ ‎②，使得是等边三角形；‎ ‎③三条直线上存在四点，使得四面体为在一个顶点处的三条棱两两互相垂直的四面体.‎ 其中，所有正确结论的序号是 A. ① B.①② C. ①③ D. ②③‎ ‎【答案】B ‎7．（北京市丰台区2013年高三第二学期统一练习一文）某四面体三视图如图所示，则该四面体的四个面中，直角三角形的面积和是 ‎(A) 2 (B) 4 (C) (D) ‎ ‎【答案】C ‎（7）（北京市昌平区2013年1月高三期末考试理）已知一个空间几何体的三视图如图所示，根据图中标出的尺寸，可得这个几何体的全面积为 ‎ ‎ ‎ A. B． C. D. ‎ 二、解答题:‎ ‎（17）(北京市朝阳区2013年4月高三第一次综合练习理)（本小题满分14分）[来源:学§科§网Z§X§X§K]‎ 如图，在四棱锥中，平面平面，且， ．四边形满足，，．点分别为侧棱上的点，且．‎ ‎（Ⅰ）求证：平面；‎ ‎（Ⅱ）当时，求异面直线与所成角的余弦值； ‎ ‎（Ⅲ）是否存在实数，使得平面平面？若存在，‎ 试求出的值；若不存在，请说明理由．‎ ‎（17）（本小题满分14分）‎ 证明：（Ⅰ）由已知，，‎ 所以 ． ‎ 所以 所以异面直线与所成角的余弦值为．…………………………………9分 ‎ ‎ ‎ 令，则．‎ 若平面平面，则，所以，解得．‎ 所以当时，平面平面．…………………………………………14分 ‎（17）(北京市朝阳区2013年4月高三第一次综合练习文) （本小题满分14分）‎ 如图，在四棱锥中，平面平面，且， ．四边形满足，，．为侧棱的中点，为侧棱上的任意一点.‎ ‎（Ⅰ）若为的中点，求证：平面；‎ ‎（Ⅱ）求证：平面平面； ‎ ‎（Ⅲ）是否存在点，使得直线与平面垂直？若存在，‎ 写出证明过程并求出线段的长；若不存在，请说明理由．[来源:学科网]‎ 平面平面，且，平面.‎ 所以平面，又平面，所以．‎ 又因为，，所以平面，‎ 而平面， ‎ 所以平面平面．……………………………………………………8分 可见直线与平面能够垂直，此时线段的长为．……………14分 ‎（16）(北京市东城区2013年4月高三综合练习一文）（本小题共14分）‎ A B C D E F 如图，已知平面，平面，为的中点，若 ‎．‎ ‎（Ⅰ）求证：平面；‎ ‎（Ⅱ）求证：平面平面．‎ ‎（16）（共14分）‎ A B C D E F G 证明：（Ⅰ）取的中点，连结，.‎ 因为是的中点，‎ 则为△的中位线．‎ 所以，． ‎ 因为平面，平面，‎ 所以．‎ 又平面，‎ 所以平面平面．‎ ‎16. (北京市房山区2013年4月高三第一次模拟理)（本小题满分14分）‎ 在四棱锥中，侧面⊥底面， [来源:学科网]‎ 为直角梯形，//，，‎ ‎，，为的中点．‎ ‎（Ⅰ）求证：PA//平面BEF；‎ ‎（Ⅱ）若PC与AB所成角为，求的长；‎ ‎（Ⅲ）在（Ⅱ）的条件下，求二面角F-BE-A的余弦值．‎ 解得： …………………………………………………………………….9分 解法二：由BCDE为正方形可得 ‎ 由ABCE为平行四边形 可得 //‎ 为 即…………………………………..…5分 ‎ ‎ 由图可知二面角的平面角是钝角， ‎ 所以二面角的余弦值为．………………………………………….14分 ‎16．(北京市西城区2013年4月高三一模文)（本小题满分14分）‎ 在如图所示的几何体中，面为正方形，面为等腰梯形，//，，，． [来源:学科网ZXXK]‎ ‎（Ⅰ）求证：平面；‎ ‎（Ⅱ）求四面体的体积； ‎ ‎（Ⅲ）线段上是否存在点，使//平面？‎ 证明你的结论．‎ ‎16．（本小题满分14分）‎ 因为 为正方形，所以为中点． ………………11分 ‎ 所以 //． ………………12分 因为 平面，平面， ………………13分 ‎ 所以 //平面．‎ 所以线段上存在点，使得//平面成立． ………………14分 ‎17. (北京市海淀区2013年4月高三第二学期期中练习理)（本小题满分14分）‎ 在四棱锥中，平面，是正三角形，与的交点恰好是中点，又，，点在线段上，且．‎ ‎（Ⅰ）求证：；‎ ‎（Ⅱ）求证：平面;‎ ‎（Ⅲ）求二面角的余弦值．‎ ‎………………9分 所以二面角余弦值为………………14分 ‎16．（北京市丰台区2013年高三第二学期统一练习一文） （本题13分）如图，四棱锥P-ABCD中， BC∥AD，BC=1，AD=3，AC⊥CD,且平面PCD⊥平面ABCD.‎ ‎（Ⅰ）求证：AC⊥PD；‎ ‎（Ⅱ）在线段PA上,是否存在点E，使BE∥平面PCD？若存在，求的值；若不存在，请说明理由。‎ 解：（Ⅰ）∵平面PCD⊥平面ABCD，平面PCD∩平面ABCD=CD, AC⊥CD , AC⊂平面ABCD ,‎ ‎∴AC⊥平面PCD, ...........................4分 ‎∵PD⊂平面PCD ,‎ ‎16．（北京市丰台区2013年高三第二学期统一练习一理）（本题14分）如图，四边形ABCD是边长为2的正方形，MD⊥平面ABCD，NB∥MD，且，MD=2；‎ ‎（Ⅰ）求证：AM∥平面BCN;‎ ‎（Ⅱ）求AN与平面MNC所成角的正弦值；‎ ‎（Ⅲ）E为直线MN上一点，且平面ADE⊥平面MNC，求的值.‎ ‎∵AM平面AMD,‎ ‎∴AM∥平面BCN…………………………………………………………………………………………4分 ‎(也可建立直角坐标系，证明AM垂直平面BCN的法向量，酌情给分)‎ 欲使平面ADE⊥平面MNC，只要，‎ ‎，，‎ ‎ . ………………………………………………………………………………14分 ‎ (16) （北京市昌平区2013年1月高三期末考试理）（本小题满分14分）在四棱锥中，底面是正方形，为的中点. （Ⅰ）求证：∥平面；‎ ‎（Ⅱ）求证：；‎ ‎（Ⅲ）若在线段上是否存在点，使？若存在，求出的值，若不存在，请说明理由．‎ ‎（16）(本小题满分14分)‎ ‎ ‎ ‎(III)解法一：‎ ‎ 在线段上存在点，使. 理由如下：‎ ‎ ‎ ‎ 解法二：‎ 由题意，若线段上存在点，使，则，.‎ 所以，，‎ 故在线段上存在点，使，且…………………… 14分