- 2021-05-13 发布 |
- 37.5 KB |
- 5页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考数学时复习题17
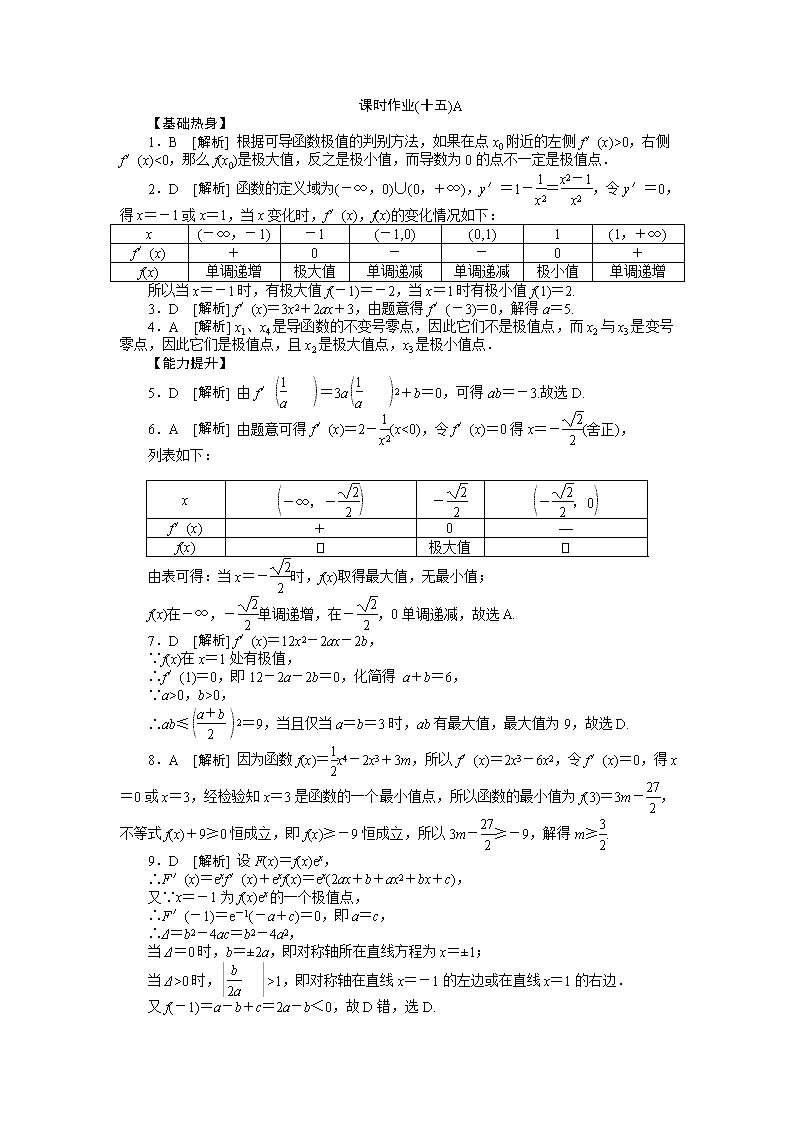
课时作业(十五)A [第15讲 导数与函数的极值、最值] [时间:45分钟 分值:100分] 1.下列命题中正确的是( ) A.导数为0的点一定是极值点 B.如果在点x0附近的左侧f′(x)>0,右侧f′(x)<0且f′(x0)=0,那么f(x0)是极大值 C.如果在点x0附近的左侧f′(x)>0,右侧f′(x)<0且f′(x0)=0,那么f(x0)是极小值 D.如果在点x0附近的左侧f′(x)<0,右侧f′(x)>0且f′(x0)=0,那么f(x0)是最小值 2.函数y=x+的极值情况是( ) A.既无极小值,也无极大值 B.当x=1时,极小值为2,但无极大值 C.当x=-1时,极大值为-2,但无极小值 D.当x=1时,极小值为2,当x=-1时,极大值为-2 3.函数f(x)=x3+ax2+3x-9,已知f(x)在x=-3处取得极值,则a=( ) A.2 B.3 C.4 D.5 4.已知函数y=f(x)的导函数y=f′(x)的图象如图K15-1,则( ) 图K15-1 A.函数f(x)有1个极大值点,1个极小值点 B.函数f(x)有2个极大值点,2个极小值点 C.函数f(x)有3个极大值点,1个极小值点 D.函数f(x)有1个极大值点,3个极小值点 5.[2011·张家界二模] 函数f(x)=ax3+bx在x=处有极值,则ab的值为( ) A.2 B.-2 C.3 D.-3 6.设函数f(x)=2x+-1(x<0),则f(x)( ) A.有最大值 B.有最小值 C.是增函数 D.是减函数 7.[2011·福建卷] 若a>0,b>0,且函数f(x)=4x3-ax2-2bx+2在x=1处有极值,则ab的最大值等于( ) A.2 B.3 C.6 D.9 8.已知函数f(x)=x4-2x3+3m,x∈R,若f(x)+9≥0恒成立,则实数m的取值范围是( ) A.m≥ B.m> C.m≤ D.m< 9.[2011·浙江卷] 设函数f(x)=ax2+bx+c(a,b,c∈R),若x=-1为函数f(x)ex的一个极值点,则下列图象不可能为y=f(x)的图象是( ) 图K15-2 10.函数f(x)=x2-lnx的最小值为________. 11.[2012·长春模拟] 已知函数f(x)=x3+3mx2+nx+m2在x=-1时有极值0,则m+n=________. 12.已知函数y=f(x)=x3+3ax2+3bx+c在x=2处有极值,其图象在x=1处的切线平行于直线6x+2y+5=0,则f(x)的极大值与极小值之差为________. 13.已知函数f(x)=x3-bx2+c(b,c为常数).当x=2时,函数f(x)取得极值,若函数f(x)只有三个零点,则实数c的取值范围为________. 14.(10分)已知函数f(x)=x5+ax3+bx+1,仅当x=-1,x=1时取得极值,且极大值比极小值大4. (1)求a、b的值; (2)求f(x)的极大值和极小值. 15.(13分)已知f(x)=x3+bx2+cx+2. (1)若f(x)在x=1时有极值-1,求b、c的值; (2)在(1)的条件下,若函数y=f(x)的图象与函数y=k的图象恰有三个不同的交点,求实数k的取值范围. 16.(12分)已知函数f(x)=xlnx. (1)求f(x)的最小值; (2)若对所有x≥1都有f(x)≥ax-1成立,求实数a的取值范围. 课时作业(十五)A 【基础热身】 1.B [解析] 根据可导函数极值的判别方法,如果在点x0附近的左侧f′(x)>0,右侧f′(x)<0,那么f(x0)是极大值,反之是极小值,而导数为0的点不一定是极值点. 2.D [解析] 函数的定义域为(-∞,0)∪(0,+∞),y′=1-=,令y′=0,得x=-1或x=1,当x变化时,f′(x),f(x)的变化情况如下: x (-∞,-1) -1 (-1,0) (0,1) 1 (1,+∞) f′(x) + 0 - - 0 + f(x) 单调递增 极大值 单调递减 单调递减 极小值 单调递增 所以当x=-1时,有极大值f(-1)=-2,当x=1时有极小值f(1)=2. 3.D [解析] f′(x)=3x2+2ax+3,由题意得f′(-3)=0,解得a=5. 4.A [解析] x1、x4是导函数的不变号零点,因此它们不是极值点,而x2与x3是变号零点,因此它们是极值点,且x2是极大值点,x3是极小值点. 【能力提升】 5.D [解析] 由f′=3a2+b=0,可得ab=-3.故选D. 6.A [解析] 由题意可得f′(x)=2-(x<0),令f′(x)=0得x=-(舍正), 列表如下: x - f′(x) + 0 — f(x) 极大值 由表可得:当x=-时,f(x)取得最大值,无最小值; f(x)在-∞,-单调递增,在-,0单调递减,故选A. 7.D [解析] f′(x)=12x2-2ax-2b, ∵f(x)在x=1处有极值, ∴f′(1)=0,即12-2a-2b=0,化简得 a+b=6, ∵a>0,b>0, ∴ab≤2=9,当且仅当a=b=3时,ab有最大值,最大值为9,故选D. 8.A [解析] 因为函数f(x)=x4-2x3+3m,所以f′(x)=2x3-6x2,令f′(x)=0,得x=0或x=3,经检验知x=3是函数的一个最小值点,所以函数的最小值为f(3)=3m-,不等式f(x)+9≥0恒成立,即f(x)≥-9恒成立,所以3m-≥-9,解得m≥. 9.D [解析] 设F(x)=f(x)ex, ∴F′(x)=exf′(x)+exf(x)=ex(2ax+b+ax2+bx+c), 又∵x=-1为f(x)ex的一个极值点, ∴F′(-1)=e-1(-a+c)=0,即a=c, ∴Δ=b2-4ac=b2-4a2, 当Δ=0时,b=±2a,即对称轴所在直线方程为x=±1; 当Δ>0时,>1,即对称轴在直线x=-1的左边或在直线x=1的右边. 又f(-1)=a-b+c=2a-b<0,故D错,选D. 10. [解析] 由得x>1. 由得0查看更多