高考数学总复习113推理与证明但因为测试新人教B版

高考数学总复习113推理与证明但因为测试新人教B版

‎2013年高考数学总复习 11-3 推理与证明但因为测试 新人教B版 ‎1.(文)(2011·江西文，6)观察下列各式：72＝49,73＝343,74＝2401，…，则72011的末两位数字为(　　) ‎ A．01　 　 　 B．43　 　 　‎ C．07　 　 　 D．49‎ ‎[答案]　B ‎[解析]　75＝16807,76＝117649，又71＝07，观察可见7n(n∈N*)的末二位数字呈周期出现，且周期为4，‎ ‎∵2011＝502×4＋3，‎ ‎∴72011与73末两位数字相同，故选B.‎ ‎(理)(2011·山东济宁一模)已知函数f(x)＝sinx＋ex＋x2010，令f1(x)＝f ′(x)，f2(x)＝f1′(x)，f3(x)＝f2′(x)，…，fn＋1(x)＝fn′(x)，则f2011(x)＝(　　)‎ A．sinx＋ex　　　 　　　　 B．cosx＋ex C．－sinx＋ex D．－cosx＋ex ‎[答案]　D ‎[解析]　f1(x)＝f ′(x)＝cosx＋ex＋2010x2009，‎ f2(x)＝f1′(x)＝－sinx＋ex＋2010×2009x2008，‎ f3(x)＝f2′(x)＝－cosx＋ex＋2010×2009×2008x2007，‎ f4(x)＝f3′(x)＝sinx＋ex＋2010×2009×2008×2007x2006，‎ 由此可以看出，该函数前2项的和成周期性变化，周期T＝4；‎ 而f2011(x)＝f ′2010(x)，此时其最后一项的导数将变为0.‎ 故求f2011(x)的值，只需研究该函数前2项和的变化规律即可，于是，f2011(x)＝f(3＋4×502)(x)＝－cosx＋ex.‎ ‎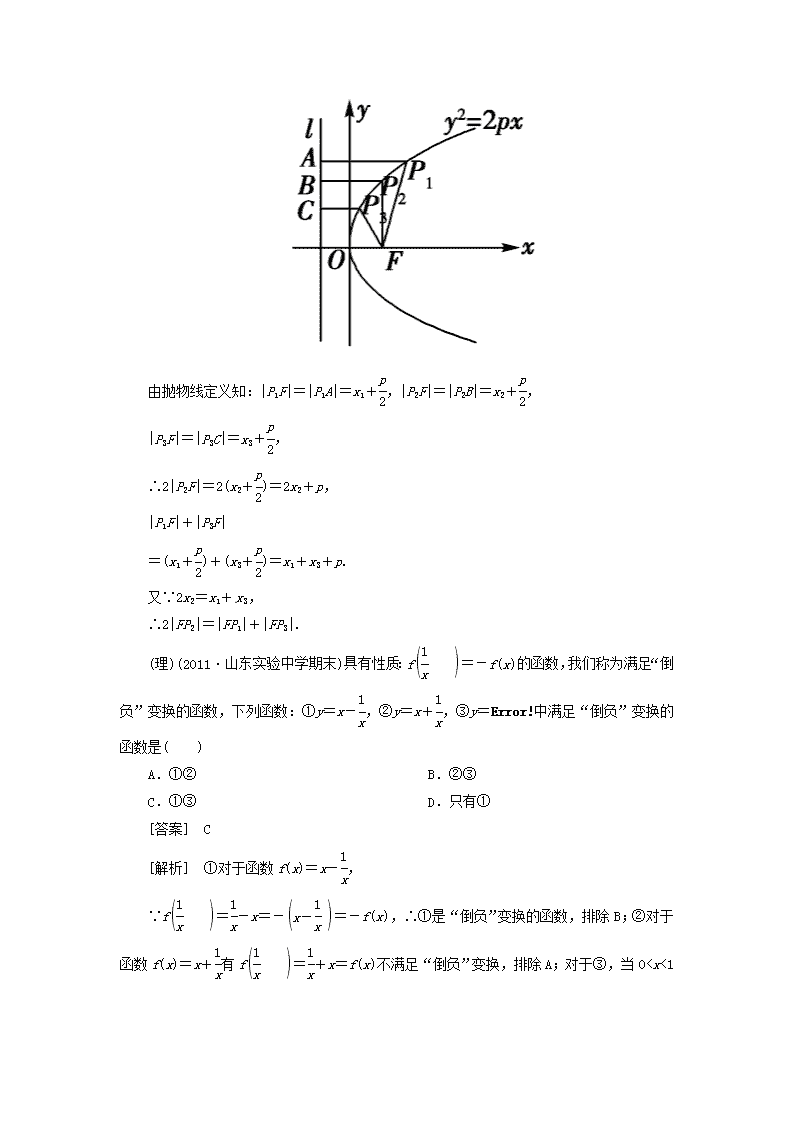2．(文)(2011·惠州模拟)已知抛物线y2＝2px(p>0)的焦点为F，点P1(x1，y1)、P2(x2，y2)、P3(x3，y3)在抛物线上，且2x2＝x1＋x3，则有(　　)‎ A．|FP1|＋|FP2|＝|FP3|‎ B．|FP1|2＋|FP2|2＝|FP3|2‎ C．2|FP2|＝|FP1|＋|FP3|‎ D．|FP2|2＝|FP1|·|FP3|‎ ‎[答案]　C ‎[解析]　如图所示，y2＝2px的准线为x＝－，P‎1A⊥l，P2B⊥l，P‎3C⊥l.‎ 由抛物线定义知：|P‎1F|＝|P‎1A|＝x1＋，|P‎2F|＝|P2B|＝x2＋，‎ ‎|P‎3F|＝|P‎3C|＝x3＋，‎ ‎∴2|P‎2F|＝2(x2＋)＝2x2＋p，‎ ‎|P‎1F|＋|P‎3F|‎ ‎＝(x1＋)＋(x3＋)＝x1＋x3＋p.‎ 又∵2x2＝x1＋x3，‎ ‎∴2|FP2|＝|FP1|＋|FP3|.‎ ‎(理)(2011·山东实验中学期末)具有性质：f＝－f(x)的函数，我们称为满足“倒负”变换的函数，下列函数：①y＝x－，②y＝x＋，③y＝中满足“倒负”变换的函数是(　　)‎ A．①② B．②③‎ C．①③ D．只有① ‎ ‎[答案]　C ‎[解析]　①对于函数f(x)＝x－，‎ ‎∵f＝－x＝－＝－f(x)，∴①是“倒负”变换的函数，排除B；②对于函数f(x)＝x＋有f＝＋x＝f(x)不满足“倒负”变换，排除A；对于③，当01，‎ ‎∵f(x)＝x，∴f＝＝－＝－f(x)；‎ 当x>1时，0<<1，∵f(x)＝－，‎ ‎∴f＝－x＝－f(x)；当x＝1时，＝1，‎ ‎∵f(x)＝0，∴f＝f(1)＝0＝－f(x)，‎ ‎∴③是满足“倒负”变换的函数，故选C.‎ ‎3.(2010·山东淄博一中)如图，在梯形ABCD中，AB∥DC，AB＝a，CD＝b(a>b)．若EF∥AB，EF到CD与AB的距离之比为mn，则可推算出：EF＝，试用类比的方法，推想出下述问题的结果．在上面的梯形ABCD中，延长梯形两腰AD、BC相交于O点，设△OAB、△OCD的面积分别为S1、S2，EF∥AB，且EF到CD与AB的距离之比为mn，则△OEF的面积S0与S1、S2的关系是(　　)‎ A．S0＝ B．S0＝ C.＝ D.＝ ‎[答案]　C ‎[解析]　根据面积比等于相似比的平方求解．‎ ‎4．(文)(2011·绍兴月考)古希腊人常用小石头在沙滩上摆成各种形状来研究数．比如： ‎ 他们研究过图1中的1,3,6,10，…，由于这些数能够表示成三角形，将其称为三角形数；类似的，称图2中的1,4,9,16，…这样的数为正方形数．下列数中既是三角形数又是正方形数的是(　　)‎ A．289 B．1024‎ C．1225 D．1378‎ ‎[答案]　C ‎[解析]　将三角形数记作an，正方形数记作bn，则an＝1＋2＋…＋n＝，bn＝n2，‎ 由于1225＝352＝，故选C.‎ ‎(理)(2011·咸阳市高考模拟考试)古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”，而把1,4,9,16…这样的数称为“正方形数”．如图，可以发现，任何一个大于1的“正方形数”都可以看作两个相邻的“三角形数”之和，下列等式中，符合这一规律的表达式是(　　)‎ ‎①13＝3＋10；②25＝9＋16；③36＝15＋21；④49＝18＋31；⑤64＝28＋36.‎ A．①④ B．②⑤‎ C．③⑤ D．②③‎ ‎[答案]　C ‎[解析]　这些“三角形数”依次是1,3,6,10,15,21,28,36,45，…且“正方形数”是“三角形数”中相邻两数之和，很容易得到：15＋21＝36,28＋36＝64，只有③⑤是对的．‎ ‎5．设⊕是R上的一个运算，A是R的非空子集，若对任意a、b∈A ，有a⊕b∈A，则称A对运算⊕封闭，下列数集对加法、减法、乘法和除法(除数不等于零)四则运算都封闭的是(　　)‎ A．自然数集 B．整数集 C．有理数集 D．无理数集 ‎[答案]　C ‎[解析]　令a＝1，b＝2，＝，可排除A、B.‎ 令a＝，b＝3，＝3，可排除D，故选C.‎ ‎[点评]　这是一个信息给予题，用筛选法(即排除法解)更加简便．‎ ‎6．(2011·长春十一中月考)规定一机器狗每秒钟只能前进或后退一步，现程序设计师让机器狗以“前进3步，然后再退2步”的规律移动．如果将此机器狗放在数轴原点，面向正方向，以1步的距离为1个单位长度移动，令P(n)表示第n秒时机器狗所在的位置坐标，且P(0)＝0，则下列结论中错误的是(　　)‎ A．P(2007)＝403 B．P(2008)＝404‎ C．P(2009)＝403 D．P(2010)＝404‎ ‎[答案]　D ‎[解析]　显然每5秒前进一个单位，且P(1)＝1，P(2)＝2，P(3)＝3，P(4)＝2，P(5)＝1，‎ ‎∴P(2007)＝P(5×401＋2)＝401＋2＝403，‎ P(2008)＝404，P(2009)＝403，P(2010)＝402，故选D.‎ ‎7．已知整数对排列如下：(1,1)，(1,2)，(2,1)，(1,3)，(2,2)，(3,1)，(1,4)，(2,3)，(3,2)，(4,1)，(1,5)，(2,4)，(3,3)，…，按以上构造规律，第60个数对是________．‎ ‎[答案]　(5,7)‎ ‎[解析]　所给各数对依次为对整数2,3,4,5，…的分解，且是第一个数从小到大依次分解，2的分解有一个(1,1)，3的分解有两个(1,2)，(2,1)，4的分解有(1,3)，(2,2)，(3,1)，n(n≥2，n∈N)的分解有n－1个，由≤60得，n≤11，‎ ‎∵n＝11时，＝55，故第60个数对为12的分解第5对，由(1,11)，(2,10)，(3,9)，(4,8)，(5,7)(或5＋7＝12)知，第5对为(5,7)．‎ ‎8．(2011·湘潭五模、蚌埠质检)已知＝2，＝3，＝4，…，若＝6，(a，t均为正实数)，类比以上等式，可推测a，t的值，则a＋t＝________.‎ ‎[答案]　41‎ ‎[解析]　根据题中所列的前几项的规律可知其通项应为＝n，所以当n＝6时a＝6，t＝35，a＋t＝41.‎ ‎9．(2011·江西吉安期末)请阅读下列材料：若两个正实数a1，a2满足a＋a＝1，那么a1＋a2≤.证明：构造函数f(x)＝(x－a1)2＋(x－a2)2＝2x2－2(a1＋a2)x＋1.因为对一切实数x，恒有f(x)≥0，所以Δ≤0，从而得4(a1＋a2)2－8≤0，所以a1＋a2≤.类比上述结论，若n个正实数满足a＋a＋…＋a＝1，你能得到的结论为________．‎ ‎[答案]　a1＋a2＋…＋an≤(n∈N*)‎ ‎[解析]　构造函数f(x)＝(x－a1)2＋(x－a2)2＋…＋(x－an)2＝nx2－2(a1＋a2＋…＋an)x＋1，‎ ‎∵f(x)≥0对任意实数x都成立，‎ ‎∴Δ＝4(a1＋a2＋…＋an)2－4n≤0，‎ ‎∵a1，a2，…，an都是正数，∴a1＋a2＋…＋an≤.‎ ‎10．设{an}是公比为q的等比数列，Sn是它的前n项和．‎ ‎(1)求证：数列{Sn}不是等比数列；‎ ‎(2)数列{Sn}是等差数列吗？为什么？‎ ‎[解析]　(1)证明：法一(反证法)：若{Sn}是等比数列，则S＝S1S3，即 a(1＋q)2＝a1·a1(1＋q＋q2)．‎ ‎∵a1≠0，∴(1＋q)2＝1＋q＋q2，∴q＝0，与q≠0矛盾，故{Sn}不是等比数列．‎ 法二：只需证明SnSn＋2≠S.‎ ‎∵Sn＋1＝a1＋qSn，Sn＋2＝a1＋qSn＋1，‎ ‎∴SnSn＋2－S＝Sn(a1＋qSn＋1)－(a1＋qSn)Sn＋1＝a1(Sn－Sn＋1)＝－a1an＋1≠0.‎ 故{Sn}不是等比数列．‎ ‎(2)解：当q＝1时，{Sn}是等差数列．当q≠1时，{Sn}不是等差数列，否则由S1，S2，S3成等差数列得，2S2＝S1＋S3.‎ ‎∴‎2a1(1＋q)＝a1＋a1(1＋q＋q2)．由于a1≠0，‎ ‎∴2(1＋q)＝2＋q＋q2，q＝q2，‎ ‎∵q≠1，∴q＝0，与q≠0矛盾.‎ ‎11.下图为某三岔路口交通环岛的简化模型．在某高峰时段，单位时间进出路口A、B、C的机动车辆数如图所示，图中x1、x2、x3分别表示该时段单位时间通过路段、、的机动车辆数(假设：单位时间内，在上述路段中，同一路段上驶入与驶出的车辆数相等)，则(　　)‎ A．x1>x2>x3 B．x1>x3>x2‎ C．x2>x3>x1 D．x3>x2>x1‎ ‎[答案]　C ‎[解析]　∵x1＝50＋(x3－55)＝x3－5⇒x3>x1，‎ x2＝30＋(x1－20)＝x1＋10⇒x2>x1，‎ x3＝30＋(x2－35)＝x2－5⇒x2>x3，‎ ‎∴x2>x3>x1，∴选C.‎ ‎[点评]　抓住“同一路段上驶入与驶出的车辆数相等”这一信息是解题的关键，考查阅读理解能力．‎ ‎12．(文)(2011·泉州模拟)考察下列一组不等式：23＋53>22·5＋2·52,24＋54>23·5＋2·53,2＋5>22·5＋2·52，….将上述不等式在左右两端仍为两项和的情况下加以推广，使以上的不等式成为推广不等式的特例，则推广的不等式为________________________．‎ ‎[答案]　am＋n＋bm＋n>ambn＋anbm(a，b>0，a≠b，m，n>0)‎ ‎[解析]　由“23＋53>22·5＋2·‎52”‎，“24＋54>23·5＋2·‎53”‎，“2＋5>22·5＋2·‎5”‎，可得推广形式的最基本的印象：应具有“□□＋□□>□□·□□＋□□·□□”的形式．‎ 再分析底数间的关系，可得较细致的印象：应具有“a□＋b□>a□·b□＋a□·b□”的形式．‎ 再分析指数间的关系，可得准确的推广形式：am＋n＋bm＋n>ambn＋anbm(a，b>0，a≠b，m，n>0)．‎ ‎(理)观察等式：sin230°＋cos260°＋sin30°cos60°＝，sin220°＋cos250°＋sin20°cos50°＝和sin215°＋cos245°＋sin15°cos45°＝，…，由此得出以下推广命题，则推广不正确的是(　　)‎ A．sin2α＋cos2β＋sinαcosβ＝ B．sin2(α－30°)＋cos2α＋sin(α－30°)cosα＝ C．sin2(α－15°)＋cos2(α＋15°)＋sin(α－15°)cos(α＋15°)＝ D．sin2α＋cos2(α＋30°)＋sinαcos(α＋30°)＝ ‎[答案]　A ‎[解析]　观察已知等式不难发现，60°－30°＝50°－20°＝45°－15°＝30°，推广后的命题应具备此关系，但A中α与β无联系，从而推断错误的命题为A.选A.‎ ‎13．(文)(2011·江苏苏州测试、南宁模拟)已知结论：“在三边长都相等的△ABC中，若D是BC的中点，G是△ABC外接圆的圆心，则＝‎2”‎．若把该结论推广到空间，则有结论：“在六条棱长都相等的四面体ABCD中，若M是△BCD的三边中线的交点，O为四面体ABCD外接球的球心，则＝________.”‎ ‎[答案]　3‎ ‎[解析]　如图，易知球心O在线段AM上，不妨设四面体ABCD的边长为1，外接球的半径为R，则BM＝×＝，‎ ‎ ‎ AM＝＝，‎ R＝，解得R＝.‎ 于是，＝＝3.‎ ‎(理)如图所示，面积为S的平面凸四边形的第i条边的边长记为ai(i＝1,2,3,4)，此四边形内任一点P到第i条边的距离记为hi(i＝1,2,3,4)，若＝＝＝＝k，则(ihi)＝.类比以上性质，体积为V的三棱锥的第i个面的面积记为Si(i＝1,2,3,4)，此三棱锥内任一点Q到第i个面的距离记为Hi(i＝1,2,3,4)，若＝＝＝＝k，则(iHi)的值为(　　)‎ A. B. C. D. ‎[答案]　B ‎[解析]　在平面四边形中，连接P点与各个顶点，将其分成四个小三角形，根据三角形面积公式，得 S＝(a1h1＋a2h2＋a3h3＋a4h4)‎ ‎＝(kh1＋2kh2＋3kh3＋4kh4)＝(ihi)．‎ 所以(ihi)＝.‎ 类似地，连接Q点与三棱锥的四个顶点，将其分成四个小三棱锥，则有 V＝(S1H1＋S2H2＋S3H3＋S4H4)‎ ‎＝(kH1＋2kH2＋3kH3＋4kH4)‎ ‎＝(H1＋2H2＋3H3＋4H4)＝(iHi)，‎ ‎∴(iHi)＝.‎ ‎[点评]　类比推理是由特殊到特殊的推理，是两类相类似的对象之间的推理，类比的关键是能把两个系统之间的某种一致性(相似性)确切地表达出来，也就是要把相关对象在某些方面一致性的含糊认识说清楚．类比推理能够为我们提供发现的思路和方向，但类比推理的结论不一定正确．‎ ‎14．先解答(1)，再根据结构类比解答(2)：‎ ‎(1)已知a，b为实数，且|a|<1，|b|<1，求证：ab＋1>a＋b.‎ ‎(2)已知a，b，c均为实数，且|a|<1，|b|<1，|c|<1，求证：abc＋2>a＋b＋c.‎ ‎[解析]　(1)ab＋1－(a＋b)＝(a－1)(b－1)>0.‎ ‎(2)∵|a|<1，|b|<1，|c|<1，据(1)得(ab)·c＋1>ab＋c，‎ ‎∴abc＋2＝[(ab)·c＋1]＋1>(ab＋c)＋1＝(ab＋1)＋c>a＋b＋c.‎ 你能再用归纳推理方法猜想出更一般地结论吗？‎ 即xi∈R，|xi|<1(i＝1,2，…，n)时，有________．‎ ‎15．(2011·上海模拟)冬天，洁白的雪花飘落时非常漂亮．为研究雪花的形状，1904年，瑞典数学家科克(Koch Heige Von)把雪花理想化，得到了雪花曲线，也叫科克曲线．它的形成过程如下：‎ ‎(ⅰ)将正三角形(图①)的每边三等分，并以中间的那一条线段为一底边向形外作等边三角形，然后去掉底边，得到图②；‎ ‎(ⅱ)将图②的每三边等分，重复上述作图方法，得到图③；‎ ‎(ⅲ)再按上述方法无限多次继续作下去，所得到的曲线就是雪花曲线．‎ 将图①、图②、图③……中的图形依次记作M1，M2，…，Mn，…，设M1的边长为1. ‎ 记Mn的边数为an，边长bn，周长为Ln.‎ ‎(1)写出a1，a2，a3；b1，b2，b3；‎ ‎(2)求an，bn，Ln.‎ ‎[解析]　(1)a1＝3，a2＝12，a3＝48，b1＝1，b2＝，b3＝，‎ ‎(2)其边数与边长的变化规律是：一条边变为4条边，边长为原来的，如图∴an＋1＝4an，bn＋1＝bn.‎ 又a1＝3，∴an＝3×4n－1，‎ ‎∵b1＝1，∴bn＝.‎ ‎(3)Ln＝an·bn＝3×4n－1× ‎＝3·n－1.‎ ‎16．已知a>b>c，且a＋b＋c＝0，求证：0，‎ 只需证(a－b)(‎2a＋b)>0，只需证(a－b)(a－c)>0.‎ 因为a>b>c，所以a－b>0，a－c>0，‎ 所以(a－b)(a－c)>0，显然成立，故原不等式成立．‎ ‎1．设a、b、c∈R＋，P＝a＋b－c，Q＝b＋c－a，R＝c＋a－b，则“PQR>‎0”‎是“P、Q、R同时大于零”的(　　)‎ A．充分而不必要条件 B．必要而不充分条件 C．充要条件 D．既不充分也不必要条件 ‎[答案]　C ‎[解析]　首先若P、Q、R同时大于零，则必有PQR>0成立．‎ 其次，若PQR>0，且P、Q、R不都大于0，则必有两个为负，‎ 不妨设P<0，Q<0，即a＋b－c<0，b＋c－a<0，∴b<0与b∈R＋矛盾，故P、Q、R都大于0.‎ ‎2．将正整数排成下表：‎ 则在表中数字2010出现在(　　)‎ A．第44行第75列 B．第45行第75列 C．第44行第74列 D．第45行第74列 ‎[答案]　D ‎[解析]　第n行有2n－1个数字，前n行的数字个数为1＋3＋5＋…＋(2n－1)＝n2.∵442＝1936,452＝2025，且1936<2010,2025>2010，∴2010在第45行．‎ 又2025－2010＝15，且第45行有2×45－1＝89个数字，∴2010在第89－15＝74列，选D.‎ ‎3．(2011·清远模拟)定义A*B，B*C，C*D，D*A的运算分别对应图中的(1)(2)(3)(4)，那么下图中(A)(B)所对应的运算结果可能是(　　)‎ A．B*D，A*D B．B*D，A*C C．B*C，A*D D．C*D，A*D ‎[答案]　B ‎[解析]　观察图形及对应运算分析可知，基本元素为A→|，B→□，C→——，D→○，从而可知图(A)对应B*D，图B对应A*C.‎ ‎4．(2011·皖南八校联考)为提高信息在传输中的抗干扰能力，通常在原信息中按一定规则加入相关数据组成传输信息．设定原信息为a‎0a1a2，ai∈{0,1}(i＝0,1,2)，传输信息为h‎0a0a1a2h1，其中h0＝a0⊕a1，h1＝h0⊕a2，⊕运算规则为：0⊕0＝0,0⊕1＝1,1⊕0＝1,1⊕1＝0.例如原信息为111，则传输信息为01111，信息在传输过程中受到干扰可能导致接收信息出错，则下列接收信息一定有误的是(　　)‎ A．11010 B．01100‎ C．10111 D．00011‎ ‎[答案]　C ‎[解析]　对于选项C，传输信息是10111，对应的原信息是011，由题目中运算规则知h0＝0⊕1＝1，而h1＝h0⊕a2＝1⊕1＝0，故传输信息应是10110.‎ ‎5．n个连续自然数按规律排成下表：‎ 根据规律，从2008到2010的箭头方向依次为(　　)‎ A．↓→ B．→↑‎ C．↑→ D．→↓‎ ‎[答案]　A ‎[解析]　观察图例可见，位序相同的数字都是以4为公差的等差数列，故从2008至2010，其位序应与相同，故选A.‎ ‎6．(2010·曲师大附中)设△ABC的三边长分别为a、b、c，△ABC的面积为S，内切圆半径为r，则r＝；类比这个结论可知：四面体S－ABC的四个面的面积分别为S1、S2、S3、S4，内切球的半径为r，四面体S－ABC的体积为V，则r＝(　　)‎ A. B. C. D. ‎[答案]　C ‎[解析]　设三棱锥的内切球球心为O，那么由VS－ABC＝VO－ABC＋VO－SAB＋VO－SAC＋VO－SBC，‎ 即V＝S1r＋S2r＋S3r＋S4r，‎ 可得r＝.‎ ‎7．(2011·陕西文，13)观察下列等式 ‎　　　　　　　1＝1‎ ‎　　　　　　2＋3＋4＝9‎ ‎　　　　　3＋4＋5＋6＋7＝25‎ ‎　　　　4＋5＋6＋7＋8＋9＋10＝49‎ ‎　　　　　　　　　……‎ 照此规律，第五个等式应为______________________．‎ ‎[答案]　5＋6＋7＋8＋9＋10＋11＋12＋13＝81‎ ‎[解析]　第1个等式有1项，从1开始 第2个等式有3项，从2开始 第3个等式有5项，从3开始 第4个等式有7项，从4开始 每个等式左边都是相邻自然数的和，右边是项数的平方，故由已知4个等式的变化规律可知，第5个等式有9项，从5开始，等式右边是92，故为5＋6＋7＋8＋9＋10＋11＋12＋13＝81.‎ ‎[点评]　观察各等式特点可得出一般结论：n＋(n＋1)＋(n＋2)＋…＋(3n－2)＝(2n－1)2.‎ ‎8．(2011·台州模拟)观察下列等式：‎ ‎(1＋x＋x2)1＝1＋x＋x2，‎ ‎(1＋x＋x2)2＝1＋2x＋3x2＋2x3＋x4，‎ ‎(1＋x＋x2)3＝1＋3x＋6x2＋7x3＋6x4＋3x5＋x6，‎ ‎(1＋x＋x2)4＝1＋4x＋10x2＋16x3＋19x4＋16x5＋10x6＋4x7＋x8，‎ ‎……‎ 由以上等式推测：对于n∈N*，若(1＋x＋x2)n＝a0＋a1x＋a2x2＋…＋a2nx2n，则a2＝________.‎ ‎[答案]　n(n＋1)‎ ‎[解析]　由给出等式观察可知，x2的系数依次为1,3,6,10,15，…，∴a2＝n(n＋1)．‎ ‎9．(2011·盐城市高三第一次调研)观察下列几个三角恒等式：‎ ‎①tan10°tan20°＋tan20°tan60°＋tan60°tan10°＝1；‎ ‎②tan5°tan100°＋tan100°tan(－15°)＋tan(－15°)tan5°＝1；‎ ‎③tan13°tan35°＋tan35°tan42°＋tan42°tan13°＝1.‎ 一般地，若tanα，tanβ，tanγ都有意义，你从这三个恒等式中猜想得到的一个结论为__________________________．‎ ‎[答案]　当α＋β＋γ＝90°时，tanαtanβ＋tanβtanγ＋tanγtanα＝1‎ ‎[解析]　所给三角恒等式都为tanαtanβ＋tanβtanγ＋tanγtanα＝1的结构形式，且α，β，γ之间满足α＋β＋γ＝90°.‎