- 2021-05-13 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
一类平面磁聚焦模型在高考和竞赛中的应用
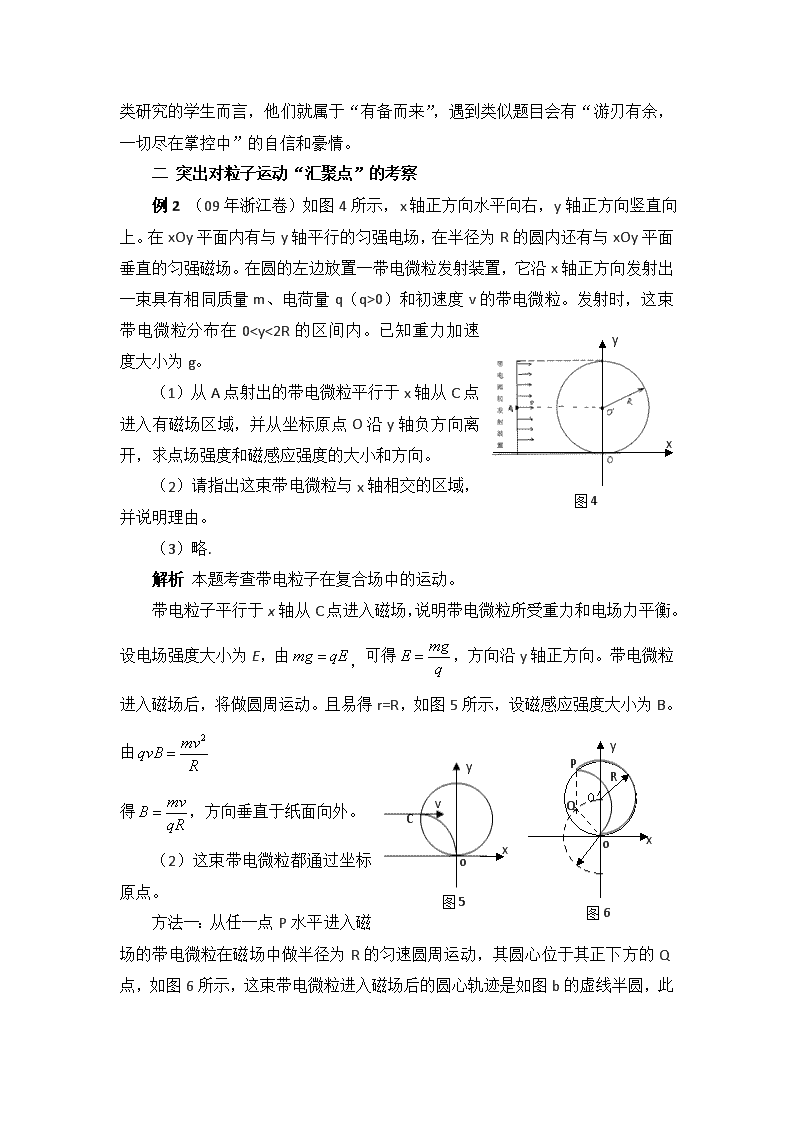
一类平面磁聚焦模型在高考和竞赛中的应用 周红卫 (宁波万里国际学校 315040) 带电粒子在磁场(或复合场)中的运动是高考的常考题型,在各省市的高考中都处于主角的位置。在诸多的带电粒子在磁场中的运动问题中,有一类平行运动的等速粒子的平面磁聚焦问题很受青睐,在竞赛中也得到了体现。现对此进行一个举例分析。 Y X 0 V 图1 A5 A4 A3 A2 A1 模型的建立:如图1几何图形,若干个等半径的圆可以交于一点,这些圆的圆心自身也落在一个同样大小的圆上。假设我们以此交点为原点建立一个坐标系,做每个圆最顶端的切线,这些切线互相平行,这些切点刚好落在同样大小的另一个圆上。我们可以依此图形为基础,构造一个物理上的带电粒子运动模型:假设一束互相平行的带电粒子平行于x轴射来,刚好从各圆的切点处进入一个匀强磁场,由于其圆周运动的半径相同,各粒子将按照切点以右的圆周运动,最后将汇聚于原点O。反之,假设从原点处向x轴以上各个方向发射速度相等的同中粒子,且刚好运动到水平方向时失去磁场,那么这些粒子将平行于x轴向x轴负向运动。在此基础上构造的物理模型在高考和竞赛中频频出现,以下几例为证。 一 突出对粒子运动径迹的考察 例1 (09年海南卷)如图2,ABCD是边长为的正方形。质量为、电荷量为的电子以大小为的初速度沿纸面垂直于BC变射入正方形区域。在正方形内适当区域中有匀强磁场。电子从BC边上的任意点入射,都只能从A点射出磁场。不计重力,求: 图3 (1)次匀强磁场区域中磁感应强度的方向和大小; (2)此匀强磁场区域的最小面积。 A BA CBA DCBA 图2 解析 (1)设匀强磁场的磁感应强度的大小为B。令圆弧是自C点垂直于BC入射的电子在磁场中的运行轨道。电子所受到的磁场的作用力大小为,方向应指向圆弧的圆心,因而磁场的方向应垂直于纸面向外。圆弧AEC的圆心在CB边或其延长线上。依题意,圆心在A、C连线的中垂线上,故B点即为圆心,圆半径为,按照牛顿定律有 联立两式得 (2)由(1)中决定的磁感应强度的方向和大小,可知自点垂直于入射电子在A点沿DA方向射出,且自BC边上其它点垂直于入射的电子的运动轨道只能在BAEC区域中。因而,圆弧AEC是所求的最小磁场区域的一个边界。 为了决定该磁场区域的另一边界,我们来考察射中A点的电子的速度方向与BA的延长线交角为(不妨设)的情形。该电子的运动轨迹如图3所示。图中,圆弧AP的圆心为O,pq垂直于BC边 ,由知,圆弧AP的半径仍为,在以A为原点、AB为x轴,AD为轴的坐标系中,P点的坐标为 消去参数θ得 这意味着,在范围内,p点形成以D为圆心、为半径的四分之一圆周,它是电子做直线运动和圆周运动的分界线,构成所求磁场区域的另一边界。因此,所求的最小匀强磁场区域时分别以和为圆心、为半径的两个四分之一圆周和所围成的,其面积为 点评 这是一个典型的利用磁场进行平行运动带电粒子磁聚焦的考题,看起来在考磁场的最小面积问题,但实质上在考核粒子的运动径迹。 从知识和能力的角度看,对于面对陌生题目的考生而言,综合考查了学生对于带电粒子在磁场中运动的综合分析能力,这类题目也是几乎所有高考题目的选择对象。但对于平时对平行运动带电粒子磁聚焦问题有过深入分析和研究,对带电粒子的运动做过分类研究的学生而言,他们就属于“有备而来”,遇到类似题目会有“游刃有余,一切尽在掌控中”的自信和豪情。 二 突出对粒子运动“汇聚点”的考察 例2 (09年浙江卷)如图4所示,x轴正方向水平向右,y轴正方向竖直向上。在xOy平面内有与y轴平行的匀强电场,在半径为R的圆内还有与xOy平面垂直的匀强磁场。在圆的左边放置一带电微粒发射装置,它沿x轴正方向发射出一束具有相同质量m、电荷量q(q>0)和初速度v的带电微粒。发射时,这束带电微粒分布在0查看更多
相关文章
- 当前文档收益归属上传用户