- 2021-05-13 发布 |
- 37.5 KB |
- 5页

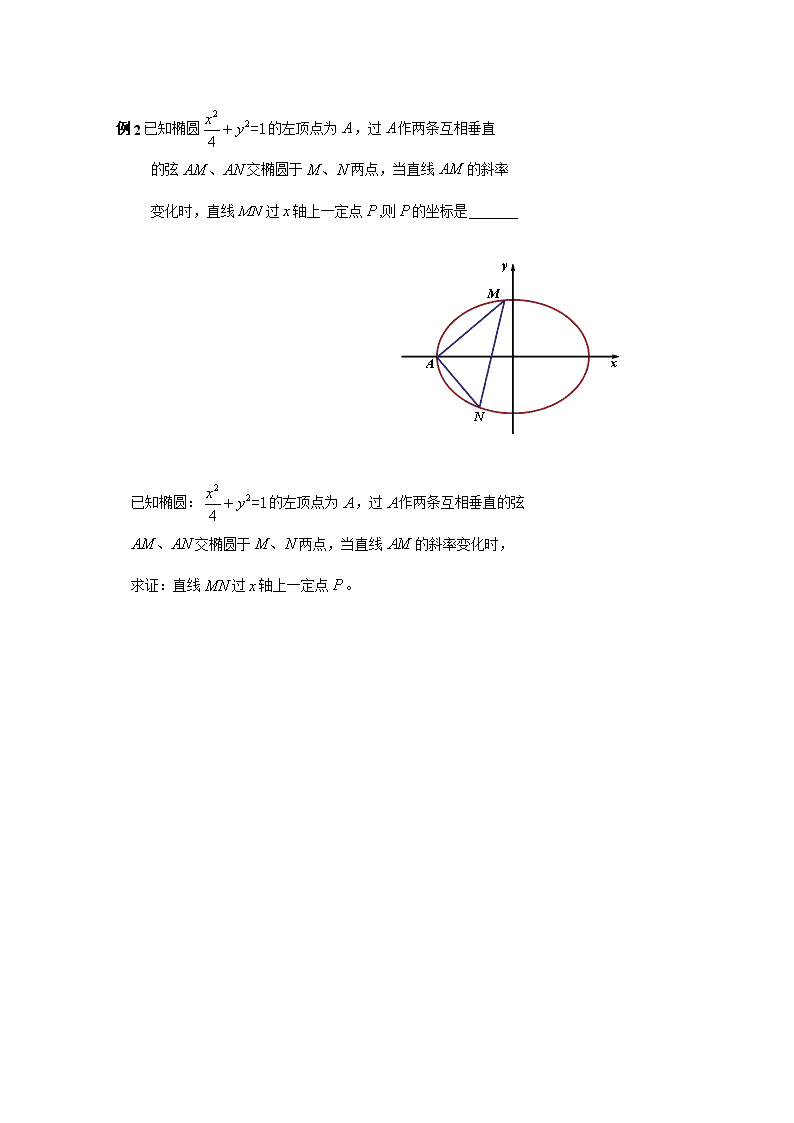

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考数学复习学案椭圆的综合应用
教学目标:理解和深刻认识椭圆的定义和椭圆的性质;会利用椭圆的定义和性质解椭圆的简单综合应用题。 教学重点、难点:利用椭圆的定义和性质求解椭圆的综合题 教学方法:讲练结合 教学过程: 一、【课堂练习】 例1在平面直角坐标系xoy中,椭圆C的中心为原点,焦点F1,F2在x轴上,离心率为,过点F1的直线 l交椭圆C于A,B两点,且的周长为16,则椭圆C的方程为 【变】在平面直角坐标系xoy圆C的中心为原点,焦点在坐标轴上, 离心率为.抛物线的焦点为F,点P是抛物线与椭圆C的公共点,且PF=3,那么椭圆C的方程为___ ______. 例2已知椭圆的左顶点为,过作两条互相垂直 的弦交椭圆于两点,当直线的斜率 变化时,直线过轴上一定点,则的坐标是 已知椭圆:的左顶点为,过作两条互相垂直的弦 交椭圆于两点,当直线的斜率变化时, 求证:直线过轴上一定点。 例3已知点和点分别是椭圆的中心和左焦点,点是椭圆上任意一点,则的最大值是 【练习】已知椭圆C:(常数),点是椭圆C上的一动点,点 是椭圆的右顶点,定点(2,0)。 (1) 若,求线段的最值。 (2) 若线段的最小值为线段,求的取值范围。 1、已知椭圆+=1与双曲线-=1(m,n,p,q∈R+)有共同的焦点F1、F2,P是椭圆和双曲线的一个交点,则|PF1|·|PF2|= . 答案: 提示:令F1为左焦点,F2为右焦点,P为第一象限内点, 则,∴. 点评:涉及到椭圆、双曲线的焦点弦、焦半径——常常用到相关定义或第二定义. 2、已知椭圆G:+=1(a>b>0),直线l为圆O:x2+y2=b2的一条切线,且经过椭圆的右焦点,记椭圆离心率为e. (1)若直线l的倾斜角为,求e的值; (2)是否存在这样的椭圆G,使得原点O关于直线l的对称点恰好在椭圆G上? 请求出e的值;若不存在,请说明理由. 思路透析:(1)设椭圆的右焦点为(c,0),x=. 则直线l的方程为y=(x-c)×tan,即x-y-c=0. 因为直线l与圆O相切,所以圆心O到直线l的距离=b,即b=c. 所以a2=b2+c 2=c 2,从而离心率e==. (2)假设存在.显然直线l的斜率不为0,不妨设直线l的方程为x=my+c, 即x-my-c=0.因为直线l与圆O相切,所以圆心O到直线l的距离=b,即m2=-1.…①设原点O关于直线l的对称点为O¢(x0,y0),则,解得.因为O′在椭圆G上,所以+=1,即+=1.…② 将①代入②,化简,得b2=3c 2. 由①可得,此时m2=-1=-,不成立. 点评:椭圆是否存在——“几何” 问题,转化为方程(组)是否有解——“代数”问题,这正是解析几何中所体现的最基本的思想方法. 查看更多