- 2021-05-13 发布 |
- 37.5 KB |
- 26页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
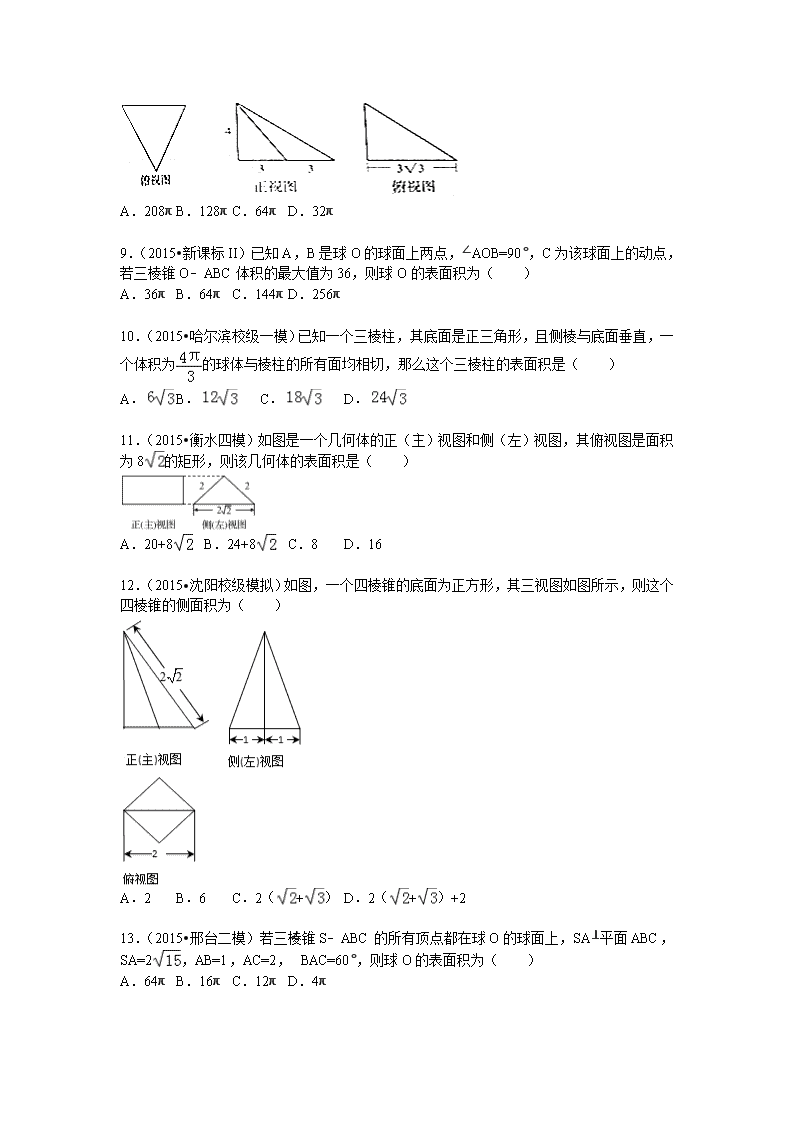
高考试题—锥体与球体的表面积或体积
2016年03月13日沐玖的高中数学组卷 一.选择题(共30小题) 1.(2015•徐汇区模拟)长方体的一个顶点上三条棱长为3、4、5,且它的八个顶点都在一个球面上,这个球的表面积是( ) A.20π B.25π C.50π D.200π 2.(2014•广西模拟)将边长为a的正方形ABCD沿对角线AC折起,使得BD=a,则三棱锥D﹣ABC的体积为( ) A. B. C. D. 3.(2014春•滦南县期末)长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在同一球面上,则这个球的表面积是( ) A.25π B.50π C.125π D.都不对 4.(2000•天津)一个圆柱的侧面展开图是一个正方形,这个圆柱的全面积与侧面积的比是( ) A. B. C. D. 5.(2015•武汉校级模拟)某几何体的三视图如图所示,当xy最大时,该几何体的体积为( ) A.2 B.4 C.8 D.16 6.(2015•沈阳模拟)若某简单空间几何体的三视图都是边长为1的正方形,则这个空间几何体的内切球的体积为( ) A.π B.π C. D.π 7.(2016•宝鸡一模)已知三角形PAD所在平面与矩形ABCD所在平面互相垂直,PA=PD=AB=2,∠APD=90°,若点P、A、B、C、D都在同一球面上,则此球的表面积等于( ) A.4π B.π C.12π D.20π 8.(2016•宿州一模)某几何体的三视图如图所示,则该几何体的外接球的表面积是( ) A.208π B.128π C.64π D.32π 9.(2015•新课标II)已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O﹣ABC体积的最大值为36,则球O的表面积为( ) A.36π B.64π C.144π D.256π 10.(2015•哈尔滨校级一模)已知一个三棱柱,其底面是正三角形,且侧棱与底面垂直,一个体积为的球体与棱柱的所有面均相切,那么这个三棱柱的表面积是( ) A. B. C. D. 11.(2015•衡水四模)如图是一个几何体的正(主)视图和侧(左)视图,其俯视图是面积为8的矩形,则该几何体的表面积是( ) A.20+8 B.24+8 C.8 D.16 12.(2015•沈阳校级模拟)如图,一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的侧面积为( ) A.2 B.6 C.2(+) D.2(+)+2 13.(2015•邢台二模)若三棱锥S﹣ABC的所有顶点都在球O的球面上,SA⊥平面ABC,SA=2,AB=1,AC=2,∠BAC=60°,则球O的表面积为( ) A.64π B.16π C.12π D.4π 14.(2015•厦门模拟)如图1,已知正方体ABCD﹣A1B1C1D1的棱长为a,动点M,N,Q分别在线段AD1,B1C,C1D1上,当三棱锥Q﹣BMN的俯视图如图2所示,三棱锥Q﹣BMN正视图的面积等于( ) A. B.a2 C. D.a2 15.(2015•河池一模)一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图所示,则该几何体的体积为( ) A.9 B.10 C.11 D. 16.(2015秋•深圳校级期末)设三棱柱ABC﹣A1B1C1的体积为V,P、Q分别是侧棱AA1、CC1上的点,且PA=QC1,则四棱锥B﹣APQC的体积为( ) A. B. C. D. 17.(2015•沈阳一模)已知某几何体的三视图如,根据图中标出的尺寸 (单位:cm),可得这个几何体的体积是( ) A. B. C.2cm3 D.4cm3 18.(2015•武昌区模拟)如图,取一个底面半径和高都为R的圆柱,从圆柱中挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥,把所得的几何体与一个半径为R的半球放在同一水平面α上.用一平行于平面α的平面去截这两个几何体,截面分别为圆面和圆环面(图中阴影部分).设截面面积分别为S圆和S圆环,那么( ) A.S圆>S圆环 B.S圆=S圆环 C.S圆<S圆环 D.不确定 19.(2015•重庆模拟)已知四面体P﹣ABC的外接球的球心O在AB上,且PO⊥平面ABC,2AC=AB,若四面体P﹣ABC的体积为,则该球的体积为( ) A. B.2π C. D. 20.(2015•河池一模)将一张边长为6cm的纸片按如图1所示的阴影部分截去四个全等的等腰三角形,将剩余下部分沿虚线折叠并拼成一个有底的正四棱锥(底面是正方形,顶点在底面的射影为正方形的中心)模型,如图2放置,若正四棱锥的正视图是正三角形(如图3),则正四棱锥的体积是( ) A.cm3 B.cm3 C.cm3 D.cm3 21.(2015•天津校级模拟)正三棱柱体积为V,则其表面积最小时,底面边长为( ) A. B. C. D.2 22.(2015•石家庄一模)在棱长为3的正方体ABCD﹣A1B1C1D1中,P在线段BD1上,且,M为线段B1C1上的动点,则三棱锥M﹣PBC的体积为( ) A.1 B. C. D.与M点的位置有关 23.(2015•昌平区二模)已知四面体A﹣BCD满足下列条件: (1)有一个面是边长为1的等边三角形; (2)有两个面是等腰直角三角形. 那么四面体A﹣BCD的体积的取值集合是( ) A. B. C. D. 24.(2015•大连二模)已知三棱锥P﹣ABC的外接球的球心O在AB上,且PO⊥平面ABC,2AC=AB,若三棱锥P﹣ABC的体积为,则该三棱锥的外接球的体积为( ) A.8π B.6π C.4π D.2π 25.(2015•银川校级三模)以下是某个几何体的三视图(单位:cm),则该几何体的体积是( ) A.2cm3 B.3cm3 C.4cm3 D.5cm3 26.(2015•嘉定区二模)在四棱锥V﹣ABCD中,B1,D1分别为侧棱VB、VD的中点,则四面体AB1CD1的体积与四棱锥V﹣ABCD的体积之比为( ) A.1:6 B.1:5 C.1:4 D.1:3 27.(2015•赤峰模拟)在正棱柱ABC﹣A1B1C1中,A1C1=2,AA1=,D为BC的中点,则三棱锥A﹣B1DC1的体积为( ) A. B.2 C.1 D.3 28.(2015•宁城县一模)某四棱锥的三视图如图所示,其中正(主)视图是等腰直角三角形,侧(左)视图是等腰三角形,俯视图是正方形,则该四棱锥的体积是( ) A. B. C. D. 29.(2015•黄山二模)在空间直角坐标系O﹣xyz中,四面体ABCD的顶点坐标分别是(1,0,1),(1,1,0),(0,1,1)(0,0,0),则该四面体的正视图的面积不可能为( ) A. B. C. D. 30.(2015•兰州模拟)已知长方体ABCD﹣A1B1C1D1的各个顶点都在表面积为16π的球面上,且AB=AD,AA1=2AD,则四棱锥D1﹣ABCD的体积为( ) A. B. C.2 D.4 2016年03月13日沐玖的高中数学组卷 参考答案与试题解析 一.选择题(共30小题) 1.(2015•徐汇区模拟)长方体的一个顶点上三条棱长为3、4、5,且它的八个顶点都在一个球面上,这个球的表面积是( ) A.20π B.25π C.50π D.200π 【考点】球的体积和表面积.菁优网版权所有 【专题】计算题. 【分析】设出球的半径,由于直径即是长方体的体对角线,由此关系求出球的半径,即可求出球的表面积. 【解答】解:设球的半径为R,由题意,球的直径即为长方体的体对角线,则(2R)2=32+42+52=50, ∴R=. ∴S球=4π×R2=50π. 故选C 【点评】本题考查球的表面积,球的内接体,考查计算能力,是基础题. 2.(2014•广西模拟)将边长为a的正方形ABCD沿对角线AC折起,使得BD=a,则三棱锥D﹣ABC的体积为( ) A. B. C. D. 【考点】棱柱、棱锥、棱台的体积.菁优网版权所有 【专题】计算题. 【分析】取AC的中点O,连接DO,BO,求出三角形DOB的面积,求出AC的长,即可求三棱锥D﹣ABC的体积. 【解答】解:O是AC中点,连接DO,BO,如图, △ADC,△ABC都是等腰直角三角形, DO=B0==,BD=a, △BDO也是等腰直角三角形,DO⊥AC,DO⊥BO,DO⊥平面ABC, DO就是三棱锥D﹣ABC的高, S△ABC=a2三棱锥D﹣ABC的体积:, 故选D. 【点评】本题考查棱锥的体积,是基础题. 3.(2014春•滦南县期末)长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在同一球面上,则这个球的表面积是( ) A.25π B.50π C.125π D.都不对 【考点】球的体积和表面积;球内接多面体.菁优网版权所有 【专题】计算题. 【分析】由题意长方体的外接球的直径就是长方体的对角线,求出长方体的对角线,就是求出球的直径,然后求出球的表面积. 【解答】解:因为长方体的一个顶点上的三条棱长分别是3,4,5,且它的8个顶点都在同一个球面上, 所以长方体的对角线就是确定直径,长方体的对角线为:, 所以球的半径为:, 所以这个球的表面积是:=50π. 故选B. 【点评】本题是基础题,考查球的内接多面体的有关知识,球的表面积的求法,注意球的直径与长方体的对角线的转化是本题的解答的关键,考查计算能力,空间想象能力. 4.(2000•天津)一个圆柱的侧面展开图是一个正方形,这个圆柱的全面积与侧面积的比是( ) A. B. C. D. 【考点】棱柱、棱锥、棱台的侧面积和表面积;旋转体(圆柱、圆锥、圆台).菁优网版权所有 【专题】计算题. 【分析】设圆柱底面积半径为r,求出圆柱的高,然后求圆柱的全面积与侧面积的比. 【解答】解:设圆柱底面积半径为r,则高为2πr, 全面积:侧面积=[(2πr)2+2πr2]:(2πr)2 =. 故选A. 【点评】本题考查圆柱的侧面积、表面积,考查计算能力,是基础题. 5.(2015•武汉校级模拟)某几何体的三视图如图所示,当xy最大时,该几何体的体积为( ) A.2 B.4 C.8 D.16 【考点】棱柱、棱锥、棱台的体积.菁优网版权所有 【专题】空间位置关系与距离. 【分析】首先,根据三视图,得到该几何体的具体的结构特征,然后,建立关系式:,然后,求解当xy最大时,该几何体的具体的结构,从而求解其体积. 【解答】解:由三视图,得 该几何体为三棱锥, 有, ∴x2+y2=128, ∵xy≤,当且仅当x=y=8时,等号成立, 此时,V=××2×6×8=16, 故选:D. 【点评】本题重点考查了三视图、几何体的体积计算等知识,属于中档题. 6.(2015•沈阳模拟)若某简单空间几何体的三视图都是边长为1的正方形,则这个空间几何体的内切球的体积为( ) A.π B.π C. D.π 【考点】球的体积和表面积.菁优网版权所有 【专题】计算题;空间位置关系与距离. 【分析】根据几何体的三视图是边长为1的正方形,得几何体是棱长为1的正方体,即可求出这个空间几何体的内切球的体积. 【解答】解:根据几何体的三视图是边长为1的正方形,得几何体是棱长为1的正方体, ∴几何体的内切球的体积为V=π×()3=. 故选:D. 【点评】本题考查了由三视图求这个空间几何体的内切球的体积,判断几何体的形状是关键. 7.(2016•宝鸡一模)已知三角形PAD所在平面与矩形ABCD所在平面互相垂直,PA=PD=AB=2,∠APD=90°,若点P、A、B、C、D都在同一球面上,则此球的表面积等于( ) A.4π B.π C.12π D.20π 【考点】球的体积和表面积.菁优网版权所有 【专题】计算题;空间位置关系与距离. 【分析】设球心为O,由点P、A、B、C、D都在同一球面上,可得球的直径就是矩形对角线的长,求得球的半径,从而得出表面积. 【解答】解:设球心为O,如图. 由PA=PD=AB=2,∠APD=90°,可求得AD=2, 在矩形ABCD中,可求得对角线BD==2, 由于点P、A、B、C、D都在同一球面上, ∴球的半径R=BD= 则此球的表面积等于=4πR2=12π. 故选:C. 【点评】本题是中档题,考查球的体积和表面积,解题的根据是点P、A、B、C、D都在同一球面上,考查计算能力,空间想象能力. 8.(2016•宿州一模)某几何体的三视图如图所示,则该几何体的外接球的表面积是( ) A.208π B.128π C.64π D.32π 【考点】球的体积和表面积;球内接多面体.菁优网版权所有 【专题】计算题;数形结合;综合法;立体几何. 【分析】几何体为三棱锥,且三棱锥的一条侧棱垂直于底面,结合直观图判断外接球半径,代入求得表面积公式计算. 【解答】解:由三视图知:几何体为三棱锥,且三棱锥的一条侧棱垂直于底面,高为4, 底面为等腰三角形,底边长为6,高为3. ∴△ABC为等边三角形,外接圆的半径r=2, ∴几何体的外接球的半径R==4, ∴外接球的表面积S=4π×16=64π. 故选:C. 【点评】本题考查了由三视图求几何体的外接球的表面积,根据三视图判断几何体的结构特征,利用几何体的结构特征与数据求得外接球的半径是解答本题的关键. 9.(2015•新课标II)已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O﹣ABC体积的最大值为36,则球O的表面积为( ) A.36π B.64π C.144π D.256π 【考点】球的体积和表面积.菁优网版权所有 【专题】计算题;空间位置关系与距离. 【分析】当点C位于垂直于面AOB的直径端点时,三棱锥O﹣ABC的体积最大,利用三棱锥O﹣ABC体积的最大值为36,求出半径,即可求出球O的表面积. 【解答】解:如图所示,当点C位于垂直于面AOB的直径端点时,三棱锥O﹣ABC的体积最大,设球O的半径为R,此时VO﹣ABC=VC﹣AOB===36,故R=6,则球O的表面积为4πR2=144π, 故选C. 【点评】本题考查球的半径与表面积,考查体积的计算,确定点C位于垂直于面AOB的直径端点时,三棱锥O﹣ABC的体积最大是关键. 10.(2015•哈尔滨校级一模)已知一个三棱柱,其底面是正三角形,且侧棱与底面垂直,一个体积为的球体与棱柱的所有面均相切,那么这个三棱柱的表面积是( ) A. B. C. D. 【考点】棱柱、棱锥、棱台的侧面积和表面积.菁优网版权所有 【专题】计算题;空间位置关系与距离. 【分析】由球的体积可以求出半径,从而得棱柱的高;由球与正三棱柱的三个侧面相切,得球的半径和棱柱底面正△边长的关系,求出边长,即求出底面正△的面积;得出棱柱的表面积. 【解答】解:由球的体积公式,得πR3=, ∴R=1. ∴正三棱柱的高h=2R=2. 设正三棱柱的底面边长为a,则其内切圆的半径为:•a=1, ∴a=2. ∴该正三棱柱的表面积为:3a•2R+2×=18. 故选C. 【点评】本题考查了球的体积,柱体体积公式的应用;本题的解题关键是求底面边长,这是通过正△的内切圆与边长的关系得出的. 11.(2015•衡水四模)如图是一个几何体的正(主)视图和侧(左)视图,其俯视图是面积为8的矩形,则该几何体的表面积是( ) A.20+8 B.24+8 C.8 D.16 【考点】棱柱、棱锥、棱台的侧面积和表面积.菁优网版权所有 【专题】计算题;空间位置关系与距离. 【分析】由三视图及题设条件知,此几何体为一个三棱柱,底面是等腰直角三角形,且其高为,故先求出底面积,求解其表面积即可. 【解答】解:此几何体是一个三棱柱,且其高为=4, 由于其底面是一个等腰直角三角形,直角边长为2,所以其面积为×2×2=2, 又此三棱柱的高为4,故其侧面积为(2+2+2)×4=16+8, 表面积为:2×2+16+8=20+8. 故选A. 【点评】本题考点是由三视图求几何体的面积、体积,考查对三视图的理解与应用,主要考查三视图与实物图之间的关系,用三视图中的数据还原出实物图的数据,再根据相关的公式求表面积三视图的投影规则是:“主视、俯视 长对正;主视、左视高平齐,左视、俯视 宽相等”. 12.(2015•沈阳校级模拟)如图,一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的侧面积为( ) A.2 B.6 C.2(+) D.2(+)+2 【考点】棱柱、棱锥、棱台的侧面积和表面积.菁优网版权所有 【专题】空间位置关系与距离. 【分析】根据三视图得出空间几何体的直观图,运用几何体的性质求解侧面积. 【解答】解: 根据三视图画出直观图, 得出:PA=2,AC=2,AB=,PB=, PA⊥面ABCD,四边形ABCD为正方形, ∴这个四棱锥的侧面积为2××+2×××=2(), 故选:C 【点评】本题考查了空间几何体的三视图,空间几何体的性质,关键是确定直观图,恢复得出直线平面的位置关系,属于中档题. 13.(2015•邢台二模)若三棱锥S﹣ABC的所有顶点都在球O的球面上,SA⊥平面ABC,SA=2,AB=1,AC=2,∠BAC=60°,则球O的表面积为( ) A.64π B.16π C.12π D.4π 【考点】棱柱、棱锥、棱台的侧面积和表面积;棱柱、棱锥、棱台的体积.菁优网版权所有 【专题】计算题;空间位置关系与距离. 【分析】由三棱锥S﹣ABC的所有顶点都在球O的球面上,AB=1,AC=2,∠BAC=60°,知BC,∠ABC=90°,可得△ABC截球O所得的圆O′的半径,利用SA⊥平面ABC,SA=2,此能求出球O的半径,从而能求出球O的表面积. 【解答】解:如图,三棱锥S﹣ABC的所有顶点都在球O的球面上, ∵AB=1,AC=2,∠BAC=60°, ∴BC=, ∴∠ABC=90°. ∴△ABC截球O所得的圆O′的半径r=1, ∵SA⊥平面ABC,SA=2 ∴球O的半径R=4, ∴球O的表面积S=4πR2=64π. 故选:A. 【点评】本题考查球的表面积的求法,合理地作出图形,数形结合求出球半径,是解题的关键. 14.(2015•厦门模拟)如图1,已知正方体ABCD﹣A1B1C1D1的棱长为a,动点M,N,Q分别在线段AD1,B1C,C1D1上,当三棱锥Q﹣BMN的俯视图如图2所示,三棱锥Q﹣BMN正视图的面积等于( ) A. B.a2 C. D.a2 【考点】棱柱、棱锥、棱台的侧面积和表面积.菁优网版权所有 【专题】计算题;空间位置关系与距离. 【分析】由三棱锥Q﹣BMN的俯视图可得Q在D1,N在C,所以三棱锥Q﹣BMN正视图为△D1EC(E为D1D的中点),即可求出三棱锥Q﹣BMN正视图的面积. 【解答】解:由三棱锥Q﹣BMN的俯视图可得Q在D1,N在C, 所以三棱锥Q﹣BMN正视图为△D1EC(E为D1D的中点), 其面积为=. 故选:B. 【点评】本题考查三棱锥Q﹣BMN正视图的面积,考查学生的计算能力,确定三棱锥Q﹣BMN正视图为△D1EC是关键. 15.(2015•河池一模)一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图所示,则该几何体的体积为( ) A.9 B.10 C.11 D. 【考点】棱柱、棱锥、棱台的体积.菁优网版权所有 【专题】空间位置关系与距离. 【分析】根据得出该几何体是在底面为边长是2的正方形、高是3的直四棱柱的基础上, 截去一个底面积为×2×1=1、高为3的三棱锥形成的,运用直棱柱减去三棱锥即可得出答案. 【解答】解:.由三视图可知该几何体是在底面为边长是2的正方形、高是3的直四棱柱的基础上, 截去一个底面积为×2×1=1、高为3的三棱锥形成的,V三棱锥==1, 所以V=4×3﹣1=11. 故选:C 【点评】本题考查了空间几何体的性质,求解体积,属于计算题,关键是求解底面积,高,运用体积公式. 16.(2015秋•深圳校级期末)设三棱柱ABC﹣A1B1C1的体积为V,P、Q分别是侧棱AA1、CC1上的点,且PA=QC1,则四棱锥B﹣APQC的体积为( ) A. B. C. D. 【考点】棱柱、棱锥、棱台的体积.菁优网版权所有 【专题】计算题. 【分析】由已知中三棱柱ABC﹣A1B1C1的体积为V,P、Q分别是侧棱AA1、CC1上的点,且PA=QC1,我们可得SAPQC=,即VB﹣APQC=,再结合同底等高的棱柱的体积为棱锥体积的3倍,即可求出答案. 【解答】解:∵三棱柱ABC﹣A1B1C1的体积为V, 又∵P、Q分别是侧棱AA1、CC1上的点,且PA=QC1, ∴四棱锥B﹣APQC的底面积SAPQC= 又VB﹣ACC1A1= ∴VB﹣APQC=== 故选C. 【点评】本题考查的知识点是棱柱的体积、棱锥的体积,其中分析出棱锥与原棱柱之间底面积、高之间的比例关系是解答本题的关键. 17.(2015•沈阳一模)已知某几何体的三视图如,根据图中标出的尺寸 (单位:cm),可得这个几何体的体积是( ) A. B. C.2cm3 D.4cm3 【考点】棱柱、棱锥、棱台的体积.菁优网版权所有 【专题】空间位置关系与距离. 【分析】由题目给出的几何体的三视图,还原得到原几何体,然后直接利用三棱锥的体积公式求解. 【解答】解:由三视图可知,该几何体为底面是正方形,且边长为2cm,高为2cm的四棱锥, 如图, 故, 故选B. 【点评】本题考查了棱锥的体积,考查了空间几何体的三视图,能够由三视图还原得到原几何体是解答该题的关键,是基础题. 18.(2015•武昌区模拟)如图,取一个底面半径和高都为R的圆柱,从圆柱中挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥,把所得的几何体与一个半径为R的半球放在同一水平面α上.用一平行于平面α的平面去截这两个几何体,截面分别为圆面和圆环面(图中阴影部分).设截面面积分别为S圆和S圆环,那么( ) A.S圆>S圆环 B.S圆=S圆环 C.S圆<S圆环 D.不确定 【考点】棱柱、棱锥、棱台的体积.菁优网版权所有 【专题】空间位置关系与距离. 【分析】根据图形得出,S截面圆=π(R2﹣d2),r=d,S圆环=π(R2﹣d2),即可判断. 【解答】解:根据题意:∵①半球的截面圆:r=,S截面圆=π(R2﹣d2), ②∵取一个底面半径和高都为R的圆柱,从圆柱中挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥, ∴r=d,S圆环=π(R2﹣d2), 根据①②得出:S截面圆=S圆环, 故选:B 【点评】本题考查了球有关的截面问题,判断图形结构,求出半径即可,属于中档题. 19.(2015•重庆模拟)已知四面体P﹣ABC的外接球的球心O在AB上,且PO⊥平面ABC,2AC=AB,若四面体P﹣ABC的体积为,则该球的体积为( ) A. B.2π C. D. 【考点】棱柱、棱锥、棱台的体积.菁优网版权所有 【专题】计算题;空间位置关系与距离. 【分析】设该球的半径为R,则AB=2R,2AC=AB=,故AC=R,由于AB是球的直径,所以△ABC在大圆所在平面内且有AC⊥BC,由此能求出球的体积. 【解答】解:设该球的半径为R, 则AB=2R,2AC=AB=, ∴AC=R, 由于AB是球的直径, 所以△ABC在大圆所在平面内且有AC⊥BC, 在Rt△ABC中,由勾股定理,得: BC2=AB2﹣AC2=R2, 所以Rt△ABC面积S=×BC×AC=, 又PO⊥平面ABC,且PO=R,四面体P﹣ABC的体积为, ∴VP﹣ABC==, 即R3=9,R3=3, 所以:球的体积V球=×πR3=×π×3=4π. 故选D. 【点评】本题考查四面体的外接球的体积的求法,解题时要认真审题,仔细解答,注意合理地化空间问题为平面问题. 20.(2015•河池一模)将一张边长为6cm的纸片按如图1所示的阴影部分截去四个全等的等腰三角形,将剩余下部分沿虚线折叠并拼成一个有底的正四棱锥(底面是正方形,顶点在底面的射影为正方形的中心)模型,如图2放置,若正四棱锥的正视图是正三角形(如图3),则正四棱锥的体积是( ) A.cm3 B.cm3 C.cm3 D.cm3 【考点】棱柱、棱锥、棱台的体积.菁优网版权所有 【专题】空间位置关系与距离. 【分析】根据图形正四棱锥的正视图是正三角形,正视图的底面边长为a,高为a,正四棱锥的斜高为a,运用图1得出;×6=,a=2,计算计算出a,代入公式即可. 【解答】解: ∵正四棱锥的正视图是正三角形,正视图的底面边长为a,高为a, ∴正四棱锥的斜高为a, ∵图1得出:∵将一张边长为6cm的纸片按如图1所示的阴影部分截去四个全等的等腰三角形 ∴×6=,a=2, ∴正四棱锥的体积是a2×a=, 故选:A 【点评】本题综合考查了空间几何体的性质,展开图与立体图的结合,需要很好的空间思维能力,属于中档题. 21.(2015•天津校级模拟)正三棱柱体积为V,则其表面积最小时,底面边长为( ) A. B. C. D.2 【考点】棱柱、棱锥、棱台的体积.菁优网版权所有 【专题】计算题;空间位置关系与距离. 【分析】设底边边长为a,高为h,利用体积公式V=Sh得出h,再根据表面积公式得S=3ah+2•=+,最后利用导函数即得底面边长. 【解答】解:设底边边长为a,高为h, 则V=Sh=a2×h, ∴h=, 则表面积为S=3ah+2•=+, 则令S′=a﹣=0, 解得a=即为所求边长. 故选:B. 【点评】本小题主要考查棱柱、棱锥、棱台、棱柱、棱锥、棱台的侧面积和表面积、基本不等式等基础知识,考查运算求解能力,考查转化思想.属于基础题. 22.(2015•石家庄一模)在棱长为3的正方体ABCD﹣A1B1C1D1中,P在线段BD1上,且,M为线段B1C1上的动点,则三棱锥M﹣PBC的体积为( ) A.1 B. C. D.与M点的位置有关 【考点】棱柱、棱锥、棱台的体积.菁优网版权所有 【专题】空间位置关系与距离. 【分析】如图所示,连接BC1,取=,可得PN∥D1C1,=1,由于D1C1⊥平面BCC1B1,可得PN⊥平面BCC1B1,利用三棱锥M﹣PBC的体积=V三棱锥P﹣BCM=即可得出. 【解答】解:如图所示,连接BC1,取=, 则PN∥D1C1,,PN=1, ∵D1C1⊥平面BCC1B1, ∴PN⊥平面BCC1B1, 即PN是三棱锥P﹣BCM的高. ∴V三棱锥M﹣PBC=V三棱锥P﹣BCM===. 故选:B. 【点评】本题考查了正方体的性质、线面垂直的判定与性质定理、三角形中平行线分线段成比例定理的逆定理、三棱锥的体积计算公式,考查了推理能力与计算能力,属于中档题. 23.(2015•昌平区二模)已知四面体A﹣BCD满足下列条件: (1)有一个面是边长为1的等边三角形; (2)有两个面是等腰直角三角形. 那么四面体A﹣BCD的体积的取值集合是( ) A. B. C. D. 【考点】棱柱、棱锥、棱台的体积.菁优网版权所有 【专题】综合题;空间位置关系与距离. 【分析】由题意,分类讨论,(1)△BCD是等边三角形,BA⊥AC,DA⊥AC;(2)△BCD是等边三角形,BA⊥BD,BA⊥BC;△BCD是等边三角形,BA⊥BD,DC⊥AC,求出体积即可. 【解答】解:由题意,分类讨论可得 (1)△BCD是等边三角形,BA⊥AC,DA⊥AC,所以四面体A﹣BCD的体积为=; (2)△BCD是等边三角形,BA⊥BD,BA⊥BC,所以四面体A﹣BCD的体积为=; (3)△BCD是等边三角形,BA⊥BD,DC⊥AC,取AD的中点O,可得BO=DO=,所以四面体A﹣BCD的体积为=. 故选:C. 【点评】本题考查三棱锥体积的计算,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题. 24.(2015•大连二模)已知三棱锥P﹣ABC的外接球的球心O在AB上,且PO⊥平面ABC,2AC=AB,若三棱锥P﹣ABC的体积为,则该三棱锥的外接球的体积为( ) A.8π B.6π C.4π D.2π 【考点】棱柱、棱锥、棱台的体积;球内接多面体.菁优网版权所有 【专题】空间位置关系与距离. 【分析】如图所示,由于三棱锥P﹣ABC的外接球的球心O在AB上,且PO⊥平面ABC,可得PO是三棱锥P﹣ABC的高,OA=OB=OC=OP=x,AC⊥BC.而2AC=AB,可得BC=x,AC=x.利用三棱锥的体积计算公式可得x,再利用球的体积计算公式即可得出. 【解答】解:如图所示, ∵三棱锥P﹣ABC的外接球的球心O在AB上,且PO⊥平面ABC, ∴PO是三棱锥P﹣ABC的高,OA=OB=OC=OP=x, ∴∠ACB=90°, ∴AC⊥BC. ∵2AC=AB, ∴∠ABC=60°, ∴BC=x,AC=x. ∴VP﹣ABC===, 解得x=. ∴该三棱锥的外接球的体积V==. 故选:C. 【点评】本题考查了线面垂直的性质、三棱锥的体积计算公式、球的体积计算公式,考查了推理能力与计算能力,属于中档题. 25.(2015•银川校级三模)以下是某个几何体的三视图(单位:cm),则该几何体的体积是( ) A.2cm3 B.3cm3 C.4cm3 D.5cm3 【考点】棱柱、棱锥、棱台的体积.菁优网版权所有 【专题】空间位置关系与距离. 【分析】由三视图得到原几何体,然后直接由棱柱的体积公式求得答案. 【解答】解:由三视图作出几何体原图形如图, 则原几何体为底面三角形是等腰三角形,高为3的直三棱柱, 且底面三角形ABC的面积为S=. ∴该几何体的体积V=S△ABC•EF=1×3=3(cm3). 故选:B. 【点评】本题考查几何体的三视图,关键是能由三视图得到原几何体,是中档题. 26.(2015•嘉定区二模)在四棱锥V﹣ABCD中,B1,D1分别为侧棱VB、VD的中点,则四面体AB1CD1的体积与四棱锥V﹣ABCD的体积之比为( ) A.1:6 B.1:5 C.1:4 D.1:3 【考点】棱柱、棱锥、棱台的体积.菁优网版权所有 【专题】空间位置关系与距离. 【分析】棱锥A﹣B1CD1的体积可以看成四棱锥P﹣ABCD的体积减去角上的四个小棱锥的体积得到,由B1,D1分别为侧棱VB、VD的中点,得到棱锥B1﹣ABC的体积与棱锥D1﹣ACD的体积和为四棱锥V﹣ABCD的体积的;棱锥B1﹣VAD1的体积与棱锥B1﹣VCD1的体积和为四棱锥V﹣ABCD的体积的.由此可得答案. 【解答】解:如图, 棱锥A﹣B1CD1的体积可以看成是四棱锥V﹣ABCD的体积减去角上的四个小棱锥的体积得到, ∵B1为PB的中点,D1为PD的中点, ∴棱锥B1﹣ABC的体积是棱锥V﹣ABC体积的,棱锥D1﹣ACD的体积是棱锥V﹣ACD的体积的, ∴棱锥B1﹣ABC的体积与棱锥D1﹣ACD的体积和为四棱锥V﹣ABCD的体积的; 棱锥B1﹣VAD1的体积是棱锥B﹣VAD体积的,棱锥B1﹣VCD1的体积是棱锥B﹣VCD体积的, ∴棱锥B1﹣VAD1的体积与棱锥B1﹣VCD1的体积和为四棱锥V﹣ABCD的体积的. 则中间剩下的棱锥A﹣B1CD1的体积V=四棱锥P﹣ABCD的体积﹣个四棱锥P﹣ABCD的体积 =个四棱锥P﹣ABCD的体积, 则两个棱锥A﹣B1CD1,P﹣ABCD的体积之比是1:4. 故选:C. 【点评】本题考查棱柱、棱锥、棱台的体积,利用分割法进行分割,是解题的关键,是中档题. 27.(2015•赤峰模拟)在正棱柱ABC﹣A1B1C1中,A1C1=2,AA1=,D为BC的中点,则三棱锥A﹣B1DC1的体积为( ) A. B.2 C.1 D.3 【考点】棱柱、棱锥、棱台的体积.菁优网版权所有 【专题】计算题;空间位置关系与距离. 【分析】由题意求出底面B1DC1的面积,求出A到底面的距离,即可求解三棱锥的体积. 【解答】解:∵正三棱柱ABC﹣A1B1C1的底面边长为2,侧棱长为,D为BC中点, ∴底面B1DC1的面积:=, A到底面的距离就是底面正三角形的高:. 三棱锥A﹣B1DC1的体积为:=1. 故选:C. 【点评】本题考查几何体的体积的求法,求解几何体的底面面积与高是解题的关键. 28.(2015•宁城县一模)某四棱锥的三视图如图所示,其中正(主)视图是等腰直角三角形,侧(左)视图是等腰三角形,俯视图是正方形,则该四棱锥的体积是( ) A. B. C. D. 【考点】棱柱、棱锥、棱台的体积.菁优网版权所有 【专题】空间位置关系与距离. 【分析】由三视图还原原直观图,可得三棱锥的底面是正方形,侧棱PA垂直于底面,且PA=2,求出底面积后直接代入棱锥的体积公式得答案. 【解答】解:由三视图还原原几何体如图, 底面ABCD为正方形,PA⊥底面ABCD,且PA=2, 底面ABCD的对角线线长为2, 则正方形ABCD的边长为, ∴, ∴=. 故选:B. 【点评】本题考查了三视图,考查了棱锥的体积,关键是由三视图还原原直观图,是中档题. 29.(2015•黄山二模)在空间直角坐标系O﹣xyz中,四面体ABCD的顶点坐标分别是(1,0,1),(1,1,0),(0,1,1)(0,0,0),则该四面体的正视图的面积不可能为( ) A. B. C. D. 【考点】棱柱、棱锥、棱台的体积;空间中的点的坐标.菁优网版权所有 【专题】空间位置关系与距离. 【分析】由题意画出几何体的直观图,可知直观图为连接棱长是1的正方体的四个顶点组成的正四面体,其最大正投影面为边长是1的正方形,由此断定其正视图的面积不会超过1,则答案可求. 【解答】解:一个四面体的顶点在空间直角坐标系O﹣xyz中的坐标分别是: (1,0,1),(1,1,0),(0,1,1),(0,0,0), 几何体的直观图如图,是以正方体的顶点为顶点的一个正四面体, 其正视图的最大投影面是在x﹣O﹣y或x﹣O﹣z或y﹣O﹣z面上, 投影面是边长为1的正方形,∴正视图的最大面积为1, ∴不可能为, 故选:D. 【点评】本小题主要考查空间线面关系、几何体的三视图等知识,考查数形结合的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力,是中档题. 30.(2015•兰州模拟)已知长方体ABCD﹣A1B1C1D1的各个顶点都在表面积为16π的球面上,且AB=AD,AA1=2AD,则四棱锥D1﹣ABCD的体积为( ) A. B. C.2 D.4 【考点】棱柱、棱锥、棱台的体积.菁优网版权所有 【专题】空间位置关系与距离. 【分析】设AD=x,长方体的外接球的半为R,利用=(2R2),4πR2=16π,解出x,R,再利用四棱锥的体积计算公式即可得出. 【解答】解:设AD=x,长方体的外接球的半为R, 则=(2R2),4πR2=16π, ∴+(2x)2=4R2,R2=4. 化为8x2=16, 解得x=, ∴四棱锥D1﹣ABCD的体积V===. 故选:B. 【点评】本题考查了线面垂直的判定与性质定理、长方体的对角线与外接球的直径直径的关系、四棱锥的体积计算公式,考查了推理能力与计算能力,属于中档题. 查看更多