- 2021-05-13 发布 |
- 37.5 KB |
- 10页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考真题分类汇编不等式
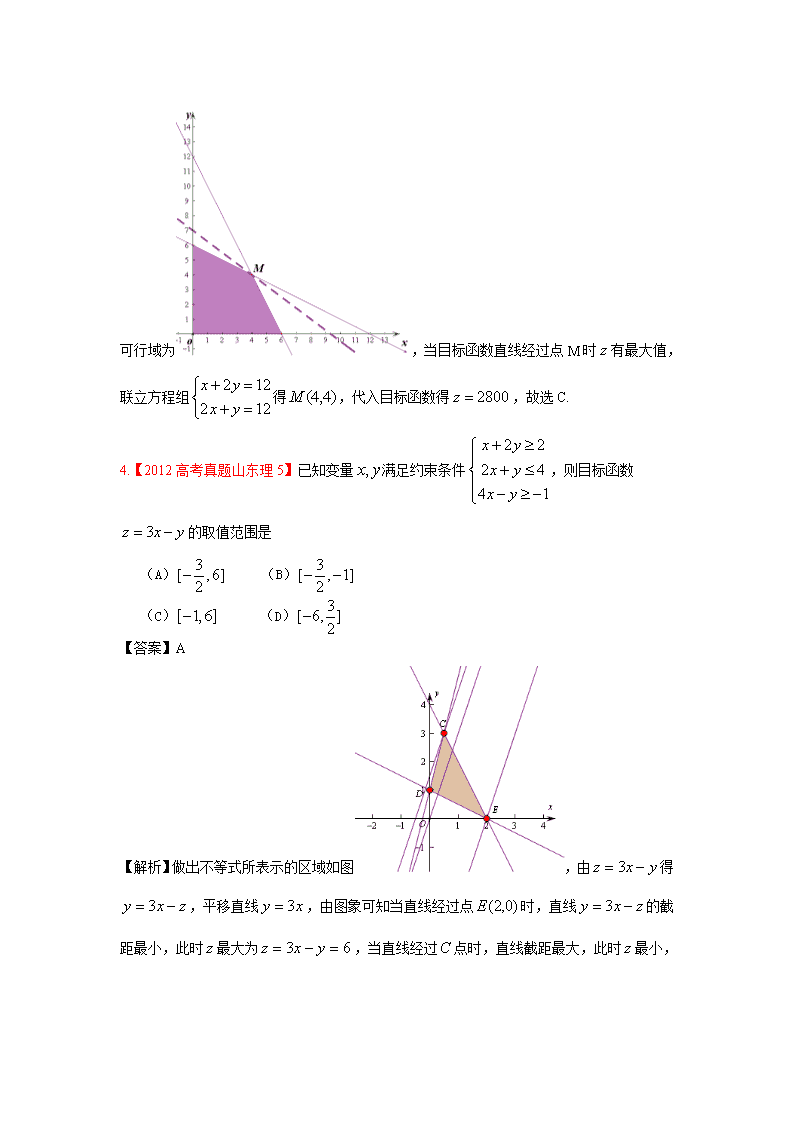
2012高考真题分类汇编:不等式 1.【2012高考真题重庆理2】不等式的解集为 A. B. C. D. 对 【答案】A 【解析】原不等式等价于或,即或,所以不等式的解为,选A. 2.【2012高考真题浙江理9】设a大于0,b大于0. A.若2a+2a=2b+3b,则a>b B.若2a+2a=2b+3b,则a>b C.若2a-2a=2b-3b,则a>b D.若2a-2a=ab-3b,则a<b 【答案】A 【解析】若,必有.构造函数:,则恒成立,故有函数在x>0上单调递增,即a>b成立.其余选项用同样方法排除.故选A 3.【2012高考真题四川理9】某公司生产甲、乙两种桶装产品。已知生产甲产品1桶需耗原料1千克、原料2千克;生产乙产品1桶需耗原料2千克,原料1千克。每桶甲产品的利润是300元,每桶乙产品的利润是400元。公司在生产这两种产品的计划中,要求每天消耗、原料都不超过12千克。通过合理安排生产计划,从每天生产的甲、乙两种产品中,公司共可获得的最大利润是( ) A、1800元 B、2400元 C、2800元 D、3100元 【答案】C. 【解析】设生产桶甲产品,桶乙产品,总利润为Z, 则约束条件为,目标函数为, 可行域为,当目标函数直线经过点M时有最大值,联立方程组得,代入目标函数得,故选C. 4.【2012高考真题山东理5】已知变量满足约束条件,则目标函数 的取值范围是 (A) (B) (C) (D) 【答案】A 【解析】做出不等式所表示的区域如图,由得,平移直线,由图象可知当直线经过点时,直线的截距最小,此时最大为,当直线经过点时,直线截距最大,此时 最小,由,解得,此时,所以的取值范围是,选A. 5.【2012高考真题辽宁理8】设变量x,y满足则的最大值为 (A) 20 (B) 35 (C) 45 (D) 55 【答案】D 【解析】画出可行域,根据图形可知当x=5,y=15时2x+3y最大,最大值为55,故选D 【点评】本题主要考查简单线性规划问题,难度适中。该类题通常可以先作图,找到最优解求出最值,也可以直接求出可行域的顶点坐标,代入目标函数进行验证确定出最值。 6.【2012高考真题广东理5】已知变量x,y满足约束条件,则z=3x+y的最大值为 A.12 B.11 C.3 D.-1 【答案】B 【解析】画约束区域如图所示,令得,化目标函数为斜截式方程得,当时,,故选B。 7.【2012高考真题福建理5】下列不等式一定成立的是 A. B. C. D. 【答案】C. 【解析】此类题目多选用筛选法,对于A当时,两边相等,故A错误;对于B具有基本不等式的形式,但是不一定大于零,故B错误;对于C,,显然成立;对于D任意都不成立.故选C. 8.【2012高考真题江西理8】某农户计划种植黄瓜和韭菜,种植面积不超过50计,投入资金不超过54万元,假设种植黄瓜和韭菜的产量、成本和售价如下表 年产量/亩 年种植成本/亩 每吨售价 黄瓜 4吨 1.2万元 0.55万元 韭菜 6吨 0.9万元 0.3万元 为使一年的种植总利润(总利润=总销售收入减去总种植成本)最大,那么黄瓜和韭菜的种植面积(单位:亩)分别为 A.50,0 B.30,20 C.20,30 D.0,50 【答案】B 【命题立意】本题考查函数的简单应用,以及简单的线性规划问题。 【解析】设黄瓜的种植面积为,韭菜的种植面积为,则有题意知,即,目标函数 ,作出可行域如图,由图象可知当直线经过点E时,直线的解决最大,此时取得最大值,由,解得,选B. 9.【2012高考真题湖北理6】设是正数,且, ,,则 A. B. C. D. 【答案】C 【解析】由于 等号成立当且仅当则a=t x b=t y c=t z , 所以由题知又,答案选C. 10.【2012高考真题福建理9】若函数y=2x图像上存在点(x,y)满足约束条件,则实数m的最大值为 A. B.1 C. D.2 【答案】B. 【解析】如图当直线经过函数的图像与直线的交点时,函数的图像仅有一个点在可行域内,有方程组得,所以,故选B. 11.【2012高考真题山东理13】若不等式的解集为,则实数__________. 【答案】 【解析】由可得,所以,所以,故。 12.【2012高考真题安徽理11】若满足约束条件:;则的取值范围为. 【答案】 【命题立意】本题考查线性规划知识,会求目标函数的范围。 【解析】约束条件对应边际及内的区域:,则。 13.【2012高考真题全国卷理13】若x,y满足约束条件则z=3x-y的最小值为_________. 【答案】 【解析】做出做出不等式所表示的区域如图,由得,平移直线,由图象可知当直线经过点时,直线的截距最 大,此时最小,最小值为. 14.【2012高考江苏13】(5分)已知函数的值域为,若关于x的不等式的解集为,则实数c的值为 ▲ . 【答案】9。 【考点】函数的值域,不等式的解集。 【解析】由值域为,当时有,即, ∴。 ∴解得,。 ∵不等式的解集为,∴,解得。 15.【2012高考江苏14】(5分)已知正数满足:则的取值范围是 ▲ . 【答案】。 【考点】可行域。 【解析】条件可化为: 。 设,则题目转化为: 已知满足,求的取值范围。 作出()所在平面区域(如图)。求出的切 线的斜率,设过切点的切线为, 则,要使它最小,须。 ∴的最小值在处,为。此时,点在上之间。 当()对应点时, , ∴的最大值在处,为7。 ∴的取值范围为,即的取值范围是。 16.【2012高考真题浙江理17】设aR,若x>0时均有[(a-1)x-1]( x 2-ax-1)≥0,则a=______________. 【答案】 【解析】本题按照一般思路,则可分为一下两种情况: (A), 无解; (B), 无解. 因为受到经验的影响,会认为本题可能是错题或者解不出本题.其实在x>0的整个区间上,我们可以将其分成两个区间(为什么是两个?),在各自的区间内恒正或恒负.(如下答图) 我们知道:函数y1=(a-1)x-1,y2=x 2-ax-1都过定点P(0,1). 考查函数y1=(a-1)x-1:令y=0,得M(,0),还可分析得:a>1; 考查函数y2=x 2-ax-1:显然过点M(,0),代入得:,解之得:,舍去,得答案:. 17.【2012高考真题新课标理14】 设满足约束条件:;则的取值范围为 【答案】 【解析】做出不等式所表示的区域如图,由得,平移直线,由图象可知当直线经过点时,直线的截距最小,此时最大为,当直线经过点时,直线截距最大,此时最小,由,解得,即,此时,所以,即的取值范围是.查看更多