三角函数知识点总结及高考题库学生版

三角函数知识点总结及高考题库学生版

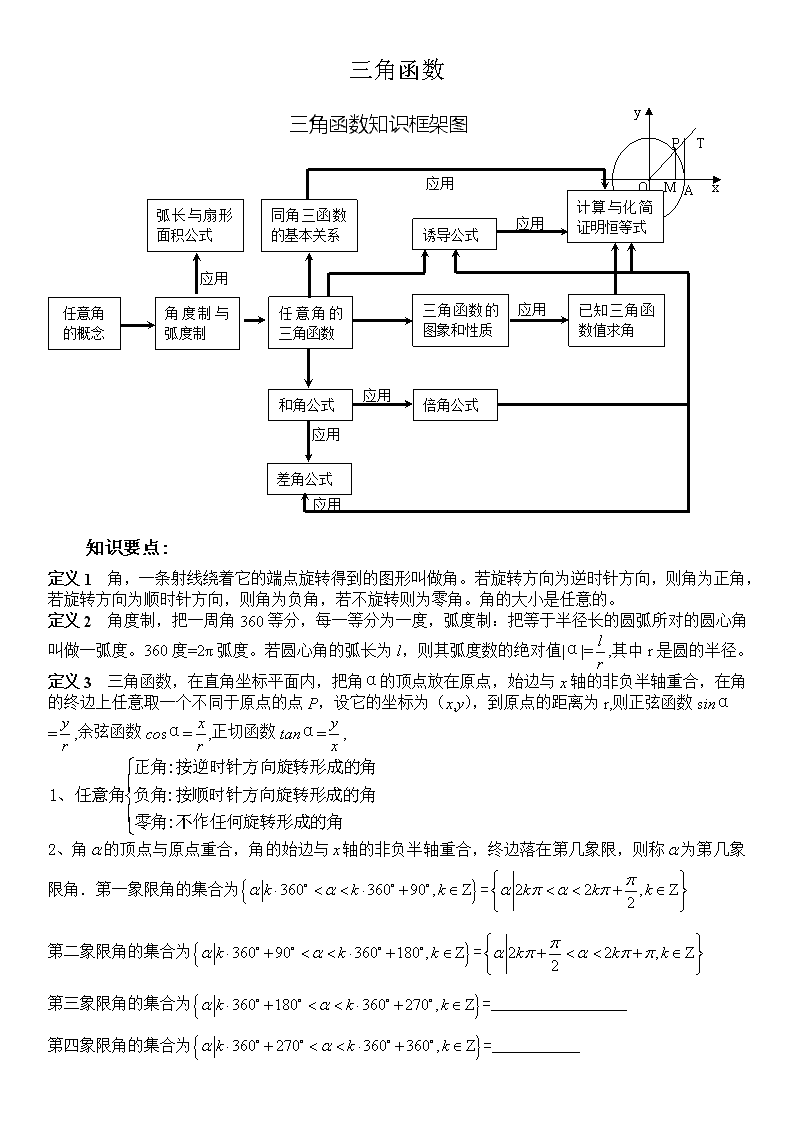
三角函数任意角的概念弧长与扇形面积公式角度制与弧度制同角三函数的基本关系任意角的三角函数诱导公式三角函数的图象和性质计算与化简证明恒等式已知三角函数值求角和角公式倍角公式差角公式应用应用应用应用应用应用应用三角函数知识框架图知识要点:定义1角，一条射线绕着它的端点旋转得到的图形叫做角。若旋转方向为逆时针方向，则角为正角，若旋转方向为顺时针方向，则角为负角，若不旋转则为零角。角的大小是任意的。定义2角度制，把一周角360等分，每一等分为一度，弧度制：把等于半径长的圆弧所对的圆心角叫做一弧度。360度=2π弧度。若圆心角的弧长为l，则其弧度数的绝对值|α|=,其中r是圆的半径。定义3三角函数，在直角坐标平面内，把角α的顶点放在原点，始边与x轴的非负半轴重合，在角的终边上任意取一个不同于原点的点P，设它的坐标为（x,y），到原点的距离为r,则正弦函数sinα=,余弦函数cosα=,正切函数tanα=,2、角的顶点与原点重合，角的始边与轴的非负半轴重合，终边落在第几象限，则称为第几象限角．第一象限角的集合为=第二象限角的集合为=第三象限角的集合为=_________________PvxyAOMT第四象限角的集合为=___________ 终边在轴上的角的集合为=____________________终边在轴上的角的集合为=_________________终边在坐标轴上的角的集合为=__________________3、与角终边相同的角的集合为=__________________4、已知是第几象限角，确定所在象限的方法：先把各象限均分等份，再从轴的正半轴的上方起，依次将各区域标上一、二、三、四，则原来是第几象限对应的标号即为终边所落在的区域．5、弧度制与角度制的换算公式：，，．6、若扇形的圆心角为，半径为，弧长为，周长为，面积为，则，，．7、三角函数在各象限的符号：第一象限全为正，第二象限正弦为正，第三象限正切为正，第四象限余弦为正．(口诀：一全正、二正弦、三正切、四余弦)8、三角函数线：，，．若，则sinx0）个单位，所得到的图象关于y轴对称，则m的最小正值是（D）A.B.C.D.9.函数f(x)=cosx(x)(xR)的图象按向量(m,0)平移后，得到函数y=-f′(x)的图象，则m的值可以为()A.B.C.－D.－10.若函数y=sin（x+）+2的图象按向量a平移后得到函数y=sinx的图象，则a等于（）A．（－，－2）B．（，2）C．（－，2）D．（，－2）11．将函数y=f（x）sinx的图象向右平移个单位，再作关于x轴的对称曲线，得到函数y=1－2sin2x的图象，则f（x）是（）A．cosxB．2cosxC．sinxD．2sinx12．若函数的图象按向量平移后，它的一条对称轴是，则的一个可能的值是A．B．C．D．13.将函数的图象按向量平移后所得的图象关于点中心对称，则向量的坐标可能为A．B．C．D．七.图象1．（07宁夏、海南卷）Ａ．Ｂ．Ｃ．Ｄ．函数在区间的简图是（　　） 2（浙江卷7）在同一平面直角坐标系中，函数的图象和直线的交点个数是（A）0（B）1（C）2（D）43.已知函数y=2sin(ωx+φ)(ω>0)在区间[0，2π]的图像如下：那么ω=（）A.1B.2C.1/2D.1/34．（2012年四川卷）下列函数中，图象的一部分如右图所示的是（）（A）（B）（C）（D）5.（2009宁夏海南卷文）已知函数的图像如图所示，则。6．为了得到函数y＝sin的图象，只需把函数y＝sin的图象(　　)A．向左平移个长度单位B．向右平移个长度单位C．向左平移个长度单位D．向右平移个长度单位7．已知函数y＝sincos，则下列判断正确的是(　　)A．此函数的最小正周期为2π，其图象的一个对称中心是B．此函数的最小正周期为π，其图象的一个对称中心是C．此函数的最小正周期为2π，其图象的一个对称中心是D．此函数的最小正周期为π，其图象的一个对称中心是8．如果函数y＝sin2x＋acos2x的图象关于直线x＝－对称，则实数a的值为(　　) A.　　　　　B．－C．1D．－19．(2010·福建)已知函数f(x)＝3sin(ω>0)和g(x)＝2cos(2x＋φ)＋1的图象的对称轴完全相同．若x∈，则f(x)的取值范围是________．10．设函数y＝cosπx的图象位于y轴右侧所有的对称中心从左依次为A1，A2，…，An，….则A50的坐标是________．11．把函数y＝cos的图象向左平移m个单位(m>0)，所得图象关于y轴对称，则m的最小值是________．12．已知函数f(x)＝Asin(x＋φ)(A＞0,0＜φ＜π)，x∈R的最大值是1，其图象经过点M.(1)求f(x)的解析式；(2)已知α，β∈，且f(α)＝，f(β)＝，求f(α－β)的值．14．(2010·山东)已知函数f(x)＝sin2xsinφ＋cos2xcosφ－sin(0<φ<π)，其图象过点.(1)求φ的值；(2)将函数y＝f(x)的图象上各点的横坐标缩短到原来的，纵坐标不变，得到函数y＝g(x)的图象，求函数g(x)在上的最大值和最小值．八.解三角形1.(2009年广东卷文)已知中，的对边分别为若且，则2.（2009湖南卷文）在锐角中，则的值等于2，的取值范围为.3.（09福建）已知锐角的面积为，，则角的大小为 4、在△ABC中，等于。5．已知△ABC中，，则的值为6.在中，，．（Ⅰ）求的值；（Ⅱ）设的面积，求的长．7.在中，角所对应的边分别为，，，求及8.已知向量m=(sinA,cosA),n=，m·n＝1，且A为锐角.（Ⅰ）求角A的大小；（Ⅱ）求函数的值域.9.在中，内角对边的边长分别是，已知，．（Ⅰ）若的面积等于，求；（Ⅱ）若，求的面积．九..综合1.（11年天津）定义在R上的函数既是偶函数又是周期函数，若的最小正周期是，且当 时，，则的值为2．(11年广东)函数f(x)是（）A．周期为的偶函数B．周期为的奇函数C．周期为2的偶函数D．.周期为2的奇函数3．（09四川）已知函数，下面结论错误的是()A.函数的最小正周期为2B.函数在区间［0，］上是增函数C.函数的图象关于直线＝0对称D.函数是奇函数4．(07安徽卷)函数的图象为C,如下结论中正确的是①图象C关于直线对称;②图象C关于点对称;③函数)内是增函数;④由的图象向右平移个单位长度可以得到图象C.5.（08广东卷）已知函数，则是（）A、最小正周期为的奇函数B、最小正周期为的奇函数C、最小正周期为的偶函数D、最小正周期为的偶函数6.在同一平面直角坐标系中，函数的图象和直线的交点个数是C（A）0（B）1（C）2（D）47．若α是第三象限角，且cos<0，则是（）A．第一象限角B．第二象限角C．第三象限角D．第四象限角8．已知函数对任意都有，则等于（）A、2或0B、或2C、0D、或0十.解答题1．（12福建文）已知.（Ⅰ）求的值；（Ⅱ）求的值. 2（11福建文）已知函数（I）求函数的最小正周期和单调增区间；（II）函数的图象可以由函数的图象经过怎样的变换得到？3．（2009年辽宁卷）已知函数，.求:(I)函数的最大值及取得最大值的自变量的集合；(II)函数的单调增区间.4.（10福建文）在中，，．（Ⅰ）求角的大小；（Ⅱ）若边的长为，求边的长．5.（08福建文）已知向量,且(Ⅰ)求tanA的值；(Ⅱ)求函数R)的值域.6.（2009福建卷文）已知函数其中，（I）若求的值；（Ⅱ）在（I）的条件下，若函数的图像的相邻两条对称轴之间的距离等于，求函数的解析式；并求最小正实数，使得函数的图像象左平移个单位所对应的函数是偶函数。 7.已知函数（）的最小正周期为．（Ⅰ）求的值；（Ⅱ）求函数在区间上的取值范围8.知函数（）的最小值正周期是．（Ⅰ）求的值；（Ⅱ）求函数的最大值，并且求使取得最大值的的集合．9.已知函数（Ⅰ）求函数的最小正周期和图象的对称轴方程（Ⅱ）求函数在区间上的值域10.已知函数f(x)＝为偶函数，且函数y＝f(x)图象的两相邻对称轴间的距离为（Ⅰ求f（）的值；（Ⅱ）将函数y＝f(x)的图象向右平移个单位后，再将得到的图象上各点的横坐标伸长到原来的4倍，纵坐标不变，得到函数y＝g(x)的图象，求g(x)的单调递减区间. 11.已知向量，，记函数。（1）求函数的最小正周期；（2）求函数的最大值，并求此时的值。12（09年重庆卷.文理17）求函数的最小正周期和最小值；并写出该函数在的单调递增区间.13.（2009湖北卷文）在锐角△ABC中，a、b、c分别为角A、B、C所对的边，且(Ⅰ)确定角C的大小：（Ⅱ）若c＝,且△ABC的面积为,求a＋b的值。14.（2012陕西卷文）已知函数（其中）的周期为，且图象上一个最低点为.(Ⅰ)求的解析式；（Ⅱ）当，求的最值.15.（2009北京文）（本小题共12分）已知函数.（Ⅰ）求的最小正周期；（Ⅱ）求在区间上的最大值和最小值. 16.（13全国二17）在中，，．（Ⅰ）求的值；（Ⅱ）设，求的面积．