中考数学试卷精选合辑之市初中毕业生学业考试试题及答案

中考数学试卷精选合辑之市初中毕业生学业考试试题及答案

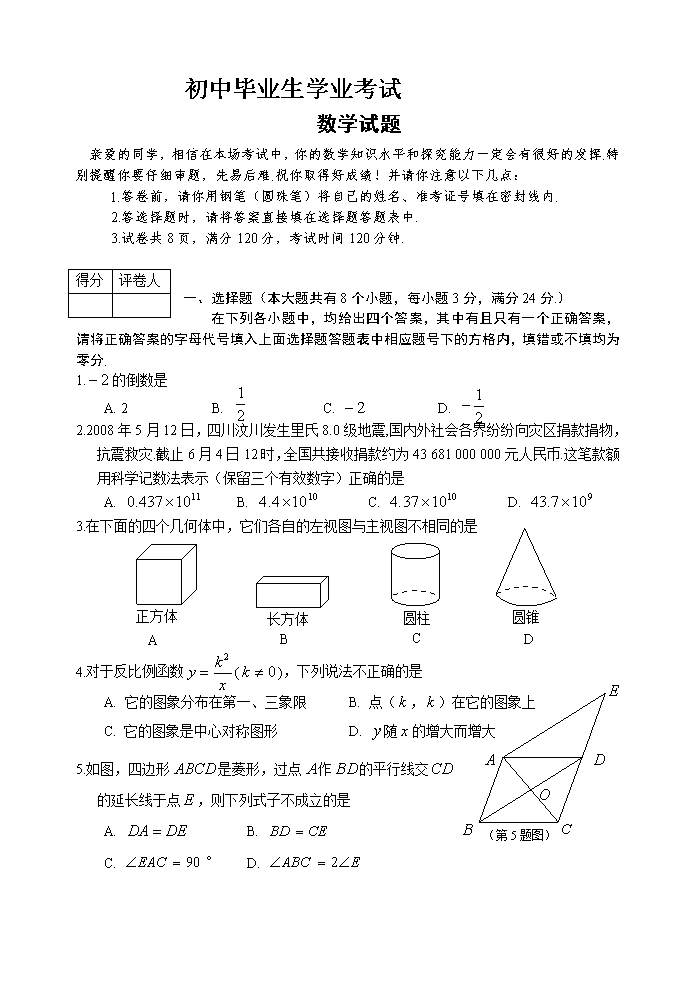
初中毕业生学业考试 数学试题 亲爱的同学，相信在本场考试中，你的数学知识水平和探究能力一定会有很好的发挥.特别提醒你要仔细审题，先易后难.祝你取得好成绩！并请你注意以下几点：‎ ‎1.答卷前，请你用钢笔（圆珠笔）将自己的姓名、准考证号填在密封线内.‎ ‎2.答选择题时，请将答案直接填在选择题答题表中.‎ ‎3.试卷共8页，满分120分，考试时间120分钟.‎ 得分 评卷人 一、选择题（本大题共有8个小题，每小题3分，满分24分.） ‎ 在下列各小题中，均给出四个答案，其中有且只有一个正确答案，请将正确答案的字母代号填入上面选择题答题表中相应题号下的方格内，填错或不填均为零分.‎ ‎1.的倒数是 A. 2 B. C. D. ‎ ‎2.‎2008年5月12日，四川汶川发生里氏8.0级地震,国内外社会各界纷纷向灾区捐款捐物，抗震救灾.截止‎6月4日12时，全国共接收捐款约为43 681 000 000元人民币.这笔款额用科学记数法表示（保留三个有效数字）正确的是 A. B. C. D. ‎ 正方体 长方体 圆柱 圆锥 A B C D ‎3.在下面的四个几何体中，它们各自的左视图与主视图不相同的是 ‎ ‎（第5题图）‎ ‎4.对于反比例函数()，下列说法不正确的是 A. 它的图象分布在第一、三象限 B. 点（，）在它的图象上 C. 它的图象是中心对称图形 D. 随的增大而增大 ‎ ‎5.如图，四边形是菱形，过点作的平行线交 的延长线于点，则下列式子不成立的是 A. B. ‎ ‎ C. ° D. ‎ ‎–1‎ ‎3‎ ‎3‎ ‎（第6题图）‎ ‎1‎ ‎6.如图，抛物线的对称轴是直线，且经过点（3，0），则的值为 ‎ A. 0 B. －‎1 C. 1 D. 2 ‎ ‎7.如图，三个大小相同的正方形拼成六边形，一动点 ‎ 从点出发沿着→→→→ 方向匀速运动，最后到 ‎ 达点.运动过程中的面积（）随时间（t）变化的图 象大致是 A B D C ‎（第7题图）‎ ‎.‎ ‎.‎ ‎.‎ ‎·‎ ‎60%‎ ‎8.如图，小明从半径为5的圆形纸片中剪下40%圆周的 ‎ 一个扇形，然后利用剪下的扇形制作成一个圆锥形玩具纸 帽‎40%‎ （接缝处不重叠），那么这个圆锥的高为 ‎（图2）‎ ‎（图1）‎ A.3 B‎.4 ‎C. D.‎ 得分 评卷人 ‎（第8题图）‎ 二、填空题（本大题共8个小题，每小题3分，满分24分）将结果直接填写在每题的横线上.‎ ‎9.分解因式：= .‎ ‎10.化简的结果是 .‎ ‎11. “五一”期间，某服装商店举行促销活动，全部商品八折销售.小华购买一件标价为180‎ 元的运动服，打折后他比按标价购买节省了 元.‎ ‎12. 关于的一元二次方程的一个根为1，则方程的另一根为 ‎ O ‎（第16题图）‎ ‎13.如图是我们生活中经常接触的小刀，‎ 刀柄外形是一个直角梯形（下底挖去一小半圆），刀片上、下是平行的，转动刀片时会形成∠1、∠2，则∠1+∠2＝ 度.‎ ‎……‎ ‎（第15题图）‎ ‎（第13题图）‎ ‎14.‎2008年6月2日，奥运火炬在荆州古城传递，208名火炬手参加了火炬传递，其中8位火炬手所跑的路程（单位：米）如下：60，70，100，60，80，70，90，100，则这组数据的中位数是 .‎ ‎15.如图，矩形的面积为5，它的两条对角线交于点，以、为两邻边作 平行四边形，平行四边形的对角线交于点，同样以、 ‎ 为两邻边作平行四边形，……，依次类推，则平行四边形的面积 为 . ‎ ‎16.如图，中，点的坐标为（0，1），点的坐标为（4，3），如果要使与 全等，那么点的坐标是 .‎ 得 分 评 卷 人 三、解答题（本大题共9个小题，满分72分.）‎ ‎17.(本题满分5分)‎ 计算：‎ 得 分 评 卷 人 ‎18.（本题满分5分）‎ 解不等式组 并把解集表示在下面的数轴上.‎ ‎0‎ ‎3‎ ‎2‎ ‎1‎ ‎－3‎ ‎－2‎ ‎－1‎ 得 分 评 卷 人 ‎19. （本题满分7分）‎ 为了降低能源消耗，减少环境污染，国务院办公厅下发了“关于限制生产销售使用塑料购物袋的通知”（简称“限塑令”），并从‎2008年6月1日起正式实施.小宇同学为了了解“限塑令”后使用购物袋的情况，‎6月8日到某集贸市场对部分购物者进行了调查，据了解该市场按塑料购物袋的承重能力提供了0.1元，0.2元，0.3元三种质量不同的塑料袋.下面两幅图是这次调查得到的不完整的统计图（若每人每次只使用一个购物袋），请你根据图中的信息，回答下列问题：‎ ‎（1）这次调查的购物者总人数是 ；‎ ‎（2）请补全条形统计图，并说明扇形统计图中元部分所对应的圆心角是 度0.3元部分所对应的圆心角是 度；‎ ‎（3）若‎6月8日到该市场购物的人数有3000人次，则该市场需销售塑料购物袋多少个？‎ 类别 ‎10‎ ‎20‎ ‎30‎ ‎40‎ ‎50‎ ‎0‎ 人数 ‎45‎ ‎33‎ ‎12‎ 自备 ‎0.1元 ‎0.2元 ‎0.3元 并根据调查情况，谈谈你的看法.‎ ‎0.1元 ‎135°‎ 自备 ‎90°‎ ‎0.2元 ‎0.3元 得 分 评 卷 人 ‎20.（本题满分7分）‎ 在数学活动课上，九年级（1）班数学兴趣小组的同学们测量 ‎ 校园内一棵大树的高度，设计的方案及测量数据如下：‎ ‎（1）在大树前的平地上选择一点，测得由点A看大树顶端的仰角为35°；‎ ‎（2）在点和大树之间选择一点（、、在同一直线上），测得由点看大树顶端的仰角恰好为45°；‎ ‎（3）量出、两点间的距离为‎4.5米.‎ 请你根据以上数据求出大树的高度.‎ ‎（可能用到的参考数据：sin35°≈0.57 cos35°≈0.82 tan35°≈0.70）‎ 得 分 评 卷 人 ‎21. （本题满分8分）‎ 箱中装有3张相同的卡片，它们分别写有数字1，2，4；箱中 也装有3张相同的卡片，它们分别写有数字2，4，5；现从箱、箱中各随机 地取出1张卡片，请你用画树形（状）图或列表的方法求：‎ ‎（1）两张卡片上的数字恰好相同的概率.‎ ‎（2）如果取出箱中卡片上的数字作为十位上的数字，取出箱中卡片上的数字作为个位上的数字，求两张卡片组成的两位数能被3整除的概率. ‎ 得 分 评 卷 人 ‎22. （本题满分8分）‎ 如图，为半圆的直径，点C在半圆上，过点作的平行线交于点，交过点的直线于点，且.‎ ‎（1）求证：是半圆O的切线；‎ ‎（2）若，，求的长.‎ 得 分 评 卷 人 ‎23. （本题满分10分）‎ 小华将一张矩形纸片（如图1）沿对角线剪开，得到两张三角形纸片（如图2），其中，然后将这两张三角形纸片按如图3所示的位置摆放，纸片的直角顶点落在纸片的斜边上，直角边落在所在的直线上.‎ （1） 若与相交于点，取的中点，连接、，当纸片沿方向平移时（如图3），请你观察、测量、的长度，猜想并写出与的数量关系，然后证明你的猜想；‎ （2） 在（1）的条件下，求出的大小（用含的式子表示），并说明当°时， 是什么三角形？‎ 图1‎ 图2‎ （3） 在图3的基础上，将纸片绕点逆时针旋转一定的角度（旋转角度小于90°），此时变成，同样取的中点，连接、（如图4），请继续探究与的数量关系和的大小，直接写出你的猜想，不需要证明，并说明为何值时，为等边三角形.‎ 图4‎ 图3‎ ‎ ‎ 得 分 评 卷 人 ‎24.（本题满分10分）‎ 华宇公司获得授权生产某种奥运纪念品，经市场调查分析，该纪念品的销售量（万件）与纪念品的价格（元／件）之间的函数图象如图所示，该公司纪念品的生产数量（万件）与纪念品的价格（元／件）近似满足函数关系式.，若每件纪念品的价格不小于20元，且不大于40元.请解答下列问题：‎ （1） 求与的函数关系式，并写出的取值范围；‎ （2） 当价格为何值时，使得纪念品产销平衡（生产量与销售量相等）；‎ （3） 当生产量低于销售量时，政府常通过向公司补贴纪念品的价格差来提高生产量，促成新的产销平衡.若要使新的产销平衡时销售量达到46万件，政府应对该纪念品每件补贴多少元？‎ ‎10‎ ‎20‎ ‎30‎ ‎40‎ ‎50‎ ‎0‎ ‎（元／件）‎ ‎（万件）‎ ‎10‎ ‎20‎ ‎30‎ ‎40‎ ‎60‎ ‎ ‎ 得 分 评 卷 人 ‎25.（本题满分12分）‎ 如图，直角梯形中，∥,为坐标原点，点在轴正半轴上，点在轴正半轴上，点坐标为（2，2），∠= 60°，于点.动点从点出发，沿线段向点运动，动点从点出发，沿线段向点运动，两点同时出发，速度都为每秒1个单位长度.设点运动的时间为秒.‎ （1） 求的长；‎ （2） 若的面积为（平方单位）. 求与之间的函数关系式.并求为何值时，的面积最大，最大值是多少？‎ （3） 设与交于点.①当△为等腰三角形时，求（2）中的值.‎ ‎ ②探究线段长度的最大值是多少，直接写出结论.‎ 参考答案及评分标准 说明：本试卷中的解答题一般只给出一种解法，对于其它解法，只要推理严谨、运算合理、结果正确，均给满分.对部分正确的，参照本评分说明酌情给分. ‎ 一、选择题（每小题3分，共24分） 1—8 D C B D B A B C 二、填空题（每小题3分，共24分）‎ ‎9. 10. 11. 36 12. ‎ ‎13. 90 14. 75 15. 16. ‎ ‎ （第14题不写单位不扣分）‎ 三、解答题（共72分）‎ ‎17.（5分）解：原式= ………………………………………………（3分）‎ ‎ ‎ ‎ =………………………………………………………………（5分）‎ ‎18.（5分）解：的解集是：‎ ‎ 的解集是：‎ ‎ 所以原不等式的解集是：………………………………………（3分）‎ 解集表示如图…………………………………………………………………（5分）‎ ‎·‎ ‎。‎ ‎ ‎ ‎ ‎ ‎19.（7分）解：（1）120……………………………………………………………………（1分）‎ ‎（2）条形统计图，如图所示，…………………………………………………… (2分)‎ 类别 ‎10‎ ‎20‎ ‎30‎ ‎40‎ ‎50‎ ‎0‎ 人数 ‎45‎ ‎33‎ ‎12‎ 自备 ‎0.1元 ‎0.2元 ‎0.3元 ‎0.2元的圆心角是99°，0.3元的圆心 ‎ 角是36°…………………（4分）‎ ‎（3）该市场需销售塑料购物袋的个数是 ‎ ‎………………（6分）‎ 只要谈的看法涉及环保、节能等方面，‎ 且观念积极向上，即可给分……（7分）‎ ‎20.（7分）（1）解：在中，‎ 在中，‎ 而 即…………………………………………（5分）‎ 解得：‎ 所以大树的高为米………………………………………………（7分）‎ ‎21.（8分）解：（1）由题意可列表：‎ ‎1‎ ‎2‎ ‎4‎ ‎2‎ ‎（1，2）‎ ‎（2，2）‎ ‎（4，2）‎ ‎4‎ ‎（1，4）‎ ‎（2，4）‎ ‎（4，4）‎ ‎5‎ ‎（1，5）‎ ‎（2，5）‎ ‎（4，5）‎ A B ‎ ‎ ‎ ∴两张卡片上的数字恰好相同的概率是.………………………（4分）‎ ‎ （2）由题意可列表：‎ ‎1‎ ‎2‎ ‎4‎ ‎2‎ ‎12‎ ‎22‎ ‎42‎ ‎4‎ ‎14‎ ‎24‎ ‎44‎ ‎5‎ ‎15‎ ‎25‎ ‎45‎ A B ‎∴两张卡片组成的两位数能被3整除的概率是………………（8分）‎ ‎（画树状图略）‎ ‎22.（8分）（1）证明：∵为半⊙的直径 ‎∴ ‎ 又∵∥， ∴‎ ‎∴ 而 ‎∴‎ ‎∴是半圆O的切线………………………………………………（3分）‎ ‎ （2）∵ ∴‎ ‎ 在中，…（5分）‎ ‎ 由∽可得：‎ ‎ 即 ‎∴…………………………………………………………（8分）‎ ‎23. （10分）解：（1）=………………………………………………………（1分）‎ ‎ 证明：∵的中点为 ∴在中， ‎ ‎ 在中，‎ ‎∴=………………………………………………（3分）‎ ‎（2）∵‎ ‎ 同理 ‎ ∴==‎ ‎ 而 ‎∴…………………………………………（6分）‎ ‎ ∴当时，，此时为等腰直角三角形.…（8分）‎ ‎ （3）当绕点逆时针旋转一定的角度，仍然存在=， ‎ ‎ ………………………………………………（9分）‎ ‎ 故当时，为等边三角形.…………………………（10分）‎ ‎24. （10分）解：（1）设与的函数解析式为：，将点、 代入得：‎ ‎ ‎ ‎ 解得：‎ ‎ ∴与的函数关系式为：……（3分）‎ ‎ （2）当时，有 ‎ 解得：……………………………………………………（5分）‎ ‎ 当时，有解得：‎ ‎ ‎ ‎ ∴当价格为30元或38元，可使公司产销平衡.…………………（7分）‎ ‎ （3）当时，则，∴‎ 当时，则，∴ ‎ ‎ ∴‎ ‎ ∴政府对每件纪念品应补贴1元……………………………（10分）‎ ‎25.（12分）解：（1）∵∥‎ ‎ ∴ ‎ ‎ 在中， ,‎ ‎ ∴， ‎ ‎∴ 而 ‎ ∴为等边三角形 ‎ ∴…（3分）‎ ‎（2）∵‎ ‎∴ ‎ ‎∴‎ ‎= （）…………………………（6分）‎ 即 ‎∴当时，………………………………………（7分）‎ ‎（3）①若为等腰三角形，则：‎ ‎（i）若， ‎ ‎ ∴∥ ‎ ‎∴ 即 解得：‎ 此时………………………………（8分）‎ ‎（ii）若，‎ ‎ ∴‎ 过点作，垂足为，则有：‎ 即 解得：‎ 此时……………………………………（9分）‎ ‎（iii）若，‎ ‎∴∥‎ 此时在上，不满足题意.……………………………………………（10分）‎ ‎ ②线段长的最大值为……………………………………………………(12分)‎