中考试卷数学

中考试卷数学

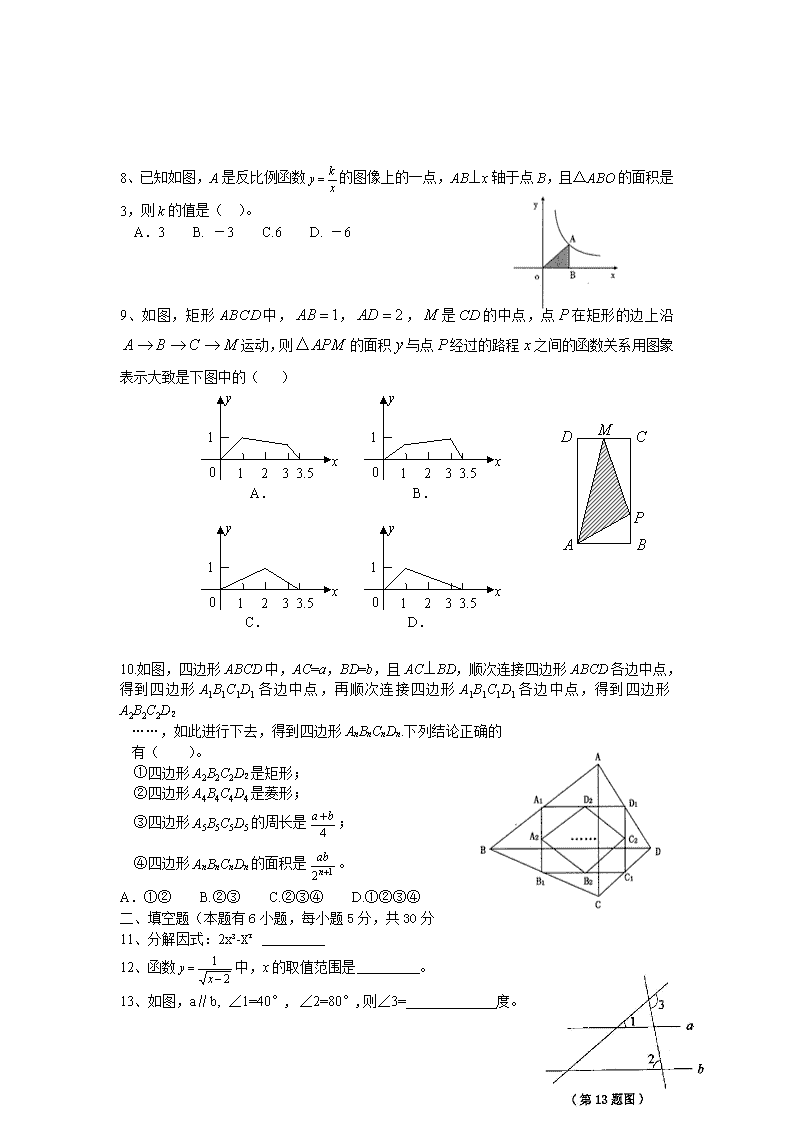
心之所向，所向披靡 ‎2011年金榜教育中考模拟试卷 ‎（满分：120分 考试时间：120 min）‎ 一、 选择题。（本题共40分，每小题4分）‎ ‎1、2－3的差的绝对值是（ ）。‎ ‎ A．1 B. －5 C.5 D. －1‎ ‎2、下列式子是分式的是（ ）。‎ ‎ A． B. C. D.‎ ‎3、已知点P（-1,4）在反比例函数的图像上，则k的值是（ ）‎ A、 B、 C、4 D、-4‎ ‎4、某班体育委员记录了第一小组七位同学定点投篮（每人投10个）的情况，投进篮框的个数分别为6 , 10 , 5 , 3 , 4 , 8 , 4 ，这组数据的中位数和极差分别是（ ）‎ A．4, 7 B．5, 7 C．7, 5 D．3, 7 ‎ ‎5、如图，在△ABC中，∠C=90°,AB=13，BC=5，则sinA的值是（ ）‎ A、 B、 C、 D、‎ ‎6、如图，内接于圆，，，是圆E A B C D O 的直径， 交于点，连结，则等于 A． B． C． D． ‎ ‎7、二次函数y=ax2+bx+c的图像如图所示，则关于此二次函数的下列四个结论①a<0②a>0③b2-4ac>0④中，正确的结论有（ ）‎ A.1个 B.2个 C.3个 D.4个 ‎8、已知如图，A是反比例函数的图像上的一点，AB⊥x轴于点B，且△ABO的面积是3，则k的值是（ ）。 ‎ ‎ A．3 B. －3 C.6 D. －6‎ ‎9、如图，矩形中，，，是的中点，点在矩形的边上沿运动，则的面积与点经过的路程之间的函数关系用图象表示大致是下图中的（ ）‎ ‎1‎ ‎1‎ ‎2‎ ‎3‎ ‎3.5‎ x y ‎0‎ A．‎ ‎1‎ ‎1‎ ‎2‎ ‎3‎ ‎3.5‎ x y ‎0‎ B．‎ ‎1‎ ‎1‎ ‎2‎ ‎3‎ ‎3.5‎ x y ‎0‎ ‎1‎ ‎1‎ ‎2‎ ‎3‎ ‎3.5‎ x y ‎0‎ ‎ ‎ D．‎ C．‎ ‎10.如图，四边形ABCD中，AC=a，BD=b，且AC⊥BD，顺次连接四边形ABCD各边中点，得到四边形A1B1C1D1各边中点，再顺次连接四边形A1B1C1D1各边中点，得到四边形A2B2C2D2‎ ‎……，如此进行下去，得到四边形AnBnCnDn.下列结论正确的 有（ ）。‎ ‎ ①四边形A2B2C2D2是矩形；‎ ‎ ②四边形A4B4C4D4是菱形；‎ ‎ ③四边形A5B5C5D5的周长是；‎ ‎ ④四边形AnBnCnDn的面积是。 ‎ A．①② B.②③ C.②③④ D.①②③④‎ 二、填空题（本题有6小题，每小题5分，共30分 ‎11、分解因式：2x³-X² ‎ ‎12、函数中，x的取值范围是 。‎ ‎13、如图，a∥b, ∠1=40°, ∠2=80°,则∠3= 度。‎ ‎14、如图，点A、B、C在直径为的⊙O上，∠BAC=45°，则图中阴影部分的面积等于 。（结果中保留）。‎ ‎15、.如图，在平面直角坐标系中有一矩形ABCD，其中A（0,0），B（8,0），D（0,4），若将△ABC沿AC所在直线翻折，点B落在E点处。则E点的坐标是 。‎ ‎（第14题） （第15题）‎ ‎16、我国汉代数学家赵爽为了证明勾股定理，创制了一副“弦图”，后人称其为“赵爽弦图”（如图1）。图2由弦图变化得到，它是由八个全等的直角三角形拼接而成。记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为，若=10，则的值是 。‎ 三、解答题 (本题有8小题,共66分,各小题都必须写出解答过程)‎ ‎17.(本题4分) ‎ 计算:‎ ‎18、解不等式 ,并把它的解集在数轴上表示出来.（本题4分）‎ ‎19、已知，求代数式的值．(本题4分)‎ ‎20、（8分）如图7所示，在△ABC中，AB=CB，∠ABC=90°，F为AB延长线上一点，点E在BC上，且AE=CF。‎ ‎ （1）求证：Rt△ABE≌△CBE；‎ ‎ （2）若∠CAE=30°，求∠ACF的度数。‎ ‎21、（8分）学校为了学生的身体健康，每天开展体育活动一小时，开设排球、篮球、羽毛球、体操课．学生可根据自己的爱好任选其中一项，老师根据学生报名情况进行了统计，并绘制了右边尚未完成的扇形统计图和频数分布直方图，请你结合图中的信息，解答下列问题：‎ ‎（1）该校学生报名总人数有多少人？　　‎ ‎（2）从表中可知选羽毛球的学生有多少人？选排球和篮球的人数分别占报名总人数的百分之几？　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　‎ ‎（3）将两个统计图补充完整．　　　　　　　　　　　　　　　　　　　　　 ‎ 羽毛球 ‎25%‎ 体操40%‎ ‎23、(10分)在平面直角坐标系中，如图1，将个边长为1的正方形并排组成矩形OABC, 相邻两边OA和OC分别落在轴和轴的正半轴上, 设抛物线（＜0）过矩形顶点B、C.‎ ‎（1）当n=1时，如果=-1，试求b的值；‎ ‎（2）当n=2时，如图2，在矩形OABC上方作一边长为1的正方形EFMN，使EF在线段CB上，如果M，N两点也在抛物线上，求出此时抛物线的解析式；‎ 图1 图2 图3‎ x y M N x O C E A B F A B y C O ‎…‎ x O y A C B ‎（3）将矩形OABC绕点O顺时针旋转，使得点B落到轴的正半轴上，如果该抛物线同时经过原点O.①试求当n=3时a的值；‎ ‎②直接写出关于的关系式．‎ ‎24.(本题12分)‎ 第24题图 O B D E C F x y A 如图，在平面直角坐标系中，点A（10，0），以OA为直径在第一象限内作半圆C，点B是该半圆周上一动点，连结OB、AB，并延长AB至点D，使DB=AB，过点D作x轴垂线，分别交x轴、直线OB于点E、F，点E为垂足，连结CF．‎ ‎（1）当∠AOB=30°时，求弧AB的长度； ‎ ‎（2）当DE=8时，求线段EF的长；‎ ‎（3）在点B运动过程中，是否存在以点E、C、F 为顶点的三角形与△AOB相似，若存在，请求出此 时点E的坐标；若不存在，请说明理由．‎ 答案：‎ 一、选择题 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 A B D B A C C C A C 一、 填空题 ‎11、X²（2x-1）‎ ‎12、x＞2‎ ‎13、120‎ ‎14、0.75π-1.5‎ ‎15、(245 325)‎ ‎16、103‎ 三、解答题 ‎17、 ‎ ‎=‎ ‎=. ‎ ‎18、解：去分母，得 ‎ ‎ 去括号，得 ‎ 移项合并同类项，得 ‎ ‎ 系数化为1，得 ‎ ‎ 所以，此不等式的解集为 ，在数轴上表示如图所示 ‎19、由2x-1=3得x=2, ‎ 又==， ‎ ‎∴当x=2时，原式=14. …2分 ‎ ‎20、解（1）证明：∵∠ABC=90°，‎ ‎∴∠CBF=∠ABE=90°，‎ 在Rt△ABE和Rt△CBF中， ，‎ ‎∴Rt△ABE≌△Rt△CBF（HL）；‎ ‎（2）∵AB=BC，∠ABC=90°，‎ ‎∴∠CAB=∠ACB=45°，‎ 又∵∠BAE=∠CAB-∠CAE=45°-30°=15°，‎ 由（1）知：Rt△ABE≌Rt△CBF，‎ ‎∴∠BCF=∠BAE=15°，‎ ‎∴∠ACF=∠BCF+∠ACB=45°+15°=60°‎ ‎21、（1）由两个统计图可知该校报名总人数是（人）‎ ‎（2）选羽毛球的人数是（人）． ‎ 因为选排球的人数是100人，所以， ‎ 因为选篮球的人数是40人，所以， ‎ 即选排球、篮球的人数占报名的总人数分别是25%和10%‎ ‎（3）如图 ‎ ‎22、（1）由题意可知，抛物线对称轴为直线x=，‎ ‎∴,得x y O C E A B M N F b= 1； ‎ y x O C A B ‎（2）设所求抛物线解析式为，‎ 由对称性可知抛物线经过点B（2，1）和点M（，2）‎ ‎∴ 解得 ‎ ‎∴所求抛物线解析式为；‎ ‎（3）①当n=3时，OC=1，BC=3，‎ 设所求抛物线解析式为，‎ x y O A B C D 过C作CD⊥OB于点D，则Rt△OCD∽Rt△CBD，‎ ‎∴, ‎ 设OD=t，则CD=3t，‎ ‎∵， ‎ ‎∴， ∴,‎ ‎∴C（，）, 又 B（，0）， ‎ ‎∴把B 、C坐标代入抛物线解析式，得 ‎ 解得:a=； ‎ ‎②. ……2分 ‎23(本题12分)‎ ‎（1）连结BC,‎ ‎∵A（10，0）, ∴OA=10 ,CA=5,‎ ‎∵∠AOB=30°,‎ ‎∴∠ACB=2∠AOB=60°,‎ O B D E C F x y A ‎∴弧AB的长=; ‎ ‎（2）连结OD,‎ ‎∵OA是⊙C直径, ∴∠OBA=90°,‎ 又∵AB=BD,‎ ‎∴OB是AD的垂直平分线,‎ ‎∴OD=OA=10,‎ 在Rt△ODE中，‎ OE=,‎ ‎∴AE=AO－OE=10-6=4,‎ 由 ∠AOB=∠ADE=90°-∠OAB，∠OEF=∠DEA，‎ 得△OEF∽△DEA,‎ ‎∴,即，∴EF=3；‎ O B D F C E A x y ‎（3）设OE=x，‎ ‎①当交点E在O，C之间时，由以点E、C、F为顶点的三角 形与△AOB相似，有∠ECF=∠BOA或∠ECF=∠OAB，‎ 当∠ECF=∠BOA时，此时△OCF为等腰三角形，点E为OC 中点，即OE=，‎ ‎∴E1（，0）；‎ 当∠ECF=∠OAB时，有CE=5-x, AE=10-x，‎ ‎∴CF∥AB,有CF=,‎ ‎∵△ECF∽△EAD,‎ O B D F C E A x y ‎∴,即,解得：,‎ ‎∴E2（，0）;‎ ‎②当交点E在点C的右侧时，‎ ‎∵∠ECF＞∠BOA，‎ ‎∴要使△ECF与△BAO相似，只能使∠ECF=∠BAO，‎ O B D F C E A x y 连结BE，‎ ‎∵BE为Rt△ADE斜边上的中线，‎ ‎∴BE=AB=BD,‎ ‎∴∠BEA=∠BAO,‎ ‎∴∠BEA=∠ECF,‎ ‎∴CF∥BE, ∴,‎ ‎∵∠ECF=∠BAO, ∠FEC=∠DEA=Rt∠， ‎ ‎∴△CEF∽△AED, ∴,‎ 而AD=2BE, ∴,‎ 即, 解得, ＜0（舍去），‎ ‎∴E3（，0）;‎ ‎③当交点E在点O的左侧时，‎ ‎∵∠BOA=∠EOF＞∠ECF .‎ ‎∴要使△ECF与△BAO相似，只能使∠ECF=∠BAO O B D F C E A x y 连结BE，得BE==AB，∠BEA=∠BAO ‎∴∠ECF=∠BEA,‎ ‎∴CF∥BE,‎ ‎∴,‎ 又∵∠ECF=∠BAO, ∠FEC=∠DEA=Rt∠， ‎ ‎∴△CEF∽△AED, ∴，‎ 而AD=2BE, ∴,‎ ‎∴, 解得, ＜0（舍去）,‎ ‎∵点E在x轴负半轴上, ∴E4（，0）,‎ 综上所述：存在以点E、C、F为顶点的三角形与△AOB相似,此时点E坐标为：‎ ‎（，0）、（，0）、（，0）、（，0）．‎ 做人最好状态是懂得尊重，不管他人闲事，不晒自己优越，也不秀恩爱。你越成长越懂得内敛自持，这世界并非你一人存在。‎ ‎　　做人静默，不说人坏话，做好自己即可。不求深刻，只求简单。‎ ‎　　你活着不是只为讨他人喜欢，也不是为了炫耀你拥有的，没人在乎，更多人在看笑话。你变得优秀，你身边的环境也会优化。‎ ‎　　3. 从今天开始，帮自己一个忙，不再承受身外的目光，不必在意他人的评价，为自己活着。‎ ‎　　从今天开始，帮自己一个忙，做喜欢的事情，爱最亲近的人，想笑就大笑，想哭就痛哭，不再束缚情感的空间，让自己活得轻松些。‎ ‎　　4. 很多你觉得天大的事情，当你急切地向别人倾诉时，在别人眼中也是个小事，他最多不痛不痒呵呵地应和着。‎ ‎　　因为他不是你，他无法感知你那种激烈的情绪。直到有一天，你觉得无需再向别人提起，你就已经挽救了你自己。‎ ‎　　这世界上除了你自己，没谁可以真正帮到你。‎ ‎　　5, 我们总是带着面具走进爱情的，总想展示自己最优越的一面，你要接受一个人，不只是接受他的优越，而是看清了他的平凡普通却仍然去深爱。‎ ‎　　事实经常是：我们走着走着，就感觉对方变了，其实我们并没有变，我们只是走进对方最真实的地方，然后迷失了自己。‎ ‎　　6. 我捧你，你就是杯子，我放手，你就是玻璃渣子。无论是恋人还是朋友，珍惜在你每一次难过、伤心时都陪伴在你身边的人。‎ ‎　　珍惜经常和你开玩笑的人，说明你在这个人的心中肯定有一定的分量。 珍惜在你心情不好时第一个发现的人。‎ ‎　　7. 今天再大的事，到了明天就是小事；今年再大的事，到了明年就是故事；今生再大的事，到了来世就是传说。‎ ‎　　人生如行路，一路艰辛，一路风景。你目光所及，就是你的人生境界。‎ ‎　　总是看到比自己优秀的人，说明你正在走上坡路；总是看到不如自己的人，说明你正在走下坡路。与其埋怨，不如思变。‎ ‎　　8. 归零是一种积极的心态。所有的成败相对于前一秒都是一种过去。过去能支撑未来，却代替不了明天。‎ ‎　　学会归零，是一种积极面向未来的意识。把每一天的醒来都看作是一种新生，以婴儿学步的态度，认真用好睡眠以前的时刻。‎ ‎　　归零，让坏的不影响未来，让好的不迷惑现在。‎ ‎　　9. 总有一天，你会与那个对的人不期而遇：所谓的幸福，从来都是水到渠成的。‎ ‎　　它无法预估，更没有办法计算，唯一能做得是：在遇见之前保持相信，在相遇之后寂静享用。‎ 宁可怀着有所期待的心等待下去，也不愿去对岁月妥协，因为相信幸福也许会迟到，但不会缺席。‎ 做人最好状态是懂得尊重，不管他人闲事，不晒自己优越，也不秀恩爱。你越成长越懂得内敛自持，这世界并非你一人存在。‎ ‎　　做人静默，不说人坏话，做好自己即可。不求深刻，只求简单。‎ ‎　　你活着不是只为讨他人喜欢，也不是为了炫耀你拥有的，没人在乎，更多人在看笑话。你变得优秀，你身边的环境也会优化。‎ ‎　　3. 从今天开始，帮自己一个忙，不再承受身外的目光，不必在意他人的评价，为自己活着。‎ ‎　　从今天开始，帮自己一个忙，做喜欢的事情，爱最亲近的人，想笑就大笑，想哭就痛哭，不再束缚情感的空间，让自己活得轻松些。‎ ‎　　4. 很多你觉得天大的事情，当你急切地向别人倾诉时，在别人眼中也是个小事，他最多不痛不痒呵呵地应和着。‎ ‎　　因为他不是你，他无法感知你那种激烈的情绪。直到有一天，你觉得无需再向别人提起，你就已经挽救了你自己。‎ ‎　　这世界上除了你自己，没谁可以真正帮到你。‎ ‎　　5, 我们总是带着面具走进爱情的，总想展示自己最优越的一面，你要接受一个人，不只是接受他的优越，而是看清了他的平凡普通却仍然去深爱。‎ ‎　　事实经常是：我们走着走着，就感觉对方变了，其实我们并没有变，我们只是走进对方最真实的地方，然后迷失了自己。‎ ‎　　6. 我捧你，你就是杯子，我放手，你就是玻璃渣子。无论是恋人还是朋友，珍惜在你每一次难过、伤心时都陪伴在你身边的人。‎ ‎　　珍惜经常和你开玩笑的人，说明你在这个人的心中肯定有一定的分量。 珍惜在你心情不好时第一个发现的人。‎ ‎　　7. 今天再大的事，到了明天就是小事；今年再大的事，到了明年就是故事；今生再大的事，到了来世就是传说。‎ ‎　　人生如行路，一路艰辛，一路风景。你目光所及，就是你的人生境界。‎ ‎　　总是看到比自己优秀的人，说明你正在走上坡路；总是看到不如自己的人，说明你正在走下坡路。与其埋怨，不如思变。‎ ‎　　8. 归零是一种积极的心态。所有的成败相对于前一秒都是一种过去。过去能支撑未来，却代替不了明天。‎ ‎　　学会归零，是一种积极面向未来的意识。把每一天的醒来都看作是一种新生，以婴儿学步的态度，认真用好睡眠以前的时刻。‎ ‎　　归零，让坏的不影响未来，让好的不迷惑现在。‎ ‎　　9. 总有一天，你会与那个对的人不期而遇：所谓的幸福，从来都是水到渠成的。‎ ‎　　它无法预估，更没有办法计算，唯一能做得是：在遇见之前保持相信，在相遇之后寂静享用。‎ ‎　　宁可怀着有所期待的心等待下去，也不愿去对岁月妥协，因为相信幸福也许会迟到，但不会缺席。‎