中考数学专题复习一填空选择综合题

中考数学专题复习一填空选择综合题

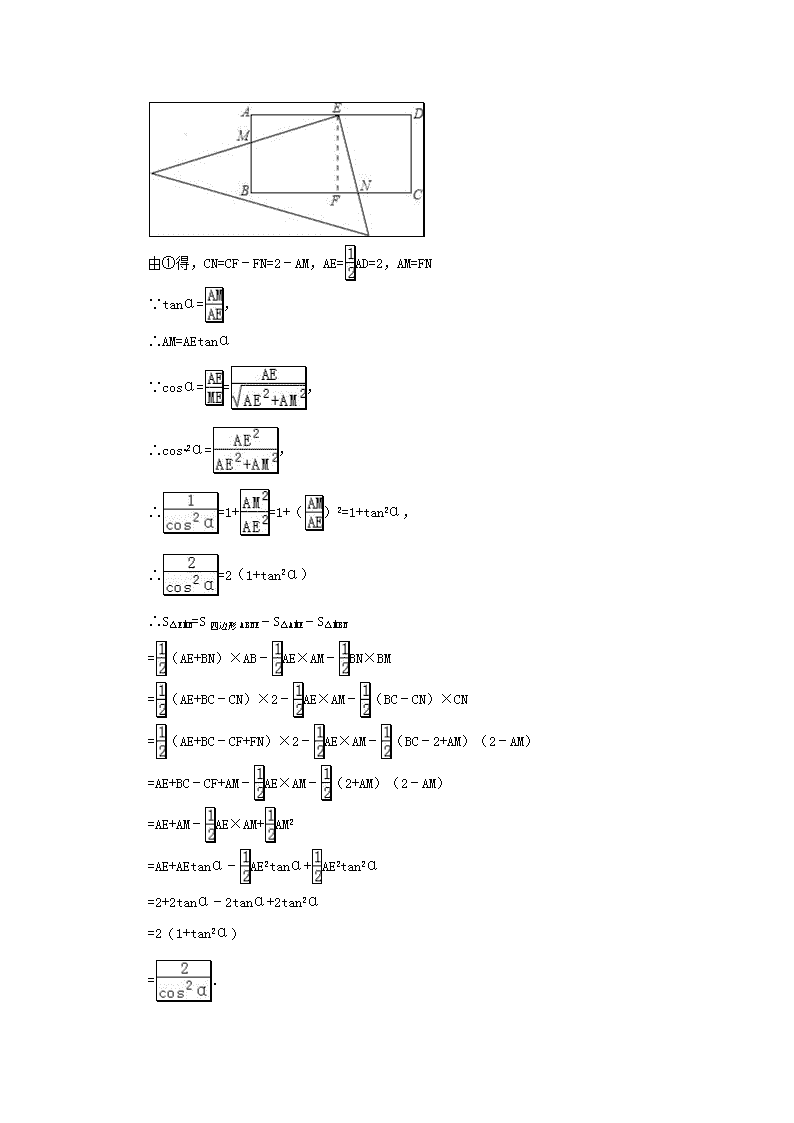
专题一：填空选择综合题 ‎【问题解析】‎ 选择题和填空题属于基础题，重在考查学生的基础知识和基本技能．但是为了更好地开发学生的智力，提高学生的能力，往往在选择题的最后一题或填空题的最后一题，设置一两道难度稍大的题目．这类题目类型可能是图形变化结合函数题、规律探究题、新定义题、剪切折叠问题等．还需要分类讨论，所以难度偏大．‎ ‎【热点探究】‎ 类型一： 涉及三角形综合问题 ‎【例题1】（2016·山东省德州市·3分）在矩形ABCD中，AD=2AB=4，E是AD的中点，一块足够大的三角板的直角顶点与点E重合，将三角板绕点E旋转，三角板的两直角边分别交AB，BC（或它们的延长线）于点M，N，设∠AEM=α（0°＜α＜90°），给出下列四个结论：‎ ‎①AM=CN；‎ ‎②∠AME=∠BNE；‎ ‎③BN﹣AM=2；‎ ‎④S△EMN=．‎ 上述结论中正确的个数是（　　）‎ A．1 B．‎2 ‎C．3 D．4‎ ‎【考点】全等三角形的判定与性质；旋转的性质．‎ ‎【分析】①作辅助线EF⊥BC于点F，然后证明Rt△AME≌Rt△FNE，从而求出AM=FN，所以BM与CN的长度相等．‎ ‎②由①Rt△AME≌Rt△FNE，即可得到结论正确；‎ ‎③经过简单的计算得到BN﹣AM=BC﹣CN﹣AM=BC﹣BM﹣AM=BC﹣（BM+AM）=BC﹣AB=4﹣2=2，‎ ‎④用面积的和和差进行计算，用数值代换即可．‎ ‎【解答】解：①如图，‎ 在矩形ABCD中，AD=2AB，E是AD的中点，‎ 作EF⊥BC于点F，则有AB=AE=EF=FC，‎ ‎∵∠AEM+∠DEN=90°，∠FEN+∠DEN=90°，‎ ‎∴∠AEM=∠FEN，‎ 在Rt△AME和Rt△FNE中，‎ ‎，‎ ‎∴Rt△AME≌Rt△FNE，‎ ‎∴AM=FN，‎ ‎∴MB=CN．‎ ‎∵AM不一定等于CN，‎ ‎∴AM不一定等于CN，‎ ‎∴①错误，‎ ‎②由①有Rt△AME≌Rt△FNE，‎ ‎∴∠AME=∠BNE，‎ ‎∴②正确，‎ ‎③由①得，BM=CN，‎ ‎∵AD=2AB=4，‎ ‎∴BC=4，AB=2‎ ‎∴BN﹣AM=BC﹣CN﹣AM=BC﹣BM﹣AM=BC﹣（BM+AM）=BC﹣AB=4﹣2=2，‎ ‎∴③正确，‎ ‎④如图，‎ 由①得，CN=CF﹣FN=2﹣AM，AE=AD=2，AM=FN ‎∵tanα=，‎ ‎∴AM=AEtanα ‎∵cosα==，‎ ‎∴cos2α=，‎ ‎∴=1+=1+（）2=1+tan2α，‎ ‎∴=2（1+tan2α）‎ ‎∴S△EMN=S四边形ABNE﹣S△AME﹣S△MBN ‎=（AE+BN）×AB﹣AE×AM﹣BN×BM ‎=（AE+BC﹣CN）×2﹣AE×AM﹣（BC﹣CN）×CN ‎=（AE+BC﹣CF+FN）×2﹣AE×AM﹣（BC﹣2+AM）（2﹣AM）‎ ‎=AE+BC﹣CF+AM﹣AE×AM﹣（2+AM）（2﹣AM）‎ ‎=AE+AM﹣AE×AM+AM2‎ ‎=AE+AEtanα﹣AE2tanα+AE2tan2α ‎=2+2tanα﹣2tanα+2tan2α ‎=2（1+tan2α）‎ ‎=．‎ ‎∴④正确．‎ 故选C．‎ ‎【点评】此题是全等三角形的性质和判定题，主要考查了全等三角形的性质和判定，图形面积的计算锐角三角函数，解本题的关键是Rt△AME≌Rt△FNE，难点是计算S△EMN．‎ ‎【同步练】‎ ‎（2016·辽宁丹东·3分）如图，在△ABC中，AD和BE是高，∠ABE=45°，点F是AB的中点，AD与FE、BE分别交于点G、H，∠CBE=∠BAD．有下列结论：①FD=FE；②AH=2CD；③BC•AD=AE2；④S△ABC=4S△ADF．其中正确的有（　　）‎ A．1个B．2 个C．3 个D．4个 类型二：涉及四边形综合问题 ‎【例题2】（烟台市 2015 中考 -17）如图，矩形OABC的顶点A、C的坐标分别是（4，0）和（0，2），反比例函数y=（x＞0）的图象过对角线的交点P并且与AB，BC分别交于D，E两点，连接OD，OE，DE，则△ODE的面积为　　 ．‎ ‎【解析】：由A、C的坐标分别是（4，0）和（0，2），得到P（2，1），求得k=2，得到反比例函数的解析式为：y=，求出D（4，），E（1，2）于是问题可解．‎ ‎【解答】解：∵四边形OABC是矩形，‎ ‎∴AB=OC，BC=OA，‎ ‎∵A、C的坐标分别是（4，0）和（0，2），‎ ‎∴OA=4，OB=2，‎ ‎∵P是矩形对角线的交点，‎ ‎∴P（2，1），‎ ‎∵反比例函数y=（x＞0）的图象过对角线的交点P，‎ ‎∴k=2，‎ ‎∴反比例函数的解析式为：y=，‎ ‎∵D，E两点在反比例函数y=（x＞0）的图象的图象上，‎ ‎∴D（4，），E（1，2）‎ ‎∴S阴影=S矩形﹣S△AOD﹣S△COF﹣S△BDE=4×2﹣×2﹣×2﹣××3=．‎ 故答案为：． ‎ ‎【点评】本题考查了反比例函数系数k的几何意义，待定系数法求函数的解析式，矩形的性质三角形的面积的求法，掌握反比例函数系数k的几何意义是解题的关键．‎ ‎【同步练】‎ ‎（2016·黑龙江龙东·3分）如图，在正方形ABCD中，E、F分别为BC、CD的中点，连接AE，BF交于点G，将△BCF沿BF对折，得到△BPF，延长FP交BA延长线于点Q，下列结论正确的个数是（　　）‎ ‎①AE=BF；②AE⊥BF；③sin∠BQP=；④S四边形ECFG=2S△BGE．‎ A．4 B．‎3 C．2 D．1‎ 类型三：设计规律探索研究问题 ‎【例题3】（郴州市 2015 中考 -16）请观察下列等式的规律：‎ ‎，‎ ‎，，‎ ‎…‎ 则=　 　．‎ 思路分析：‎ 从题干中观察算式可知（为非0自然数），把算式拆分再抵消即可求解．‎ 解题过程：‎ 解：‎ ‎=+++…‎ ‎=‎ ‎=‎ ‎=‎ ‎=‎ 故答案为：．‎ 规律总结：‎ 本题的关键规律为（为非0自然数），通过观察，分析、归纳并发现其中的规律，并应用发现的规律解决问题．‎ ‎【同步练】‎ ‎（2016·山东省德州市·4分）如图，在平面直角坐标系中，函数y=2x和y=﹣x的图象分别为直线l1，l2，过点（1，0）作x轴的垂线交l2于点A1，过点A1作y轴的垂线交l2‎ 于点A2，过点A2作x轴的垂线交l2于点A3，过点A3作y轴的垂线交l2于点A4，…依次进行下去，则点A2017的坐标为　 　．‎ 类型四：设计图形变换综合问题 ‎【例题4】‎ ‎（2016·青海西宁·2分）如图，已知正方形ABCD的边长为3，E、F分别是AB、BC边上的点，且∠EDF=45°，将△DAE绕点D逆时针旋转90°，得到△DCM．若AE=1，则FM的长为　　．‎ ‎【考点】旋转的性质；全等三角形的判定与性质；正方形的性质．‎ ‎【分析】由旋转可得DE=DM，∠EDM为直角，可得出∠EDF+∠MDF=90°，由∠EDF=45°，得到∠MDF为45°，可得出∠EDF=∠MDF，再由DF=DF，利用SAS可得出三角形DEF与三角形MDF全等，由全等三角形的对应边相等可得出EF=MF；则可得到AE=CM=1，正方形的边长为3，用AB﹣AE求出EB的长，再由BC+CM求出BM的长，设EF=MF=x，可得出BF=BM﹣FM=BM﹣EF=4﹣x，在直角三角形BEF中，利用勾股定理列出关于x的方程，求出方程的解得到x的值，即为FM的长．‎ ‎【解答】解：∵△DAE逆时针旋转90°得到△DCM，‎ ‎∴∠FCM=∠FCD+∠DCM=180°，‎ ‎∴F、C、M三点共线，‎ ‎∴DE=DM，∠EDM=90°，‎ ‎∴∠EDF+∠FDM=90°，‎ ‎∵∠EDF=45°，‎ ‎∴∠FDM=∠EDF=45°，‎ 在△DEF和△DMF中，‎ ‎，‎ ‎∴△DEF≌△DMF（SAS），‎ ‎∴EF=MF，‎ 设EF=MF=x，‎ ‎∵AE=CM=1，且BC=3，‎ ‎∴BM=BC+CM=3+1=4，‎ ‎∴BF=BM﹣MF=BM﹣EF=4﹣x，‎ ‎∵EB=AB﹣AE=3﹣1=2，‎ 在Rt△EBF中，由勾股定理得EB2+BF2=EF2，‎ 即22+（4﹣x）2=x2，‎ 解得：x=，‎ ‎∴FM=．‎ 故答案为：．‎ ‎【同步练】‎ ‎（郴州市 2015 中考 -8）如图，在矩形ABCD中，AB=3，将△ABD沿对角线BD对折，得到△EBD，DE与BC交于点F，∠ADB=30°，则EF=（　　）‎ A． B． C． 3 D．‎ 类型五：涉及动态类综合问题 ‎【例题5】（烟台市 2015 中考 -18）如图，直线l：y=﹣x+1与坐标轴交于A，B两点，点M（m，0）是x轴上一动点，以点M为圆心，2个单位长度为半径作⊙M，当⊙M与直线l相切时，则m的值为　 　．‎ ‎【解析】根据直线ly=﹣x+1由x轴的交点坐标A（0，1），B（2，0），得到OA=1，OB=2，求出AB=；设⊙M与AB相切与C，连接MC，则MC=2，MC⊥AB，通过△BMO～△ABO，即可得到结果．‎ ‎【解答】解：在y=﹣x+1中，‎ 令x=0，则y=1，‎ 令y=0，则x=2，‎ ‎∴A（0，1），B（2，0），‎ ‎∴AB=；‎ 如图，设⊙M与AB相切与C，‎ 连接MC，则MC=2，MC⊥AB，‎ ‎∵∠MCB=∠AOB=90°，∠B=∠B，‎ ‎∴△BMO～△ABO，‎ ‎∴，即 ‎∴BM=2，‎ ‎∴OM=2﹣2，或OM=2+2．‎ ‎∴m=2﹣2或m=2+2．‎ 故答案为：2﹣2，2+2．‎ ‎ ‎ ‎【点评】本题考查了直线与圆的位置关系，一次函数的性质，相似三角形的判定和性质，注意分类讨论是解题的关键．‎ ‎【同步练】‎ ‎（枣庄市 2015 中考 -18）如图，在平面直角坐标系中，点A（0，4），B（3，0），连接AB，将△AOB沿过点B的直线折叠，使点A落在x轴上的点A′处，折痕所在的直线交y轴正半轴于点C，则直线BC的解析式为　 　．‎ 类型六：涉及二次函数综合问题 ‎【例题6】（枣庄市 2015中考 -12）如图是二次函数y=ax2+bx+c（a≠0）图象的一部分，对称轴为x=，且经过点（2，0），有下列说法：①abc＜0；②a+b=0；③4a+2b+c＜0；④若（0，y1），（1，y2）是抛物线上的两点，则y1=y2．上述说法正确的是（　　）‎ A．①②④ B．③④ C． ①③④ Ｄ．①② ‎ ‎【解析】本题考查了二次函数的图象和系数的关系的应用，故对于题①可根据抛物线开口方向、对称轴位置、抛物线与y轴交点位置求得a、b、c的符号；‎ 对于题②可根据对称轴求出b=﹣a；‎ 对于题③可以把x=2代入函数关系式，结合图象判断函数值与0的大小关系；‎ 对于题④可以求出点（0，y1）关于直线x=的对称点的坐标，根据对称轴即可判断y1和y2的大小．‎ ‎【解答】解：①∵二次函数的图象开口向下，‎ ‎∴a＜0，‎ ‎∵二次函数的图象交y轴的正半轴于一点，‎ ‎∴c＞0，‎ ‎∵对称轴是直线x=，‎ ‎∴，‎ ‎∴b=﹣a＞0，‎ ‎∴abc＜0．‎ 故①正确；‎ ‎②∵由①中知b=﹣a，‎ ‎∴a+b=0，‎ 故②正确；‎ ‎③把x=2代入y=ax2+bx+c得：y=4a+2b+c，‎ ‎∵抛物线经过点（2，0），‎ ‎∴当x=2时，y=0，即4a+2b+c=0．‎ 故③错误；‎ ‎④∵（0，y1）关于直线x=的对称点的坐标是（1，y1），‎ ‎∴y1=y2．‎ 故④正确；‎ 综上所述，正确的结论是①②④．‎ 故选：A ‎ ‎【点评】解决此类问题重点是熟练把握二次函数的图象和系数的关系的应用，并注意：当a＞0时，二次函数的图象开口向上，当a＜0时，二次函数的图象开口向下．‎ ‎【同步练】‎ ‎（2016·湖北随州·3分）二次函数y=ax2+bx+c（a≠0）的部分图象如图所示，图象过点（﹣1，0），对称轴为直线x=2，下列结论：（1）‎4a+b=0；（2）‎9a+c＞3b；（3）‎8a+7b+‎2c＞0；（4）若点A（﹣3，y1）、点B（﹣，y2）、点C（，y3）在该函数图象上，则y1＜y3＜y2；（5）若方程a（x+1）（x﹣5）=﹣3的两根为x1和x2，且x1＜x2，则x1＜﹣1＜5＜x2．其中正确的结论有（　　）‎ A．2个 B．3个 C．4个 D．5个 ‎【达标检测】‎ ‎1. （枣庄市 2014 中考 -18）图①所示的正方体木块棱长为6cm，沿其相邻三个面的对角线（图中虚线）剪掉一角，得到如图②的几何体，一只蚂蚁沿着图②的几何体表面从顶点A爬行到顶点B的最短距离为　 　cm．‎ ‎2. （2016·黑龙江齐齐哈尔·3分）如图，在边长为2的菱形ABCD中，∠A=60°，点M是AD边的中点，连接MC，将菱形ABCD翻折，使点A落在线段CM上的点E处，折痕交AB于点N，则线段EC的长为　 ．‎ ‎3. （2016·陕西·3分）如图，在正方形ABCD中，连接BD，点O是BD的中点，若M、N是边AD上的两点，连接MO、NO，并分别延长交边BC于两点M′、N′，则图中的全等三角形共有（　　）‎ A．2对 B．3对 C．4对 D．5对 ‎4. （2016·山东潍坊·3分）已知∠AOB=60°，点P是∠AOB的平分线OC上的动点，点M在边OA上，且OM=4，则点P到点M与到边OA的距离之和的最小值是　 ．‎ ‎5. （2016·广西桂林·3分）已知直线y=﹣x+3与坐标轴分别交于点A，B，点P在抛物线y=﹣ （x﹣ ）2+4上，能使△ABP为等腰三角形的点P的个数有（　　）‎ A．3个 B．4个 C．5个 D．6个 ‎6. （2016·云南省昆明市·4分）如图，在正方形ABCD中，AC为对角线，E为AB上一点，过点E作EF∥AD，与AC、DC分别交于点G，F，H为CG的中点，连接DE，EH，DH，FH．下列结论：‎ ‎①EG=DF；②∠AEH+∠ADH=180°；③△EHF≌△DHC；④若=，则3S△EDH=13S△DHC，其中结论正确的有（　　）‎ A．1个 B．2个 C．3个 D．4个 ‎7. （2016·四川攀枝花）如图，二次函数y=ax2+bx+c（a＞0）图象的顶点为D，其图象与x轴的交点A、B的横坐标分别为﹣1和3，则下列结论正确的是（　　）‎ A．‎2a﹣b=0‎ B．a+b+c＞0‎ C．‎3a﹣c=0‎ D．当a=时，△ABD是等腰直角三角形 ‎8. （2016·四川眉山·3分）如图，已知点A是双曲线在第三象限分支上的一个动点，连结AO并延长交另一分支于点B，以AB为边作等边三角形ABC，点C在第四象限内，且随着点A的运动，点C的位置也在不断变化，但点C始终在双曲线上运动，则k的值是　 ．‎ ‎ ‎ ‎【达标检测参考答案】‎ 类型一： 设计三角形综合问题 ‎【同步练】‎ ‎（2016·辽宁丹东·3分）如图，在△ABC中，AD和BE是高，∠ABE=45°，点F是AB的中点，AD与FE、BE分别交于点G、H，∠CBE=∠BAD．有下列结论：①FD=FE；②AH=2CD；③BC•AD=AE2；④S△ABC=4S△ADF．其中正确的有（　　）‎ A．1个B．2 个C．3 个D．4个 ‎【考点】相似三角形的判定与性质；全等三角形的判定与性质．‎ ‎【分析】由直角三角形斜边上的中线性质得出FD=AB，证明△ABE是等腰直角三角形，得出AE=BE，证出FE=AB，延长FD=FE，①正确；‎ 证出∠ABC=∠C，得出AB=AC，由等腰三角形的性质得出BC=2CD，∠BAD=∠CAD=∠CBE，由ASA证明△AEH≌△BEC，得出AH=BC=2CD，②正确；‎ 证明△ABD～△BCE，得出=，即BC•AD=AB•BE，再由等腰直角三角形的性质和三角形的面积得出BC•AD=AE2；③正确；‎ 由F是AB的中点，BD=CD，得出S△ABC=2S△ABD=4S△ADF．④正确；即可得出结论．‎ ‎【解答】解：∵在△ABC中，AD和BE是高，‎ ‎∴∠ADB=∠AEB=∠CEB=90°，‎ ‎∵点F是AB的中点，‎ ‎∴FD=AB，‎ ‎∵∠ABE=45°，‎ ‎∴△ABE是等腰直角三角形，‎ ‎∴AE=BE，‎ ‎∵点F是AB的中点，‎ ‎∴FE=AB，‎ ‎∴FD=FE，①正确；‎ ‎∵∠CBE=∠BAD，∠CBE+∠C=90°，∠BAD+∠ABC=90°，‎ ‎∴∠ABC=∠C，‎ ‎∴AB=AC，‎ ‎∵AD⊥BC，‎ ‎∴BC=2CD，∠BAD=∠CAD=∠CBE，‎ 在△AEH和△BEC中，，‎ ‎∴△AEH≌△BEC（ASA），‎ ‎∴AH=BC=2CD，②正确；‎ ‎∵∠BAD=∠CBE，∠ADB=∠CEB，‎ ‎∴△ABD～△BCE，‎ ‎∴=，即BC•AD=AB•BE，‎ ‎∵AE2=AB•AE=AB•BE，BC•AD=AC•BE=AB•BE，‎ ‎∴BC•AD=AE2；③正确；[来源:学科网]‎ ‎∵F是AB的中点，BD=CD，∴‎ S△ABC=2S△ABD=4S△ADF．④正确；‎ 故选：D．‎ 类型二：设计四边形综合问题 ‎【同步练】‎ ‎（2016·黑龙江龙东·3分）如图，在正方形ABCD中，E、F分别为BC、CD的中点，连接AE，BF交于点G，将△BCF沿BF对折，得到△BPF，延长FP交BA延长线于点Q，下列结论正确的个数是（　　）‎ ‎①AE=BF；②AE⊥BF；③sin∠BQP=；④S四边形ECFG=2S△BGE．‎ A．4 B．‎3 C．2 D．1‎ ‎【考点】四边形综合题．‎ ‎【分析】首先证明△ABE≌△BCF，再利用角的关系求得∠BGE=90°，即可得到①AE=BF；②AE⊥BF；△BCF沿BF对折，得到△BPF，利用角的关系求出QF=QB，解出BP，QB，根据正弦的定义即可求解；根据AA可证△BGE与△BCF相似，进一步得到相似比，再根据相似三角形的性质即可求解．‎ ‎【解答】解：∵E，F分别是正方形ABCD边BC，CD的中点，‎ ‎∴CF=BE，‎ 在△ABE和△BCF中，‎ ‎，‎ ‎∴Rt△ABE≌Rt△BCF（SAS），‎ ‎∴∠BAE=∠CBF，AE=BF，故①正确；‎ 又∵∠BAE+∠BEA=90°，‎ ‎∴∠CBF+∠BEA=90°，‎ ‎∴∠BGE=90°，‎ ‎∴AE⊥BF，故②正确；‎ 根据题意得，FP=FC，∠PFB=∠BFC，∠FPB=90°‎ ‎∵CD∥AB，‎ ‎∴∠CFB=∠ABF，‎ ‎∴∠ABF=∠PFB，‎ ‎∴QF=QB，‎ 令PF=k（k＞0），则PB=2k 在Rt△BPQ中，设QB=x，‎ ‎∴x2=（x﹣k）2+4k2，‎ ‎∴x=，‎ ‎∴sin=∠BQP==，故③正确；‎ ‎∵∠BGE=∠BCF，∠GBE=∠CBF，‎ ‎∴△BGE∽△BCF，‎ ‎∵BE=BC，BF=BC，‎ ‎∴BE：BF=1：，‎ ‎∴△BGE的面积：△BCF的面积=1：5，‎ ‎∴S四边形ECFG=4S△BGE，故④错误．‎ 故选：B．‎ 类型三：设计规律探索研究问题 ‎【同步练】‎ ‎（2016·山东省德州市·4分）如图，在平面直角坐标系中，函数y=2x和y=﹣x的图象分别为直线l1，l2，过点（1，0）作x轴的垂线交l2于点A1，过点A1作y轴的垂线交l2于点A2，过点A2作x轴的垂线交l2于点A3，过点A3作y轴的垂线交l2于点A4，…依次进行下去，则点A2017的坐标为　（21008，21009）　．‎ ‎【考点】一次函数图象上点的坐标特征．‎ ‎【专题】规律型；一次函数及其应用．‎ ‎【分析】写出部分An点的坐标，根据坐标的变化找出变化规律“A2n+1（（﹣2）n，2（﹣2）n）（n为自然数）”，依此规律即可得出结论．‎ ‎【解答】解：观察，发现规律：A1（1，2），A2（﹣2，2），A3（﹣2，﹣4），A4（4，﹣4），A5（4，8），…，‎ ‎∴A2n+1（（﹣2）n，2（﹣2）n）（n为自然数）．‎ ‎∵2017=1008×2+1，‎ ‎∴A2017的坐标为（（﹣2）1008，2（﹣2）1008）=（21008，21009）．‎ 故答案为：（21008，21009）．‎ ‎【点评】本题考查了一次函数图象上点的坐标特征以及规律型中坐标的变化，解题的关键是找出变化规律“A2n+1（（﹣2）n，2（﹣2）n）（n为自然数）”．本题属于基础题，难度不大，解决该题型题目时，写出部分An点的坐标，根据坐标的变化找出变化规律是关键．‎ 类型四：设计图形变换综合问题 ‎【同步练】‎ ‎（郴州市 2015 中考 -8）如图，在矩形ABCD中，AB=3，将△ABD沿对角线BD对折，得到△EBD，DE与BC交于点F，∠ADB=30°，则EF=（　　）‎ A． B． C． 3 D．‎ 思路分析：‎ 考查了翻折变换问题，我们利用翻折变换的性质得出：∠1=∠2=30°，进而结合锐角三角函数关系求出FE的长．‎ 解题过程：‎ 解：如图所示：由题意可得：∠1=∠2=30°，则∠3=30°，‎ 可得∠4=∠5=60°，‎ ‎∵AB=DC=BE=3，‎ ‎∴tan60°=，‎ 解得：EF=．‎ 故选：A．‎ 规律总结：‎ 解此类问题关键是抓住翻折变换的性质以及锐角三角函数关系，得出∠4=∠5=60°．‎ 类型五：涉及动态类综合问题 ‎【同步练】‎ ‎（枣庄市 2015 中考 -18）如图，在平面直角坐标系中，点A（0，4），B（3，0），连接AB，将△AOB沿过点B的直线折叠，使点A落在x轴上的点A′处，折痕所在的直线交y轴正半轴于点C，则直线BC的解析式为　 　．‎ ‎【解析】本题考查了折叠的性质和勾股定理的应用，在Rt△OAB中，OA=4，OB=3，可用勾股定理计算出AB=5，再根据折叠的性质得BA′=BA=5，CA′=CA，则OA′=BA′﹣OB=2，设OC=t，则CA=CA′=4﹣t，在Rt△OA′C中，根据勾股定理得到t2+22=（4﹣t）2，解得t=，则C点坐标为（0，），然后利用待定系数法确定直线BC的解析式．‎ ‎【解答】解：∵A（0，4），B（3，0），‎ ‎∴OA=4，OB=3，‎ 在Rt△OAB中，AB==5，‎ ‎∵△AOB沿过点B的直线折叠，使点A落在x轴上的点A′处，‎ ‎∴BA′=BA=5，CA′=CA，‎ ‎∴OA′=BA′﹣OB=5﹣3=2，‎ 设OC=t，则CA=CA′=4﹣t，‎ 在Rt△OA′C中，‎ ‎∵OC2+OA′2=CA′2，‎ ‎∴t2+22=（4﹣t）2，解得t=，‎ ‎∴C点坐标为（0，），‎ 设直线BC的解析式为y=kx+b，‎ 把B（3，0）、C（0，）代入得，解得，‎ ‎∴直线BC的解析式为．‎ 故答案为：． ‎ ‎【点评】本题的关键是把握住折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等并能灵活运用，同时也要把握勾股定理和待定系数法求一次函数解析式．‎ 类型六：涉及二次函数综合问题 ‎【同步练】‎ ‎（2016·湖北随州·3分）二次函数y=ax2+bx+c（a≠0）的部分图象如图所示，图象过点（﹣1，0），对称轴为直线x=2，下列结论：（1）‎4a+b=0；（2）‎9a+c＞3b；（3）‎8a+7b+‎2c＞0；（4）若点A（﹣3，y1）、点B（﹣，y2）、点C（，y3）在该函数图象上，则y1＜y3＜y2；（5）若方程a（x+1）（x﹣5）=﹣3的两根为x1和x2，且x1＜x2，则x1＜﹣1＜5＜x2．其中正确的结论有（　　）‎ A．2个 B．3个 C．4个 D．5个 ‎【考点】二次函数图象与系数的关系．‎ ‎【分析】（1）正确．根据对称轴公式计算即可．‎ ‎（2）错误，利用x=﹣3时，y＜0，即可判断．‎ ‎（3）正确．由图象可知抛物线经过（﹣1，0）和（5，0），列出方程组求出a、b即可判断．‎ ‎（4）错误．利用函数图象即可判断．‎ ‎（5）正确．利用二次函数与二次不等式关系即可解决问题．‎ ‎【解答】解：（1）正确．∵﹣ =2，‎ ‎∴‎4a+b=0．故正确．‎ ‎（2）错误．∵x=﹣3时，y＜0，‎ ‎∴‎9a﹣3b+c＜0，‎ ‎∴‎9a+c＜3b，故（2）错误．‎ ‎（3）正确．由图象可知抛物线经过（﹣1，0）和（5，0），‎ ‎∴解得，‎ ‎∴‎8a+7b+‎2c=‎8a﹣‎28a﹣‎10a=﹣‎30a，‎ ‎∵a＜0，‎ ‎∴‎8a+7b=‎2c＞0，故（3）正确．‎ ‎（4）错误，∵点A（﹣3，y1）、点B（﹣，y2）、点C（，y3），‎ ‎∵﹣2=，2﹣（﹣）=，‎ ‎∴＜‎ ‎∴点C离对称轴的距离近，‎ ‎∴y3＞y2，‎ ‎∵a＜0，﹣3＜﹣＜2，‎ ‎∴y1＜y2‎ ‎∴y1＜y2＜y3，故（4）错误．‎ ‎（5）正确．∵a＜0，‎ ‎∴（x+1）（x﹣5）=﹣3/a＞0，‎ 即（x+1）（x﹣5）＞0，‎ 故x＜﹣1或x＞5，故（5）正确．‎ ‎∴正确的有三个，‎ 故选B．‎ ‎【达标检测】‎ ‎1. （枣庄市 2014 中考 -18）图①所示的正方体木块棱长为6cm，沿其相邻三个面的对角线（图中虚线）剪掉一角，得到如图②的几何体，一只蚂蚁沿着图②的几何体表面从顶点A爬行到顶点B的最短距离为　 　cm．‎ ‎【解析】本题考查了平面展开﹣最短路径问题，要求蚂蚁爬行的最短距离，需将图②的几何体表面展开，进而根据“两点之间线段最短”得出结果．‎ ‎【解答】：如图所示：‎ ‎△BCD是等腰直角三角形，△ACD是等边三角形，‎ 在Rt△BCD中，CD==cm，‎ ‎∴BE=CD=cm，‎ 在Rt△ACE中，AE==cm，‎ ‎∴从顶点A爬行到顶点B的最短距离为（）cm．‎ 故答案为：（）． ‎ ‎【点评】解决本题的关键就是把图②的几何体表面展开成平面图形，根据等腰直角三角形的性质和等边三角形的性质解决问题．‎ ‎2. （2016·黑龙江齐齐哈尔·3分）如图，在边长为2的菱形ABCD中，∠A=60°，点M是AD边的中点，连接MC，将菱形ABCD翻折，使点A落在线段CM上的点E处，折痕交AB于点N，则线段EC的长为　﹣1　．‎ ‎【考点】翻折变换（折叠问题）；菱形的性质．‎ ‎【分析】过点M作MF⊥DC于点F，根据在边长为2的菱形ABCD中，∠A=60°，M为AD中点，得到2MD=AD=CD=2，从而得到∠FDM=60°，∠FMD=30°，进而利用锐角三角函数关系求出EC的长即可．‎ ‎【解答】解：如图所示：过点M作MF⊥DC于点F，‎ ‎∵在边长为2的菱形ABCD中，∠A=60°，M为AD中点，‎ ‎∴2MD=AD=CD=2，∠FDM=60°，‎ ‎∴∠FMD=30°，‎ ‎∴FD=MD=，‎ ‎∴FM=DM×cos30°=，‎ ‎∴MC==，‎ ‎∴EC=MC﹣ME=﹣1．‎ 故答案为：﹣1．‎ ‎3. （2016·陕西·3分）如图，在正方形ABCD中，连接BD，点O是BD的中点，若M、N是边AD上的两点，连接MO、NO，并分别延长交边BC于两点M′、N′，则图中的全等三角形共有（　　）‎ A．2对 B．3对 C．4对 D．5对 ‎【考点】正方形的性质；全等三角形的判定．‎ ‎【分析】可以判断△ABD≌△BCD，△MDO≌△M′BO，△NOD≌△N′OB，△MON≌△M′ON′由此即可对称结论．‎ ‎【解答】解：∵四边形ABCD是正方形，‎ ‎∴AB=CD=CB=AD，∠A=∠C=∠ABC=∠ADC=90°，AD∥BC，‎ 在△ABD和△BCD中，‎ ‎，‎ ‎∴△ABD≌△BCD，‎ ‎∵AD∥BC，‎ ‎∴∠MDO=∠M′BO，‎ 在△MOD和△M′OB中，‎ ‎，‎ ‎∴△MDO≌△M′BO，同理可证△NOD≌△N′OB，∴△MON≌△M′ON′，‎ ‎∴全等三角形一共有4对．‎ 故选C．‎ ‎4. （2016·山东潍坊·3分）已知∠AOB=60°，点P是∠AOB的平分线OC上的动点，点M在边OA上，且OM=4，则点P到点M与到边OA的距离之和的最小值是　2　．‎ ‎【考点】轴对称-最短路线问题．‎ ‎【分析】过M作MN′⊥OB于N′，交OC于P，即MN′的长度等于点P到点M与到边OA的距离之和的最小值，解直角三角形即可得到结论．‎ ‎【解答】解：过M作MN′⊥OB于N′，交OC于P，‎ 则MN′的长度等于PM+PN的最小值，‎ 即MN′的长度等于点P到点M与到边OA的距离之和的最小值，‎ ‎∵∠ON′M=90°，OM=4，‎ ‎∴MN′=OM•sin60°=2，‎ ‎∴点P到点M与到边OA的距离之和的最小值为2．‎ ‎5. （2016·广西桂林·3分）已知直线y=﹣x+3与坐标轴分别交于点A，B，点P在抛物线y=﹣ （x﹣ ）2+4上，能使△ABP为等腰三角形的点P的个数有（　　）‎ A．3个 B．4个 C．5个 D．6个 ‎【考点】二次函数图象上点的坐标特征；一次函数图象上点的坐标特征；等腰三角形的判定．‎ ‎【分析】以点B为圆心线段AB长为半径做圆，交抛物线于点C、M、N点，连接AC、BC，由直线y=﹣x+3可求出点A、B的坐标，结合抛物线的解析式可得出△ABC等边三角形，再令抛物线解析式中y=0求出抛物线与x轴的两交点的坐标，发现该两点与M、N重合，结合图形分三种情况研究△ABP为等腰三角形，由此即可得出结论．‎ ‎【解答】解：以点B为圆心线段AB长为半径做圆，交抛物线于点C、M、N点，连接AC、BC，如图所示．‎ 令一次函数y=﹣x+3中x=0，则y=3，‎ ‎∴点A的坐标为（0，3）；‎ 令一次函数y=﹣x+3中y=0，则﹣x+3，‎ 解得：x=，‎ ‎∴点B的坐标为（，0）．‎ ‎∴AB=2．‎ ‎∵抛物线的对称轴为x=，‎ ‎∴点C的坐标为（2，3），‎ ‎∴AC=2=AB=BC，‎ ‎∴△ABC为等边三角形．‎ 令y=﹣（x﹣）2+4中y=0，则﹣（x﹣）2+4=0，‎ 解得：x=﹣，或x=3．‎ ‎∴点E的坐标为（﹣，0），点F的坐标为（3，0）．‎ ‎△ABP为等腰三角形分三种情况：‎ ‎①当AB=BP时，以B点为圆心，AB长度为半径做圆，与抛物线交于C、M、N三点；‎ ‎②当AB=AP时，以A点为圆心，AB长度为半径做圆，与抛物线交于C、M两点，；‎ ‎③当AP=BP时，作线段AB的垂直平分线，交抛物线交于C、M两点；‎ ‎∴能使△ABP为等腰三角形的点P的个数有3个．‎ 故选A．‎ ‎6. （2016·云南省昆明市·4分）如图，在正方形ABCD中，AC为对角线，E为AB上一点，过点E作EF∥AD，与AC、DC分别交于点G，F，H为CG的中点，连接DE，EH，DH，FH．下列结论：‎ ‎①EG=DF；②∠AEH+∠ADH=180°；③△EHF≌△DHC；④若=，则3S△EDH=13S△DHC，其中结论正确的有（　　）‎ A．1个 B．2个 C．3个 D．4个 ‎【考点】正方形的性质；全等三角形的判定与性质．‎ ‎【分析】①根据题意可知∠ACD=45°，则GF=FC，则EG=EF﹣GF=CD﹣FC=DF；‎ ‎②由SAS证明△EHF≌△DHC，得到∠HEF=∠HDC，从而∠AEH+∠ADH=∠AEF+∠HEF+∠ADF﹣∠HDC=180°；‎ ‎③同②证明△EHF≌△DHC即可；‎ ‎④若=，则AE=2BE，可以证明△EGH≌△DFH，则∠EHG=∠DHF且EH=DH，则∠DHE=90°，△EHD为等腰直角三角形，过H点作HM垂直于CD于M点，设HM=x，则DM=5x，DH=x，CD=6x，则S△DHC=×HM×CD=3x2，S△EDH=×DH2=13x2．‎ ‎【解答】解：①∵四边形ABCD为正方形，EF∥AD，‎ ‎∴EF=AD=CD，∠ACD=45°，∠GFC=90°，‎ ‎∴△CFG为等腰直角三角形，‎ ‎∴GF=FC，‎ ‎∵EG=EF﹣GF，DF=CD﹣FC，‎ ‎∴EG=DF，故①正确；‎ ‎②∵△CFG为等腰直角三角形，H为CG的中点，‎ ‎∴FH=CH，∠GFH=∠GFC=45°=∠HCD，‎ 在△EHF和△DHC中，，‎ ‎∴△EHF≌△DHC（SAS），‎ ‎∴∠HEF=∠HDC，‎ ‎∴∠AEH+∠ADH=∠AEF+∠HEF+∠ADF﹣∠HDC=∠AEF+∠ADF=180°，故②正确；‎ ‎③∵△CFG为等腰直角三角形，H为CG的中点，‎ ‎∴FH=CH，∠GFH=∠GFC=45°=∠HCD，‎ 在△EHF和△DHC中，，‎ ‎∴△EHF≌△DHC（SAS），故③正确；‎ ‎④∵=，‎ ‎∴AE=2BE，‎ ‎∵△CFG为等腰直角三角形，H为CG的中点，‎ ‎∴FH=GH，∠FHG=90°，‎ ‎∵∠EGH=∠FHG+∠HFG=90°+∠HFG=∠HFD，‎ 在△EGH和△DFH中，，‎ ‎∴△EGH≌△DFH（SAS），‎ ‎∴∠EHG=∠DHF，EH=DH，∠DHE=∠EHG+∠DHG=∠DHF+∠DHG=∠FHG=90°，‎ ‎∴△EHD为等腰直角三角形，‎ 过H点作HM垂直于CD于M点，如图所示：‎ 设HM=x，则DM=5x，DH=x，CD=6x，‎ 则S△DHC=×HM×CD=3x2，S△EDH=×DH2=13x2，‎ ‎∴3S△EDH=13S△DHC，故④正确；‎ 故选：D．‎ ‎7. （2016·四川攀枝花）如图，二次函数y=ax2+bx+c（a＞0）图象的顶点为D，其图象与x轴的交点A、B的横坐标分别为﹣1和3，则下列结论正确的是（　　）‎ A．‎2a﹣b=0‎ B．a+b+c＞0‎ C．‎3a﹣c=0‎ D．当a=时，△ABD是等腰直角三角形 ‎【考点】二次函数图象与系数的关系．‎ ‎【分析】由于抛物线与x轴的交点A、B的横坐标分别为﹣1，3，得到对称轴为直线x=1，则﹣=1，即‎2a+b=0，得出，选项A错误；‎ 当x=1时，y＜0，得出a+b+c＜0，得出选项B错误；‎ 当x=﹣1时，y=0，即a﹣b+c=0，而b=﹣‎2a，可得到a与c的关系，得出选项C错误；‎ 由a=，则b=﹣1，c=﹣，对称轴x=1与x轴的交点为E，先求出顶点D的坐标，由三角形边的关系得出△ADE和△BDE都为等腰直角三角形，得出选项D正确；即可得出结论．‎ ‎【解答】解：∵抛物线与x轴的交点A、B的横坐标分别为﹣1，3，‎ ‎∴抛物线的对称轴为直线x=1，则﹣=1，‎ ‎∴‎2a+b=0，‎ ‎∴选项A错误；‎ ‎∴当自变量取1时，对应的函数图象在x轴下方，‎ ‎∴x=1时，y＜0，则a+b+c＜0，‎ ‎∴选项B错误；‎ ‎∵A点坐标为（﹣1，0），‎ ‎∴a﹣b+c=0，而b=﹣‎2a，‎ ‎∴a+‎2a+c=0，‎ ‎∴‎3a+c=0，‎ ‎∴选项C错误；‎ 当a=，则b=﹣1，c=﹣，对称轴x=1与x轴的交点为E，如图，‎ ‎∴抛物线的解析式为y=x2﹣x﹣，‎ 把x=1代入得y=﹣1﹣=﹣2，‎ ‎∴D点坐标为（1，﹣2），‎ ‎∴AE=2，BE=2，DE=2，‎ ‎∴△ADE和△BDE都为等腰直角三角形，‎ ‎∴△ADB为等腰直角三角形，‎ ‎∴选项D正确．‎ 故选D．‎ ‎【点评】本题考查了二次函数y=ax2+bx+c的图象与系数的关系：当a＞0，抛物线开口向上；抛物线的对称轴为直线x=﹣；抛物线与y轴的交点坐标为（0，c）．‎ ‎8. （2016·四川眉山·3分）如图，已知点A是双曲线在第三象限分支上的一个动点，连结AO并延长交另一分支于点B，以AB为边作等边三角形ABC，点C在第四象限内，且随着点A的运动，点C的位置也在不断变化，但点C始终在双曲线上运动，则k的值是　﹣3　．‎ ‎【分析】根据反比例函数的性质得出OA=OB，连接OC，过点A作AE⊥y轴，垂足为E，过点C作CF⊥y轴，垂足为F，根据等边三角形的性质和解直角三角形求出OC=OA，求出△OFC∽△AEO，相似比，求出面积比，求出△OFC的面积，即可得出答案．‎ ‎【解答】解：∵双曲线的图象关于原点对称，‎ ‎∴点A与点B关于原点对称，‎ ‎∴OA=OB，‎ 连接OC，如图所示，‎ ‎∵△ABC是等边三角形，OA=OB，‎ ‎∴OC⊥AB．∠BAC=60°，‎ ‎∴tan∠OAC==，‎ ‎∴OC=OA，‎ 过点A作AE⊥y轴，垂足为E，过点C作CF⊥y轴，垂足为F，‎ ‎∵AE⊥OE，CF⊥OF，OC⊥OA，‎ ‎∴∠AEO=∠OFC，∠AOE=90°﹣∠FOC=∠OCF，‎ ‎∴△OFC∽△AEO，相似比，‎ ‎∴面积比，‎ ‎∵点A在第一象限，设点A坐标为（a，b），‎ ‎∵点A在双曲线上，‎ ‎∴S△AEO=ab=，‎ ‎∴S△OFC=FC•OF=，‎ ‎∴设点C坐标为（x，y），‎ ‎∵点C在双曲线上，‎ ‎∴k=xy，‎ ‎∵点C在第四象限，‎ ‎∴FC=x，OF=﹣y．‎ ‎∴FC•OF=x•（﹣y）=﹣xy=﹣，‎ 故答案为：﹣3．‎ ‎【点评】本题考查了反比例函数图象上点的坐标特征，等边三角形的性质，解直角三角形，相似三角形的性质和判定的应用，能综合运用知识点进行 推理和计算是解此题的关键．‎