深圳中考数学试卷及试卷分析

深圳中考数学试卷及试卷分析

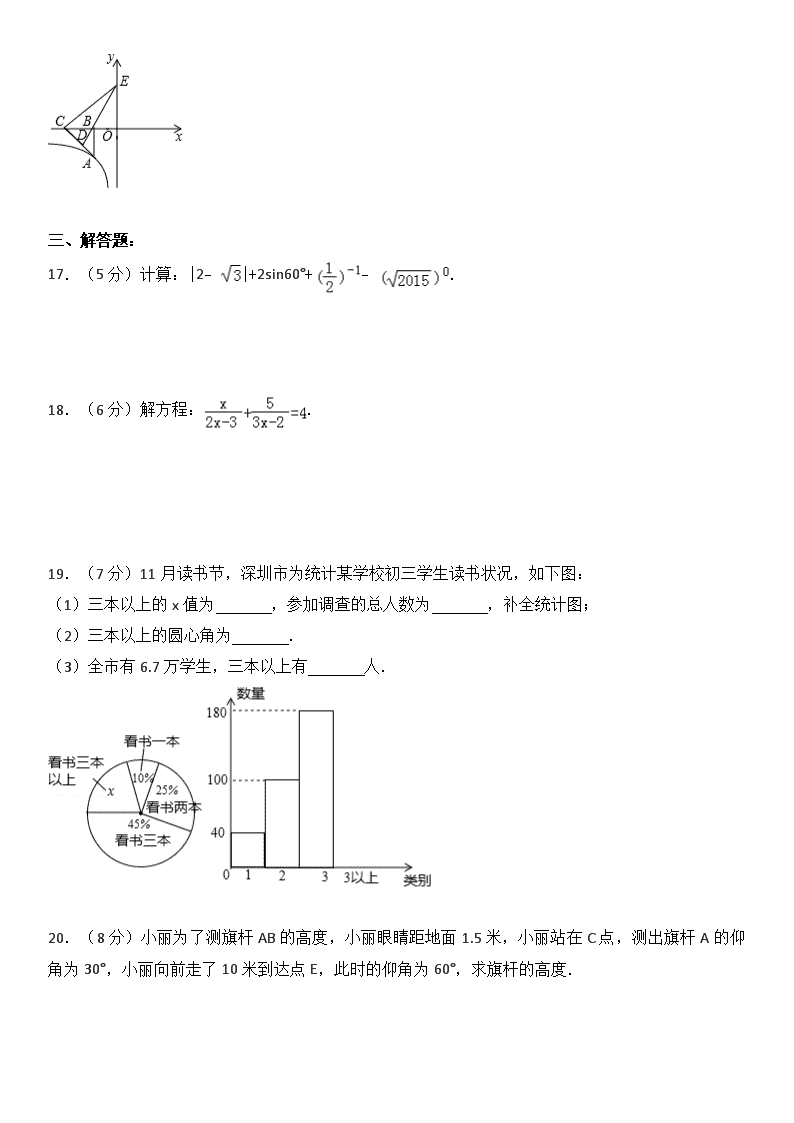
‎2015年广东省深圳市中考数学试卷 ‎　一、选择题：‎ ‎1．（3分）﹣15的相反数是（　　）‎ A．15 B．﹣15 C． D．‎ ‎2．（3分）用科学记数法表示316000000为（　　）‎ A．3.16×107 B．3.16×108 C．31.6×107 D．31.6×106‎ ‎3．（3分）下列说法错误的是（　　）‎ A．a•a=a2 B．2a+a=3a C．（a3）2=a5 D．a3÷a﹣1=a4‎ ‎4．（3分）下列图形既是中心对称又是轴对称图形的是（　　）‎ A． B． C． D．‎ ‎5．（3分）下列主视图正确的是（　　）‎ A． B． C． D．‎ ‎6．（3分）在以下数据75，80，80，85，90中，众数、中位数分别是（　　）‎ A．75，80 B．80，80 C．80，85 D．80，90‎ ‎7．（3分）解不等式2x≥x﹣1，并把解集在数轴上表示（　　）‎ A． B． C． D．‎ ‎8．（3分）二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列说法正确的个数是（　　）‎ ‎①a＞0；②b＞0；③c＜0；④b2﹣4ac＞0．‎ A．1 B．2 C．3 D．4‎ ‎9．（3分）如图，AB为⊙O直径，已知∠DCB=20°，则∠DBA为（　　）‎ A．50° B．20° C．60° D．70°‎ ‎10．（3分）某商品的标价为200元，8折销售仍赚40元，则商品进价为（　　）元．‎ A．140 B．120 C．160 D．100‎ ‎11．（3分）如图，已知△ABC，AB＜BC，用尺规作图的方法在BC上取一点P，使得PA+PC=BC，则下列选项正确的是（　　）‎ A． B． C． D．‎ ‎12．（3分）如图，已知正方形ABCD的边长为12，BE=EC，将正方形边CD沿DE折叠到DF，延长EF交AB于G，连接DG，现在有如下4个结论：①△ADG≌△FDG；②GB=2AG；③△GDE∽△BEF；④S△BEF=．在以上4个结论中，正确的有（　　）‎ A．1 B．2 C．3 D．4‎ ‎　‎ 二、填空题：‎ ‎13．（3分）因式分解：3a2﹣3b2=　 　．‎ ‎14．（3分）在数字1，2，3中任选两个组成一个两位数，则这个两位数能被3整除的概率是　 　．‎ ‎15．（3分）观察下列图形，它们是按一定规律排列的，依照此规律，第5个图形有　 　个太阳．‎ ‎16．（3分）如图，已知点A在反比例函数y=（x＜0）上，作Rt△ABC，点D为斜边AC的中点，连DB并延长交y轴于点E．若△BCE的面积为8，则k=　 　．‎ ‎　‎ 三、解答题：‎ ‎17．（5分）计算：|2﹣|+2sin60°+﹣．‎ ‎18．（6分）解方程：．‎ ‎19．（7分）11月读书节，深圳市为统计某学校初三学生读书状况，如下图：‎ ‎（1）三本以上的x值为　 　，参加调查的总人数为　 　，补全统计图；‎ ‎（2）三本以上的圆心角为　 　．‎ ‎（3）全市有6.7万学生，三本以上有　 　人．‎ ‎20．（8分）小丽为了测旗杆AB的高度，小丽眼睛距地面1.5米，小丽站在C点，测出旗杆A的仰角为30°，小丽向前走了10米到达点E，此时的仰角为60°，求旗杆的高度．‎ ‎21．（8分）下表为深圳市居民每月用水收费标准，（单位：元/m3）．‎ 用水量 单价 x≤22‎ a 剩余部分 a+1.1‎ ‎（1）某用户用水10立方米，共交水费23元，求a的值；‎ ‎（2）在（1）的前提下，该用户5月份交水费71元，请问该用户用水多少立方米？‎ ‎22．（9分）如图1，水平放置一个直角三角板和一个量角器，三角板的边AB和量角器的直径DE在一条直线上，AB=BC=6cm，OD=3cm，开始的时候BD=1cm，现在三角板以2cm/s的速度向右移动．‎ ‎（1）当B与O重合的时候，求三角板运动的时间；‎ ‎（2）如图2，当AC与半圆相切时，求AD；‎ ‎（3）如图3，当AB和DE重合时，求证：CF2=CG•CE．‎ ‎23．（9分）如图1，关于x的二次函数y=﹣x2+bx+c经过点A（﹣3，0），点C（0，3），点D为二次函数的顶点，DE为二次函数的对称轴，E在x轴上．‎ ‎（1）求抛物线的解析式；‎ ‎（2）DE上是否存在点P到AD的距离与到x轴的距离相等？若存在求出点P，若不存在请说明理由；‎ ‎（3）如图2，DE的左侧抛物线上是否存在点F，使2S△FBC=3S△EBC？若存在求出点F的坐标，若不存在请说明理由．‎ ‎　‎ ‎2015年广东省深圳市中考数学试卷 参考答案与试题解析 ‎　‎ 一、选择题：‎ ‎1．（3分）﹣15的相反数是（　　）‎ A．15 B．﹣15 C． D．‎ ‎【分析】根据只有符号不同的两个数互为相反数，可得一个数的相反数．‎ ‎【解答】解：﹣15的相反数是15，‎ 故选：A．‎ ‎【点评】本题考查了相反数，在一个数的前面加上负号就是这个数的相反数．‎ ‎　‎ ‎2．（3分）用科学记数法表示316000000为（　　）‎ A．3.16×107 B．3.16×108 C．31.6×107 D．31.6×106‎ ‎【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．‎ ‎【解答】解：将316000000用科学记数法表示为：3.16×108．‎ 故选：B．‎ ‎【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．‎ ‎　‎ ‎3．（3分）下列说法错误的是（　　）‎ A．a•a=a2 B．2a+a=3a C．（a3）2=a5 D．a3÷a﹣1=a4‎ ‎【分析】根据同底数幂相乘，底数不变指数相加；同底数幂相除，底数不变指数相减；幂的乘方，底数不变指数相乘；合并同类项法则对各选项分析判断即可得解．‎ ‎【解答】解：A、a•a=a2，正确，故本选项错误；‎ B、2a+a=3a，正确，故本选项错误；‎ C、（a3）2=a3×2=a6，故本选项正确；‎ D、a3÷a﹣1=a3﹣（﹣1）=a4，正确，故本选项错误．‎ 故选：C．‎ ‎【点评】本题考查了合并同类项，同底数幂的乘法，幂的乘方的性质，同底数幂的除法，熟练掌握运算性质和法则是解题的关键．‎ ‎　‎ ‎4．（3分）下列图形既是中心对称又是轴对称图形的是（　　）‎ A． B． C． D．‎ ‎【分析】根据中心对称图形的定义旋转180°后能够与原图形完全重合即是中心对称图形，以及轴对称图形的定义即可判断出．‎ ‎【解答】解：A、∵此图形旋转180°后不能与原图形重合，∴此图形不是中心对称图形，是轴对称图形，故此选项错误．‎ B、∵此图形旋转180°后不能与原图形重合，∴此图形不是中心对称图形，是轴对称图形，故此选项错误；‎ C、此图形旋转180°后不能与原图形重合，此图形不是中心对称图形，是轴对称图形，故此选项错误；‎ D、∵此图形旋转180°后能与原图形重合，∴此图形是中心对称图形，也是轴对称图形，故此选项正确．‎ 故选：D．‎ ‎【点评】此题主要考查了中心对称图形与轴对称的定义，根据定义得出图形形状是解决问题的关键．‎ ‎　‎ ‎5．（3分）下列主视图正确的是（　　）‎ A． B． C． D．‎ ‎【分析】根据从正面看得到的图形是主视图，可得答案．‎ ‎【解答】解：从正面看第一层是三个小正方形，第二层中间一个小正方形．‎ 故选：A．‎ ‎【点评】本题考查了简单组合体的三视图，从正面看得到的视图是主视图．‎ ‎　‎ ‎6．（3分）在以下数据75，80，80，85，90中，众数、中位数分别是（　　）‎ A．75，80 B．80，80 C．80，85 D．80，90‎ ‎【分析】首先找出这组数据中出现次数最多的数，则它就是这组数据的众数；然后把这组数据从小到大排列，则中间的数就是这组数据的中位数，据此解答即可．‎ ‎【解答】解：∵数据75，80，80，85，90中，80出现的次数最多，出现了2次，‎ ‎∴这组数据的众数是80；‎ 把数据75，80，80，85，90从小到大排列，可得 ‎75，80，80，85，90，‎ 所以这组数据的中位数是80．‎ 故选：B．‎ ‎【点评】（1）此题主要考查了众数的含义和求法，要熟练掌握，解答此题的关键是要明确：①一组数据中出现次数最多的数据叫做众数．②求一组数据的众数的方法：找出频数最多的那个数据，若几个数据频数都是最多且相同，此时众数就是这多个数据．‎ ‎（2）此题还考查了中位数的含义和求法，要熟练掌握，解答此题的关键是要明确：将一组数据按照从小到大（或从大到小）的顺序排列，①如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数．②如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数．‎ ‎　‎ ‎7．（3分）解不等式2x≥x﹣1，并把解集在数轴上表示（　　）‎ A． B． C． D．‎ ‎【分析】先移项、合并同类项，把x的系数化为1即可．‎ ‎【解答】解：2x≥x﹣1，‎ ‎2x﹣x≥﹣1，‎ x≥﹣1．‎ 故选：B．‎ ‎【点评】本题考查了解一元一次不等式、在数轴上表示不等式的解集．把不等式的解集在数轴上表示出来（＞，≥向右画；＜，≤向左画）．在表示解集时“≥”，“≤”要用实心圆点表示；“＜”，“＞”要用空心圆点表示．‎ ‎　‎ ‎8．（3分）二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列说法正确的个数是（　　）‎ ‎①a＞0；②b＞0；③c＜0；④b2﹣4ac＞0．‎ A．1 B．2 C．3 D．4‎ ‎【分析】根据抛物线开口方向对①进行判断；根据抛物线的对称轴位置对②进行判断；根据抛物线与y轴的交点位置对③进行判断；根据抛物线与x轴的交点个数对④进行判断．‎ ‎【解答】解：∵抛物线开口向下，‎ ‎∴a＜0，所以①错误；‎ ‎∵抛物线的对称轴在y轴右侧，‎ ‎∴﹣＞0，‎ ‎∴b＞0，所以②正确；‎ ‎∵抛物线与y轴的交点在x轴上方，‎ ‎∴c＞0，所以③错误；‎ ‎∵抛物线与x轴有2个交点，‎ ‎∴△=b2﹣4ac＞0，所以④正确．‎ 故选：B．‎ ‎【点评】本题考查了二次函数图象与系数的关系：对于二次函数y=ax2+bx+c（a≠0），二次项系数a决定抛物线的开口方向和大小，当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口；一次项系数b和二次项系数a共同决定对称轴的位置：当a与b同号时（即ab＞0），对称轴在y轴左； 当a与b异号时（即ab＜0），对称轴在y轴右．（简称：左同右异）；常数项c决定抛物线与y轴交点：抛物线与y轴交于（0，c）．抛物线与x轴交点个数由△决定：△=b2﹣4ac＞0时，抛物线与x轴有2个交点；△=b2﹣4ac=0时，抛物线与x轴有1个交点；△=b2﹣4ac＜0时，抛物线与x轴没有交点．‎ ‎　‎ ‎9．（3分）如图，AB为⊙O直径，已知∠DCB=20°，则∠DBA为（　　）‎ A．50° B．20° C．60° D．70°‎ ‎【分析】先根据半圆（或直径）所对的圆周角是直角得到∠ACB=90°，再利用互余得∠ACD=90°﹣∠DCB=70°，然后根据同弧或等弧所对的圆周角相等求解．‎ ‎【解答】解：∵AB为⊙O直径，‎ ‎∴∠ACB=90°，‎ ‎∴∠ACD=90°﹣∠DCB=90°﹣20°=70°，‎ ‎∴∠DBA=∠ACD=70°．‎ 故选：D．‎ ‎【点评】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．‎ ‎　‎ ‎10．（3分）某商品的标价为200元，8折销售仍赚40元，则商品进价为（　　）元．‎ A．140 B．120 C．160 D．100‎ ‎【分析】设商品进价为每件x元，则售价为每件0.8×200元，由利润=售价﹣进价建立方程求出其解即可．‎ ‎【解答】解：设商品的进价为每件x元，售价为每件0.8×200元，由题意，得 ‎0.8×200=x+40，‎ 解得：x=120．‎ 故选：B．‎ ‎【点评】本题考查了销售问题的数量关系利润=售价﹣进价的运用，列一元一次方程解实际问题的运用，解答时根据销售问题的数量关系建立方程是关键．‎ ‎　‎ ‎11．（3分）如图，已知△ABC，AB＜BC，用尺规作图的方法在BC上取一点P，使得PA+PC=BC，则下列选项正确的是（　　）‎ A． B． C． D．‎ ‎【分析】由PB+PC=BC和PA+PC=BC易得PA=PB，根据线段垂直平分线定理的逆定理可得点P在AB的垂直平分线上，于是可判断D选项正确．‎ ‎【解答】解：∵PB+PC=BC，‎ 而PA+PC=BC，‎ ‎∴PA=PB，‎ ‎∴点P在AB的垂直平分线上，‎ 即点P为AB的垂直平分线与BC的交点．‎ 故选：D．‎ ‎【点评】本题考查了复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．‎ ‎　‎ ‎12．（3分）如图，已知正方形ABCD的边长为12，BE=EC，将正方形边CD沿DE折叠到DF，延长EF交AB于G，连接DG，现在有如下4个结论：①△ADG≌△FDG；②GB=2AG；③△GDE∽△BEF；④S△BEF=．在以上4个结论中，正确的有（　　）‎ A．1 B．2 C．3 D．4‎ ‎【分析】根据正方形的性质和折叠的性质可得AD=DF，∠A=∠GFD=90°，于是根据“HL”判定△ADG≌△FDG，再由GF+GB=GA+GB=12，EB=EF，△BGE为直角三角形，可通过勾股定理列方程求出AG=4，BG=8，进而求出△BEF的面积，再抓住△BEF是等腰三角形，而△GED显然不是等腰三角形，判断③是错误的．‎ ‎【解答】解：由折叠可知，DF=DC=DA，∠DFE=∠C=90°，‎ ‎∴∠DFG=∠A=90°，‎ ‎∴△ADG≌△FDG，①正确；‎ ‎∵正方形边长是12，‎ ‎∴BE=EC=EF=6，‎ 设AG=FG=x，则EG=x+6，BG=12﹣x，‎ 由勾股定理得：EG2=BE2+BG2，‎ 即：（x+6）2=62+（12﹣x）2，‎ 解得：x=4‎ ‎∴AG=GF=4，BG=8，BG=2AG，②正确；‎ BE=EF=6，△BEF是等腰三角形，易知△GED不是等腰三角形，③错误；‎ S△GBE=×6×8=24，S△BEF=•S△GBE==，④正确．‎ 故选：C．‎ ‎【点评】本题综合性较强，考查了翻折变换的性质和正方形的性质，全等三角形的判定与性质，勾股定理，平行线的判定，三角形的面积计算，有一定的难度．‎ ‎　‎ 二、填空题：‎ ‎13．（3分）因式分解：3a2﹣3b2=　3（a+b）（a﹣b）　．‎ ‎【分析】原式提取3，再利用平方差公式分解即可．‎ ‎【解答】解：原式=3（a2﹣b2）=3（a+b）（a﹣b），‎ 故答案为：3（a+b）（a﹣b）‎ ‎【点评】此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．‎ ‎　‎ ‎14．（3分）在数字1，2，3中任选两个组成一个两位数，则这个两位数能被3整除的概率是　　．‎ ‎【分析】利用树状图法列举出所有可能，看是否能被3整除．找出满足条件的数的个数除以总的个数即可．‎ ‎【解答】解：如图所示：‎ 共有6种情况，能被3整除的有12，21两种．因此概率为=．‎ 故答案为：．‎ ‎【点评】本题考查了树状图法求概率以及概率公式，注意能被3整除即两位数加起来和为3的倍数．‎ ‎　‎ ‎15．（3分）观察下列图形，它们是按一定规律排列的，依照此规律，第5个图形有　21　个太阳．‎ ‎【分析】‎ 由图形可以看出：第一行小太阳的个数是从1开始连续的自然数，第二行小太阳的个数是1、2、4、8、…、2n﹣1，由此计算得出答案即可．‎ ‎【解答】解：第一行小太阳的个数为1、2、3、4、…，第5个图形有5个太阳，‎ 第二行小太阳的个数是1、2、4、8、…、2n﹣1，第5个图形有24=16个太阳，‎ 所以第5个图形共有5+16=21个太阳．‎ 故答案为：21．‎ ‎【点评】此题考查图形的变化规律，找出图形之间的运算规律，利用规律解决问题．‎ ‎　‎ ‎16．（3分）如图，已知点A在反比例函数y=（x＜0）上，作Rt△ABC，点D为斜边AC的中点，连DB并延长交y轴于点E．若△BCE的面积为8，则k=　16　．‎ ‎【分析】根据反比例函数系数k的几何意义，证明△ABC∽△EOB，根据相似比求出BA•BO的值，从而求出△AOB的面积．‎ ‎【解答】解：∵△BCE的面积为8，‎ ‎∴，‎ ‎∴BC•OE=16，‎ ‎∵点D为斜边AC的中点，‎ ‎∴BD=DC，‎ ‎∴∠DBC=∠DCB=∠EBO，‎ 又∠EOB=∠ABC，‎ ‎∴△EOB∽△ABC，‎ ‎∴，‎ ‎∴AB•OB•=BC•OE ‎∴k=AB•BO=BC•OE=16．‎ 故答案为：16．‎ ‎【点评】本题考查了反比例函数系数k的几何意义，解决本题的关键是证明△EOB∽△ABC，得到AB•OB•=BC•OE．‎ ‎　‎ 三、解答题：‎ ‎17．（5分）计算：|2﹣|+2sin60°+﹣．‎ ‎【分析】原式第一项利用绝对值的代数意义化简，第二项利用特殊角的三角函数值计算，第三项利用负整数指数幂法则计算，最后一项利用零指数幂法则计算即可得到结果．‎ ‎【解答】解：原式=2﹣+2×+2﹣1=3．‎ ‎【点评】此题考查了实数的运算，熟练掌握运算法则是解本题的关键．‎ ‎　‎ ‎18．（6分）解方程：．‎ ‎【分析】分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．‎ ‎【解答】解：去分母得：3x2﹣2x+10x﹣15=4（2x﹣3）（3x﹣2），‎ 整理得：3x2﹣2x+10x﹣15=24x2﹣52x+24，即7x2﹣20x+13=0，‎ 分解因式得：（x﹣1）（7x﹣13）=0，‎ 解得：x1=1，x2=，‎ 经检验x1=1与x2=都为分式方程的解．‎ ‎【点评】此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．‎ ‎　‎ ‎19．（7分）11月读书节，深圳市为统计某学校初三学生读书状况，如下图：‎ ‎（1）三本以上的x值为　20%　，参加调查的总人数为　400　，补全统计图；‎ ‎（2）三本以上的圆心角为　72°　．‎ ‎（3）全市有6.7万学生，三本以上有　13400　人．‎ ‎【分析】（1）根据看1本书的人数为40人，所占的百分比为10%，40÷‎ ‎10即可求出总人数，用100%﹣10%﹣25%﹣45%即可得x的值，用总人数乘以x的值，即可得到3本以上的人数，即可补全统计图；‎ ‎（2）用x的值乘以360°，即可得到圆心角；‎ ‎（3）用6.7万乘以三本以上的百分比，即可解答．‎ ‎【解答】解：（1）40÷10%=400（人），‎ x=100%﹣10%﹣25%﹣45%=20%，400×20%=80（人），‎ 故答案为：20%，400；‎ 如图所示；‎ ‎（2）20%×360°=72°，‎ 故答案为：72°；‎ ‎（3）67000×20%=13400（人），‎ 故答案为：13400．‎ ‎【点评】此题主要考查了条形图与扇形图的综合应用，解决此类问题注意图形有机结合，综合分析获取正确信息．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．‎ ‎　‎ ‎20．（8分）小丽为了测旗杆AB的高度，小丽眼睛距地面1.5米，小丽站在C点，测出旗杆A的仰角为30°，小丽向前走了10米到达点E，此时的仰角为60°，求旗杆的高度．‎ ‎【分析】关键三角形外角的性质求得∠DAF=30°，得出AF=DF=10，在Rt△FGA中，根据正弦函数求出AG的长，加上BG的长即为旗杆高度．‎ ‎【解答】解：如图，∵∠ADG=30°，∠AFG=60°，‎ ‎∴∠DAF=30°，‎ ‎∴AF=DF=10，‎ 在Rt△FGA中，‎ AG=AF•sin∠AFG=10×=5，‎ ‎∴AB=1.5+5．‎ 答：旗杆AB的高度为（1.5+5）米．‎ ‎【点评】本题考查了解直角三角形的应用﹣﹣仰角俯角问题，要求学生能借助仰角构造直角三角形并解直角三角形．‎ ‎　‎ ‎21．（8分）下表为深圳市居民每月用水收费标准，（单位：元/m3）．‎ 用水量 单价 x≤22‎ a 剩余部分 a+1.1‎ ‎（1）某用户用水10立方米，共交水费23元，求a的值；‎ ‎（2）在（1）的前提下，该用户5月份交水费71元，请问该用户用水多少立方米？‎ ‎【分析】（1）直接利用10a=23进而求出即可；‎ ‎（2）首先判断得出x＞22，进而表示出总水费进而得出即可．‎ ‎【解答】解：（1）由题意可得：10a=23，‎ 解得：a=2.3，‎ 答：a的值为2.3；‎ ‎（2）设用户水量为x立方米，‎ ‎∵用水22立方米时，水费为：22×2.3=50.6＜71，‎ ‎∴x＞22，‎ ‎∴22×2.3+（x﹣22）×（2.3+1.1）=71，‎ 解得：x=28，‎ 答：该用户用水28立方米．‎ ‎【点评】此题主要考查了一元一次方程的应用，根据图表中数据得出用户用水为x米3（x＞22）时的水费是解题关键．‎ ‎　‎ ‎22．（9分）如图1，水平放置一个直角三角板和一个量角器，三角板的边AB和量角器的直径DE在一条直线上，AB=BC=6cm，OD=3cm，开始的时候BD=1cm，现在三角板以2cm/s的速度向右移动．‎ ‎（1）当B与O重合的时候，求三角板运动的时间；‎ ‎（2）如图2，当AC与半圆相切时，求AD；‎ ‎（3）如图3，当AB和DE重合时，求证：CF2=CG•CE．‎ ‎【分析】（1）根据题意得出BO的长，再利用路程除以速度得出时间；‎ ‎（2）根据切线的性质和判定结合等腰直角三角形的性质得出AO的长，进而求出答案；‎ ‎（3）利用圆周角定理以及切线的性质定理得出∠CEF=∠ODF=∠OFD=∠CFG，进而求出△CFG∽△CEF，即可得出答案．‎ ‎【解答】（1）解：由题意可得：BO=4cm，t==2（s）；‎ ‎（2）解：如图2，连接O与切点H，则OH⊥AC，‎ 又∵∠A=45°，‎ ‎∴AO=OH=3cm，‎ ‎∴AD=AO﹣DO=（3﹣3）cm；‎ ‎（3）证明：如图3，连接EF，‎ ‎∵OD=OF，‎ ‎∴∠ODF=∠OFD，‎ ‎∵DE为直径，‎ ‎∴∠ODF+∠DEF=90°，‎ ‎∠DEC=∠DEF+∠CEF=90°，‎ ‎∴∠CEF=∠ODF=∠OFD=∠CFG，‎ 又∵∠FCG=∠ECF，‎ ‎∴△CFG∽△CEF，‎ ‎∴=，‎ ‎∴CF2=CG•CE．‎ ‎【点评】此题主要考查了切线的性质以及相似三角形的判定与性质、等腰直角三角形的性质等知识，根据题意得出△CFG∽△CEF是解题关键．‎ ‎　‎ ‎23．（9分）如图1，关于x的二次函数y=﹣x2+bx+c经过点A（﹣3，0），点C（0，3），点D为二次函数的顶点，DE为二次函数的对称轴，E在x轴上．‎ ‎（1）求抛物线的解析式；‎ ‎（2）DE上是否存在点P到AD的距离与到x轴的距离相等？若存在求出点P，若不存在请说明理由；‎ ‎（3）如图2，DE的左侧抛物线上是否存在点F，使2S△FBC=3S△EBC？若存在求出点F的坐标，若不存在请说明理由．‎ ‎【分析】（1）把A、C两点坐标代入可求得b、c，可求得抛物线解析式；‎ ‎（2）当点P在∠DAB的平分线上时，过P作PM⊥AD，设出P点坐标，可表示出PM、PE，由角平分线的性质可得到PM=PE，可求得P点坐标；当点P在∠DAB外角平分线上时，同理可求得P点坐标；‎ ‎（3）可先求得△FBC的面积，过F作FQ⊥x轴，交BC的延长线于Q，可求得FQ的长，可设出F点坐标，表示出B点坐标，从而可表示出FQ的长，可求得F点坐标．‎ ‎【解答】解：‎ ‎（1）∵二次函数y=﹣x2+bx+c经过点A（﹣3，0），点C（0，3），‎ ‎∴，解得，‎ ‎∴抛物线的解析式y=﹣x2﹣2x+3，‎ ‎（2）存在，‎ 当P在∠DAB的平分线上时，如图1，作PM⊥AD，‎ 设P（﹣1，m），则PM=PD•sin∠ADE=（4﹣m），PE=m，‎ ‎∵PM=PE，‎ ‎∴（4﹣m）=m，m=﹣1，‎ ‎∴P点坐标为（﹣1，﹣1）；‎ 当P在∠DAB的外角平分线上时，如图2，作PN⊥AD，‎ 设P（﹣1，n），则PN=PD•sin∠ADE=（4﹣n），PE=﹣n，‎ ‎∵PN=PE，‎ ‎∴（4﹣n）=﹣n，n=﹣﹣1，‎ ‎∴P点坐标为（﹣1，﹣﹣1）；‎ 综上可知存在满足条件的P点，其坐标为（﹣1，﹣1）或（﹣1，﹣﹣1）；‎ ‎（3）∵抛物线的解析式y=﹣x2﹣2x+3，‎ ‎∴B（1，0），‎ ‎∴S△EBC=EB•OC=3，‎ ‎∵2S△FBC=3S△EBC，‎ ‎∴S△FBC=，‎ 过F作FQ⊥x轴于点H，交BC的延长线于Q，过F作FM⊥y轴于点M，如图3，‎ ‎∵S△FBC=S△BQH﹣S△BFH﹣S△CFQ=HB•HQ﹣BH•HF﹣QF•FM=BH（HQ﹣HF）﹣QF•FM=BH•QF﹣QF•FM=QF•（BH﹣FM）=FQ•OB=FQ=，‎ ‎∴FQ=9，‎ ‎∵BC的解析式为y=﹣3x+3，‎ 设F（x0，﹣x02﹣2x0+3），‎ ‎∴﹣3x0+3+x02+2x0﹣3=9，‎ 解得：x0=或（舍去），‎ ‎∴点F的坐标是（，），‎ ‎∵S△ABC=6＞，‎ ‎∴点F不可能在A点下方，‎ 综上可知F点的坐标为（，）．‎ ‎【点评】本题主要考查二次函数的综合应用，涉及待定系数法、角平分线的性质、三角函数、三角形面积等知识点．在（1）中注意待定系数法的应用步骤，在（2）中注意分点P在∠DAB的角平分线上和在外角的平分线上两种情况，在（3）中求得FQ的长是解题的关键．本题所考查知识点较多，综合性很强，难度适中．‎ ‎　‎