2010中考数学试题分类汇编共28专题28动态几何

2010中考数学试题分类汇编共28专题28动态几何

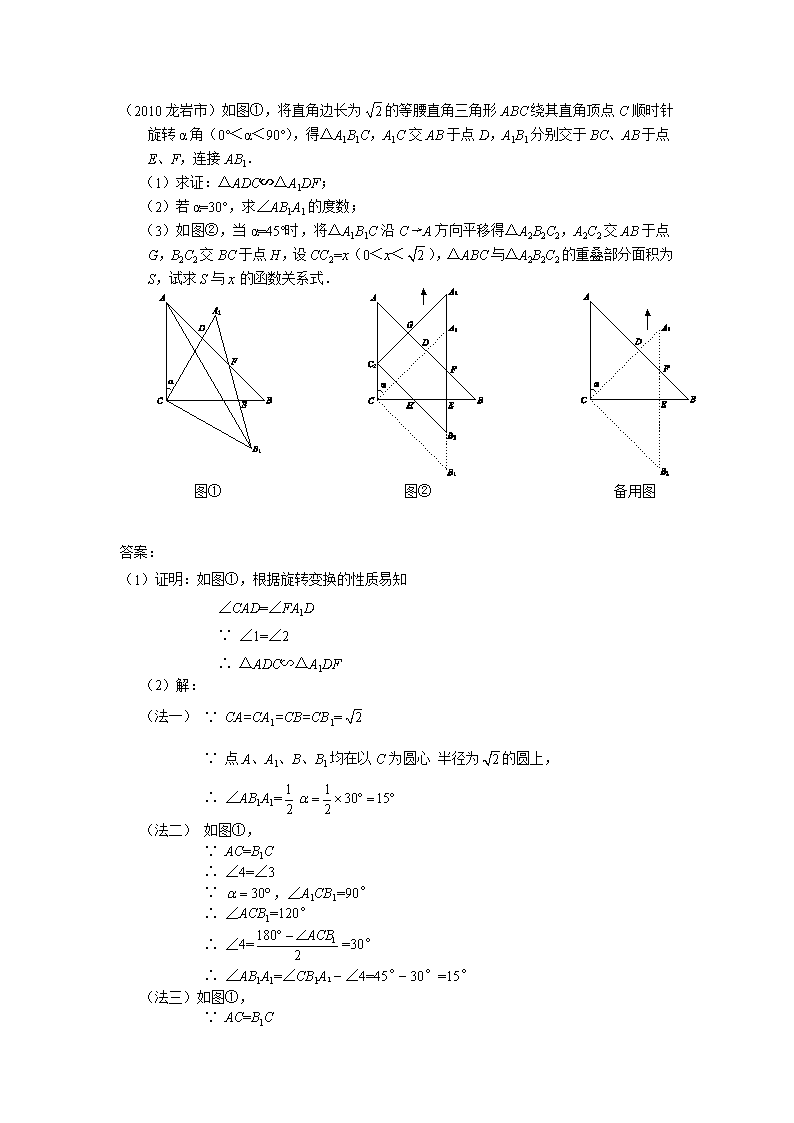
‎（2010龙岩市）如图①，将直角边长为的等腰直角三角形ABC绕其直角顶点C顺时针旋转α角（0°＜α＜90°），得△A1B‎1C，A‎1C交AB于点D，A1B1分别交于BC、AB于点E、F，连接AB1．‎ ‎（1）求证：△ADC∽△A1DF；‎ ‎（2）若α=30°，求∠AB‎1A1的度数；‎ ‎（3）如图②，当α=45°时，将△A1B‎1C沿C→A方向平移得△A2B‎2C2，A‎2C2交AB于点G，B‎2C2交BC于点H，设CC2=x（0＜x＜），△ABC与△A2B‎2C2的重叠部分面积为S，试求S与x的函数关系式．‎ 图①　　 图② 备用图 答案：‎ ‎（1）证明：如图①，根据旋转变换的性质易知 ‎ ∠CAD=∠FA1D ‎ ‎ ∵ ∠1=∠2 ‎ ‎ ∴ △ADC∽△A1DF ‎ ‎ （2）解：‎ ‎（法一） ∵ CA=CA1=CB=CB1=‎ ‎∵ 点A、A1、B、B1均在以C为圆心 半径为的圆上， ‎ ‎∴ ∠AB‎1A1= ‎ ‎ （法二） 如图①，‎ ‎∵ AC=B‎1C ‎ ∴ ∠4=∠3 ‎ ‎ ∵ ，∠A1CB1=90°‎ ‎ ∴ ∠ACB1=120° ‎ ‎ ∴ ∠4==30° ‎ ‎ ∴ ∠AB‎1A1=∠CB‎1A1∠4=45°30°=15° ‎ ‎ （法三）如图①，‎ ‎∵ AC=B‎1C ‎ ∴ ∠4=∠3 ‎ ‎ ∵ ∠CAB=∠CB‎1A1 ‎ ‎∴ ∠CAB∠3=∠CB‎1A1∠4‎ 即 ∠B1AB=∠AB‎1A1 ‎ ‎∵ ∠5=∠B1AB+∠AB‎1A1‎ ‎∴ ∠5=2∠AB‎1A1 ‎ ‎∵ △ADC∽△A1DF ‎ ‎∴ ∠5= ‎ ‎∴ ∠AB‎1A1= ‎ ‎ （3）解：△A1B‎1C在平移的过程中，易证得△AC‎2G、△HB2E、△A2FG、△C2HC、 ‎ ‎△FBE均是等腰直角三角形，四边形AC2B‎2F是平行四边形 ‎ ‎ ∵ AB==2‎ ‎ ∴ 当α=45°时，CE=CD=AB=1‎ 情形①：当0＜x＜1时（如图②所示），‎ ‎△A2B‎2C2与△ABC的重叠部分为五边形C2HEFG ‎ ‎（法一） S五边形C2HEFG=S平行四边形AC2B‎2FSRt△AC‎2GSRt△HB2E ‎∵ C‎2C=x ‎∴ CH=x，AC2=，B2E=HE=‎ ‎∴ AG=C‎2G=AC2=‎ ‎∴ S平行四边形AC2B‎2F=AC2·CE=（）·1=‎ ‎ SRt△AC‎2G=·AG2=‎ ‎ SRt△HB2E=·B2E2= ‎ ‎∴ S五边形C2HEFG=‎ ‎ = ‎ ‎（法二） S五边形C2HEFG= SRt△A2B‎2C2SRt△A2FGSRt△HB2E ‎∵ C‎2C=x ‎∴ AC2=，B2E=‎ ‎∴ C‎2G=AC2=‎ A‎2G=A‎2C2‎C‎2G =‎ ‎∴ SRt△A2B‎2C2=A2==1‎ ‎ SRt△A2FG=A‎2G2=‎ ‎ SRt△HB2E =B2E2= ‎ ‎∴ S五边形C2HEFG=‎ ‎ = ‎ ‎（法三） S五边形C2HEFG= SRt△ABCSRt△AC‎2GSRt△C2HCSRt△FBE ‎∵ C‎2C=x ‎∴ AC2=，CH=，BE=‎ ‎∴ AG=C‎2G=AC2=‎ ‎∴ SRt△ABC=A==1‎ ‎ SRt△ AC‎2G =AG2=‎ ‎ SRt△C2HC =C‎2C2=‎ ‎ SRt△FBE =BE2= ‎ ‎∴ S五边形C2HEFG=‎ ‎ = ‎ 情形②：当1≤x＜时（如图③所示）， ‎ ‎△A2B‎2C2与△ABC的重叠部分为直角梯形C2B2FG ‎ ‎（法一） S直角梯形C2B2FG ‎=S平行四边形C2B2FASRt△AC‎2G ‎=AC2·CEAG2‎ ‎=‎ ‎= ‎ ‎（法二） S直角梯形C2B2FG ‎= SRt△A2B‎2C2SRt△A2FG ‎=‎ ‎=‎ ‎（2010福州）如图，在△ABC中，，，高，矩形EFPQ的一边QP在BC边上，E、F两点分别在AB、AC上，AD交EF于点H。‎ ‎（1）求证：;‎ ‎（2）设，当为何值时，矩形EFPQ的面积最大？并求其最大值;‎ ‎（3）当矩形EFPQ的面积最大时，该矩形EFPQ以每秒1个单位的速度沿射线QC匀速运动（当点Q与点C重合时停止运动），设运动时间为秒，矩形EFPQ与△ABC重叠部分的面积为S，求S和t的函数关系式。‎ A B C P D Q E F 答案：‎ A B C P D Q E F M N 解：（1）∵四边形EFPQ是矩形，∴EF∥QP ‎ ∴△AEF∽△ABC ‎ 又∵AD⊥BC，∴AH⊥EF ‎ ∴‎ ‎ （2）由（1）得，∴‎ ‎ ∴‎ A B C P D Q E F M N ‎ ∴‎ ‎ ∵，∴当时，有最大值，最大值为20。‎ ‎ （3）如图1，由（2）得，‎ ‎ ∵，∴△FPC是等腰直角三角形 ‎ ∴，‎ ‎ 分三种情况讨论：‎ ‎① 如图2，当时，‎ ‎ 设EF、PF分别交AC于点M、N，则△MFN是等腰直角三角形。‎ ‎ ∴‎ ‎ ∴‎ ‎② 如图3，当时，则，‎ ‎ ∴‎ ‎③ 如图4，当时，设EQ交AC于点K ‎ 则 A B C P D Q E F M ‎ ∴‎ 综上所述：S与t的函数关系式为 ‎ ‎ ‎2010丽水 ‎(第10题)‎ A B C D 10. 如图，四边形ABCD中，∠BAD=∠ACB=90°，AB=AD，AC=4BC，设CD的长为x，四边形ABCD的面积为y，则y与x之间的函数关系式是 A． B． ‎ C． D．‎ 答案： C 随州市2010 25．（15分）已知抛物线顶点为C（1，1）且过原点O.过抛物线上一点P（x，y）向直线作垂线，垂足为M，连FM（如图）.‎ ‎（1）求字母a，b，c的值；‎ ‎（2）在直线x＝1上有一点，求以PM为底边的等腰三角形PFM的P点的坐标，并证明此时△PFM为正三角形；‎ ‎（3）对抛物线上任意一点P，是否总存在一点N（1，t），使PM＝PN恒成立，若存在请求出t值，若不存在请说明理由.‎ 答案：25．（1）a＝－1，b＝2，c＝0‎ ‎（2）过P作直线x=1的垂线，可求P的纵坐标为，横坐标为.此时，MP＝MF＝PF＝1，故△MPF为正三角形.‎ ‎（3）不存在.因为当t＜，x＜1时，PM与PN不可能相等，同理，当t＞，x＞1时，PM与PN不可能相等.‎ ‎（2010哈尔滨）１．如图，在△ABC中，∠ACB＝90°，AC＝BC＝10，在△DCE中，‎ ‎∠DCE＝90°，DC＝EC＝6，点D在线段AC上，点E在线段BC 的延长线上．将△DCE绕点C旋转60°得到△D′CE′（点D的 对应点为点D′，点E的对应点为点 E′），连接AD′、BE′，‎ 过点C作CN⊥ BE′，垂足为N，直线CN交线段AD′于点M，‎ 则MN的长为 ．‎ ‎（2010哈尔滨）２．如图，在平面直角坐标系中，点O是坐标原点，四边形AOCB是梯形，AB∥OC，点A的坐标为（0，8），点C的坐标为（10，0），OB＝OC．‎ ‎ （1）求点B的坐标；‎ ‎ （2）点P从C点出发，沿线段CO以5个单位/秒的速度向终点O匀速运动，过点P作PH⊥OB，垂足为H，设△HBP的面积为S（S≠0），点P的运动时间为t秒，求S与t之间的函数关系式（直接写出自变量t的取值范围）；‎ ‎ （3）在（2）的条件下，过点P作PM∥CB交线段AB于点M，过点M作MR⊥OC，垂足为R，线段MR分别交直线PH、OB于点E、G，点F为线段PM的中点，连接EF，当t为何值时，？‎ ‎ ‎ ‎ (2010台州市) 22．类比学习：一动点沿着数轴向右平移3个单位，再向左平移2个单位，相当于向右平移1个单位．用实数加法表示为 3+（）=1．‎ ‎ 　　若坐标平面上的点作如下平移：沿x轴方向平移的数量为a（向右为正，向左为负，平移个单位），沿y轴方向平移的数量为b（向上为正，向下为负，平移个单位），则把有序数对{a，b}叫做这一平移的“平移量”；“平移量”{a，b}与“平移量”{c，d}的加法运算法则为．‎ ‎ 解决问题：（1）计算：{3，1}+{1，2}；{1，2}+{3，1}．‎ ‎ （2）①动点P从坐标原点O出发，先按照“平移量”{3，1}平移到A，再按照“平移量”‎ ‎{1，2}平移到B；若先把动点P按照“平移量”{1，2}平移到C，再按照“平移量”‎ ‎{3，1}平移，最后的位置还是点B吗? 在图1中画出四边形OABC.‎ ‎②证明四边形OABC是平行四边形.‎ ‎（3）如图2，一艘船从码头O出发，先航行到湖心岛码头P（2，3），再从码头P航行到码头Q（5，5），最后回到出发点O. 请用“平移量”加法算式表示它的航行过程．‎ ‎（第22题）‎ y O 图2‎ Q（5, 5）‎ P（2, 3）‎ y O 图1‎ ‎1‎ ‎1‎ x x 解：（1）{3，1}+{1，2}={4，3}． ……………………………………………2分 y O ‎1‎ ‎1‎ x A B C ‎{1，2}+{3，1}={4，3}． …………………………………………………………………2分 ‎（2）①画图 …………………………………………………2分 ‎ 最后的位置仍是B．……………………………………1分 ‎② 证明：由①知，A（3，1），B(4，3)，C（1，2）‎ ‎∴OC=AB==，OA=BC==，‎ ‎ ∴四边形OABC是平行四边形．…………………………3分 ‎（3）{2，3}+{3，2}+{-5，-5}={0, 0}．……………………2分 ‎（2010河南）19．（9分）如图，在梯形ABCD中，AD//BC，E是BC的中点，AD=5，BC=12，CD=，∠C=45°，点P是BC边上一动点，设PB的长为x．‎ ‎（1）当x的值为____________时，以点P、A、D、E为顶点的四边形为直角梯形；‎ ‎（2）当x的值为____________时，以点P、A、D、E为顶点的四边形为平行四边形；；‎ ‎（3）点P在BC边上运动的过程中，以P、A、D、E为顶点的四边形能否构成菱形？试说明理由．‎ ‎(1)3或8‎ ‎(2) 1或11‎ ‎(3)由(2)可知，当BP=11时，以点P、A、D、E为顶点的四边形是平行四边形 ‎∴EP=AD=5 过D作DF⊥BC于F，则DF=FC=4，∴FP=3 ∴ DP=5‎ ‎∴EP=DP 故此时□PDAE是菱形 即以点P、A、D、E为顶点的四边形能构成菱形。‎ ‎（2010广东中山）22．如图（1），（2）所示，矩形ABCD的边长AB=6，BC=4，点F在DC上，DF=2。动点M、N分别 从点D、B同时出发，沿射线DA、线段BA向点A的方向运动（点M可运动到DA的延长线上），‎ 当动点N运动到点A时，M、N两点同时停止运动。连接FM、FN，当F、N、M不在同一直线时，‎ 可得△FMN，过△FMN三边的中点作△PQW。设动点M、N的速度都是1个单位/秒，M、N运动的 时间为x秒。试解答下列问题：‎ ‎（1）说明△FMN∽△QWP；‎ ‎（2）设0≤x≤4（即M从D到A运动的时间段）。试问x为何值时，△PQW为直角三角形？‎ 当x在何范围时，△PQW不为直角三角形？‎ ‎（3）问当x为何值时，线段MN最短？求此时MN的值。‎ 第22题图（2）‎ A B C D F M N W P Q 第22题图（1）‎ A B M C F D N W P Q ‎22、（1）提示：∵PQ∥FN，PW∥MN ∴∠QPW =∠PWF，∠PWF =∠MNF ‎ ‎∴∠QPW =∠MNF ‎ 同理可得：∠PQW =∠NFM或∠PWQ =∠NFM ∴△FMN∽△QWP ‎ ‎（2）当时，△PQW为直角三角形；‎ 当0≤x<，时，连结C′C，设四边形ACC′A ′的面积为S，求S关于t的函数关系式；‎ ‎②当线段A ′C ′与射线BB，有公共点时，求t的取值范围(写出答案即可)．‎ ‎（2010·浙江湖州）25．如图，已知在矩形ABCD中，AB＝2，BC＝3，P是线段AD边上的任意一点（不含端点A、D），连结PC， 过点P作PE⊥PC交AB于E ‎（1）在线段AD上是否存在不同于P的点Q，使得QC⊥QE？若存在，求线段AP与AQ之间的数量关系；若不存在，请说明理由；‎ A B C 第25题 D P E ‎（2）当点P在AD上运动时，对应的点E也随之在AB上运动，求BE的取值范围．‎ ‎（此题没有给答案）‎