中考数学试题分类汇编综合型问题

中考数学试题分类汇编综合型问题

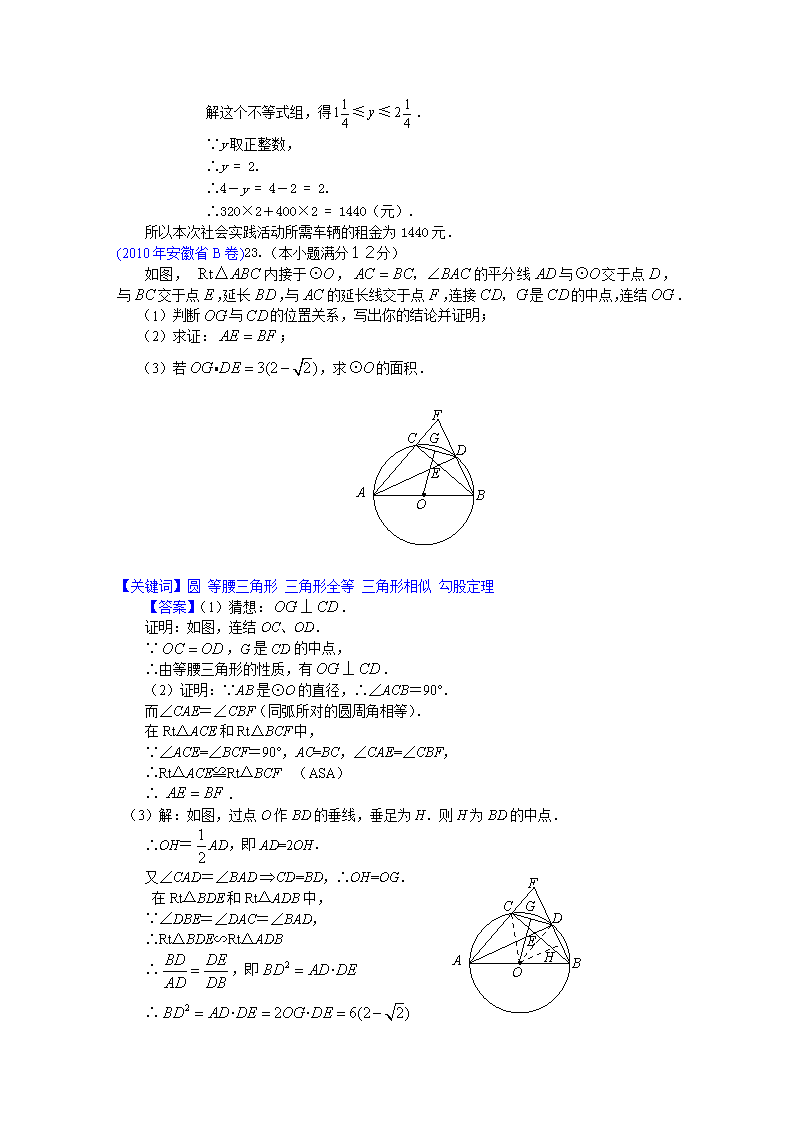
‎2010年中考数学试题分类汇编 综合型问题 ‎20、（2010年浙江省东阳县）如图，BD为⊙O的直径，点A是弧BC的中点，AD交BC于E点，AE=2，ED=4. ‎ ‎（1）求证: ～；‎ ‎(2) 求的值； ‎ ‎（3）延长BC至F，连接FD，使的面积等于，‎ 求的度数.‎ ‎【关键词】圆、相似三角形、三角形函数问题 ‎【答案】（１）∵点A是弧BC的中点　∴∠ＡＢＣ＝∠ＡＤＢ 又∵∠ＢＡＥ＝∠ＢＡＥ　　∴△ＡＢＥ∽△ＡＢＤ ‎（２）∵△ＡＢＥ∽△ＡＢＤ　∴ＡＢ２＝２×６＝１２　∴ＡＢ＝２‎ 在Ｒｔ△ＡＤＢ中，ｔａｎ∠ＡＤＢ＝‎ ‎（３）连接ＣＤ，可得ＢＦ＝８，ＢＥ＝４，则ＥＦ＝４，△ＤＥＦ是正三角形，‎ ‎∠ＥＤＦ＝６０°‎ ‎20．（2010年山东省青岛市）某学校组织八年级学生参加社会实践活动，若单独租用35座客车若干辆，则刚好坐满；若单独租用55座客车，则可以少租一辆，且余45个空座位．‎ ‎（1）求该校八年级学生参加社会实践活动的人数；‎ ‎（2）已知35座客车的租金为每辆320元，55座客车的租金为每辆400元．根据租车资金不超过1500元的预算，学校决定同时租用这两种客车共4辆（可以坐不满）．请你计算本次社会实践活动所需车辆的租金．‎ ‎【关键词】不等式与方程问题 ‎【答案】解：（1）设单独租用35座客车需x辆，由题意得：‎ ‎,‎ 解得：.‎ ‎∴（人）. ‎ 答：该校八年级参加社会实践活动的人数为175人． 3分 ‎（2）设租35座客车y辆，则租55座客车（）辆，由题意得： ‎ ‎， 6分 解这个不等式组，得．‎ ‎∵y取正整数，‎ ‎∴y = 2.‎ ‎∴4－y = 4－2 = 2.‎ ‎∴320×2＋400×2 = 1440（元）.‎ 所以本次社会实践活动所需车辆的租金为1440元．‎ ‎(2010年安徽省B卷)23.（本小题满分１２分）‎ 如图， 内接于，的平分线与交于点，与交于点，延长，与的延长线交于点，连接是的中点，连结．‎ ‎（1）判断与的位置关系，写出你的结论并证明；‎ ‎（2）求证：；‎ ‎（3）若，求的面积．‎ F D G E B C A O ‎【关键词】圆 等腰三角形 三角形全等 三角形相似 勾股定理 ‎【答案】（1）猜想：．‎ 证明：如图，连结OC、OD．‎ ‎∵，G是CD的中点，‎ ‎∴由等腰三角形的性质，有．‎ ‎（2）证明：∵AB是⊙O的直径，∴∠ACB＝90°．‎ 而∠CAE＝∠CBF（同弧所对的圆周角相等）．‎ 在Rt△ACE和Rt△BCF中，‎ ‎∵∠ACE=∠BCF＝90°，AC=BC，∠CAE=∠CBF，‎ ‎∴Rt△ACE≌Rt△BCF （ASA）‎ ‎∴． ‎ ‎ （3）解：如图，过点O作BD的垂线，垂足为H．则H为BD的中点．‎ ‎∴OH＝AD，即AD=2OH．‎ F D G E B C A O H 又∠CAD＝∠BADCD=BD，∴OH=OG．‎ ‎ 在Rt△BDE和Rt△ADB中，‎ ‎∵∠DBE＝∠DAC＝∠BAD，‎ ‎∴Rt△BDE∽Rt△ADB ‎∴，即 ‎∴‎ 又，∴．‎ ‎∴ … ① ‎ 设，则，AB=．‎ ‎∵AD是∠BAC的平分线，‎ ‎∴．‎ 在Rt△ABD和Rt△AFD中，‎ ‎∵∠ADB=∠ADF＝90°，AD=AD，∠FAD＝∠BAD，‎ ‎∴Rt△ABD≌Rt△AFD（ASA）．‎ ‎∴AF=AB=，BD=FD．‎ ‎∴CF=AF-AC=‎ 在Rt△BCF中，由勾股定理，得 ‎ …② ‎ 由①、②，得．‎ ‎∴．解得或（舍去）．‎ ‎∴‎ ‎∴⊙O的半径长为． ‎ ‎∴ ‎ A C x y B O ‎(2010年安徽省B卷)24.（本小题满分12分）‎ 已知：抛物线的对称轴为与轴交于两点，与轴交于点其中、‎ ‎（1）求这条抛物线的函数表达式．‎ ‎（2）已知在对称轴上存在一点P，使得的周长最小．请求出点P的坐标．‎ ‎（3）若点是线段上的一个动点（不与点O、点C重合）．过点D作交轴于点连接、．设的长为，的面积为．求与之间的函数关系式．试说明是否存在最大值，若存在，请求出最大值；若不存在，请说明理由．‎ ‎【关键词】二次函数解析式 对称点 相似三角形 三角形面积 ‎【答案】（1）由题意得 解得 ‎∴此抛物线的解析式为 ‎（2）连结、.因为的长度一定，所以周长最小，就是使最小.点关于对称轴的对称点是点，与对称轴的交点即为所求的点.‎ O A C x y B E P D 设直线的表达式为 则 解得 ‎∴此直线的表达式为 把代入得 ‎∴点的坐标为 ‎（3）存在最大值 理由：∵即 ‎∴‎ ‎∴即 ‎∴‎ 连结 ‎ =‎ ‎=‎ ‎∵‎ ‎∴当时，‎ A O x B C M y ‎（2010年福建省晋江市）已知：如图，把矩形放置于直角坐标系中，， ，取的中点，连结，把沿轴的负方向平移的长度后得到.‎ ‎(1)试直接写出点的坐标；‎ ‎(2)已知点与点在经过原点的抛物线上，点在第一象限内的该抛物线上移动，过点作轴于点，连结.‎ ‎①若以、、为顶点的三角形与相似，试求出点的坐标；‎ ‎②试问在抛物线的对称轴上是否存在一点，使得的值最大.‎ ‎【关键词】二次函数、相似三角形、最值问题 A O x D B C M y E P T Q 答案：解：(1)依题意得：；‎ ‎ (2) ① ∵，，‎ ‎∴.‎ ‎ ∵抛物线经过原点，‎ ‎∴设抛物线的解析式为 又抛物线经过点与点 ‎∴ 解得：‎ ‎∴抛物线的解析式为.‎ ‎∵点在抛物线上，‎ ‎∴设点.‎ ‎1)若∽，则， ，解得：(舍去)或，‎ ‎∴点.‎ ‎2)若∽，则， ，解得：(舍去)或，‎ ‎∴点.‎ ‎②存在点，使得的值最大.‎ 抛物线的对称轴为直线，设抛物线与轴的另一个交点为，则点.‎ ‎∵点、点关于直线对称，‎ ‎∴‎ 要使得的值最大，即是使得的值最大，‎ 根据三角形两边之差小于第三边可知，当、、三点在同一直线上时，的值最大. ‎ 设过、两点的直线解析式为，‎ ‎∴ 解得：‎ ‎∴直线的解析式为.‎ 当时，.‎ ‎∴存在一点使得最大. ‎ ‎2. （2010年福建省晋江市）如图，在等边中，线段为边上的中线. 动点在直线上时，以为一边且在的下方作等边，连结.‎ ‎(1) 填空：度；‎ ‎(2) 当点在线段上(点不运动到点)时，试求出的值；‎ ‎(3)若，以点为圆心，以5为半径作⊙与直线相交于点、两点，在点运动的过程中(点与点重合除外)，试求的长.‎ A B C 备用图(1)‎ A B C 备用图(2)‎ ‎【关键词】三角形全等、等边三角形、垂径定理 答案： (1)60； ‎ ‎(2)∵与都是等边三角形 ‎∴，，‎ ‎∴‎ ‎∴‎ ‎∴≌‎ ‎∴，∴.‎ ‎ (3)①当点在线段上（不与点重合）时，由(2)可知≌，则，作于点，则，连结，则.‎ 在中，，，则.‎ 在中，由勾股定理得：，则.‎ ‎②当点在线段的延长线上时，∵与都是等边三角形 ‎∴，，‎ ‎∴‎ ‎∴‎ ‎∴≌‎ ‎∴，同理可得：.‎ ‎③当点在线段的延长线上时，‎ ‎∵与都是等边三角形 ‎∴，，‎ ‎∴‎ ‎∴‎ ‎∴≌‎ ‎∴‎ ‎∵‎ ‎∴‎ ‎∴.‎ 同理可得：.‎ 综上，的长是6. ‎ C O A B D N M P x y ‎1.（2010年浙江省东阳市）如图，P为正方形ABCD的对称中心，A（0，3），B（1，0），直线OP交AB于N，DC于M，点H从原点O出发沿x轴的正半轴方向以1个单位每秒速度运动，同时，点R从O出发沿OM方向以个单位每秒速度运动，运动时间为t。求：‎ ‎（1）C的坐标为 ▲ ；‎ ‎（2）当t为何值时，△ANO与△DMR相似？‎ ‎（3）△HCR面积S与t的函数关系式；‎ 并求以A、B、C、R为顶点的四边形是梯形 时t的值及S的最大值。‎ C O A B D N M P x y R H 关键词：相似三角形、动态问题、二次函数 答案：（1）Ｃ（４，１）‎ ‎（2）当∠MDR＝45０时，ｔ＝2,点Ｈ（2，0）‎ 当∠DRM＝45０时，ｔ＝3,点Ｈ（3，0）‎ ‎（３）Ｓ＝－ｔ2＋２ｔ（０＜ｔ≤４）；Ｓ＝ｔ2－２ｔ（ｔ＞４）‎ 当ＣＲ∥ＡＢ时，ｔ＝， Ｓ＝ ‎ 当ＡＲ∥ＢＣ时，ｔ＝， Ｓ＝ ‎ 当ＢＲ∥ＡＣ时，ｔ＝， Ｓ＝ ‎ x O P y ‎1、（2010年宁波市）如图，已知⊙P的半径为2，圆心P在抛物线上运动，当⊙P与轴相切时，圆心P的坐标为___________。‎ ‎【关键词】直线与圆的位置关系，二次函数 ‎【答案】‎ ‎（，2）或（，2）（对珍一个得2分）‎ ‎2、（2010年宁波市）如图1、在平面直角坐标系中，O是坐标原点，□ABCD的顶点A的坐标为（－2，0），点D的坐标为（0，），点B在轴的正半轴上，点E为线段AD的中点，过点E的直线与轴交于点F，与射线DC交于点G。‎ ‎（1）求的度数;‎ ‎（2）连结OE，以OE所在直线为对称轴，△OEF经轴对称变换后得到△，记直线与射线DC的交点为H。‎ ‎①如图2，当点G在点H的左侧时，求证：△DEG∽△DHE;‎ y x C D A O B E G F ‎（图1）‎ x C D A O B E G H F y ‎（图2）‎ x C D A O B E y ‎（图3）‎ ‎②若△EHG的面积为，请直接写出点F的坐标。‎ ‎【关键词】平行四边形，相似 ‎【答案】‎ 解：（1）‎ ‎ （2）（2，）‎ ‎ （3）①略 ‎ ②过点E作EM⊥直线CD于点M ‎∵CD∥AB x C D A O B E y ‎（图3）‎ Ｍ ‎∴‎ ‎∴‎ ‎∵‎ ‎∴‎ ‎∵△DHE∽△DEG ‎∴即 当点H在点G的右侧时，设，‎ ‎∴‎ 解：‎ ‎∴点F的坐标为（，0）‎ 当点H在点Ｇ的左侧时，设，‎ ‎∴‎ 解：，（舍）‎ ‎∵△ＤＥＧ≌△ＡＥＦ ‎∴‎ ‎∵‎ ‎∴点Ｆ的坐标为（，0）‎ 综上可知，点Ｆ的坐标有两个，分别是（，0），（，0）‎ ‎（2010辽宁省丹东市）．如图，已知在⊙O中，AB=4，AC是⊙O的直径，AC⊥BD于F，∠A=30°．‎ ‎（1）求图中阴影部分的面积；‎ ‎（2）若用阴影扇形OBD围成一个圆锥侧面，请求出这个圆锥的底面圆的半径．‎ F 第22题图 ‎【关键词】圆锥侧面积 ‎【答案】‎ 解：（1）法一：过O作OE⊥AB于E，‎ 则AE=AB=2． 1分 F E ‎ 在RtAEO中，∠BAC=30°，cos30°=．‎ ‎∴OA===4． …………………………3分 又∵OA=OB，∴∠ABO=30°．∴∠BOC=60°． ‎ ‎∵AC⊥BD，∴．‎ ‎∴∠COD =∠BOC=60°．∴∠BOD=120°． 5分 ‎∴S阴影==． 6分 法二：连结AD． 1分 ‎∵AC⊥BD，AC是直径，‎ F ‎∴AC垂直平分BD． ……………………2分 ‎∴AB=AD，BF=FD，． ‎ ‎∴∠BAD=2∠BAC=60°，‎ ‎∴∠BOD=120°． ……………………3分 ‎∵BF=AB=2，sin60°=，‎ AF=AB·sin60°=4×=6．‎ ‎∴OB2=BF2+OF2．即．‎ ‎∴OB=4． 5分 ‎∴S阴影=S圆=． 6分 法三：连结BC．………………………………………………………………………………1分 ‎ ∵AC为⊙O的直径， ∴∠ABC=90°．‎ F ‎∵AB=4，‎ ‎∴． ……………………3分 ‎∵∠A=30°， AC⊥BD， ∴∠BOC=60°， ‎ ‎∴∠BOD=120°．‎ ‎∴S阴影=π·OA2=×42·π=．……………………6分 以下同法一．‎ ‎（2）设圆锥的底面圆的半径为r，则周长为2πr，‎ ‎ ∴． ‎ ‎∴． ‎ ‎（2010辽宁省丹东市）．如图，平面直角坐标系中有一直角梯形OMNH，点H的坐标为（－8，0），点N的坐标为（－6，－4）．‎ ‎（1）画出直角梯形OMNH绕点O旋转180°的图形OABC，并写出顶点A，B，C的坐标（点M的对应点为A， 点N的对应点为B， 点H的对应点为C）；‎ ‎（2）求出过A，B，C三点的抛物线的表达式； ‎ ‎（3）截取CE=OF=AG=m，且E，F，G分别在线段CO，OA，AB上，求四边形BEFG的面积S与m之间的函数关系式，并写出自变量m的取值范围；面积S是否存在最小值?若存在，请求出这个最小值；若不存在，请说明理由；‎ ‎ （4）在（3）的情况下，四边形BEFG是否存在邻边相等的情况，若存在，请直接写出此时m的值，并指出相等的邻边；若不存在，说明理由．‎ ‎【关键词】旋转抛物线的表达式；存在性问题 ‎【答案】（1） 利用中心对称性质，画出梯形OABC． 1分 ‎∵A，B，C三点与M，N，H分别关于点O中心对称，‎ ‎∴A（0，4），B（6，4），C（8，0） 3分 ‎（写错一个点的坐标扣1分）‎ O M N H A C E F D B ‎↑‎ ‎→‎ ‎－8‎ ‎(－6，－4)‎ x y ‎（2）设过A，B，C三点的抛物线关系式为，‎ ‎∵抛物线过点A（0，4）， ‎ ‎∴．则抛物线关系式为． 4分 将B（6，4）， C（8，0）两点坐标代入关系式，得 ‎ 5分 ‎ 解得 6分 所求抛物线关系式为：． 7分 ‎（3）∵OA=4，OC=8，∴AF=4－m，OE=8－m． 8分 ‎ ∴ ‎ ‎ OA（AB+OC）AF·AGOE·OFCE·OA ‎ ‎ ‎ （ 0＜＜4） 10分 ‎∵． ∴当时，S的取最小值．‎ 又∵0＜m＜4，∴不存在m值，使S的取得最小值． 12分 ‎（4）当时，GB=GF，当时，BE=BG． 14分 ‎（2010江苏宿迁）（本题满分12分）已知抛物线交x轴于A(1,0)、B(3,0)‎ 两点，交y轴于点C，其顶点为D． ‎ ‎（1）求b、c的值并写出抛物线的对称轴；‎ ‎（2）连接BC，过点O作直线OE⊥BC交抛物线的对称轴于点E．‎ 求证：四边形ODBE是等腰梯形；‎ ‎（3）抛物线上是否存在点Q，使得△OBQ的面积等于四边形ODBE的面积的？若存在，求点Q的坐标；若不存在，请说明理由．‎ ‎【关键词】抛物线关系式及图形的存在性问题 ‎【答案】（1）求出：，，抛物线的对称轴为：x=2 ………………3分 ‎(2) 抛物线的解析式为，易得C点坐标为（0，3），D点坐标为（2，-1）‎ 设抛物线的对称轴DE交x轴于点F，易得F点坐标为（2，0），连接OD，DB，BE ‎∵OBC是等腰直角三角形，DFB也是等腰直角三角形，E点坐标为（2，2），‎ ‎∴∠BOE= ∠OBD= ∴OE∥BD ‎∴四边形ODBE是梯形 ………………5分 在和中，‎ OD= ，BE=‎ ‎∴OD= BE ‎∴四边形ODBE是等腰梯形 ………………7分 ‎(3) 存在， ………………8分 由题意得： ………………9分 设点Q坐标为（x，y），‎ 由题意得：=‎ ‎∴‎ 当y=1时，即，∴ ， ，‎ ‎∴Q点坐标为（2+，1）或(2-，1) ………………11分 当y=-1时，即， ∴x=2，‎ ‎∴Q点坐标为（2，-1）‎ 综上所述，抛物线上存在三点Q（2+，1），Q (2-，1) ，Q（2，-1）‎ 使得=． ………………12分 E F Q1‎ Q3‎ Q2‎ ‎ (2010年浙江省绍兴市)如图,设抛物线C1:, C2:,C1与C2的交点为A, B,点A的坐标是,点B的横坐标是－2.‎ 第24题图 ‎ （1）求的值及点B的坐标； ‎ ‎（2）点D在线段AB上,过D作x轴的垂线,垂足为点H,‎ 在DH的右侧作正三角形DHG. 记过C2顶点Ｍ的 直线为,且与x轴交于点N.‎ ‎① 若过△DHG的顶点G,点D的坐标为 ‎(1, 2)，求点N的横坐标；‎ ‎② 若与△DHG的边DG相交,求点N的横 坐标的取值范围.‎ ‎【答案】解：（1）∵ 点A在抛物线C1上，∴ 把点A坐标代入得 =1. ‎ ‎∴ 抛物线C1的解析式为,‎ ‎ 设B(－2,b)， ∴ b＝－4, ∴ B(－2,－4) . ‎ ‎（2）①如图1，‎ ‎∵ M(1, 5)，D(1, 2), 且DH⊥x轴，∴ 点M在DH上，MH=5. ‎ 过点G作GE⊥DH,垂足为E,‎ 由△DHG是正三角形,可得EG=, EH=1，‎ ‎∴ ME＝4. ‎ 第24题图1‎ 设N ( x, 0 ), 则 NH＝x－1,‎ 由△MEG∽△MHN,得 ,‎ ‎∴ , ∴ ,‎ ‎∴ 点N的横坐标为． ‎ ‎② 当点Ｄ移到与点A重合时,如图2，‎ 第24题图2‎ 直线与DG交于点G,此时点Ｎ的横坐标最大．‎ 过点Ｇ,Ｍ作x轴的垂线,垂足分别为点Ｑ,F,‎ 设Ｎ（x，0），‎ ‎∵ A (2, 4), ∴ G (, 2),‎ ‎∴ NQ=，ＮF =, GQ=2, MF =5.‎ ‎∵ △NGQ∽△NMF，‎ ‎∴ ,‎ ‎∴ ,‎ 第24题图3‎ 图4‎ ‎∴ . ‎ 当点D移到与点B重合时,如图3，‎ 直线与DG交于点D,即点B, ‎ 此时点N的横坐标最小.‎ ‎ ∵ B(－2, －4), ∴ H(－2, 0), D(－2, －4),‎ 设N（x，0）， ‎ ‎∵ △BHN∽△MFN， ∴ ，‎ ‎∴ , ∴ . ‎ ‎∴ 点N横坐标的范围为 ≤x≤. ‎ ‎（2010年宁德市）（本题满分13分）如图，在梯形ABCD中，AD∥BC，∠B＝90°，BC＝6，AD＝3，∠DCB＝30°.点E、F同时从B点出发，沿射线BC向右匀速移动.已知F点移动速度是E点移动速度的2倍，以EF为一边在CB的上方作等边△EFG．设E点移动距离为x（x＞0）.‎ ‎⑴△EFG的边长是____（用含有x的代数式表示），当x＝2时，点G的位置在_______；‎ ‎⑵若△EFG与梯形ABCD重叠部分面积是y，求 ‎①当0＜x≤2时，y与x之间的函数关系式；‎ ‎②当2＜x≤6时，y与x之间的函数关系式；‎ ‎⑶探求⑵中得到的函数y在x取含何值时，存在最大值，并求出最大值.‎ B E→ F→ C A D G ‎【答案】解：⑴ x，D点；‎ ‎⑵ ①当0＜x≤2时，△EFG在梯形ABCD内部，所以y＝x2；‎ ‎②分两种情况：‎ Ⅰ.当2＜x＜3时，如图1，点E、点F在线段BC上，‎ ‎△EFG与梯形ABCD重叠部分为四边形EFNM，‎ ‎∵∠FNC＝∠FCN＝30°,∴FN＝FC＝6－2x.∴GN＝3x－6.‎ 由于在Rt△NMG中，∠G＝60°，‎ 所以，此时 y＝x2－（3x－6）2＝.‎ Ⅱ.当3≤x≤6时，如图2，点E在线段BC上，点F在射线CH上，‎ ‎△EFG与梯形ABCD重叠部分为△ECP，‎ ‎∵EC＝6－x,‎ ‎∴y＝（6－x）2＝.‎ ‎⑶当0＜x≤2时，∵y＝x2在x＞0时，y随x增大而增大，‎ ‎∴x＝2时，y最大＝；‎ 当2＜x＜3时，∵y＝在x＝时，y最大＝；‎ 当3≤x≤6时，∵y＝在x＜6时，y随x增大而减小，‎ B E C F A D G P H 图2‎ ‎∴x＝3时，y最大＝.‎ 综上所述：当x＝时，y最大＝.‎ B E F C A D G N M 图1‎ ‎24．（2010浙江省喜嘉兴市）如图，已知抛物线y＝－x2＋x＋4交x轴的正半轴于点A，交y轴于点B．‎ ‎（1）求A、B两点的坐标，并求直线AB的解析式；‎ ‎（2）设P（x，y）（x＞0）是直线y＝x上的一点，Q是OP的中点（O是原点），以PQ为对角线作正方形PEQF，若正方形PEQF与直线AB有公共点，求x的取值范围；‎ ‎（3）在（2）的条件下，记正方形PEQF与△OAB公共部分的面积为S，求S关于x的函数解析式，并探究S的最大值．‎ ‎【关键词】一元二次方程、一次函数、二次函数、‎ ‎【答案】‎ ‎（1）令，得，即，‎ 解得，，所以．令，得，所以．‎ 设直线AB的解析式为，则，解得，‎ 所以直线AB的解析式为． …5分 ‎（2）当点在直线AB上时，，解得，‎ 当点在直线AB上时，，解得．‎ 所以，若正方形PEQF与直线AB有公共点，则． …4分 ‎（3）当点在直线AB上时，（此时点F也在直线AB上）‎ ‎，解得．‎ ‎①当时，直线AB分别与PE、PF有交点，设交点分别为C、D，‎ 此时，，‎ 又，‎ ‎（第24题）‎ 所以，‎ 从而，‎ ‎．‎ 因为，所以当时，．‎ ‎②当时，直线AB分别与QE、QF有交点，设交点分别为M、N，‎ ‎（第24题 备用）‎ 此时，，‎ 又，‎ 所以，‎ 即．‎ 其中当时，．‎ 综合①②得，当时，． …5分 ‎23(2010年浙江省金华). (本题10分）‎ 已知点P的坐标为（m，0），在x轴上存在点Q（不与P点重合），以PQ为边作正方形PQMN，使点M落在反比例函数y = 的图像上.小明对上述问题进行了探究，发现不论m取何值，符合上述条件的正方形只有两个，且一个正方形的顶点M在第四象限，另一个正方形的顶点M1在第二象限.‎ ‎（1）如图所示，若反比例函数解析式为y= ，P点坐标为（1， 0），图中已画出一符合条件的一个正方形PQMN，请你在图中画出符合条件的另一个正方形PQ1M1N1，并写出点M1的坐标； ‎ ‎（温馨提示：作图时，别忘了用黑色字迹的钢笔或签字笔描黑喔！）‎ y P Q M N O x ‎1‎ ‎2‎ ‎-1‎ ‎-2‎ ‎-3‎ ‎-3‎ ‎-2‎ ‎-1‎ ‎1‎ ‎2‎ ‎3‎ ‎(第23题图)‎ M1的坐标是 ▲ ‎ ‎ （2） 请你通过改变P点坐标，对直线M1 M的解析式y﹦kx＋b进行探究可得 k﹦ ▲ ， 若点P的坐标为（m，0）时，则b﹦ ▲ ；‎ ‎ （3） 依据(2)的规律，如果点P的坐标为（6，0），请你求出点M1和点M的坐标．‎ M1‎ P Q M N O y ‎1‎ ‎2‎ ‎3‎ ‎-1‎ ‎-2‎ ‎-3‎ ‎-3‎ ‎-2‎ ‎-1‎ ‎1‎ ‎2‎ ‎3‎ Q1‎ N1‎ ‎【关键词】反比例函数、坐标、一次函数 ‎【答案】解：（1）如图；M1 的坐标为（－1，2） ‎ ‎ （2），‎ ‎ （3）由（2）知，直线M1 M的解析式为 ‎ 则(，)满足 ‎ 解得 ，‎ ‎ ∴ ，‎ ‎ ∴M1，M的坐标分别为（，），（，）．‎ ‎24．（2010年浙江台州市）如图，Rt△ABC中，∠C=90°，BC=6，AC=8．点P，Q都是斜边AB上的动点，点P从B 向A运动（不与点B重合），点Q从A向B运动，BP=AQ．点D，E分别是点A，B以Q，P为对称中心的对称点， HQ⊥AB于Q，交AC于点H．当点E到达顶点A时，P，Q同时停止运动．设BP的长为x，△HDE的面积为y．‎ ‎（第24题）‎ H ‎（1）求证：△DHQ∽△ABC；‎ ‎（2）求y关于x的函数解析式并求y的最大值；‎ ‎（3）当x为何值时，△HDE为等腰三角形？‎ ‎ ‎ ‎【关键词】相似三角形、二次函数、等腰三角形 ‎【答案】（1）∵A、D关于点Q成中心对称，HQ⊥AB，‎ ‎∴=90°，HD=HA，‎ ‎∴，‎ ‎（图1）‎ ‎（图2）‎ ‎∴△DHQ∽△ABC． ‎ ‎（2）①如图1，当时， ‎ ED=，QH=，‎ 此时．‎ 当时，最大值．‎ ‎②如图2，当时，‎ ED=，QH=，‎ 此时．当时，最大值．‎ ‎∴y与x之间的函数解析式为 y的最大值是．‎ ‎（3）①如图1，当时，‎ 若DE=DH，∵DH=AH=， DE=，‎ ‎∴=，．‎ 显然ED=EH，HD=HE不可能；‎ 若DE=DH，=，； ‎ 若HD=HE，此时点D，E分别与点B，A重合，；‎ 若ED=EH，则△EDH∽△HDA，‎ ‎∴，，． ‎ ‎∴当x的值为时，△HDE是等腰三角形.‎ ‎（其他解法相应给分）‎ ‎20. （2010年益阳市）如图9，在平面直角坐标系中，已知A、B、C三点的坐标分别为A（－2，0），B（6，0），C（0，3）.‎ ‎(1)求经过A、B、C三点的抛物线的解析式；‎ ‎(2)过Ｃ点作CD平行于轴交抛物线于点D，写出D点的坐标，并求AD、BC的交点E 的坐标；‎ ‎(3)若抛物线的顶点为Ｐ，连结ＰC、ＰD，判断四边形CEDP的形状，并说明理由.‎ ‎【关键词】二次函数、一次函数、菱形的判定 ‎【答案】⑴ 由于抛物线经过点，可设抛物线的解析式为，则，　　　　　　　　　‎ ‎　解得 ‎∴抛物线的解析式为　　　‎ ‎⑵ 的坐标为 ‎ 直线的解析式为 直线的解析式为 ‎　由 ‎　求得交点的坐标为　　　　　　　 ‎ ‎⑶　连结交于，的坐标为 又∵，‎ ‎　　∴，且 ‎　　　　∴四边形是菱形　　　　　　　　　‎