中考数学第20梯形一轮复习学案

中考数学第20梯形一轮复习学案

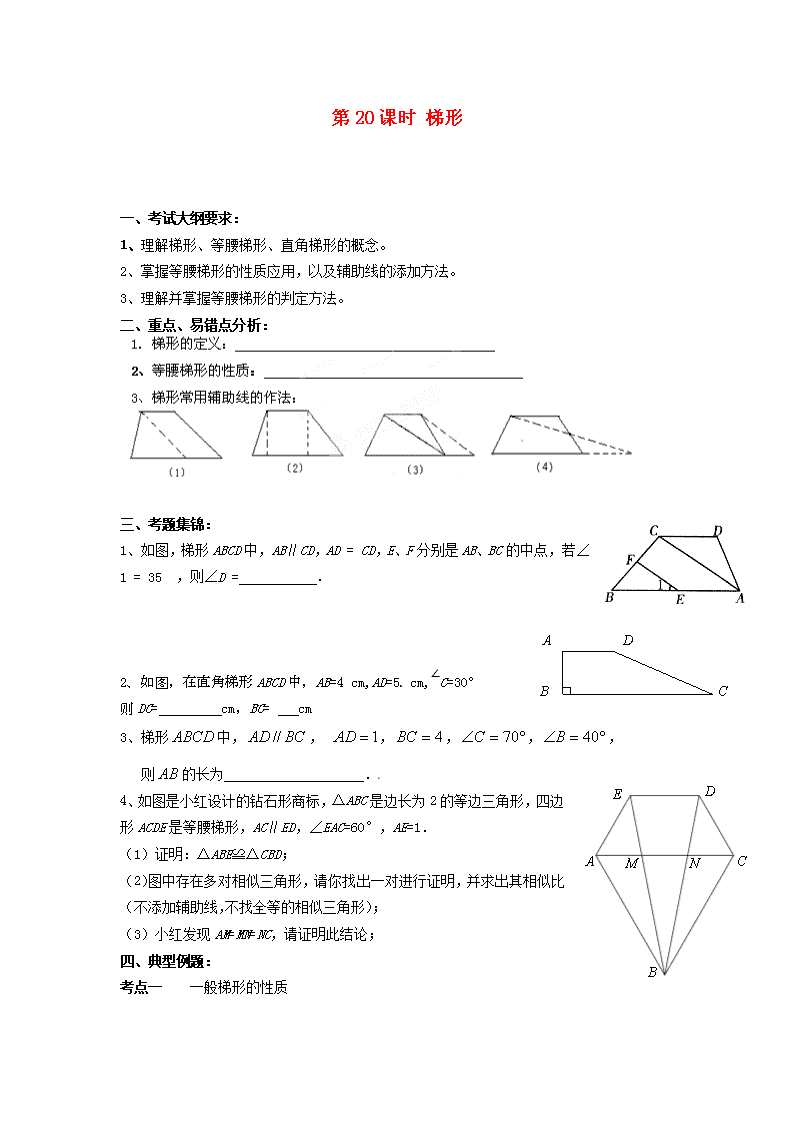
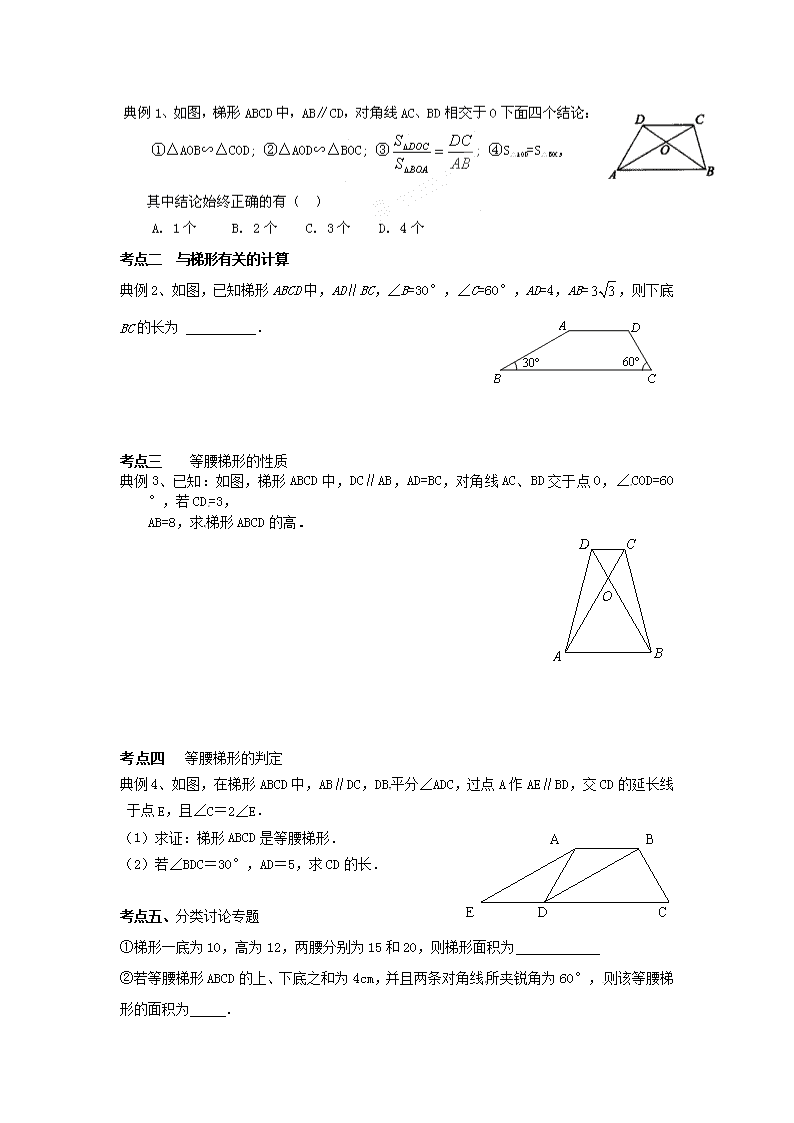
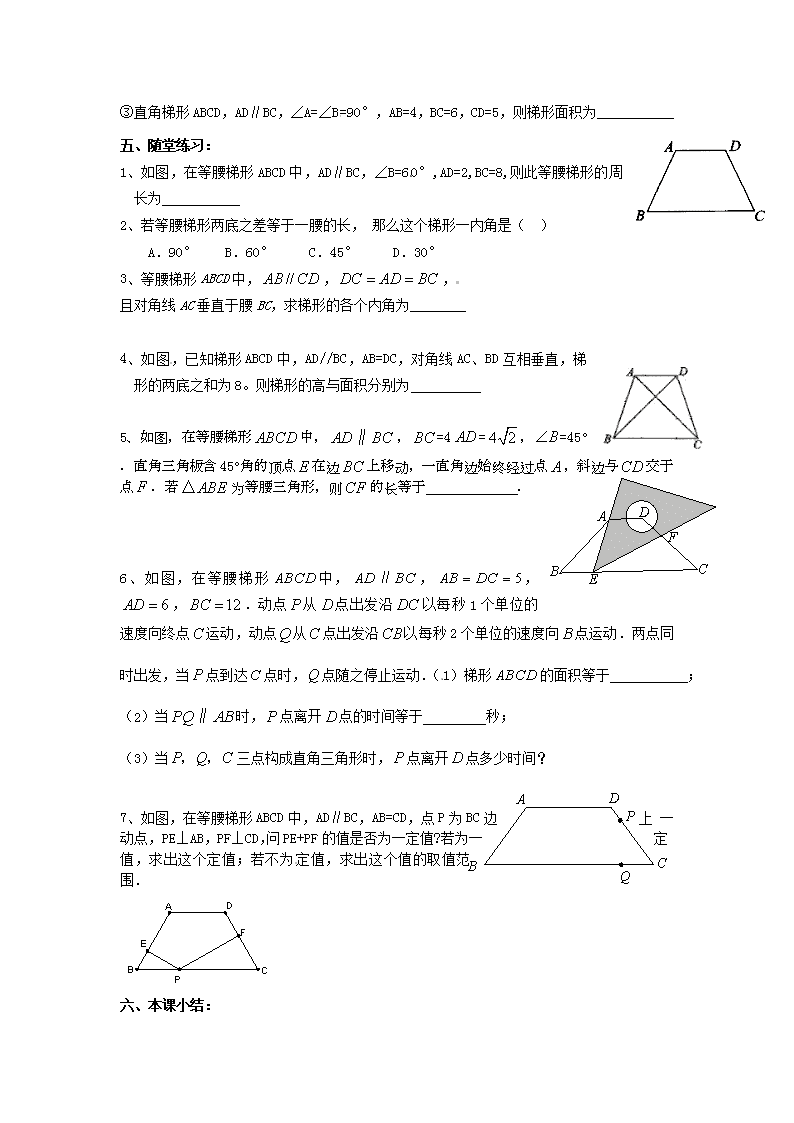
第20课时 梯形 ‎ ‎ 一、考试大纲要求：‎ ‎1、理解梯形、等腰梯形、直角梯形的概念。‎ ‎2、掌握等腰梯形的性质应用，以及辅助线的添加方法。‎ ‎3、理解并掌握等腰梯形的判定方法。‎ 二、重点、易错点分析：‎ 三、考题集锦：‎ ‎1、如图，梯形ABCD中，AB∥CD，AD = CD，E、F分别是AB、BC的中点，若∠1 = 35°，则∠D = ．‎ A D C B ‎2、如图，在直角梯形ABCD中，AB=‎4 cm,AD=‎5 cm,∠C=30°‎ 则DC= cm，BC= cm ‎3、梯形中，， ，，，， ‎ E C D A M N B 则的长为 ． ‎ ‎4、如图是小红设计的钻石形商标，△ABC是边长为2的等边三角形，四边形ACDE是等腰梯形，AC∥ED，∠EAC=60°，AE=1．‎ ‎（1）证明：△ABE≌△CBD； ‎ ‎（2）图中存在多对相似三角形，请你找出一对进行证明，并求出其相似比（不添加辅助线，不找全等的相似三角形）；‎ ‎（3）小红发现AM=MN=NC，请证明此结论；‎ 四、典型例题：‎ 考点一 一般梯形的性质 考点二 与梯形有关的计算 典例2、如图，已知梯形ABCD中，AD∥BC，∠B=30°，∠C=60°，AD=4，AB=，则下底BC的长为 __________．‎ 考点三 等腰梯形的性质 典例3、已知：如图，梯形ABCD中，DC∥AB，AD=BC，对角线AC、BD交于点O，∠COD=60°，若CD=3， AB=8，求梯形ABCD的高．‎ 考点四 等腰梯形的判定 典例4、如图，在梯形ABCD中，AB∥DC， DB平分∠ADC，过点A作AE∥BD，交CD的延长线于点E，且∠C＝2∠E．‎ E D C A B ‎（1）求证：梯形ABCD是等腰梯形．‎ ‎（2）若∠BDC＝30°，AD＝5，求CD的长．‎ 考点五、分类讨论专题 ‎①梯形一底为10，高为12，两腰分别为15和20，则梯形面积为 ‎ ‎②若等腰梯形ABCD的上、下底之和为4cm，并且两条对角线所夹锐角为60°，则该等腰梯形的面积为 ．‎ ‎③直角梯形ABCD，AD∥BC，∠A=∠B=90°，AB=4，BC=6，CD=5，则梯形面积为___________‎ 五、随堂练习：‎ ‎1、如图，在等腰梯形ABCD中，AD∥BC，∠B=60°,AD=2,BC=8,则此等腰梯形的周长为 ‎ ‎2、若等腰梯形两底之差等于一腰的长，那么这个梯形一内角是（ ）‎ ‎ A．90° B．60° C．45° D．30°‎ ‎3、等腰梯形ABCD中，，，‎ 且对角线AC垂直于腰BC，求梯形的各个内角为________‎ ‎4、如图，已知梯形ABCD中，AD//BC，AB=DC，对角线AC、BD互相垂直，梯形的两底之和为8。则梯形的高与面积分别为 ‎ D B C A E F ‎5、如图，在等腰梯形中，，=4=，=45°．直角三角板含45°角的顶点在边上移动，一直角边始终经过点，斜边与交于点．若为等腰三角形，则的长等于 ． ‎ ‎6、如图，在等腰梯形中，，，，．动点从点出发沿以每秒1个单位的速度向终点运动，动点从点出发沿以每秒2个单位的速度向点运动．两点同时出发，当点到达点时，点随之停止运动．（1）梯形的面积等于 ； （2）当时，点离开点的时间等于 秒；‎ A C Q D P B ‎（3）当三点构成直角三角形时，点离开点多少时间？‎ ‎7、如图，在等腰梯形ABCD中，AD∥BC，AB=CD，点P为BC边上一动点，PE⊥AB，PF⊥CD，问PE+PF的值是否为一定值?若为一定值，求出这个定值；若不为定值，求出这个值的取值范围．‎ 六、本课小结：‎