中考复习讲义2——方程与不等式
教学内容 方程与不等式
【中考回顾】
2011
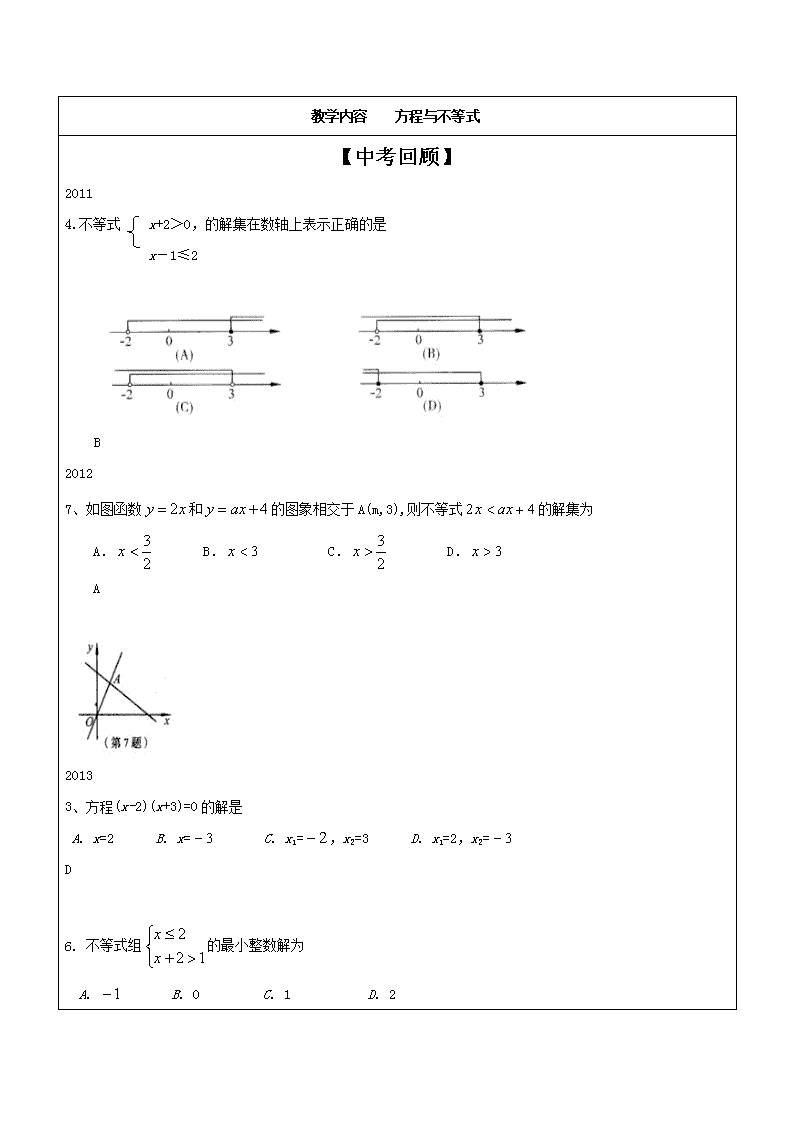
4.不等式 x+2>0,的解集在数轴上表示正确的是
x-1≤2
B
2012
7、如图函数和的图象相交于A(m,3),则不等式的解集为
A. B. C. D.
A
2013
3、方程(x-2)(x+3)=0的解是
A. x=2 B. x= C. x1=,x2=3 D. x1=2,x2=
D
6. 不等式组的最小整数解为
A. B. 0 C. 1 D. 2
B
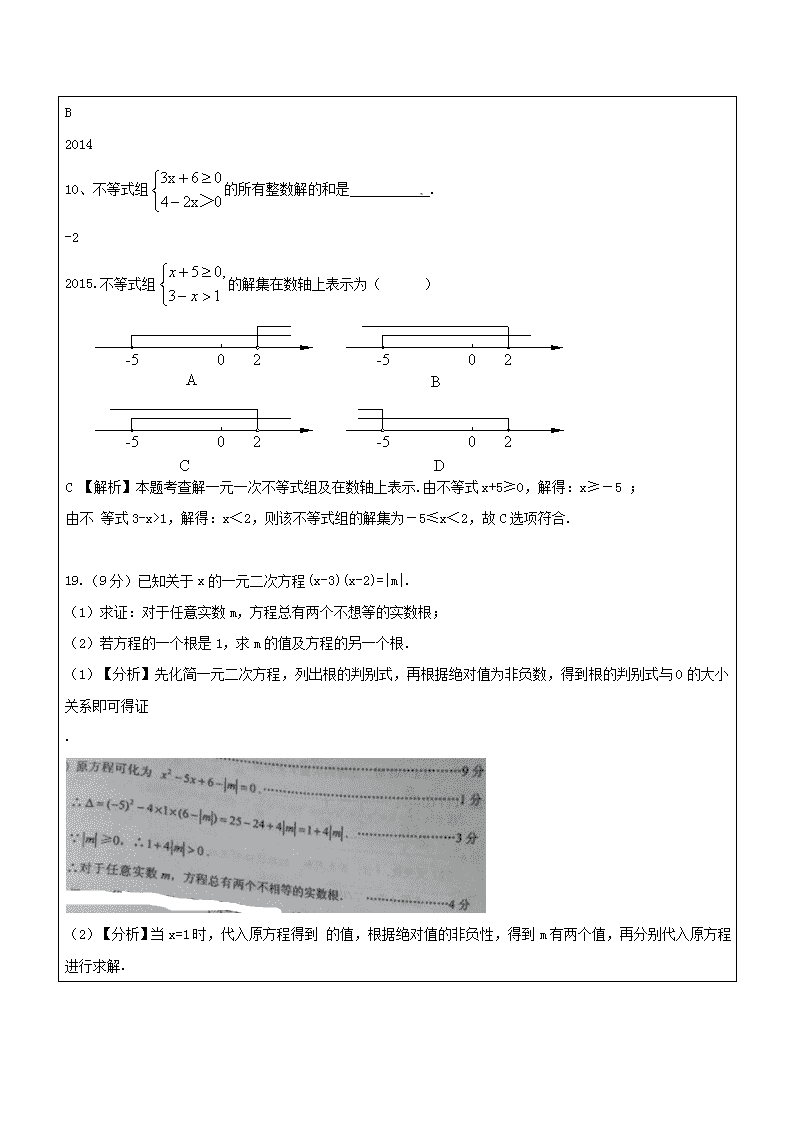
2014
10、不等式组的所有整数解的和是 .
-2
2015.不等式组的解集在数轴上表示为( )
-5
2
0
-5
2
0
-5
2
0
-5
2
0
C
D
B
A
C 【解析】本题考查解一元一次不等式组及在数轴上表示.由不等式x+5≥0,解得:x≥-5 ;
由不 等式3-x>1,解得:x<2,则该不等式组的解集为-5≤x<2,故C选项符合.
19.(9分)已知关于x的一元二次方程(x-3)(x-2)=|m|.
(1)求证:对于任意实数m,方程总有两个不想等的实数根;
(2)若方程的一个根是1,求m的值及方程的另一个根.
(1)【分析】先化简一元二次方程,列出根的判别式,再根据绝对值为非负数,得到根的判别式与0的大小关系即可得证
.
(2)【分析】当x=1时,代入原方程得到 的值,根据绝对值的非负性,得到m有两个值,再分别代入原方程进行求解.
【知识点梳理】
考点一、一元一次方程
1.方程
含有未知数的等式叫做方程.
2.方程的解
能使方程两边相等的未知数的值叫做方程的解.
3.等式的性质
(1)等式的两边都加上(或减去)同一个数或同一个整式,所得结果仍是等式.
(2)等式的两边都乘以(或除以)同一个数(除数不能是零),所得结果仍是等式.
4.一元一次方程
只含有一个未知数,并且未知数的最高次数是1的整式方程叫做一元一次方程,其中方程叫做一元一次方程的标准形式,a是未知数x的系数,b是常数项.
5.一元一次方程解法的一般步骤
整理方程 —— 去分母—— 去括号—— 移项—— 合并同类项——系数化为1——(检验方程的解).
解一元一次方程的一般步骤
步骤
名 称
方 法
依 据
注 意 事 项
1
去分母
在方程两边同时乘以所有分母的最小公倍数(即把每个含分母的部分和不含分母的部分都乘以所有分母的最小公倍数)
等式性质2
1、不含分母的项也要乘以最小公倍数;2、分子是多项式的一定要先用括号括起来.
2
去括号
去括号法则(可先分配再去括号)
乘法分配律
注意正确的去掉括号前带负数的括号
3
移项
等式性质1
移项一定要改变符号
把未知项移到方程的一边(左边),常数项移到另一边(右边)
4
合并 同类项
分别将未知项的系数相加、常数项相加
1、整式的加减;
2、有理数的加法法则
单独的一个未知数的系数为“±1”
5
系数化为“1”
在方程两边同时除以未知数的系数(或方程两边同时乘以未知数系数的倒数)
等式性质2
不要颠倒了被除数和除数(未知数的系数作除数——分母)
*6
检根
x=a
方法:把x=a分别代入原方程的两边,分别计算出结果.
① 若 左边=右边,则x=a是方程的解;
② 若 左边≠右边,则x=a不是方程的解.
注:当题目要求时,此步骤必须表达出来.
说明:
(1)上表仅说明了在解一元一次方程时经常用到的几个步骤,但并不是说,解每一个方程都必须经过六个步骤;
(2)解方程时,一定要先认真观察方程的形式,再选择步骤和方法;
(3)对于形式较复杂的方程,可依据有效的数学知识将其转化或变形成我们常见的形式,再依照一般方法解.
考点二、一元二次方程
1.一元二次方程
含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程.
2.一元二次方程的一般形式
,它的特征是:等式左边是一个关于未知数x的二次多项式,等式右边是零,其中叫做二次项,a叫做二次项系数;bx叫做一次项,b叫做一次项系数;c叫做常数项.
3.一元二次方程的解法
(1)直接开平方法
利用平方根的定义直接开平方求一元二次方程的解的方法叫做直接开平方法.直接开平方法适用于解形如的一元二次方程.根据平方根的定义可知,是b的平方根,当时,,,当b<0时,方程没有实数根.
开平方法步骤
适用无一次项的方程
(2)配方法
配方法是一种重要的数学方法,它不仅在解一元二次方程上有所应用,而且在数学的其他领域也有着广泛的应用.配方法的理论根据是完全平方公式,把公式中的a看做未知数x,并用x代替,则有.
配方法步骤 ①移项:左边只留二次项和一次项,右边为常数项 (移项要变号)
②同除:方程两边同除二次项系(每项都要除)
③配方:方程两边加上一次项系数一半的平方
④开平方:注意别忘根号和正负
⑤解方程:解两个一元一次方程
(3)公式法
公式法是用求根公式求一元二次方程的解的方法,它是解一元二次方程的一般方法.
一元二次方程的求根公式:
公式法步骤
① 将方程化为一般式
② 写出a、b、c
③ 求出,
④ 若b2-4ac<0,则原方程无实数解
⑤ 若b2-4ac>0,则原方程有两个不相等的实数根,代入公式求解
① 若b2-4ac=0,则原方程有两个相等的实数根,代入公式求解。
(4)因式分解法
因式分解法就是利用因式分解的手段,求出方程的解的方法,这种方法简单易行,是解一元二次方程最常用的方法.
因式分解法步骤 ①移项:使方程右边为0
②因式分解:将方程左边因式分解;
适用能因式分解的方程
方法:一提,二套,三十字,四分组
③由A∙B=0,则A=0或B=0,解两个一元一次方程
4.一元二次方程根的判别式
一元二次方程中,叫做一元二次方程的根的判别式,通常用“”来表示,即.
5.一元二次方程根与系数的关系
如果方程的两个实数根是,那么,.也就是说,对于任何一个有实数根的一元二次方程,两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商.
要点诠释:
一元二次方程的解法中直接开平方法和因式分解法是特殊方法,比较简单,但不是所有的一元二次方程都能用这两种方法去解,配方法和公式法是普通方法,一元二次方程都可以用这两种方法去解.
考点三、分式方程
1.分式方程
分母里含有未知数的方程叫做分式方程.
2.解分式方程的一般方法
解分式方程的思想是将“分式方程”转化为“整式方程”.它的一般解法是:
①去分母,方程两边都乘以最简公分母;
②解所得的整式方程;
③验根:将所得的根代入最简公分母,若等于零,就是增根,应该舍去;若不等于零,就是原方程的根.
3.分式方程的特殊解法
换元法:
换元法是中学数学中的一个重要的数学思想,其应用非常广泛,当分式方程具有某种特殊形式,一般的去分母不易解决时,可考虑用换元法.
要点诠释:
解分式方程时,求出未知数的值后必须验根,因为在把分式方程化为整式方程的过程中,扩大了未知数的取值范围,可能产生增根.
考点四、二元一次方程(组)
1.二元一次方程
含有两个未知数,并且未知项的最高次数是1的整式方程叫做二元一次方程,它的一般形式是
ax+by=c(a≠0,b≠0).
2.二元一次方程的解
使二元一次方程左右两边的值相等的一对未知数的值,叫做二元一次方程的一个解.
3.二元一次方程组
两个(或两个以上)二元一次方程合在一起,就组成了一个二元一次方程组.
4.二元一次方程组的解
使二元一次方程组的两个方程左右两边的值都相等的两个未知数的值,叫做二元一次方程组的解.
5.二元一次方程组的解法
①代入消元法;②加减消元法.
6.三元一次方程(组)
(1)三元一次方程
把含有三个未知数,并且含有未知数的项的次数都是1的整式方程叫三元一次方程.
(2)三元一次方程组
由三个(或三个以上)一次方程组成,并且含有三个未知数的方程组,叫做三元一次方程组.
要点诠释:
二元一次方程组的解法:
消元:将未知数的个数由多化少,逐一解决的想法,叫做消元思想.
(1)代入消元法:将一个未知数用含有另一个未知数的式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解,这种方法叫做代入消元法,简称代入法.
(2)加减消元法:当两个方程中同一未知数的系数相反或相等时,将两个方程的两边分别相加或相减,就能消去这个未知数,这种方法叫做加减消元法,简称加减法.
考点五、不等式(组)
1. 不等式的概念
(1)不等式
用不等号表示不等关系的式子,叫做不等式.
(2)不等式的解集
对于一个含有未知数的不等式,任何一个适合这个不等式的未知数的值,都叫做这个不等式的解.
对于一个含有未知数的不等式,它的所有解的集合叫做这个不等式的解的集合,简称这个不等式的解集.
求不等式的解集的过程,叫做解不等式.
2.不等式基本性质
性质1:不等式两边加上(或减去)同一个数(或式子),不等号的方向不变,即如a>b,那么a±c>b±c.
性质2:不等式两边乘以(或除以)同一个正数,不等号的方向不变,即如果a>b,c>0,那么ac>bc(或>).
性质3:不等式两边乘以(或除以)同一个负数,不等号的方向改变,即如果a>b,c<0,那么ac
).
不等式的其他性质:①若a>b,则bb,b>c,则a>c;③若a≥b,且b≥a,则a=b;④若a≤0,则a=0.
3.一元一次不等式
(1)一元一次不等式的概念
一般地,不等式中只含有一个未知数,未知数的次数是1,且不等式的两边都是整式,这样的不等式叫做一元一次不等式.
(2)一元一次不等式的解法
解一元一次不等式的一般步骤:
①去分母;②去括号;③移项;④合并同类项;⑤将x项的系数化为1.
4.一元一次不等式组
(1)一元一次不等式组的概念
几个一元一次不等式合在一起,就组成了一个一元一次不等式组.
几个一元一次不等式的解集的公共部分,叫做它们所组成的一元一次不等式组的解集.
求不等式组的解集的过程,叫做解不等式组.
当任何数x都不能使不等式同时成立,我们就说这个不等式组无解或其解为空集.
(2)一元一次不等式组的解法
①分别求出不等式组中各个不等式的解集;
②利用数轴求出这些不等式的解集的公共部分,即这个不等式组的解集.
要点诠释:
用符号“<”“>”“≤ ”“≥”“≠”表示不等关系的式子,叫做不等式.
由两个一元一次不等式组成的一元一次不等式组的解集的四种情况如下表.
不等式组
(其中a得:
把<3>代入<2>,得:
把代入<3>,得:
所以是原方程组的解。
解法二:加减消元法
将<1>两边同时乘以3,得:
由<2>-<3>,得:
把代入<1>,得:
所以是原方程组的解。
解法三:由<1>可得:
由<2>可得:
在同一个平面直角坐标系中作出一次函数和一次函数的图象,观察图象得交点为(-1,-4)。
所以方程组的解是
说明:
代入消元法解二元一次方程组的一般步骤:
(1)在方程组中选一个系数比较简单的方程,将这个方程变形成用含一个未知数的代数式表示另一个未知数的形式(一般称这个等式为关系式);
(2)将关系式代入另一个方程,消去一个未知数,得到一个一元一次方程;
(3)解这个一元一次方程求得一个未知数的值,再将它代入关系式,求得另一个未知数的值;
(4)把求得的未知数的值用联立符号表示出来。
加减消元法解二元一次方程组的一般步骤:
(1)使方程组中准备消掉的未知数在两个方程中的系数的绝对值相等;
(2)把两个方程的两边分别相加或相减,得到一个一元一次方程;
(3)解这个一元一次方程求得一个未知数的值,再将求得的未知数的值代入原方程组中的任意一个方程,求出另一个未知数的值;
(4)把求得的两个未知数的值按字母顺序用联立符号表示出来。
图象法的使用不如上面两种方法普遍,它只对交点的横、纵坐标都是整数值时适宜,其他情况下得进行估值。
【对应练习】
1、若关于x,y的二元一次方程组的解也是二元一次方程 的解,则k的值为 ( )
A. B. C. D.
2、已知是方程组的解,则a﹣b的值是( )
A. B. C. D.
3、解方程组:
类型五:不等式
【例1】
解不等式,并在数轴上表示它的解集
解:去分母,得
去括号,得
移项后,合并得
不等式两边同乘以11,得
它的解集在数轴上表示如图:
说明:一元一次不等式的解法与一元一次方程的解法相类似。应特别注意的是,当不等式的两边都乘以或除以同一个负数时,不等号的方向必须改变。本题可先去分母,此时不要漏乘,再去括号,然后化成或的形式,最后得出解集。
【例2】
.求不等式组的整数解
解:解不等式,得
解不等式,得
不等式组的解集为
其中整数解为-1,0,1,2
说明:不等式组的解集是组成不等式组的每一个不等式解集的公共部分,因此,解一元一次不等式是解一元一次不等式组的基础,会用数轴表示一元一次不等式的解集是正确求出一元一次不等式组解集的可靠保证。
【对应练习】
1、不等式组的解集是【 】
A. x>﹣1 B. x>2 C. ﹣1<x<2 D. x<2
2、(2014年江苏南通3分)若关于x的一元一次不等式组无解,则a的取值范围是【 】
A. B. C. D.
3、(2014年江苏徐州5分)解不等式组:.
4、(2014年江苏无锡4分)解不等式组:.
5、(2014年江苏连云港6分)解不等式,并把解集在数轴上表示出来.
6、不等式组的解集是
7、解不等式:并将它的解集在数轴上表示出来.
【课后作业】
一、选择题
1.点在第三象限,那么值是( )。
A. B. C. D.
2.不等式组的解集是x>,则的取值范围是( )。
A.≥3 B.=3 C.>3 D. <3
3.方程-1=的解是( )。
A.-1 B.2或-1 C.-2或3 D.3
4.方程- = 5的解是( )。
A. 5 B. - 5 C. 7 D.- 7
5.一元二次方程x2-2x-3=0的两个根分别为( )。
A.x1=1,x2=-3 B.x1=1,x2=3
C.x1=-1,x2=3 D.x1=-1,x2=-3
6.已知满足方程组则的值为( )。
A. B. C. D.
7. 若方程组的解与的和为0,则的值为( )。
A.-2 B.0 C.2 D.4
8.如果x1,x2是两个不相等实数,且满足x12-2x1=1,x22-2x2=1,
那么x1·x2等于( )。
A.2 B.-1 C.1 D.-2
9.在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形图.如果要使整个挂图的面积是5400cm2,设金色纸边的宽为xcm, 那么x满足的方程是( )。
A.x2+130x-1400=0 B.x2+65x-350=0
C.x2-130x-1400=0 D.x2-65x-350=0
10.若解分式方程-=产生增根,则m的值是( )。
A.-1或-2 B.-1或2 C.1或2 D.1或-2
二、填空题
11.不等式(m-2)x>2-m的解集为x<-1,则m的取值范围是__________________。
12.已知关于x的方程10x2-(m+3)x+m-7=0,若有一个根为0,则m=_________,这时方程的另一个根是_________。
13.不等式组的解集是x<m-2,则m的取值应为_________。
14.用换元法解方程,若设,则可得关于y的整式方程为___________________________。
三、解答题
15.解方程:
(1) (2x – 3)2 = (3x – 2)2
(2) 解方程:
16.解不等式组,并把其解集在数轴上表示出来:
四、(本题共2小题,每小题8分,满分16分)
17. 如图,8块相同的长方形地砖拼成一个长方形,每块长方形地砖的长和宽分别是多少?
18.某科技公司研制成功一种新产品,决定向银行贷款200万元资金用于生产这种产品,签定的合同约定两年到期时一次性还本付息,利息为本金的8%,该产品投放市场后,由于产销对路,使公司在两年到期时除还清贷款的本金和利息外,还盈余72万元;若该公司在生产期间每年比上一年资金增长的百分数相同,试求这个百分数。
五、(本题共2小题,每小题10分,满分20分)
19.将4个数a,b,c,d排成2行、2列,两边各加一条竖直线记成,定义 =ad-bc,上述记号就叫做2阶行列式.若=6,求x的值。
20.已知关于x,y的方程组与的解相同,求a,b的值。
六、(本题满分12 分)
21.小华在沿公路散步,往返公交车每隔分钟就有一辆迎面而过;每隔 分钟就有一辆从小华的背后而来.若小华与公交车均为匀速运动,求车站每隔几分钟发一班公交车?
七、(本题满分12分)
22.“十一”黄金周期间,某学校计划组织385名师生租车旅游,现知道出租公司有42座和60座两种客车,42座客车的租金每辆为320元,60座客车的租金每辆为460元。
(1)若学校单独租用这两种车辆各需多少钱?
(2)若学校同时租用这两种客车8辆(可以坐不满),而且要比单独租用一种车辆节省租金。请你帮助该学校选择一种最节省的租车方案。
八、(本题满分 14 分)
23.机械加工需要用油进行润滑以减少摩擦,某企业加工一台大型机械设备润滑用油量为90千克,用油的重复利用率为60%,按此计算,加工一台大型机械设备的实际耗油量为36千克.为了建设节约型社会,减少油耗,该企业的甲、乙两个车间都组织了人员为减少实际耗油量进行攻关.
(1)甲车间通过技术革新后,加工一台大型机械设备润滑油用油量下降到70千克,用油的重复利用率仍然为60%.问甲车间技术革新后,加工一台大型机械设备的实际耗油量是多少千克?
(2)乙车间通过技术革新后,不仅降低了润滑用油量,同时也提高了用油的重复利用率,并且发现在技术革新的基础上,润滑用油量每减少1千克,用油量的重复利用率将增加1.6%.这样乙车间加工一台大型机械设备的实际耗油量下降到12千克.问乙车间技术革新后,加工一台大型机械设备润滑用油量是多少千克?用油的重复利用率是多少?
中考数学总复习专题测试卷(三)参考答案
一、1、C 2、A 3、D 4、D 5、C 6、D 7、C 8、B
9、B 10、A
二、11、m<2; 12、7,1; 13、m≥-3; 14、。
三、15、(1)±1;
(2)去分母,得.
,解这个方程,得.
经检验,是原方程的解.
16.解:解不等式,得,
解不等式,得.
所以,原不等式组的解集是.在数轴上表示为
四、17. 每块长方形地砖的长是45cm,宽是15cm。
18.设每年增长的百分数为。
解得: (不合题意,舍去) 答:(略)
五、19.因为=ad-bc,所以=6可以转化为(x+1)(x+1)-(x-1)(1-x)=6,即(x+1)2+(x-1)2=6,所以x2=2,即x=±;
20. ,。
六、21.分钟.(提示:设车站每隔分钟发一班车,小华的速度为米/分,公交车的速度为米/分,则)
七、22.(1)385÷42≈9.2
∴单独租用42座客车需10辆,租金为320×10=3200元.
385÷60≈6.4
∴单独租用60座客车需7辆,租金为460×7=3220元.
(2)设租用42座客车 x 辆,则60座客车(8-x )辆,由题意得:
解之得:≤x≤.
∵x取整数, ∴x =4,5.
当x=4时,租金为320×4+460×(8-4)=3120元;
当x=5时,租金为320×5+460×(8-5)=2980元.
答:租用42座客车5辆,60座客车3辆时,租金最少。
说明:若学生列第二个不等式时将“≤”号写成“<”号,也对.
八、23.(1)由题意,得70×(1-60%)=70×40%=28(千克).
(2)设乙车间加工一台大型机械设备润滑用油量为x千克.
由题意,得:x×[1-(90-x)×1.6%-60%]=12,
整理得x2-65x-750=0,解得:x1=75,x2=-10(舍去),
(90-75)×1.6%+60%=84%.
答:(1)技术革新后,甲车间加工一台大型机械设备的实际耗油量是28千克.(2)技术革新后,乙车间加工一台大型机械设备润滑用油量是75千克,用油的重复利用率是84%.