九年级数学中考压轴题练习2及答案

九年级数学中考压轴题练习2及答案

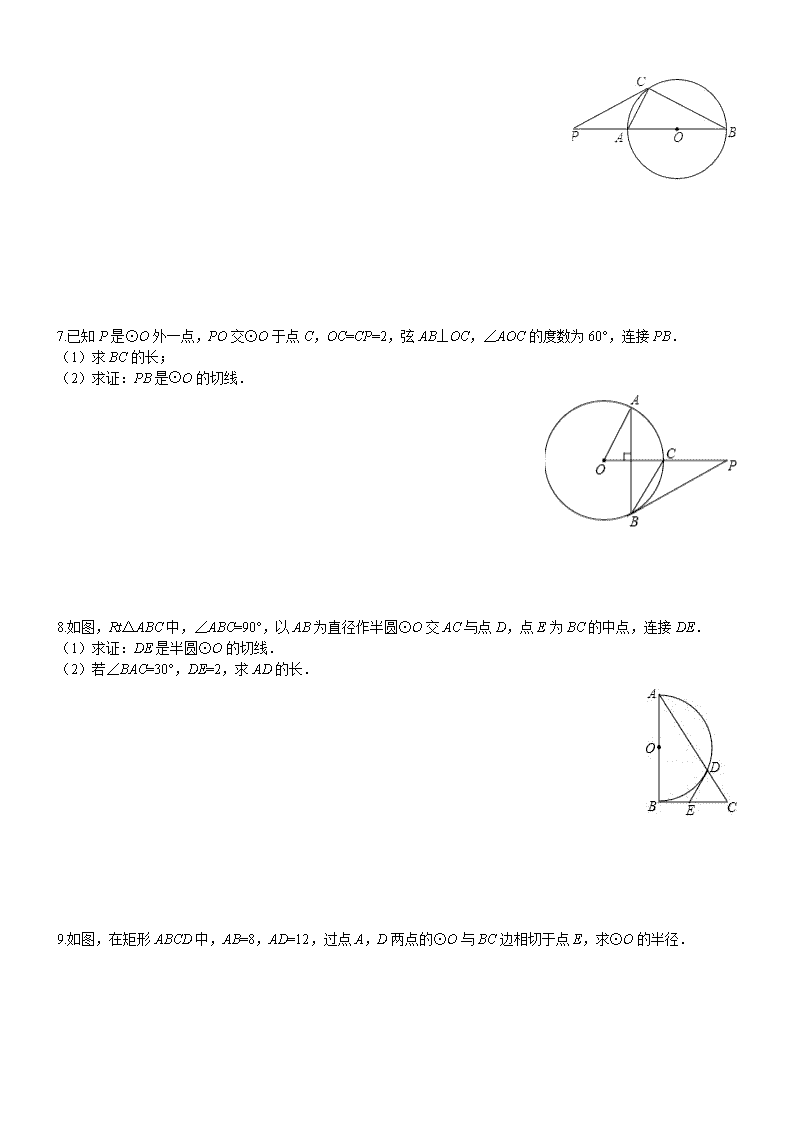
‎2017年九年级数学中考 综合题30题 如图,在△ABC中,以AB为直径的⊙O分别于BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F．‎ ‎（1）求证：DF⊥AC；‎ ‎（2）若⊙O的半径为5，∠CDF=30°，求的长（结果保留π）．‎ 如图，AB是⊙O的直径，∠BAC=90°，四边形EBOC是平行四边形，EB交⊙O于点D，连接CD并延长交AB的延长线于点F．‎ ‎（1）求证：CF是⊙O的切线；‎ ‎（2）若∠F=30°，EB=4，求图中阴影部分的面积（结果保留根号和π）‎ 如图，AB是⊙O的直径，AD是⊙O的弦，点F是DA延长线的一点，AC平分∠FAB交⊙O于点C，过点C作CE⊥DF，垂足为点E．‎ ‎（1）求证：CE是⊙O的切线；‎ ‎（2）若AE=1，CE=2，求⊙O的半径．‎ 如图，AB为⊙O的弦，若OA⊥OD,AB、OD相交于点C,且CD=BD.‎ ‎ （1）判定BD与⊙O的位置关系，并证明你的结论；‎ ‎ （2）当OA=3，OC=1时，求线段BD的长.‎ ‎ ‎ 如图，AB是⊙O的直径，弦CD⊥AB于点E，点P在⊙O上，∠1=∠BCD．‎ ‎（1）求证：CB∥PD；‎ ‎（2）若BC=3，sin∠BPD=0.6，求⊙O的直径．‎ ‎ ‎ 如图，已知AB是⊙的直径，AC是弦，点P是BA延长线上一点，连接PC，BC．∠PCA=∠B ‎（1）求证：PC是⊙O的切线；‎ ‎（2）若PC=6，PA=4，求直径AB的长．‎ 已知P是⊙O外一点，PO交⊙O于点C，OC=CP=2，弦AB⊥OC，∠AOC的度数为60°，连接PB．‎ ‎（1）求BC的长；‎ ‎（2）求证：PB是⊙O的切线．‎ ‎ ‎ 如图，Rt△ABC中，∠ABC=90°，以AB为直径作半圆⊙O交AC与点D，点E为BC的中点，连接DE．‎ ‎（1）求证：DE是半圆⊙O的切线．‎ ‎（2）若∠BAC=30°，DE=2，求AD的长．‎ 如图，在矩形ABCD中，AB=8，AD=12，过点A，D两点的⊙O与BC边相切于点E，求⊙O的半径．‎ 如图，在⊙O中，半径OA⊥OB，过点OA的中点C作FD∥OB交⊙O于D、F两点，且CD=，以O为圆心，OC为半径作，交OB于E点．‎ ‎（1）求⊙O的半径OA的长；‎ ‎（2）计算阴影部分的面积．‎ 如图，AB是以BC为直径的半圆O的切线，D为半圆上一点，AD=AB，AD，BC的延长线相交于点E．‎ ‎（1）求证：AD是半圆O的切线；‎ ‎（2）连结CD，求证：∠A=2∠CDE；‎ ‎（3）若∠CDE=27°，OB=2，求的长．‎ 如图，⊙O是△ABC的外接圆，圆心O在这个三角形的高AD上，AB=10，BC=12．‎ 求⊙O的半径.‎ 如图,⊙O的直径AB的长为10，弦AC的长为5，∠ACB的平分线交⊙O于点D.‎ ‎（1）求BC的长；（2）求弦BD的长.‎ ‎ ‎ 如图，⊙O的半径OD⊥弦AB于点C，连结AO并延长交⊙O于点E，连结EC．若AB=8，CD=2，求EC的长．‎ ‎ ‎ 如图，四边形ABCD内接于⊙O，点E在对角线AC上，EC=BC=DC ‎（1）若∠CBD=39°，求∠BAD的度数；‎ ‎（2）求证：∠1=∠2。‎ ‎ ‎ （1）如图1，将直角的顶点E放在正方形ABCD的对角线AC上，使角的一边交CD于点F，另一边交CB或其延长线于点G，求证：EF=EG；‎ ‎（2）如图2，将（1）中的“正方形ABCD”改成“矩形ABCD”，其他条件不变．若AB=m，BC=n，试求EF:EG的值；（3分）‎ ‎（3）如图3，将直角顶点E放在矩形ABCD的对角线交点，EF、EG分别交CD与CB于点F、G，且EC平分∠FEG．若AB=2，BC=4，求EG、EF 的长.‎ 将正方形ABCD放在如图所示的直角坐标系中,A点的坐标为(4,0),N点的坐标为(3,0)，MN平行于y轴，E是BC的中点，现将纸片折叠，使点C落在MN上，折痕为直线EF.‎ ‎(1)求点G的坐标；‎ ‎(2)求直线EF的解析式；‎ ‎(3)设点P为直线EF上一点，是否存在这样的点P，使以P, F, G的三角形是等腰三角形?若存在，直接写出P 点的坐标;若不存在，请说明理由.‎ 如图，在矩形ABCD中，B (16, 12)，E, F分别是OC, BC上的动点，EC+CF=8.‎ ‎(1)当∠AFB=600时，△ABF沿着直线AF折叠，折叠后，落在平面内G点处，求G点的坐标.‎ ‎(2)当F运动到什么位置时，△AEF的面积最小，最小为多少?‎ ‎(3)当△AEF的面积最小时，直线EF与y轴相交于点M, P点在x轴上，OP与直线EF相切于点M，求P点的坐标.‎ ‎ ‎ 如图,在Rt△ABC中,∠B=90°,AC=‎60cm,∠A=60°,点D从点C出发沿CA方向以‎4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以‎2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒（0＜t≤15）.过点D作DF⊥BC于点F,连接DE，EF．‎ ‎（1）求证：AE=DF；‎ ‎（2）四边形AEFD能够成为菱形吗？如果能,求出相应的t值，如果不能，说明理由；‎ ‎（3）当t为何值时,△DEF为直角三角形？请说明理由．‎ 已知,四边形ABCD是正方形，∠MAN= 45º，它的两边，边AM、AN分别交CB、DC与点M、N，连接MN，作AH⊥MN，垂足为点H ‎ （1）如图1，猜想AH与AB有什么数量关系？并证明；‎ ‎ （2）如图2，已知∠BAC =45º，AD⊥BC于点D，且BD=2，CD=3，求AD的长．‎ ‎ 小萍同学通过观察图①发现，△ABM和△AHM关于AM对称，△AHN和△ADN关于AN对称，于是她巧妙运用这个发现，将图形如图③进行翻折变换，解答了此题。你能根据小萍同学的思路解决这个问题吗？‎ ‎ ‎ 两块等腰直角三角形纸片AOB和COD按图1所示放置，直角顶点重合在点O处，AB=25，CD=17．保持纸片AOB不动，将纸片COD绕点O逆时针旋转α（0°<α<90°）角度，如图2所示．‎ ‎（1）利用图2证明AC=BD且AC⊥BD；‎ ‎（2）当BD与CD在同一直线上（如图3）时，求AC的长和α的正弦值．‎ 如图,抛物线y=ax2+bx-5(a≠0)经过点A(4,-5)，与x轴的负半轴交于点B，与y轴交于点C，且OC=5OB，抛物线的顶点为D；‎ ‎（1）求这条抛物线的表达式；‎ ‎（2）联结AB、BC、CD、DA，求四边形ABCD的面积；‎ ‎（3）如果点E在y轴的正半轴上，且∠BEO=∠ABC，求点E的坐标；‎ ‎ ‎ 在平面直角坐标系xOy中，抛物线y=ax2+bx+2过B（﹣2，6），C（2，2）两点．‎ ‎（1）试求抛物线的解析式；‎ ‎（2）记抛物线顶点为D，求△BCD的面积；‎ ‎（3）若直线y=﹣0.5x向上平移b个单位所得的直线与抛物线段BDC（包括端点B、C）部分有两个交点，求b的取值范围．‎ 如图,已知一次函数y=0.5x+1的图象与x轴交于点A，与y轴交于点B；二次函数y=0.5x2+bx+c的图象与一次函数y=0.5x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1，0)．‎ ‎（1）求二次函数的解析式；‎ ‎（2）求四边形BDEC的面积S；‎ ‎（3）在x轴上是否存在点P,使得△PBC是以P为直角顶点的直角三角形？若存在，求出所有的点P，若不存在，请说明理由．‎ 已知抛物线y=ax2+bx+c与x轴交于A(-1，0),B(5，0),与y轴交于C(0，3).直线y=x+1与抛物线交于A、E两点，与抛物线对称轴交于点D.‎ ‎ (1)求抛物线解析式及E点坐标；‎ ‎ (2)在对称轴上是否存在一点M，使ACM为等腰三角形？若存在，请直接写出M点坐标；若不存在，请说明理由.‎ ‎ (3)若一点P在直线y=x+1上从A点出发向AE方向运动，速度为单位/秒，过P点作PQ//y轴，交抛物线于 Q点.设时间为t秒(0≤t≤6)，PQ的长度为L，找出L与t的函数关系式，并求出PQ最大值.‎ ‎ ‎ 如图，已知在平面直角坐标系中，点A（4，0）是抛物线y=ax2+2x﹣c上的一点，将此抛物线向下平移6个单位后经过点B（0，2），平移后所得的新抛物线的顶点记为C，新抛物线的对称轴与线段AB的交点记为P．‎ ‎（1）求平移后所得到的新抛物线的表达式，并写出点C的坐标；‎ ‎（2）求∠CAB的正切值；‎ ‎（3）如果点Q是新抛物线对称轴上的一点，且△BCQ与△ACP相似，求点Q的坐标．‎ ‎ ‎ 如图，已知抛物线与x轴交于A（﹣1，0）、B（5，0）两点，与y轴交于点C（0，5）．‎ ‎（1）求该抛物线所对应的函数关系式；‎ ‎（2）D是笫一象限内抛物线上的一个动点（与点C、B不重合），过点D作DF⊥x轴于点F，交直线BC于点E，连结BD、CD．设点D的横坐标为m，△BCD的面积为S．‎ ‎①求S关于m的函数关系式及自变量m的取值范围；‎ ‎②当m为何值时，S有最大值，并求这个最大值；‎ ‎③直线BC能否把△BDF分成面积之比为2：3的两部分？若能，请求出点D的坐标；若不能，请说明理由．‎ ‎ ‎ 对于某一函数给出如下定义：若存在实数p，当其自变量的值为p时，其函数值等于p,则称p为这个函数的不变值.在函数存在不变值时,该函数的最大不变值与最小不变值之差q称为这个函数的不变长度.特别地,当函数只有一个不变值时,其不变长度q为零.例如：下图中的函数有0,1两个不变值,其不变长度q等于1.‎ ‎ (1)分别判断函数y=x-1，y=x-1,y=x2有没有不变值？如果有，直接写出其不变长度；‎ ‎ (2)函数y=2x2-bx.‎ ‎ ①若其不变长度为零，求b的值；‎ ‎ ②若1≤b≤3,求其不变长度q的取值范围；‎ ‎ (3) 记函数y=x2-2x(x≥m)的图象为G1，将G1沿x=m翻折后得到的函数图象记为G2，函数G的图象由G1和G2两部分组成，若其不变长度q满足0≤q≤3,则m的取值范围为 .‎ ‎ ‎ 如图,直线y=0.5x与抛物线y=ax2＋b(a≠0)交于点A(-4,-2)和B(6,3),抛物线与y轴的交点为C．‎ ‎(1)求这个抛物线的解析式；‎ ‎(2)在抛物线上存在点M，使△MAB是以AB为底边的等腰三角形，求点M的坐标；‎ ‎(3)在抛物线上是否存在点P，使得△PAC的面积是△ABC的面积的四分之三？若存在，求出此时点P的坐标；若不存在，请说明理由．‎ 如图，在平面直角坐标系中，已知抛物线y=x2+bx+c过A，B，C三点，点A的坐标是(3,0)，点C的坐标是(0,-3)，动点P在抛物线上．‎ ‎（1）b =_________，c =_________，点B的坐标为_____________；（直接填写结果）‎ ‎（2）是否存在点P，使得△ACP是以AC为直角边的直角三角形？若存在，求出所有符合条件 的点P的坐标；若不存在，说明理由；‎ ‎（3）过动点P作PE垂直y轴于点E，交直线AC于点D，过点D作x轴的垂线．垂足为F，连 接EF，当线段EF的长度最短时，求出点P的坐标．‎ 参考答案 ‎1.（1）证明：连接OD，如图所示．‎ ‎∵DF是⊙O的切线，D为切点，∴OD⊥DF，∴∠ODF=90°．‎ ‎∵BD=CD，OA=OB，∴OD是△ABC的中位线，∴OD∥AC，‎ ‎∴∠CFD=∠ODF=90°，∴DF⊥AC．‎ ‎（2）解：∵∠CDF=30°，由（1）得∠ODF=90°，∴∠ODB=180°﹣∠CDF﹣∠ODF=60°．‎ ‎∵OB=OD，∴△OBD是等边三角形，∴∠BOD=60°，∴的长===π．‎ ‎2.（1）证明：如图连接OD．‎ ‎∵四边形OBEC是平行四边形，∴OC∥BE，∴∠AOC=∠OBE，∠COD=∠ODB，‎ ‎∵OB=OD，∴∠OBD=∠ODB，∴∠DOC=∠AOC，‎ 在△COD和△COA中，，∴△COD≌△COA，‎ ‎∴∠CAO=∠CDO=90°，∴CF⊥OD，∴CF是⊙O的切线．‎ ‎（2）解：∵∠F=30°，∠ODF=90°，∴∠DOF=∠AOC=∠COD=60°，‎ ‎∵OD=OB，∴△OBD是等边三角形，∴∠DBO=60°，‎ ‎∵∠DBO=∠F+∠FDB，∴∠FDB=∠EDC=30°，‎ ‎∵EC∥OB，∴∠E=180°﹣∠OBD=120°，‎ ‎∴∠ECD=180°﹣∠E﹣∠EDC=30°，∴EC=ED=BO=DB，∵EB=4，∴OB=OD═OA=2，‎ 在RT△AOC中，∵∠OAC=90°，OA=2，∠AOC=60°，∴AC=OA•tan60°=2，‎ ‎∴S阴=2•S△AOC﹣S扇形OAD=2××2×2﹣=2﹣．‎ ‎3.（1）证明：连接CO，‎ ‎∵OA=OC，∴∠OCA=∠OAC，‎ ‎∵AC平分∠FAB，∴∠OCA=∠CAE，∴OC∥FD，‎ ‎∵CE⊥DF，∴OC⊥CE，∴CE是⊙O的切线；‎ ‎（2）证明：连接BC，在Rt△ACE中，AC===，‎ ‎∵AB是⊙O的直径，∴∠BCA=90°，∴∠BCA=∠CEA，‎ ‎∵∠CAE=∠CAB，∴△ABC∽△ACE，∴=，∴，‎ ‎∴AB=5，∴AO=2.5，即⊙O的半径为2.5．‎ ‎4.证明：连接OB，‎ ‎∵OA=OB，CD=DB，∴∠OAC=∠OBC，∠DCB=∠DBC．‎ ‎∵∠OAC+∠ACO=90°，∠ACO=∠DCB，∴∠OBC+∠DBC=90°．‎ ‎∴OB⊥BD．即BD是⊙O的切线．‎ ‎ （2）BD=4.‎ ‎5.（1）证明：∵∠D=∠1，∠1=∠BCD，∴∠D=∠BCD，∴CB∥PD；‎ ‎（2）解：连接AC，∵AB是⊙O的直径，∴∠ACB=90°，‎ ‎∵CD⊥AB，∴弧BD=弧BC，∴∠BPD=∠CAB，‎ ‎∴sin∠CAB=sin∠BPD=，即=，∵BC=3，∴AB=5，即⊙O的直径是5．‎ ‎6.（1）证明：连接OC，如图所示：‎ ‎∵AB是⊙的直径，∴∠ACB=90°，即∠1+∠2=90°，‎ ‎∵OB=OC，∴∠2=∠B，又∵∠PCA=∠B，∴∠PCA=∠2，‎ ‎∴∠1+∠PCA=90°，即PC⊥OC，∴PC是⊙O的切线；‎ ‎（2）解：∵PC是⊙O的切线，∴PC2=PA•PB，‎ ‎∴62=4×PB，解得：PB=9，∴AB=PB﹣PA=9﹣4=5．‎ ‎7.（1）解：如图，连接OB．‎ ‎∵AB⊥OC，∠AOC=60°，∴∠OAB=30°，‎ ‎∵OB=OA，∴∠OBA=∠OAB=30°，∴∠BOC=60°，‎ ‎∵OB=OC，∴△OBC的等边三角形，∴BC=OC．又OC=2，∴BC=2；‎ ‎（2）证明：由（1）知，△OBC的等边三角形，则∠COB=60°，BC=OC．‎ ‎∵OC=CP，∴BC=PC，∴∠P=∠CBP．‎ 又∵∠OCB=60°，∠OCB=2∠P，∴∠P=30°，∴∠OBP=90°，即OB⊥PB．‎ 又∵OB是半径，∴PB是⊙O的切线．‎ ‎8.1）证明：连接OD，OE，BD，‎ ‎∵AB为圆O的直径，∴∠ADB=∠BDC=90°，‎ 在Rt△BDC中，E为斜边BC的中点，∴DE=BE，‎ 在△OBE和△ODE中，，∴△OBE≌△ODE（SSS），‎ ‎∴∠ODE=∠ABC=90°，则DE为圆O的切线；‎ ‎（2）在Rt△ABC中，∠BAC=30°，∴BC=AC，‎ ‎∵BC=2DE=4，∴AC=8，‎ 又∵∠C=60°，DE=CE，‎ ‎∴△DEC为等边三角形，即DC=DE=2，则AD=AC﹣DC=6．‎ ‎9.解：连接OE，并反向延长交AD于点F，连接OA，‎ ‎∵BC是切线，∴OE⊥BC，∴∠OEC=90°，‎ ‎∵四边形ABCD是矩形，∴∠C=∠D=90°，∴四边形CDFE是矩形，‎ ‎∴EF=CD=AB=8，OF⊥AD，∴AF=AD=×12=6，‎ 设⊙O的半径为x，则OE=EF﹣OE=8﹣x，‎ 在Rt△OAF中，OF2+AF2=OA2，则（8﹣x）2+36=x2，‎ 解得：x=6.25，∴⊙O的半径为：6.25．‎ ‎10.解；（1）连接OD，‎ ‎∵OA⊥OB，∴∠AOB=90°，∵CD∥OB，∴∠OCD=90°，‎ 在RT△OCD中，∵C是AO中点，CD=，∴OD=2CO，设OC=x，‎ ‎∴x2+（）2=（2x）2，∴x=1，∴OD=2，∴⊙O的半径为2．‎ ‎（2）∵sin∠CDO==，∴∠CDO=30°，‎ ‎∵FD∥OB，∴∠DOB=∠ODC=30°，‎ ‎∴S圆=S△CDO+S扇形OBD﹣S扇形OCE=×+﹣=+．‎ ‎11.（1）证明：连接OD，BD，‎ ‎∵AB是⊙O的直径，∴AB⊥BC，即∠ABO=90°，∵AB=AD，∴∠ABD=∠ADB，‎ ‎∵OB=OD，∴∠DBO=∠BDO，∴∠ABD+∠DBO=∠ADB+∠BDO，‎ ‎∴∠ADO=∠ABO=90°，∴AD是半圆O的切线；‎ ‎（2）证明：由（1）知，∠ADO=∠ABO=90°，‎ ‎∴∠A=360°﹣∠ADO﹣∠ABO﹣∠BOD=180°﹣∠BOD，‎ ‎∵AD是半圆O的切线，∴∠ODE=90°，∴∠ODC+∠CDE=90°，‎ ‎∵BC是⊙O的直径，∴∠ODC+∠BDO=90°，∴∠BDO=∠CDE，‎ ‎∵∠BDO=∠OBD，∴∠DOC=2∠BDO，∴∠DOC=2∠CDE，∴∠A=∠CDE；‎ ‎（3）解：∵∠CDE=27°，∴∠DOC=2∠CDE=54°，∴∠BOD=180°﹣54°=126°，‎ ‎∵OB=2，∴的长==π．‎ ‎12.答案：6.25.‎ ‎13.（1）；（2）.‎ ‎14.‎ ‎15.‎ ‎16.‎ ‎17.‎ ‎18.略 ‎19.解：（1）证明：∵直角△ABC中，∠C=90°﹣∠A=30°．‎ ‎∵CD=4t，AE=2t，又∵在直角△CDF中，∠C=30°，∴DF=0.5CD=2t，∴DF=AE；‎ 解：（2）∵DF∥AB，DF=AE，∴四边形AEFD是平行四边形，‎ 当AD=AE时，四边形AEFD是菱形，即60﹣4t=2t，解得：t=10，即当t=10时，▱AEFD是菱形；‎ ‎（3）当t=7.5时△DEF是直角三角形（∠EDF=90°）；‎ 当t=12时，△DEF是直角三角形（∠DEF=90°）．理由如下：‎ 当∠EDF=90°时，DE∥BC．∴∠ADE=∠C=30°∴AD=2AE ‎∵CD=4t，∴DF=2t=AE，∴AD=4t，∴4t+4t=60，∴t=7.5时，∠EDF=90°．‎ 当∠DEF=90°时，DE⊥EF，∵四边形AEFD是平行四边形，∴AD∥EF，∴DE⊥AD，‎ ‎∴△ADE是直角三角形，∠ADE=90°，∵∠A=60°，∴∠DEA=30°，∴AD=0.5AE，‎ AD=AC﹣CD=60﹣4t，AE=DF=0.5CD=2t，∴60﹣4t=t，解得t=12．‎ 综上所述，当t=7.5时△DEF是直角三角形（∠EDF=90°）；当t=12时，△DEF是直角三角形（∠DEF=90°）．‎ ‎20.（1）答：AB=AH. 证明：延长CB至E使BE=DN，连结AE ‎∵四边形ABCD是正方形，∴∠ABC=∠D=90°，∴∠ABE=180°－∠ABC=90°‎ 又∵AB=AD∴△ABE≌△AEN（SAS）∴∠1=∠2，AE=AN ‎∵∠BAD=90°，∠MAN=45°∴∠1+∠3=90°－∠MAN＝45°∴∠2+∠3=45°即∠EAM=45°‎ 又AM=AM∴△EAM≌△NAM（SAS）‎ 又EM和NM是对应边∴AB=AH（全等三角形对应边上的高相等）‎ ‎(2)作△ABD关于直线AB的对称△ABE，作△ACD关于直线AC的对称△ACF， ‎ ‎∵AD是△ABC的高，∴∠ADB=∠ADC=90°∴∠E=∠F=90°，‎ 又∠BAC=45°∴∠EAF=90°延长EB、FC交于点G，则四边形AEGF是矩形，‎ 又AE=AD=AF∴四边形AEGF是正方形 由（1）、（2）知：EB=DB=2，FC=DC=3设AD=x，则EG=AE=AD=FG=x ‎∴BG=x－2；CG=x－3；BC=2+3=5在Rt△BGC中，(x-2)2+(x-3)2=52‎ 解之 得x1=6,x2=-1（舍去）∴AD的长为6.‎ ‎21.（1）证明：如图2中，延长BD交OA于G，交AC于E．‎ ‎∵∠AOB=∠COD=90°，∴∠AOC=∠DOB，‎ 在△AOC和△BOD中，，∴△AOC≌△BOD，∴AC=BD，∠CAO=∠DBO，‎ ‎∵∠DBO+∠GOB=90°，∵∠OGB=∠AGE，∴∠CAO+∠AGE=90°，∴∠AEG=90°，∴BD⊥AC．‎ ‎（2）解：如图3中，设AC=x，∵BD、CD在同一直线上，BD⊥AC，∴△ABC是直角三角形，‎ ‎∴AC2+BC2=AB2，∴x2+（x+17）2=252，解得x=7，‎ ‎∵∠ODC=∠α+∠DBO=45°,∠ABC+∠DBO=45°,∴∠α=∠ABC，‎ ‎∴sinα=sin∠ABC==．‎ ‎22.‎ ‎23.‎ ‎ ‎ ‎24.‎ ‎25.解：(1)y=-0.6x2+2.4x+3,E(10/3,13/3)；‎ ‎ (2)M(2，-1),(2，1),(2，3+),(2，3-)；‎ ‎ (3)L=-0.6t2+1.4t+2(0≤t≤10/3)；L=0.6t2-1.4t-4(10/3

查看更多