中考数学压轴题填空选择解答题分类汇编二及答案
2012填空压轴、选择压轴、压轴题、倒数第二题(2:H)
海南省14.星期6,小亮从家里骑自行车到同学家去玩,然后返回,图是他离家的路程y(千米)与时间x(分钟)的函数图象。下列说法不一定正确的是【 】
A.小亮家到同学家的路程是3千米 B.小亮在同学家返回的时间是1小时
C.小亮去时走上坡路,回家时走下坡路 D.小亮回家时用的时间比去时用的时间少
【分析】从函数的图象可知,小亮家到同学家的路程是3千米;小亮在同学家返回的时间是80-20=60(分钟)=1小时;小亮回家时用的时间为95-80=15(分钟),去时用的时间为20分钟,所以小亮回家时用的时间比去时用的时间少。故选项A,B,D都正确。对于选项B,虽然小亮回家时用的时间比去时用的时间少,这只能说明小亮回家时骑自行车的速度加快了,而不一定就是小亮去时走上坡路,回家时走下坡路。
故选C。
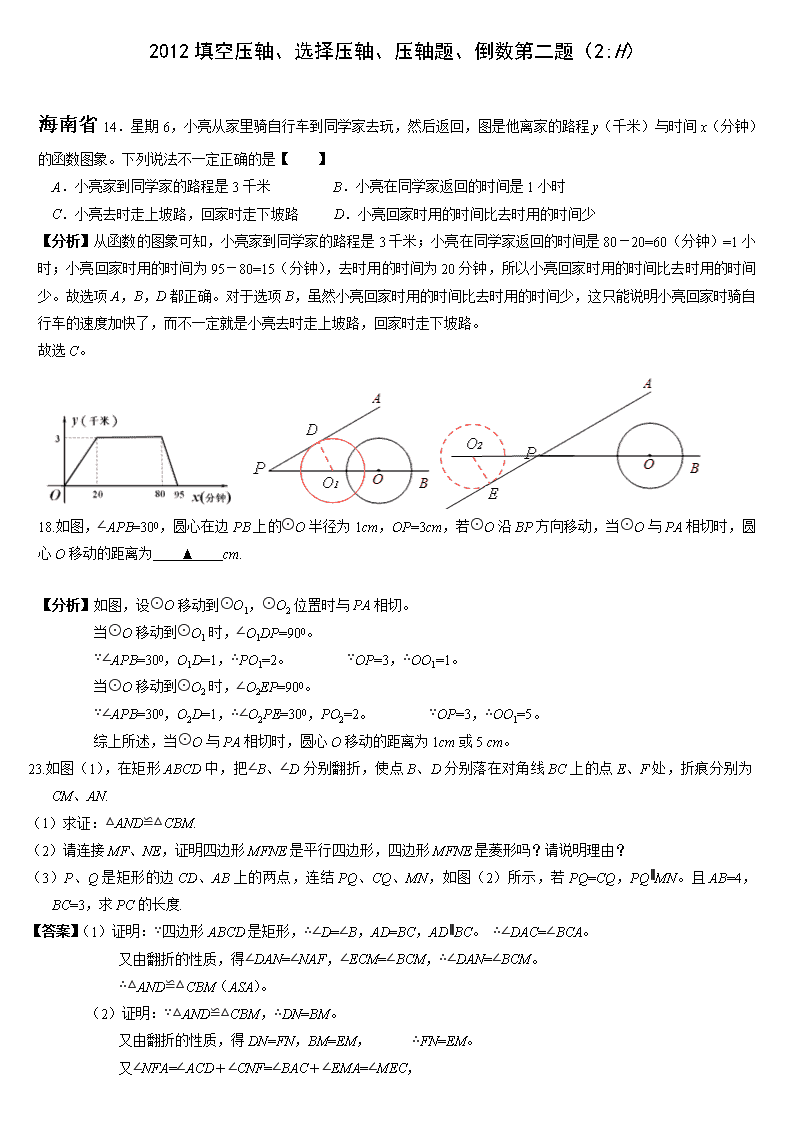
18.如图,∠APB=300,圆心在边PB上的⊙O半径为1cm,OP=3cm,若⊙O沿BP方向移动,当⊙O与PA相切时,圆心O移动的距离为 ▲ cm.
【分析】如图,设⊙O移动到⊙O1,⊙O2位置时与PA相切。
当⊙O移动到⊙O1时,∠O1DP=900。
∵∠APB=300,O1D=1,∴PO1=2。 ∵OP=3,∴OO1=1。
当⊙O移动到⊙O2时,∠O2EP=900。
∵∠APB=300,O2D=1,∴∠O2PE=300,PO2=2。 ∵OP=3,∴OO1=5。
综上所述,当⊙O与PA相切时,圆心O移动的距离为1cm或5 cm。
23.如图(1),在矩形ABCD中,把∠B、∠D分别翻折,使点B、D分别落在对角线BC上的点E、F处,折痕分别为CM、AN.
(1)求证:△AND≌△CBM.
(2)请连接MF、NE,证明四边形MFNE是平行四边形,四边形MFNE是菱形吗?请说明理由?
(3)P、Q是矩形的边CD、AB上的两点,连结PQ、CQ、MN,如图(2)所示,若PQ=CQ,PQ∥MN。且AB=4,BC=3,求PC的长度.
【答案】(1)证明:∵四边形ABCD是矩形,∴∠D=∠B,AD=BC,AD∥BC。 ∴∠DAC=∠BCA。
又由翻折的性质,得∠DAN=∠NAF,∠ECM=∠BCM,∴∠DAN=∠BCM。
∴△AND≌△CBM(ASA)。
(2)证明:∵△AND≌△CBM,∴DN=BM。
又由翻折的性质,得DN=FN,BM=EM, ∴FN=EM。
又∠NFA=∠ACD+∠CNF=∠BAC+∠EMA=∠MEC,
∴FN∥EM。∴四边形MFNE是平行四边形。
四边形MFNE不是菱形,理由如下:由翻折的性质,得∠CEM=∠B=900,
∴在△EMF中,∠FEM>∠EFM。∴FM>EM。∴四边形MFNE不是菱形。
(3)解:∵AB=4,BC=3,∴AC=5。
设DN=x,则由S△ADC=S△AND+S△NAC得3 x+5 x=12,解得x=,
即DN=BM=。
过点N作NH⊥AB于H,则HM=4-3=1。
在△NHM中,NH=3,HM=1,由勾股定理,得NM=。
∵PQ∥MN,DC∥AB,
∴四边形NMQP是平行四边形。∴NP=MQ,PQ= NM=。
又∵PQ=CQ,∴CQ=。
在△CBQ中,CQ=,CB=3,由勾股定理,得BQ=1。
∴NP=MQ=。∴PC=4--=2。
24.如图,顶点为P(4,-4)的二次函数图象经过原点(0,0),点A在该图象上,
OA交其对称轴于点M,点M、N关于点P对称,连接AN、ON
(1)求该二次函数的关系式.
(2)若点A的坐标是(6,-3),求△ANO的面积.
(3)当点A在对称轴右侧的二次函数图象上运动,请解答下列问题:
①证明:∠ANM=∠ONM
②△ANO能否为直角三角形?如果能,请求出所有符合条件的点A的坐标,如果不能,请说明理由.
【答案】解:(1)∵二次函数图象的顶点为P(4,-4),∴设二次函数的关系式为。
又∵二次函数图象经过原点(0,0),∴,解得。
∴二次函数的关系式为,即。
(2)设直线OA的解析式为,将A(6,-3)代入得,解得。
∴直线OA的解析式为。
把代入得。∴M(4,-2)。
又∵点M、N关于点P对称,∴N(4,-6),MN=4。
∴。
(3)①证明:过点A作AH⊥于点H,,与x轴交于点D。则
设A(),
则直线OA的解析式为。
则M(),N(),H()。
∴OD=4,ND=,HA=,NH=。
∴。
∴。∴∠ANM=∠ONM。
②不能。理由如下:分三种情况讨论:
情况1,若∠ONA是直角,由①,得∠ANM=∠ONM=450,
∴△AHN是等腰直角三角形。∴HA=NH,即。
整理,得,解得。
∴此时,点A与点P重合。故此时不存在点A,使∠ONA是直角。
情况2,若∠AON是直角,则。
∵ ,
∴。
整理,得,解得,。
∴此时,故点A与原点或与点P重合。故此时不存在点A,使∠AON是直角。
情况3,若∠NAO是直角,则△AMN∽△DMO∽△DON,∴。
∵OD=4,MD=,ND=,∴。
整理,得,解得。
∴此时,点A与点P重合。故此时不存在点A,使∠ONA是直角。
综上所述,当点A在对称轴右侧的二次函数图象上运动时,△ANO不能成为直角三角形。
河北12.如图6,抛物线与交于点,过点作轴的平行线,分别交两条抛物线于点.则以下结论:
①无论取何值,的值总是正数.②.
③当时,.④.
其中正确结论是( )
(1) ①② B.②③ C.③④ D.①④
解:开口向上,且与轴无交点,所以无论取何值,的值总是正数,即①是正确的,从而排除B、C.
又,点是、的交点,即点在上,从而排除A,故选D.
18.用4个全等的正八边形进行拼接,使相邻的两个正八边形有一条公共边,围成一圈后中间形成一个正方形,如图,用个全等的正六边形按这种方式拼接,如图,若围成一圈后中间也形成一个正多边形,则的值为 .
解:验证图9-1,正八边形的一个内角,围成一圈后中间形成的正多边形的一个内角,,所以用4个全等的正八边形进行拼接,使相邻的两个正八边形有一条公共边,围成一圈后中间形成一个正方形.
由此可得:正六边形的一个内角,围成一圈后中间形成的正多边形的一个内角,,所以用6个全等的正六边形按这种方式拼接,围成一圈后中间形成一个正六边形.
河北25.如图14,点在轴的正半轴上,,,.点从点出发,沿轴向左以每秒1个单位长的速度运动,运动时间为秒.
(1) 求点的坐标;
(2) 当时,求的值;
(3) 以点为圆心,为半径的随点的运动而变化,当与四边形的边(或边所在的直线)相切时,求的值.
[解析](1)如图,,是直角三角形,故,即;
(2),在中,;
(3) 以点为圆心,为半径的随点的运动而变化,与四边形的边相切,有三种情况:
①与边相切时,是切点,如图,此时,,
, ,
②与边相切时,是切点,如图,此时,重合, ,
③与边相切时,是切点,如图,此时,,设,则在中,由勾股定理得:,
,
综上所述,满足条件的值共有三个,即,1,或4,或5.6.
26.如图和图,在中,,
探究 如图,于点,则_______,_______, 的面积=___________.
拓展 如图,点在上(可与点重合),分别过点作直线的垂线,垂足为.设,(当点与点重合时,我们认为=0.
(1)用含或的代数式表示及;
(2)求与的函数关系式,并求的最大值和最小值.
(3)对给定的一个值,有时只能确定唯一的点,指出这样的的取值范围.
发现 请你确定一条直线,使得三点到这条直线的距离之和最小,并写出这个最小值.
[解析] 探究 在中,
,于是
.
河南卷8、如图,已知为的直径,切于点A, 则下列结论不一定正确的是
A. B. C. D.
【解析】有AB为直径,AD为切线可知: A正确
∵ 同弧所对的圆周角等于圆心角的一半
∴ ∴ B正确
由“同弧所对的圆周角等于圆心角的一半”可以判断C正确
15、如图,在中,点D是BC边上一动点(不与点B、C重合),过点D作DE⊥BC交AB边于点E,将沿直线DE翻折,点B落在射线BC上的点F处,当△AEF为直角三角形时,BD的长为
【解析】由题意可知:
①当F在BC之间时,由翻折可知:BE=EF,,
由图可知:。设则
∴,解得
②当F在BC外部时,由翻折可知:BE=EF,,
由画图可知:,很容易得到:
可以得到:AE=DE。设∴。
∴.∴
22、(10分)类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整.
原题:如图1,在中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若,求的值。
(1)尝试探究 在图1中,过点E作交BG于点H,则AB和EH的数量关系是 ,CG和EH的数量关系是 , 的值是
【解析】∵, ∴
∵E为BC中点,,∴H为BG中点, ∴CG=2EH
四边形ABCD为菱形,AB=BC=CD=DA=3EH ∴
(2)类比延伸如图2,在原题的条件下,若则的值是 (用含的代数式表示),试写出解答过程。
作EH∥AB交BG于点H,则∴
∵AB=CD,∴ EH∥AB∥CD,∴
∴,∴CG=2EH ∴
(3)拓展迁移 如图3,梯形ABCD中,DC∥AB,点E是BC延长线上一点,
AE和BD相交于点F,若,则的值是 (用含的代数式表示).
【解析】过E作EH∥AB,交BD延长线于点H
由题意可知:EH∥DC∥AB ∴
又∵ 化简得:
23、如图,在平面直角坐标系中,直线与抛物线交于A,B两点,点A在轴上,点B的纵坐标为3.点P是直线AB下方的抛物线上一动点(不与A,B重合),过点P作轴的垂线交直线AB与点C,作PD⊥AB于点D
(1)求及的值
(2)设点P的横坐标为
①用含的代数式表示线段PD的长,并求出线段PD长的最大值;
②连接PB,线段PC把分成两个三角形,是否存在适合的值,使这两个三角形的面积之比为9:10?若存在,直接写出值;若不存在,说明理由.
【解析】(1)由,得到∴ 由,得到∴
∵经过两点,∴
B
C
D
X
O
P
A
Y
∴
当时。解得 当时,解得
黑龙江大庆
10.如图所示,将一个圆盘四等分,并把四个区域分别标上I、Ⅱ、Ⅲ、Ⅳ,只有区域I为感应区域,中心角为60°的扇形AOB绕点0转动,在其半径OA上装有带指示灯的感应装置,当扇形AOB与区域I有重叠(原点除外)的部分时,指示灯会发光,否则不发光,当扇形AOB任意转动时,指示灯发光的概率为【 】
A. B C. D.
【分析】如图,∵当扇形AOB落在区域I时,指示灯会发光;
当扇形AOB落在区域Ⅱ的∠FOC(∠FOC=60°)内部时,指示灯会发光;
当扇形AOB落在区域Ⅳ的∠DOE(∠DOE=60°)内部时,指示灯会发光,
∴指示灯发光的概率为:。故选D。
18.用八个同样大小的小立方体粘成一个大立方体如图1,得到的几何体的三视图如图2所示,若小明从八个小立方体中取走若干个,剩余小立方体保持原位置不动,并使得到的新几何体的三视图仍是图2,则他取走的小立方体最多可以是 ▲ 个.
【分析】由于从八个小立方体中取走若干个,剩余小立方体保持原位置不动,并使得到的新几何体的三视图都相同,由主视图可知有2层2列,由左视图可知有2层2行,由俯视图可知最少有4个小立方体,所以下层4个小立方体不变,同时上层每一横行和每一竖列上都有一个小立方体。因此,取走的小立方体最多可以是2个,即上层一条对角线上的2个。
黑龙江大庆27.在直角坐标系中,C(2,3),C′(-4,3), C″(2,1),D(-4,1),A(0,),B(,O)( 0).
(1)结合坐标系用坐标填空.
点C与C′关于点 对称; 点C与C″关于点 对称; 点C与D关于点 对称
(2)设点C关于点(4,2)的对称点是点P,若△PAB的面积等于5,求值.
【答案】解:(1)(﹣1,3);(2,2);(﹣1,2)。
(2)点C关于点(4,2)的对称点P(6,1),△PAB的面积=(1+a)×6﹣a2﹣×1×(6﹣a)=5,
整理得,a2﹣7a+10=0,解得a1=2,a2=5。所以,a的值为2或5。
28. 已知半径为1cm的圆,在下面三个图中AC=10cm,AB=6cm,BC=8cm,在图2中∠ABC=90°.
(1)如图1,若将圆心由点A沿AC方向运动到点C,求圆扫过的区域面积;
(2)如图2,若将圆心由点A沿ABC方向运动到点C,求圆扫过的区域面积;
(3)如图3,若将圆心由点A沿ABCA方向运动回到点A.
则I)阴影部分面积为_ ___;Ⅱ)圆扫过的区域面积为__ __.
【答案】解:(1)由题意得,圆扫过的面积=DE×AC+πr2=(20+π)cm2。
(2)圆扫过的区域面积=AB的面积+BC的面积-一个圆的面积。
结合(1)的求解方法,可得所求面积
=(2r×AB+πr2)+(2r×BC+πr2)﹣πr2=2r(AB+BC)+πr2=(28+π)cm2。
(3)I) cm2;Ⅱ)(+π)cm2。
黑龙江哈尔滨10.李大爷要围成一个矩形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长应恰好为24米.要围成的菜园是如图所示的矩形ABCD.设BC边的长为x米,AB边的长为y米,则y与x之间的函数关系式是【 】.
(A)y=-2x+24(0
OB.请解答下列问题:
(1)求直线AB的解析式;
(2)若P为AB上一点,且;,求过点P的反比例函数的解析式;
(3)在坐标平面内是否存在点Q,使得以A、P、O、Q为顶点的四边形是等腰梯形? 若存在,请直接写出点Q的坐标;若不存在,请说明理由.
【答案】解:(1)解x2-12x+32=0得x1=4,x2=8。
∵OA、OB的长分别是关于x的方程x2-12x+32=0的两根,且OA>OB,
∴OA=8,OB=4。∴A(-8,0),B(0,4)。
设直线AB的解析式为,则 ,解得。∴直线AB的解析式为。
(2)过点P作PH⊥x轴于点H。设P(x,y),由AH= x+8。
∵,∴,即。 解得 x=-6。
∵点P在上,∴。∴P(-6,1)。
设过点P的反比例函数的解析式为,则。∴。
∴点P的反比例函数的解析式为。
(3)存在。点Q的坐标为(-2,1)或或。
黑龙江绥化11.长为20,宽为a的矩形纸片(10<a<20),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去,若在第n次操作后,剩下的矩形为正方形,则操作停止.当n=3时,a的值为 ▲ .
20.如图,在平行四边形ABCD中,E是CD上的一点,DE:EC=2:3,连接AE、BE、BD,且AE、BD交于点F,则S△DEF:S△EBF:S△ABF=【 】
A.2:5:25 B.4:9:25 C.2: 3:5 D.4:10:25
【分析】由DE:EC=2:3得DE:DC=2:5,根据平行四边形对边相等的性质,得DE:AB=2:5
由平行四边形对边平行的性质易得△DFE∽△BFA ∴DF:FB= DE:AB=2:5,S△DEF:S△ABF=4:25。
又∵S△DEF和S△EBF是等高三角形,且DF:FB =2:5,∴S△DEF:S△EBF =2:5=4:10。
∴S△DEF:S△EBF:S△ABF =4:10:25。故选D。
黑龙江绥化27.在实施“中小学校舍安全工程”之际,某市计划对A、B两类学校的校舍进行改造,根据预算,改造一所A类学校和三所B类学校的校舍共需资金480万元,改造三所A类学校和一所B类学校的校舍共需资金400万元.
(1)改造一所A类学校的校舍和一所B类学校的校舍所需资金分别是多少万元?
(2)该市某县A、B两类学校共有8所需要改造.改造资金由国家财政和地方财政共同承担,若国家财政拨付的改造资金不超过770万元,地方财政投入的资金不少于210万元,其中地方财政投入到A、B两类学校的改造资金分别为每所20万元和30万元,请你通过计算求出有几种改造方案,每个方案中A、B两类学校各有几所?
【答案】解:(1)设改造一所A类学校的校舍需资金x万元,改造一所B类学校的校舍所需资金y万元,
则 ,解得 。
答:改造一所A类学校和一所B类学校的校舍分别需资金90万元,130万元。
(2)设A类学校应该有a所,则B类学校有(8-a)所.
则 ,解得 。∴1≤a≤3,即a=1,2,3。
∴共有3种改造方案:方案一:A类学校有1所,B类学校有7所;方案二:A类学校有2所,B类学校有6所;方案三:A类学校有3所,B类学校有5所。
28.如图,四边形ABCD为矩形,C点在x轴上,A点在y轴上,D点坐标是(0,0),B点坐标是(3,4),矩形ABCD沿直线EF折叠,点A落在BC边上的G处,E、F分别在AD、AB上,且F点的坐标是(2,4).
(1)求G点坐标; (2)求直线EF解析式;
(3)点N在x轴上,直线EF上是否存在点M,使以M、N、F、G为顶点的四边形是平行四边形?若存在,请直接写出M点的坐标;若不存在,请说明理由.
【答案】解:(1)由已知得,FG=AF=2,FB=1。
∵四边形ABCD为矩形,∴∠B=90°。∴。∴G点的坐标为(3,4-)。
(2)设直线EF的解析式是y=kx+b,在Rt△BFG中,,∴∠BFG=60°。∴∠AFE=∠EFG=60°。
∴AE=AFtan∠AFE=2tan60°=2。∴E点的坐标为(0,4-2)。又F点的坐标是(2,4),
∴, 解得。∴直线EF的解析式为。
(3)存在。M点的坐标为(),(),( )。
分FG为平行四边形边和对角线两种情况讨论,探究可能的平行四边形的形状:
若以M、N、F、G为顶点的四边形是平行四边形,则可能存在以下情形:
①FG为平行四边形的一边,且N点在x轴正半轴上,如图1所示。
过M1点作M1H⊥x轴于点H,易证△M1HN1≌△GBF,∴M1H=GB=,即yM1=。
由直线EF解析式,求出。∴M1()。
②FG为平行四边形的一边,且N点在x轴负半轴上,如图2所示。仿照与①相同的办法,可求得M2()。
③FG为平行四边形的对角线,如图3所示。过M3作FB延长线的垂线,垂足为H.易证△M3FH≌△GN3C,
则有M3H=CG=4,所以M3的纵坐标为8-。代入直线EF解析式,得到M3的横坐标为。
∴M3()。
综上所述,存在点M,使以M、N、F、G为顶点的四边形是平行四边形,点M的坐标为:M1(),M2(),M3( )。
湖北鄂州10.在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,………按这样的规律进行下去,第2012个正方形的面积为( )
A. B. C. D. 【答案】D。
x
y
O
B
C
Wwwzkucom
(2) 已知,如图,△OBC中是直角三角形,OB与x轴正半轴重合,∠OBC=90°,且OB=1,BC=,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的m倍,使OB1=OC,得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的m倍,使OB2=OC1,得到△OB2C2,……,如此继续下去,得到△OB2012C2012,则m= 。点C2012的坐标是 。
【答案】2;(22011,-22011)。
湖北鄂州23、某私营服装厂根据2011年市场分析,决定2012年调整服装制作方案,准备每周(按120工时计算)制作西服、休闲服、衬衣共360件,且衬衣至少60件。已知每件服装的收入和所需工时如下表:
服装名称
西服
休闲服
衬衣
工时/件
收入(百元)/件
3
2
1
设每周制作西服x件,休闲服y件,衬衣z件。
(1) 请你分别从件数和工时数两个方面用含有x,y 的代数式表示衬衣的件数z。
(2) 求y与x之间的函数关系式。
(3) 问每周制作西服、休闲服、衬衣各多少件时,才能使总收入最高?最高总收入是多少?
【答案】解:(1)从件数方面:z=360-x-y, 从工时数方面:由x+y+z=120整理得:z=480-2x-y。
(2)由(1)得360-x-y=480-2x-y,整理得:y=360-3x。
(3)由题意得总收入s=3x+2y+z=3x+2(360-3x)+2x=-x+720
由题意得,解得30≤x≤120。由一次函数的性质可知,当x=30的时候,s最大,
即当每周生产西服30件,休闲服270件,衬衣60件时,总收入最高,最高总收入是690百元。
24、已知:如图一,抛物线与x轴正半轴交于A、B两点,与y轴交于点C,直线经过A、C两点,且AB=2.
(1)求抛物线的解析式;
(2)若直线DE平行于x轴并从C点开始以每秒1个单位的速度沿y轴正方向平移,且分别交y轴、线段BC于点E,D,同时动点P从点B出发,沿BO方向以每秒2个单位速度运动,(如图2);当点P运动到原点O时,直线DE与点P都停止运动,连DP,若点P运动时间为t秒 ;设,当t 为何值时,s有最小值,并求出最小值。
(3)在(2)的条件下,是否存在t的值,使以P、B、D为顶点的三角形与△ABC相似;若存在,求t的值;若不存在,请说明理由。
【答案】解:(1)如图,由抛物线y=ax2+bx-2得:C(0,-2),∴OA=OC=2,∴A(2,0),
∵△ABC的面积为2,∴AB=2,∴B(4,0),∴设抛物线的解析式为y=a(x-2)(x-4),代入点C(0,-2),
a=-1 4 ,∴抛物线的解析式为y= -1 4 (x-2)(x-4)=-14 x2+32 x-2,
答:抛物线的解析式为y=-1 4 x2+3 2 x-2.
(2)解:由题意:CE=t,PB=2t,OP=4-2t,∵ED∥BA 可得:ED OB =CE CO ,即ED 4 =CE 2 ,∴ED=2CE=2t,
①1 ED +1 OP =1 2t +1 4-2t =4 2t(4-2t) =1 -t2+2t ,
∵当t=1时,-t2+2t有最大值1,∴当t=1时1 ED +1 OP 的值最小,最小值为1.
答:当t为1时,1 ED +1 OP 的值最小,最小值是1.
②解:由题意可求:CD= 5 t,CB=2 5 ,∴BD=2 5 - 5 t,
∵∠PBD=∠ABC,∴以P、B、D为顶点的三角形与△ABC相似有两种情况:
当BP AB =BD BC 时,即2t 2 =2 5 - 5 t 2 5 ,解得:t=2 3 ,
当BP BD =BC BA 时,即2t 2 5 - 5 t =2 5 2 ,解得:t=10 7 ,
当t=2 3 或t=10 7 时,以P、B、D为顶点的三角形与△ABC相似.
答:存在t的值,使以P,B,D为顶点的三角形与△ABC相似,t的值是2 3 或10 7 .
湖北恩施12.如图,菱形ABCD和菱形ECGF的边长分别为2和3,∠A=120°,则图中阴影部分的面积是【 】
A. B.2 C.3 D.
【分析】如图,设BF、CE相交于点M,∵菱形ABCD和菱形ECGF的边长分别为2和3,
∴△BCM∽△BGF,∴,即。解得CM=1.2。∴DM=2﹣1.2=0.8。
∵∠A=120°,∴∠ABC=180°﹣120°=60°。∴菱形ABCD边CD上的高为2sin60°=2×,
菱形ECGF边CE上的高为3sin60°=3×。∴阴影部分面积=S△BDM+S△DFM=×0.8×+×0.8×。故选A。
16.观察数表 根据表中数的排列规律,则B+D= ▲ .
【分析】∵仔细观察每一条虚线或与虚线平行的直线上的数字从左至右相加等于最上而的一个数字,
∴1+4+3=B,1+7+D+10+1=34。∴B=8,D=15。∴B+D=8+15=23。
23.如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.
(1)求证:BC是⊙O的切线; (2)连接AF,BF,求∠ABF的度数;
(3)如果CD=15,BE=10,sinA=,求⊙O的半径.
【答案】解:(1)证明:连接OB,∵OB=OA,CE=CB,∴∠A=∠OBA,∠CEB=∠ABC。
又∵CD⊥OA,∴∠A+∠AED=∠A+∠CEB=90°。∴∠OBA+∠ABC=90°。∴OB⊥BC。
∴BC是⊙O的切线。
(2)连接OF,AF,BF,∵DA=DO,CD⊥OA,∴△OAF是等边三角形。
∴∠AOF=60°。∴∠ABF=∠AOF=30°。
(3)过点C作CG⊥BE于点G,由CE=CB,∴EG=BE=5。易证Rt△ADE∽Rt△CGE,
∴sin∠ECG=sin∠A=,∴。∴。
又∵CD=15,CE=13,∴DE=2,由Rt△ADE∽Rt△CGE得,即,解得。
∴⊙O的半径为2AD=。
24.如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N.其顶点为D.
(1)抛物线及直线AC的函数关系式;
(2)设点M(3,m),求使MN+MD的值最小时m的值;
(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;
(4)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.
【答案】解:(1)由抛物线y=﹣x2+bx+c过点A(﹣1,0)及C(2,3)得,
,解得。∴抛物线的函数关系式为。
设直线AC的函数关系式为y=kx+n,由直线AC过点A(﹣1,0)及C(2,3)得
,解得。∴直线AC的函数关系式为y=x+1。
(2)作N点关于直线x=3的对称点N′,
令x=0,得y=3,即N(0,3)。∴N′(6, 3)
由得D(1,4)。
设直线DN′的函数关系式为y=sx+t,则
,解得。
∴故直线DN′的函数关系式为。
根据轴对称的性质和三角形三边关系,知当M(3,m)在直线DN′上时,MN+MD的值最小,
∴。
∴使MN+MD的值最小时m的值为。
(3)由(1)、(2)得D(1,4),B(1,2),
①当BD为平行四边形对角线时,由B、C、D、N的坐标知,四边形BCDN是平行四边形,此时,点E与点C重合,即E(2,3)。
②当BD为平行四边形边时,
∵点E在直线AC上,∴设E(x,x+1),则F(x,)。
又∵BD=2
∴若四边形BDEF或BDFE是平行四边形时,BD=EF。
∴,即。
若,解得,x=0或x=1(舍去),∴E(0,1)。
若,解得,,∴E或E。
综上,满足条件的点E为(2,3)、(0,1)、、。
(4)如图,过点P作PQ⊥x轴交AC于点Q;过点C作CG⊥x轴于点G,
设Q(x,x+1),则P(x,﹣x2+2x+3)。
∴。
∴
。
∵,
∴当时,△APC的面积取得最大值,最大值为。
湖北黄冈8.如图,在Rt△ABC中,∠C=90°,AC=BC=6cm,点P 从点A 出发,沿AB方向以每秒cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm 的速度向终点C 运动,将△PQC沿BC翻折,点P的对应点为点P′.设Q点运动的时间t秒,若四边形QPCP′为菱形,则t的值为【 】
A. B. 2 C. D. 4
【分析】如图,过点P作PD⊥AC于点D,连接PP′。
由题意知,点P、P′关于BC对称,∴BC垂直平分PP′。
∴QP=QP′,PE=P′E。
∴根据菱形的性质,若四边形QPCP′是菱形则CE=QE。
∵∠C=90°,AC=BC,∴∠A=450。
∵AP=t,∴PD= t。
易得,四边形PDCE是矩形,∴CE=PD= t,即CE=QE= t。
又BQ= t,BC=6,∴3 t=6,即t=2。
∴若四边形QPCP′为菱形,则t的值为2。故选B。
16.某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下4个结论:
①快递车从甲地到乙地的速度为100千米/时;②甲、乙两地之间的距离为120千米;
③图中点B的坐标为(,75); ④快递车从乙地返回时的速度为90千米/时.以上4个结论中正确的是 (填序号)
【分析】①设快递车从甲地到乙地的速度为v1千米/时,
由已知,货车的速度为60千米/时,
由图象知,货车行驶时间3小时时,两车相距120千米,得
,解得v1=100。
∴快递车从甲地到乙地的速度为100千米/时。故结论①正确。
② 由图象知,快递车行驶3小时到达乙地,∴甲、乙两地之间的距离为3×100=300(千米)。
故结论②错误。
③ ∵快递车到达乙地后卸完物品再另装货物共用45分钟,即小时,
∴点B的横坐标为3+。
又∵小时货车行驶了(千米),
∴此时两车相距120-45=75(千米),即点B的纵坐标为75。
∴图中点B的坐标为(,75)。故结论③正确。
④ 设快递车从乙地返回时的速度为v2千米/时,
由③和图象可得,,解得v2=90。
∴快递车从乙地返回时的速度为90千米/时。故结论④正确。
综上所述,结论①③④正确。
湖北黄冈24.某科技开发公司研制出一种新型产品,每件产品的成本为2400 元,销售单价定为3000 元.在该产品的试销期间,为了促销,鼓励商家购买该新型产品,公司决定商家一次购买这种新型产品不超过10 件时,每件按3000 元销售;若一次购买该种产品超过10 件时,每多购买一件,所购买的全部产品的销售单价均降低10 元,但销售单价均不低于2600 元.
(1)商家一次购买这种产品多少件时,销售单价恰好为2600 元?
(2)设商家一次购买这种产品x 件,开发公司所获的利润为y 元,求y(元)与x(件)之间的函数关系式,并写出自变量x 的取值范围.
(3)该公司的销售人员发现:当商家一次购买产品的件数超过某一数量时,会出现随着一次购买的数量的增多,公司所获的利润反而减少这一情况.为使商家一次购买的数量越多,公司所获的利润越大,公司应将最低销售单价调整为多少元?(其它销售条件不变)
【答案】解:(1)设件数为x,依题意,得3000-10(x-10)=2600,解得x=50。
答:商家一次购买这种产品50件时,销售单价恰好为2600元。
(2)当0≤x≤10时,y=(3000-2400)x=600x;
当10<x≤50时,y=[3000-10(x-10)-2400]x,即y=-10x2+700x;
当x>50时,y=(2600-2400)x=200x。
∴。
(3)由y=-10x2+700x可知抛物线开口向下,当时,利润y有最大值,
此时,销售单价为3000-10(x-10)=2750元,
答:公司应将最低销售单价调整为2750元。
25.如图,已知抛物线的方程C1:与x 轴相交于点B、C,与y 轴相交于点E,且点B 在点C 的左侧.
(1)若抛物线C1过点M(2,2),求实数m 的值.(2)在(1)的条件下,求△BCE的面积.
(3)在(1)的条件下,在抛物线的对称轴上找一点H,使BH+EH最小,并求出点H的坐标.
(4)在第四象限内,抛物线C1上是否存在点F,使得以点B、C、F为顶点的三角形与△BCE相似?若存在,求m的值;若不存在,请说明理由.
【答案】解:(1)∵抛物线C1过点M(2,2),∴,解得m=4。
(2)由(1)得。
令x=0,得。∴E(0,2),OE=2。
令y=0,得,解得x1=-2,x=4。
∴B(-2,,0),C(4,0),BC=6。
∴△BCE的面积=。
(3)由(2)可得的对称轴为x=1。
连接CE,交对称轴于点H,由轴对称的性质和两点之间线段最短的性质,知此时BH+EH最小。
设直线CE的解析式为,则
,解得。∴直线CE的解析式为。
当x=1时,。∴H(1,)。
(4)存在。分两种情形讨论:
①当△BEC∽△BCF时,如图所示。
则,∴BC2=BE•BF。
由(2)知B(-2,0),E(0,2),即OB=OE,
∴∠EBC=45°,∴∠CBF=45°。
作FT⊥x轴于点F,则BT=TF。
∴令F(x,-x-2)(x>0),
又点F在抛物线上,∴-x-2=,
∵x+2>0(∵x>0),∴x=2m,F(2m,-2m-2)。
此时,
又BC2=BE•BF,∴(m+2)2= •,解得m=2±。
湖北黄石10.如图所示,已知A,B为反比例函数图像上的两点,动点P在x正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是【 】
A. B. C. D.
【分析】∵把A,B分别代入反比例函数 得:y1=2,y2= ,∴A( ,2),B(2, )。
∵在△ABP中,由三角形的三边关系定理得:|AP-BP|<AB,
∴延长AB交x轴于P′,当P在P′点时,PA-PB=AB,
即此时线段AP与线段BP之差达到最大。
设直线AB的解析式是y=kx+b,把A、B的坐标代入得:
,解得:。∴直线AB的解析式是。
当y=0时,x= ,即P( ,0)。故选D。
16.如图所示,已知A点从点(1,0)出发,以每秒1个单位长的速度沿着x轴的正方向运动,经过t秒后,以O、A为顶点作菱形OABC,使B、C点都在第一象限内,且∠AOC=600,又以P(0,4)为圆心,PC为半径的圆恰好与OA所在直线相切,则t= ▲ .
【分析】∵已知A点从(1,0)点出发,以每秒1个单位长的速度沿着x轴的正方向运动,
∴经过t秒后,∴OA=1+t。,
∵四边形OABC是菱形,∴OC=1+t。,
当⊙P与OA,即与x轴相切时,如图所示,则切点为O,此时PC=OP。
过点P作PE⊥OC,垂足为点E。
∴OE=CE=OC,即OE=(1+t)。
在Rt△OPE中,OP=4,∠OPE=900-∠AOC=30°,
∴OE=OP•cos30°=,即。
∴。
∴当PC为半径的圆恰好与OA所在直线相切时,。
湖北黄石24.如图1所示:等边△ABC中,线段AD为其内角平分线,过D点的直线B1C1⊥AC于C1交AB的延长线于B1.
(1)请你探究:,是否成立?
(2)请你继续探究:若△ABC为任意三角形,线段AD为其内角平分线,请问一定成立吗?并证明你的判断.
(3)如图2所示Rt△ABC中,∠ACB=900,AC=8,,E为AB上一点且AE=5,CE交其内角角平分线AD与F.试求的值.
【答案】解:(1)∵线段AD为等边△ABC内角平分线,∴根据三线合一,得CD=DB。
∴。
过点D作DN⊥AB于点H。
∵线段AD为等边△ABC内角平分线,∴C1D=ND。
∵等边△ABC中,B1C1⊥AC,∴∠B1=300。
∴。
∴,都成立。
(2)结论仍然成立。证明如下:
如图,ΔABC为任意三角形,过B点作BE∥AC交 AD的延长线于点G 。
∵∠G=∠CAD=∠BAD,∴BG=AB。
又ΔGBD∽ΔACD ,
∴,即。
∴对任意三角形结论仍然成立。
﹙3﹚如图,连接ED。
∵AD为ΔABC的内角角平分线,AC=8,,
∴由(2)得, 。
又∵AE=5,∴EB=AB-AE=。∴。
∴。∴DE∥AC。 ∴ΔDEF∽ΔACF。
∴。
25.已知抛物线C1的函数解析式为,若抛物线C1经过点,方程的两根为,,且。
(1)求抛物线C1的顶点坐标.
(2)已知实数,请证明:≥,并说明为何值时才会有.
(3)若抛物线先向上平移4个单位,再向左平移1个单位后得到抛物线C2,设, 是C2上的两个不同点,且满足: ,,.请你用含有的表达式表示出△AOB的面积S,并求出S的最小值及S取最小值时一次函数OA的函数解析式。
(参考公式:在平面直角坐标系中,若,,则P,Q两点间的距离)
【答案】解:(1)∵抛物线过(0,-3)点,∴-3a=-3。∴a=1 。
∴y=x2+bx-3
∵x2+bx-3=0的两根为x1,x2且,
∴=4且b<0。∴b=-2。
∴。
∴抛物线C1的顶点坐标为(1,-4)。
别解:由题意可求抛物线C2的解析式为:y=x2。
∴A(m,m2),B(n,n2)。
过点A、B作x轴的垂线,垂足分别为C、D,
则
由 得 ,即。∴。
∴。
∴SΔAOB的最小值为1,此时m=1,A(1,1)。
∴直线OA的一次函数解析式为y=x。
湖北荆州10.已知:顺次连接矩形各边的中点,得到一个菱形,如图①;再顺次连接菱形各边的中点,得到一个新的矩形,如图②;然后顺次连接新的矩形各边的中点,得到一个新的菱形,如图③;如此反复操作下去,则第2012个图形中直角三角形的个数有【 】
A. 8048个 B. 4024个 C. 2012个 D. 1066个
【分析】写出前几个图形中的直角三角形的个数,并找出规律:
第1个图形,有4个直角三角形,第2个图形,有4个直角三角形,
第3个图形,有8个直角三角形,第4个图形,有8个直角三角形,
…,
依次类推,当n为奇数时,三角形的个数是2(n+1),当n为偶数时,三角形的个数是2n个,
所以,第2012个图形中直角三角形的个数是2×2012=4024。故选B。
18.如图(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P沿折线BE﹣ED﹣DC运动到点C时停止,点Q沿BC运动到点C时停止,它们运动的速度都是1cm/秒.设P、Q同发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(曲线OM为抛物线的一部分),则下列结论:①AD=BE=5;②cos∠ABE=;③当0<t≤5时,;④当秒时,△ABE∽△QBP;其中正确的结论是 ▲ (填序号).
湖北十堰10.如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO;⑤S△AOC+S△AOB=.其中正确的结论是( A )
A.①②③⑤ B.①②③④ C.①②③④⑤ D.①②③
【解答】解:由题意可知,∠1+∠2=∠3+∠2=60°,∴∠1=∠3,
又∵OB=O′B,AB=BC,
∴△BO′A≌△BOC,又∵∠OBO′=60°,
∴△BO′A可以由△BOC绕点B逆时针旋转60°得到,
故结论①正确;
如图①,连接OO′,∵OB=O′B,且∠OBO′=60°,
∴△OBO′是等边三角形,∴OO′=OB=4.故结论②正确;
∵△BO′A≌△BOC,∴O′A=5.
在△AOO′中,三边长为3,4,5,这是一组勾股数,
∴△AOO′是直角三角形,∠AOO′=90°,
∴∠AOB=∠AOO′+∠BOO′=90°+60°=150°,
故结论③正确;
S四边形AOBO′=S△AOO′+S△OBO′=,
故结论④错误;
如图②所示,将△AOB绕点A逆时针旋转60°,使得AB与AC重合,点O旋转至O″点.
易知△AOO″是边长为3的等边三角形,△COO″是边长为3、4、5的直角三角形,
则S△AOC+S△AOB=S四边形AOCO″=S△COO″+S△AOO″= ,故结论⑤正确.
综上所述,正确的结论为:①②③⑤.故选A.
16.如图,直线y=6x,y=2 3 x分别与双曲线y=k x 在第一象限内交于点A,B,若S△OAB=8,则k= 6 .
【解答】解:如图,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,
设点A(x1,),B(x2,),联立,解得,
联立,解得,
S△OAB=S△OAC+S梯形ACDB-S△OBDx2 ,
,∵S△OAB=8,∴,解得k=6.故答案为:6.
24.如图1,⊙O是△ABC的外接圆,AB是直径,OD∥AC,且∠CBD=∠BAC,OD交⊙O于点E.
(1)求证:BD是⊙O的切线;
(2)若点E为线段OD的中点,证明:以O、A、C、E为顶点的四边形是菱形;
(3)作CF⊥AB于点F,连接AD交CF于点G(如图2),求FG FC 的值.
【解答】(1)证明:∵AB是⊙O的直径,∴∠BCA=90°,∴∠ABC+∠BAC=90°,
又∵∠CBD=∠BA,∴∠ABC+∠CBD=90°,∴∠ABD=90°,∴OB⊥BD,∴BD为⊙O的切线;
(2)证明:连CE、OC,BE,如图,
∵OE=ED,∠OBD=90°,
∴BE=OE=ED,
∴△OBE为等边三角形,
∴∠BOE=60°,
又∵AC∥OD,
∴∠OAC=60°,
又∵OA=OC,
∴AC=OA=OE,
∴AC∥OE且AC=OE,
∴四边形OACE是平行四边形,
而OA=OE,∴四边形OACE是菱形;
(3)解:∵CF⊥AB,∴∠AFC=∠OBD=90°,而AC∥OD,∴∠CAF=∠DOB,∴Rt△AFC∽Rt△OBD,
∴,即,又∵FG∥BD,∴△AFG∽△ABD,∴,即,
∴,∴.
25.抛物线y=-x2+bx+c经过点A、B、C,已知A(-1,0),C(0,3).
(1)求抛物线的解析式;
(2)如图1,P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BDC的面积最大时,求点P的坐标;
(3)如图2,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,请指出实数m的变化范围,并说明理由.
【解答】解:(1)由题意得:,解得:,∴抛物线解析式为;
(2)令,∴x1= -1,x2=3,即B(3,0),设直线BC的解析式为y=kx+b′,
∴,解得:,∴直线BC的解析式为,
设P(a,3-a),则D(a,-a2+2a+3),
∴PD=(-a2+2a+3)-(3-a)=-a2+3a,
∴S△BDC=S△PDC+S△PDB
,
∴当时,△BDC的面积最大,此时P(,);
(3)由(1),y=-x2+2x+3=-(x-1)2+4,∴OF=1,EF=4,OC=3,过C作CH⊥EF于H点,则CH=EH=1,
当M在EF左侧时,∵∠MNC=90°,则△MNF∽△NCH,∴,
设FN=n,则NH=3-n,∴,即n2-3n-m+1=0,
关于n的方程有解,△=(-3)2-4(-m+1)≥0,得m≥,
当M在EF右侧时,Rt△CHE中,CH=EH=1,∠CEH=45°,即∠CEF=45°,
作EM⊥CE交x轴于点M,则∠FEM=45°,∵FM=EF=4,∴OM=5,即N为点E时,OM=5,∴m≤5,
综上,m的变化范围为:≤m≤5.
湖北随州10.如图,直线与反比例函数的图象在第一象限内交于A、B两点,交x轴的正半轴于C点,若AB:BC=(m一l):1(m>l)则△OAB的面积(用m表示)为( )
A. B. C. D. B
16.设a2+2a-1=0,b4-2b2-1=0,且1-ab2≠0,则= . 16.-32
湖北随州24.一列快车由甲地开往乙地,一列慢车由乙地开往甲地, 两车同时出发,匀速运动.快车离乙地的路程y1(km)与行驶的时间x(h)之间的函数关系,如图中线段AB所示;慢车离乙地的路程y2(km)与行驶的时间x(h)之间的函数关系,如图中线段0C所示。根据图象进行以下研究。
解读信息:
(1)甲、乙两地之间的距离为 km;(2)线段AB的解析式为 ; 线段OC的解析式为 ;
问题解决:
(3)设快、慢车之间的距离为y(km),求y与慢车行驶时间x(h)的函数关系式,并画出函数的图象。
24. (1)甲、乙两地之间的距离为 450 km; …………2分
(2)问题解决:线段AB的解析式为 y1=450-150 x (0≤x≤3); …………3分
线段OC的解析式为 y2=75x (0≤x≤6) ; …………3分
(3)y= …………2分
其图象为折线图AE-EF-FC
25.在-次数学活动课上,老师出了-道题:
(1)解方程x2-2x-3=0. 巡视后老师发现同学们解此题的方法有公式法、配方法和十字相乘法(分解因式法)。
接着,老师请大家用自己熟悉的方法解第二道题:
(2)解关于x的方程mx2+(m一3)x一3=0(m为常数,且m≠0). 老师继续巡视,及时观察、点拨大家.再接着,老师将第二道题变式为第三道题:
(3)已知关于x的函数y=mx2+(m-3)x-3(m为常数).
①求证:不论m为何值,此函数的图象恒过x轴、y轴上的两个定点(设x轴上的定点为A,y轴上的定点为C);
②若m≠0时,设此函数的图象与x轴的另一个交点为反B,当△ABC为锐角三角形时,求m的取值范围;当△ABC为钝角三角形时,观察图象,直接写出m的取值范围.
请你也用自己熟悉的方法解上述三道题.
25.解:(1)由x2-2x-3=0,得(x+1)(x-3)=0∴x1=1,x2=3
(2)方法一:由mx2+(m-3)x-3=0得(x+1)·(mx-3)=0 ∵m≠0, ∴x1=-1,x2=
方法2:由公式法: ∴x1=-1,x2=
(3)①1°当m=0时,函数y= mx2+(m-3)x-3为y=-3x-3,令y=0,得x=-1
令x=0,则y=-3. ∴直线y=-3x-3过定点A(-1,0),C(0,-3)
2°当m≠0时,函数y= mx2+(m-3)x-3为y=(x+1)·(mx-3)
∴抛物线y=(x+1)·(mx-3)恒过两定点A(-1,0),C(0,-3)和B(,0)
②当m>0时,由①可知抛物线开口向上,且过点A(-1,0),C(0,-3)和B(,0),
观察图象,可知,当⊿ABC为Rt⊿时,则⊿AOC∽⊿COB∴
∴∴32=1× ∴OB=9.即B(9,0)
∴当.即:m> 当m>时,⊿ABC为锐角三角形
②观察图象可知 当090º,
当m<0且m≠-3时,点B在x轴的负半轴上,B与A不重合.
∴⊿ABC中的∠ABC>90º ∴⊿ABC是钝角三角形. ∴当0
查看更多