中考数学函数复习专题
x
y
Ox
y
Ox
y
OO
y
x
第一讲:一次函数与反比例函数
1.一次函数与正比例函数的定义:
一次函数:一般地,y=kx+b 若(其中 k,b 为常数且 k≠0),那么 y 是 x 的一次函数
正比例函数:当 b=0, k≠0 时,y=kx,此时称 y 是 x 的正比例函数
2. 一次函数与正比例函数的区别与联系:
从解析式看:y=kx+b(k≠0,b≠0)是一次函数而 y=kx(k≠0,b≠0)是正比例函数,显然正比例函数是一次函数
的特例,一次函数是正比例函数的推广
从图象看:y=kx(k≠0)是过点(0,0)的一条直线,而 y=kx+b(k≠0)是过点(0,b)且与 y=kx 平行的一条直
线。
例 1:如图,已知直线 y=-x+2 与 x 轴,y 轴分别交于点 A 和点 B,另一直线 y=kx+b(k≠0)经过点 C(1,0),且
把△AOB 分成两部分。
(1)若△AOB 被分成的两部分面积相等,求 k 和 b 的值
3、反比例函数的图象 y = 是由两支曲线组成的。
(1) 当 k>0 时,两支曲线分别位于第一、三象限,
(2) 当 k<0 时,两支曲线分别位于第二、四象限.
例 2.(1)已知函数 的图象分布在第二、四象限内,则 的取值范围是_________
(2)若 ab<0,则函数 与 在同一坐标系内的图象大致可能是下图中的 ( )
(A) (B) (C) (D)
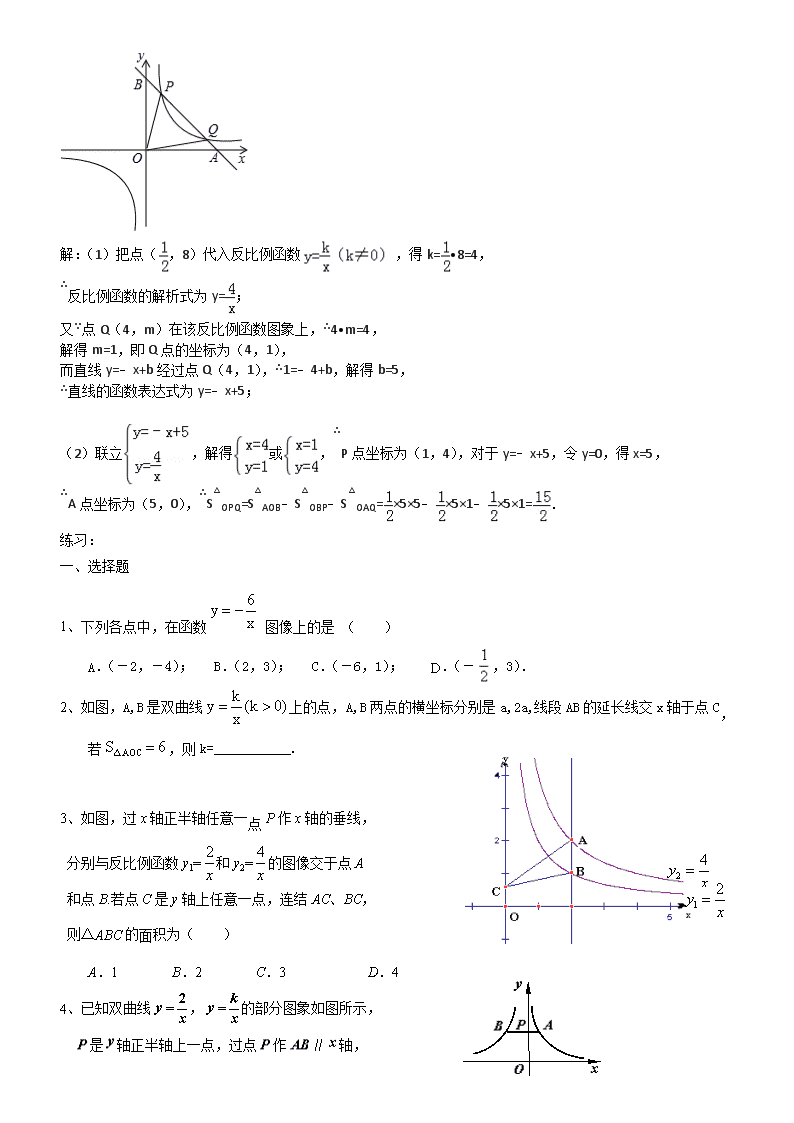
(2011•成都)如图,已知反比例函数 的图象经过点( ,8),直线 y=﹣x+b 经过该反比例函数
图象上的点 Q(4,m).
(1)求上述反比例函数和直线的函数表达式;
(2)设该直线与 x 轴、y 轴分别相交于 A、B 两点,与反比例函数图象的另一个交点为 P,连接 0P、OQ,求△OPQ
的面积.
k
x
1ky x
+= k
axy =
x
by =
O
B
A
C
2
4y x
=
1
2y x
=
解:(1)把点( ,8)代入反比例函数 ,得 k= •8=4,
∴反比例函数的解析式为 y= ;
又∵点 Q(4,m)在该反比例函数图象上,∴4•m=4,
解得 m=1,即 Q 点的坐标为(4,1),
而直线 y=﹣x+b 经过点 Q(4,1),∴1=﹣4+b,解得 b=5,
∴直线的函数表达式为 y=﹣x+5;
(2)联立 ,解得 或 ,∴P 点坐标为(1,4),对于 y=﹣x+5,令 y=0,得 x=5,
∴A 点坐标为(5,0),∴S△OPQ=S△AOB﹣S△OBP﹣S△OAQ= ×5×5﹣ ×5×1﹣ ×5×1= .
练习:
一、选择题
1、下列各点中,在函数 图像上的是 ( )
A .(-2,-4); B.(2,3); C.(-6,1); D.(- ,3).
2、如图,A,B 是双曲线 上的点,A,B 两点的横坐标分别是 a,2a,线段 AB 的延长线交 x 轴于点 C,
若 ,则 k=___________.
3、如图,过 x 轴正半轴任意一点 P 作 x 轴的垂线,
分别与反比例函数 y1= 和 y2= 的图像交于点 A
和点 B.若点 C 是 y 轴上任意一点,连结 AC、BC,
则△ABC 的面积为( )
A.1 B.2 C.3 D.4
4、已知双曲线 , 的部分图象如图所示,
是 轴正半轴上一点,过点 作 ∥ 轴,
x
6y −=
)0k(x
ky >=
6S AOC =△
2
x
4
x
2y x
= ky x
=
2
1
P y P AB x
P AB
x
y
O
O x
y
┐
分别交两个图象于点 .若 ,则 .
5、如图,点 A 在双曲线 上,且 OA=4,过 A 作 AC⊥ 轴,
垂足为 C, OA 的垂直平分线交 OC 于 B,则△ABC 周长为( )
A. B.5 C. D.
6、平面直角坐标系中,已知点 O(0,0)、A(0,2)、B(1,0),点 P 是反比例函数 图 象上的一个动点,
过点 P 作 PQ⊥x 轴,垂足为点 Q.若以点 O、P、Q 为顶点的三角形与△OAB 相似, 则相应的点 P 共有
( )
A.1 个 B.2 个 C.3 个 D.4 个
7、已知反比例函数的图象过点 M(-1,2),则此反比例函数的表达式为( )
A.y= B.y=- C.y= D.y=-
8、经过点 的双曲线的表达式是( ).
A. ; B. ; C. ; D.
9、如图,已知双曲线 经过直角三角形 OAB 斜边 OA
的中点 D,且与直角边 AB 相交于点 C.若点 A 的坐标为( ,4),
则△AOC 的面积为( )
A.12 B.9 C.6 D.4
10、如图,矩形 ABOC 的面积为 3,反比例函数 的图象过点 A,
则 k=( )
A. B. C. D.
11、已知反比例函数 的图象如图,则一元二次方程
根的情况是( )
A.有两个不等实根 B.有两个相等实根
C.没有实根 D.无法确定。
12、下列函数中,y 随 x 增大而减小的是( )
A.y=— B.y= C.y=- D. y= -x-1
13、如图,已知梯形 ABCO 的底边 AO 在 轴上,BC∥AO,AB⊥AO,
过点 C 的双曲线 交 OB 于 D,且 OD :DB=1 :2,
若△OBC 的面积等于 3,
1y x
= −
( 0)ky kx
= <
6−
2x x2
1
x
4
,A B 2PB PA= =k
6y x
= x
4 7 2 7 22
x
2
x
2
x2
1
x2
1
( )2,4
y 2x= 1
2
=y x
8y x
= 2y x=
x
ky =
3 5.1− 3− 6−
2ky x
−=
2 2(2 1) 1 0x k x k− − + − =
x
ky x
=
O A
BC
D
x
y
则 k 的值( )
A.等于 2 B.等于 C.等于 D.无法确定
14、反比例函数 与一次函数 y=mx-m(m≠0)在同一平面直角坐标系中的图像可能是( )
15、若反比例函数 y= 的图象经过点(-2,1),则此函数的图象一定经过点( )
A.(-2,-1) B. (2,-1) C. ( ,2) D. ( ,2)
16、如图所示,两个反比例函数 和 在第一象限内的图象依次
是 和 ,设点 在 上, ⊥ 轴于点 ,交 于点 ,
⊥ 轴于点 ,交 于点 ,则四边形 的面积为( )
A. B. C. D.
17、若点 都在反比例函数 的图象上,则( )
A. B. C. D.
18、下列函数中,y 随 x 的增大而减小的是( )
A. ; B. ; C. ; D. .
19、若反比例函数 的图象经过点(-1,2),则这个函数的图象一定经过点( )
A、(2,-1) B、( ,2) C、(-2,-1) D、( ,2)
20、若反比例函数 的图象位于第二、四象限内,则 m 的取值范围是( )
A.m>0 B.m<0 C.m>1 D.m<1
21、已知反比例函数的图象经过点(-1,2),则这个函数的图象位于( )
A.第一、三象限 B.第二、三象限 C.第二、四象限 D.第三、四象限
22、反比例函数 y= ,当 x>0 时,y 随 x 的增大而增大,那么 m 的取值范围是( )
(A)m<3 (B) m>3 (C)m<-3 (D) m>-3
二、填空题
1
3y x= 1
3y x= − 3y x
= 3y x
= −
3
4
24
5
x
my =
k
x
1
2
− 1
2
x
ky 1=
x
ky 2=
1C 2C P 1C PC x C 2C A
PD y D 2C B PAOB
21 kk + 21 kk − 21 kk ⋅ 221 kkk −⋅
1 2 3( 1, ) 2 3y− 、( ,y )、( ,y ) 5y x
=
1 2 3y y y< < 2 1 3y y y< < 1 2 3y y y> > 1 3 2y y y< <
ky x
=
1
2
− 1
2
x
my 1−=
x
m 3+
A
O
y
x
B
O
y
x
D
O
y
x
C
O
y
x
1 x
y
S1
S2 S3
P1
P2
P3
O 2 3 4
AB
P x
y
O
1、点 ,点 是双曲线 上的两点,若 ,则 ( 填 “ = ”、“ > ”、
“<”).
2、如果点 A、B 在一个反比例函数的图像上,点 A 的坐标为(1,2),点 B 横坐标为 2,那么 A、B 两点之间的
距离为 .
3、已知反比例函数的图像经过点(m,3)和(-3,2),则 m 的值为 .
4、若反比例函数的图象经过点(-2,-1),则这个函数的图象位于第___________象限.
5、设函数 与 的图象的交点坐标为( , ),则 的值为__ ___.
6、如果 , ,那么 .
7、某中学要在校园内划出一块面积是 100m2 的矩形土地做花圃,设这个矩形的相邻两边的长分别为 xm 和 ym,
那么 y 关于 x 的函数解析式是_________________.
8、反比例函数 y=
k
x 的图象与正比例函数 y=3x 的图象交于 O点 P(m,6),则反比例函数的关系式
是 .
9、如图,已知点 A 在双曲线 上,过点 A 作 AC⊥x 轴于点 C,OC= ,
线段 OA 的垂直平分线交 OC 于点 B,则△ABC 的周长为 .
10、若反比例函数 y=(k-1) 的图象经过第二、四象限,则 k= .
11、一个函数具有下列性质:
①它的图像经过点(-1,1);②它的图像在二、四象限内; ③在每个象限内,函数值 y 随自变量 x 的增
大而增大.则这个函数的解析式可以为 .
12、如图,在反比例函数 ( )的图象上,
有点 ,···, ,它们的横坐标依次为
1,2,3,4,···, .分别过这些点作 轴与 轴
的垂线,图中所构成的阴影部分的面积分别为
,···, ,则 的值为 .
13、如图,A 是反比例函数 y= 图象上一点,过点
A 作 AB⊥y 轴于点 B,点 P 在 x 轴上,△ABP 的面
积为 2,则 K 的值为_____________.
14、如图,△AOB 为等边三角形,点 B 的坐标为(-2,0),
过点 C(2,0)作直线 l 交 AO 于 D,交 AB 于 E,点 E
1 1( , )A x y 2 2( , )B x y 1 2 0x x< <
( ) kf x x
= ( )2 3f = − k =
2y x
= − 1y 2y
2y x
= 1y x= − a b 1 1
a b
−
xy 6= 3
2k -5x
xy 6= 0x >
1 2 3 4P P P P, , , nP
n x y
1 2 3S S S, , nS 10321 SSSS ++++
x
k
在某反比例函数图象上,当△ADE 和△DCO 的
面积相等时,那么该反比例函数解析式为 .
三、解答题
1、已知双曲线 和直线 AB 的图象交于点 A(-3,4),AC⊥x 轴于点 C.
(1)求双曲线 的解析式;
(2)当直线 AB 绕着点 A 转动时,与 x 轴的交点为 B(a,0),并与双曲线 另一支还有一个交点的情形下,求
△ABC 的面积 S 与 a 之间的函数关系式.,并指出 a 的取值范围.
2、已知反比例函数 的图像经过第二象限内的点A(-1,m),AB⊥x轴于点B,△AOB的面积为2.若直
线 经过点A,并且经过反比例函数 的图象上另一点C(n,一2).
⑴求直线 的解析式;
⑵设直线 与 x 轴交于点 M,求 AM 的长.
3、如图,在以 O 为原点的直角坐标系中,点 A、C 分别在 x 轴、y 轴的正半轴上,点 B(a,b)在第一象限,四
边形 OABC 是矩形,若反比例函数 (k>0,x>0)的图象与 AB 相交于点 D,与 BC 相交于点 E,且 BE=CE.
(1)求证:BD=AD;
(2)若四边形 ODBE 的面积是 9,求 k 的值.
ky x
=
ky x
=
ky x
=
x
ky =
baxy +=
x
ky =
baxy +=
baxy +=
x
ky =
4、如图,将—矩形 OABC 放在直角坐际系中,O 为坐标原点.点 A 在 x 轴正半轴上.点 E 是边 AB 上的—个动
点(不与点 A、B 重合),过点 E 的反比例函数 的图象与边 BC 交于点 F.
(1)若△OAE、△OCF 的而积分别为 .且 ,求 k 的值.
(2)若 OA=2,0C=4,问当点 E 运动到什么位置时,四边形 OAEF 的面积最大,其最大值为多少?
5、如图,在平面直角坐标系中,一次函数 y=-2x 的图像与反比例函数 的图像的一个交点为 A(-1,n).
(1) 求反比例函数 的解析式;
(2) 若 P 是坐标轴上的一点,且满足 PA=0A,直接写出 P 的坐标.
6、如图,一次函数 与反比例函数 在第一象限的图象交于点 ,且点 的横坐标为 1,过点
作 轴的垂线, 为垂足,若 ,求一次函数和反比例函数的解析式.
( 0)ky xx
= >
1 2S S、 1 2 =2S S+
ky x
=
ky x
=
y x b= + ky x
= B B B
y C 3
2BCOS∆ =
y
x
A
O
B
A
B(1,n)
1
-1
-2
n
y
O x
7、已如图,反比例函数 y=k
x 的图象与一次函数 y=mx+b 的图象交于两点 A(1,3) ,B(n,-1).
(1)求反比例函数与一次函数的函数关系式;
(2)根据图象,直接回答:当 x 取何值时,一次函数的值大于反比例函数的值;
(3) 连接 AO、BO,求△ABO 的面积;
8、如图,已知 A(4,a) ,B(-2 ,-4)是一次函数 y=kx+b 的图象和反比例函数 的图象的交点.
(1)求反比例函数的解析式;(2) 求一次函数的解析式。
9、如图,一次函数 的图象与反比例函数 的图象交于A、B两点。
(1)利用图中条件求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值大于反比例函数的值的 的取值范围.
10、如图,在平面直角坐标系 xOy 中,反比例函数 ( )的图象与一次函数 的图象的一个
交点为 .
(1)求一次函数的解析式;
x
my =
bkxy +=
x
my =
x
4y x
= 0x > y x b= − +
(4 , )A m
(2)设一次函数 的图象与 y 轴交于点 B,P 为一次函数 的图象上一点,若 的
面积为 5,求点 P 的坐标.
11、已知 A(n,-2),B(1,4)是一次函数 y=kx+b 的图象和反比例函数 y= 的图象的两个交点,直线 AB 与 y 轴
交于点 C.
(1)求反比例函数和一次函数的关系式;
(2)求△AOC 的面积;
(3)求不等式 kx+b- <0 的解集(直接写出答案).
12、如图,将一块直角三角板 OAB 放在平面直角坐标系中,B(2,0),∠AOB=60°,点 A 在第一象限,过点 A
的双曲线为 .在 x 轴上取一点 P,过点 P 作直线 OA 的垂线 l,以直线 l 为对称轴,线段 OB 经轴对称变
换后的像是 O´B´.
(1)当点 O´与点 A 重合时,求点 P 的坐标.
(2)设 P(t,0),当 O´B´与双曲线有交点时,t 的取值范围是多少?
14、如图,一次函数 与反比例函数 的图像交于点A(4,m)和B(-8,-2),与y 轴交于点C,求:
(1) , ;
(2)根据函数图像可知,当 > 时,x 的取值范围是 ;
ky x
=
y x b= − + y x b= − + OBP△
x
m
x
m
2xky 11 +=
x
ky 2
2 =
=1k =2k
1y 2y
y
xD
C
B
A
O
P
y
x
6
6− O
A
B
A
B
C
P
Q
O x
y
(3)过点 A 作 轴于点 D,点 P 是反比例函数在第一象限图像上的一点,设直线 OP 与线段 AD 交
于点 E,当 时,求点 P 的坐标。
15、如图,反比例函数 的图像经过点 ,过点 作 轴于点B,△AOB的面积为 .
(1)求 和 的值;
(2)若一次函数 的图象经过点 ,求这个一次函数的解析式.
16、如图所示,一次函数 与反比例函数 的图象相交于 A,B 两点,且与坐标轴的交点
为 , ,点 B 的横坐标为-4.
(1)试确定反比例函数的解析式;
(2)求△AOB 的面积;
(3)直接写出不等式 的解.
17、如图,直线 分别交 轴, 轴于点 ,点 是直线 与双曲线 在第一象限内的交
点, 轴,垂足为点 , 的面积为 4.
(1)求点 的坐标;
(2)求双曲线的解析式及直线与双曲线另一交点 的坐标.
bxky 1 += )0x(x
ky 2 <=
)0,6(− )6,0(
x
kbxk 2
1 >+
1 12y x= + x y A C, P AC ky x
=
PB x⊥ B APB△
P
Q
xAD ⊥
1:3:SS ΔODE四边边形ODA
=
ky x
= ( )4,A b A AB x⊥ 2
k b
3y ax= − A
20.(2006)如图,已知反比例函数 y= (k<0)的图象经过点 A(- ,m),过点 A 作 AB⊥x 轴于点 B,且△AOB
的面积为 .
(1)求 k 和 m 的值;
(2)若一次函数 y=ax+1 的图象经过点 A,并且与 x 轴相交于点
C,求∠ACO 的度数和│AO│∶│AC│
(2008) 如图,已知反比例函数 y = 的图象经过点 A(1,- 3),一次函数 y = kx + b 的图象经过点 A 与点 C
(0,- 4),且与反比例函数的图象相交于另一点 B.
(1)试确定这两个函数的表达式;
(2)求点 B 的坐标.
(2011 绵阳)右图中曲线是反比例函数 的图象的一支.
(1)这个反比例函数图象的另一支位于哪个象限?常数 n 的取值范围是什么?
(2)若一次函数 的图象与反比例函数的图象交于点 A,与 x 轴交于点 B,△AOB 的面积为 2,
求 n 的值.
x
k 3
3
x
m
x
ny 7+=
3
4
3
2 +−= xy
A
BO x
y
第二讲:二次函数
一、y=ax2,y=ax2+c
二次函数 y=ax2 的图象的一些性质:
①、图象——“抛物线”是轴对称图形;
②、与 x、y 轴交点——( 0,0)即原点;(与 x、y 轴交点——( 0,c))
③、a 的绝对值越大抛物线开口越大,a﹥0,开口向上:
当 x﹤0 时,(对称轴左侧),y 随 x 的增大而减小(y 随 x 的减小而增大)
当 x﹥0 时,(对称轴右侧),y 随 x 的增大而增大(y 随 x 的减小而减小)
a﹤0,开口向下:
当 x﹤0 时,(对称轴左侧),y 随 x 的增大而增大(y 随 x 的减小而减小)
当 x﹥0 时,(对称轴右侧),y 随 x 的增大而减小(y 随 x 的减小而增大)
二、y=a(x-h)2,y=a(x-h)2+k
1、画 y=a(x-h)2+k(a≠0)的图像,列表时:在对称轴 x=h 两侧对称取点.
2、y=a(x-h)2+k(a≠0)具有以下性质:
抛物线 对称轴 顶点坐标 开口方向
y= a (x-h)2+k
(a>0)
x=h (h,k) 向上
y= a ( x-h)2+k
(a<0)
x=h (h,k) 向下
三、 y=ax2+bx+c(a、b、c 是常数 ,a≠0)
y=ax2+bx+c 化为 y=a (x+ )2+
,
对照 y=a(x-h)2+k 的形式得对称轴为 x=- ,顶点坐标为(- ,
)
关于二次函数变换:
1、比较函数 y=3x 2 与 y=3(x-1)2 的图象的性质.
2、在同一直角坐标系中比较函数 y=3(x-1)2 和 y=3(x-1)2+2 的图象性质
总结:
一般地,平移二次函数 y=ax2 的图象便可得到二次函数为 y=ax2+c,y=a(x-h)2,y=a(x-h)2+k 的图象.
(1)将 y=ax2 的 图象上下移动便可得到函数 y=ax2+c 的图象,当 c>0 时,向上移动,当 c<0 时,向下移动.
(2)将函数 y=ax2 的图象左右移动便可得到函数 y=a(x-h)2 的图象,当 h>0 时,向右移动,当 h<0 时,向左移
动.
(3)将函数 y=ax2 的图象既上下移,又左右移,便可得到函数 y=a(x-h)+k 的图象.
因此,这些函数的图象都是一条抛物线,它们的开口方向,对称轴和顶点坐标与 a,h,k 的值有关.
基础练习:
一、选择题
1、已知 + =y,其中 与 成反比例,且比例系数为 ,而 与 成正比例,且比例系数为 ,若 x=-1
时,y=0,则 , 的关系是( )
A. =0 B. =1 C. =0 D. =-1
a
b
2 a
bac
4
4 2−
a
b
2 a
b
2
a
bac
4
4 2−
1y 2y 1y 1
x 1k 2y 2x 2k
1k 2k
1 2k k+ 1 2k k 1 2k k− 1 2k k
2、已知二次函数 , 为常数,当 y 达到最小值时,x 的值为( )(A)
(A) ; (B) ; (C) ; (D)
3、若二次函数 的顶点在第一象限,且经过点(0,1),(-1,0), 则 S=a+b+c 的变化范围是
( )
(A)0
1; (C) 10,△>0; B.a>0, △<0; C.a<0, △<0; D.a<0, △<0
二、填空题:
5、已知方程组 的解也是二元一次方程 x-y=1 的一个解,则 a=_________。
6、已知直线 与 轴, 轴围成一个三角形,则这个三角形面积为 。
7、若 m<-1,则下列函数:① ;② y =-mx+1; ③ y = mx; ④ y =(m + 1)x 中,y 随 x 增大而增大
的是___________。
8、已知二次函数 (a≥1)的图像上两点 A、B 的横坐标分别是-1、2,点 O 是坐标原点,如果△AOB 是
直角三角形,则△OAB 的周长为 。
三、解答题:
9、已知不等式 的最小整数解是方程 的解,求 a 的值。
10、已知二次函数 y=x2+bx+c 的图像与 x 轴的两个交点的横坐标分别为 x1、x2,一元二次方程 x2+b2x+20=
0 的两实根为 x3、x4,且 x2-x3=x1-x4=3,求二次函数的解析式,并写出顶点坐标。
答案:
一、C B A B
二、 5、-
6、18
7、(1)(2)
8、
10、y=x2+3x+2 (-3/2,- 1/4)
巩固提高:
1、(陕西中考)若正比例函数的图像经过点(-1,2),则这个图像必经过点( )
A.(1,2) B.(-1,-2) C.(2,-1) D.(1,-2)
2
5 2 3
x ay
x y
+ =
− =
5
2
222 )(22 baxbaxy +++−= ba,
ba +
2
ba +
ab2−
2
ba −
2 +y ax bx c= +
2y ax=
6+= xy x y
( )0xx
my =
2y ax=
5( 2) 8 6( 1) 7x x− + < − + 2 4x ax− =
5224 +
2、(安徽中考)已知函数 的图象如图,则 的图象可能是( )
3、(黄冈中考)小高从家门口骑车去单位上班,先走平路到达点 A,再走上坡路到达点 B,最后走下坡路到达工
作单位,所用的时间与路程的关系如图所示.下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速
度分别保持和去上班时一致,那么他从单位到家门口需要的时间是( )
A.12 分钟 B.15 分钟 C.25 分钟 D.27 分钟
4、(广东深圳)如图,反比例函数 的图象与直线 的交点为 A,B,过点 A 作 y 轴的平行线与过点 B
作 x 轴的平行线相交于点 C,则 的面积为( )
A.8 B.6 C.4 D.2
5、(广西河池)如图 5,A、B 是函数 的图象上关于原点对称的任意两点,BC∥ 轴,AC∥ 轴,△ABC 的
面积记为 ,则( )
A. B. C. D.
6、函数 在同一直角坐标系内的图象大致是 ( )
7、已知二次函数 y=ax2+bx+c(a≠0)的图象如图 2 所示,给出以下结论:① a+b+c<0;② a-b+c<0;③ b+2a
<0;④ abc>0 .其中所有正确结论的序号是( )
A. ③④ B. ②③ C. ①④ D. ①②③
2y x
= x y
S
2S = 4S = 2 4S< < 4S >
2 +y ax b y ax bx c= + = +与
y kx b= + 2y kx b= +
4y x
= − 1
3y x= −
ABC△
A
O
BC x
y
第 4 题图
O
B
x
y
C
A
图 5
图
图
x-1 1
y
O
图 2
8、二次函数 y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:
①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),
其中正确结论的个数是( )
A. 4 个 B. 3 个 C. 2 个 D. 1 个
考点: 二次函数图象与系数的关系.
分析: 利用二次函数图象的相关知识与函数系数的联系,需要根据图形,逐一判断.
解答: 解:∵抛物线和 x 轴有两个交点,
∴b2﹣4ac>0,
∴4ac﹣b2<0,∴①正确;
∵对称轴是直线 x﹣1,和 x 轴的一个交点在点(0,0)和点(1,0)之间,
∴抛物线和 x 轴的另一个交点在(﹣3,0)和(﹣2,0)之间,
∴把(﹣2,0)代入抛物线得:y=4a﹣2b+c>0,
∴4a+c>2b,∴②错误;
∵把(1,0)代入抛物线得:y=a+b+c<0∴2a+2b+2c<0,∵b=2a,∴3b,2c<0,∴③正确;
∵抛物线的对称轴是直线 x=﹣1,∴y=a﹣b+c 的值最大,
即把(m,0)(m≠0)代入得:y=am2+bm+c<a﹣b+c,
∴am2+bm+b<a,即 m(am+b)+b<a,∴④正确;即正确的有 3 个,
9、已知二次函数 y=ax2+bx+c(a≠0)的图象如图,且关于 x 的一元二次方程 ax2+bx+c﹣m=0 没有实数根,有下
列结论:
①b2﹣4ac>0;②abc<0;③m>2.
其中,正确结论的个数是( )
A. 0 B. 1 C. 2 D. 3
解答: 解:①∵二次函数 y=ax2+bx+c 与 x 轴有两个交点,
∴b2﹣4ac>0,故①正确;
②∵抛物线的开口向下,∴a<0,∵抛物线与 y 轴交于正半轴,∴c>0,∵对称轴 x=﹣ >0,
∴ab<0,∵a<0,∴b>0,∴abc<0,故②正确;
③∵一元二次方程 ax2+bx+c﹣m=0 没有实数根,
∴y=ax2+bx+c 和 y=m 没有交点,由图可得,m>2,故③正确.故选 D.
10、当﹣2≤x≤1 时,二次函数 y=﹣(x﹣m)2+m2+1 有最大值 4,则实数 m 的值为( )
A. B. 或 C. 2 或 D. 2 或﹣ 或
解答:解:二次函数的对称轴为直线 x=m,
①m<﹣2 时,x=﹣2 时二次函数有最大值,
11、抛物线
y=ax2+bx+c 的
顶点为 D(﹣1,2),与 x 轴的一个交点 A 在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:
①b2﹣4ac<0;②a+b+c<0;③c﹣a=2;④方程 ax2+bx+c﹣2=0 有两个相等的实数根.
其中正确结论的个数为( C )
A、1 个 B、2 个 C、3 个 D、4 个
12、(钦州中考)一次函数的图象过点(0,2),且函数 y 的值随自变量 x 的增大而增大,请写出一个符合条件
的函数解析式:_ _.
13、(绍兴中考)如图,已知函数 和 的图象交点为 ,
则不等式 的解集为 .
14、(湖北黄石)如图所示,P1(x1,y1)、P2(x2,y2),……Pn(xn,yn)在函数 y= (x>0)的图象上,△
OP1A1,△P2A1A2,△P3A2A3……△PnAn-1An……都是等腰直角三角形,斜边 OA1,A1A2……An-1An,都在 x 轴上,
则 y1+y2+…yn= 。
15.(天津市)已知图中的曲线是反比例函数 ( 为常数)图象的一支.
(Ⅰ) 这个反比例函数图象的另一支在第几象限?常数 的取值范围是什么?
(Ⅱ)若该函数的图象与正比例函数 的图象在第一象内限的交点为 ,过 点作 轴的垂线,垂足为
,当 的面积为 4 时,求点 的坐标及反比例函数的解析式.
此时﹣(﹣2﹣m)2+m2+1=4,
解得 m=﹣,与 m<﹣2 矛盾,故 m 值不存在;
②当﹣2≤m≤1 时,x=m 时,二次函数有最大值,
此时,m2+1=4,解得 m=﹣ ,m= (舍去);
③当 m>1 时,x=1 时,二次函数有最大值,
此时,﹣(1﹣m)2+m2+1=4,解得 m=2,
综上所述,m 的值为 2 或﹣ .故选 C.
y x b= + 3y ax= + P
3x b ax+ > +
O x
y
1
P
y=x+b
y=ax+3
x
9
5my x
−= m
m
2y x= A A x
B OAB△ A
x
y
O
第 14 题
图
16、(浙江嘉兴)如图,曲线 C 是函数 在第一象限内的图象,抛物线是函数 的图象.点
( )在曲线 C 上,且 都是整数.
(1)求出所有的点 ;
(2)在 中任取两点作直线,求所有不同直线的条数;
(3)从(2)的所有直线中任取一条直线,求所取直线与抛物线有公共点的概率.
17.某商店经销一种销售成本为每千克 40 元的水产品.据市场分析,若按每千克 50 元销售,一个月能售出 500kg;
销售单价每涨 1 元,月销售量就减少 10kg.针对这种水产品的销售情况,请解答以下问题:
(1)当销售单价定为每千克 55 元时,计算月销售量和月销售利润;
(2)设销售单价为每千克 x 元,月销售利润为 y 元,求 y 与 x 的函数关系式;
(3)商店想在月销售成本不超过 10000 元的情况下,使得月销售利润达到 8000 元,销售单价应定为多少?
31, 解:(1) 按每千克 50 元销售,一个月能售出 500kg,销售单价每涨 1 元,月销售量就减少 10kg。现在单价
定为每千克 55 元,即涨了 5 元,所以月销售量减少 50kg,所以月销售量为 500-50=450kg,月销售利润为
(55-40)×450=6750 元。
(2) 设销售单价为每千克 x 元,则上涨了 x-50 元,月销售量减少(x-50)×10kg,即月销售量为 500-10
(x-50),所以利润为 y=[500-10(x-50)] ×(x-40),
即
(3)月销售利润达到 8000 元,即 ,解得 x=60 或 x=80
当 x=60 时,销售量为 500-10(60-50)=400,
当 x=80 时,销售量为 500-10(80-50)=200
而月销售量不超过 10000 元,即销售量不超过 ,而 400>250,所以 x=60 应舍去,所以销售单价应
定于 80 元。
18、(重庆市江津区)抛物线 与 x 轴交与 A(1,0),B(- 3,0)两点,
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交 y 轴与 C 点,在该抛物线的对称轴上是否存在点 Q,使得△QAC 的周长最小?若存
在,求出 Q 点的坐标;若不存在,请说明理由.
(3)在(1)中的抛物线上的第二象限上是否存在一点 P,使△PBC 的面积最大?,若存在,求出点 P 的坐标
xy 6= 422 +−−= xxy
),( yxPn
nP
210( 140 4000)y x x= − + −
28000 10( 140 4000)x x= − + −
10000 25040
=
cbxxy ++−= 2
1 2n = ,, x y,
( )nP x y,
(第 12 题)
6
4
2
2 4 6
y
xO
及△PBC 的面积最大值.若没有,请说明理由.
19、(湖北省荆门市) 一开口向上的抛物线与 x 轴交于 A( ,0),B(m+2,0)两点,记抛物线顶点为
C,且 AC⊥BC.
(1)若 m 为常数,求抛物线的解析式;
(2)若 m 为小于 0 的常数,那么(1)中的抛物线经过怎么样的平移可以使顶点在坐标原点?
(3)设抛物线交 y 轴正半轴于 D 点,问是否存在实数 m,使得△BCD 为等腰三角形?若存在,求出 m 的值;
若不存在,请说明理由.
20.已知经过原点的抛物线 y=-2x2+4x(如图所示)与 x 的另一交点为 A 现将它向右平移 m(m>0)位,所得抛
物线与 x 轴交于 C、D 点,与原抛物线交于点 P
(1)求点 P 的坐标(可用含 m 式子表示)
(2)设△PCD 的面积为 s,求 s 关于 m 关系式.
(3)过点 P 作 x 轴的平行线交原抛物线于点 E,交平移后的抛物线于点 F.请问是否存在 m,使以点 E、O、A、
F 为顶点的四边形为平行四边形.若存在,求出 m 的值,若不存在,请说明理由.
考点:二次函数综合题.
分析:(1)首先将抛物线表示出顶点式的形式,再进行平移,左加右减,即可得出答案;
(2)求出抛物线与 x 轴的交点坐标,根据当 0<m<2,当 m=2,即点 P 在 x 轴时,当 m>2 即点 P 在第四象限时,
分别得出即可;
(3)根据 E、O、A、F 为顶点的四边形是平行四边形,则 EF=OA=2 由轴对称可知 PE=PF,表示出 E 点的坐标,
再把点 E 代入抛物线解析式得出即可.
解答: 解:
2m −
O BA
C
D
x
y
第 15 题图
(1)原抛物线:y=-2x2+4x=-2(x-1)2+2,
则平移后的抛物线为:y=-2(x-1-m)2+2,
由题得 ,
解得 ,
∴点 P 的坐标为( , );
(2)抛物线:y=-2x2+4x=-2x(x-2)
∴抛物线与 x 轴的交点为 O(0,0)A(2,0),
∴AC=2,
∵C、D 两点是抛物线 y=-2x2+4x 向右平移 m(m>0)个,
单位所得抛物线与 x 轴的交点∴CD=OA=2,
①当 0<m<2,即点 P 在第一象限时,如图 1,作 PH⊥x 轴于 H.
∵P 的坐标为( , ),
∴PH= ,
∴S= CD•2•(- m2+2)=- m2+2,
②当 m=2,即点 P 在 x 轴时,△PCD 不存在,
③当 m>2 即点 P 在第四象限时,如图 2,作 PH⊥x 轴于 H.
∵P 的坐标为( , ),
∴PH= ,
∴S= CD•HP= ×2× = m2-2;
(3)如图 3 若以 E、O、A、F 为顶点的四边形是平行四边形,则 EF=OA=2
由轴对称可知 PE=PF,
∴PE= ,
∵P( , ),
∴点 E 的坐标为( , ),
把点 E 代入抛物线解析式得: ,
第三讲:二次函数应用
一、动点问题
(一)、因动点产生的面积关系
例 1、在平面直角坐标系中,△BCD 的边长为 3cm 的等边三角形, 动点 P、Q 同时从点 A、O 两点出发,分别沿
AO、OB 方向匀速移动,它们的速度都是 1cm/s, 当点 P 到达点 O 时,P、Q 两点停止运动. 设点 P 的运动时间为 t(s),
解答下列问题:
(1) 求 OA 所在直线的解析式;
(2) 当 t 为何值时, △POQ 是直角三角形;
(3) 是否存在某一时刻 t,使四边形 APQB 的面积是△AOB 面积的三分之二? 若存
在, 求出相应的 t 值; 若不存在,请说明理由.
解:⑴ 根据题意:AP=t cm,BQ=t cm.
△ABC 中,AB=BC=3cm,∠B=60°,
∴BP=(3-t ) cm.
△PBQ 中,BP=3-t,BQ=t,
若△PBQ 是直角三角形,则∠BQP=90°或∠BPQ=90°.
当∠BQP=90°时,BQ= BP.
即 t= (3-t ),
t=1 (秒).
当∠BPQ=90°时,BP= BQ.
3-t= t,
t=2 (秒).
答:当 t=1 秒或 t=2 秒时,△PBQ 是直角三角形. …………………4′
⑵ 过 P 作 PM⊥BC 于 M .Rt△BPM 中,sin∠B= ,
1
2
1
2
1
2
1
2
PM
PB
Q
P
P
A
x
y
BO
∴PM=PB·sin∠B= (3-t ).
∴S△PBQ= BQ·PM= · t · (3-t ).
∴y=S△ABC-S△PBQ
= ×32× - · t · (3-t )
= .
∴y 与 t 的关系式为: y= . …………………6′
假设存在某一时刻 t,使得四边形 APQC 的面积是△ABC 面积的 ,
则 S 四边形 APQC= S△ABC .
∴ = × ×32× .
∴t 2-3 t+3=0.
∵(-3) 2-4×1×3<0,
∴方程无解.
∴无论 t 取何值,四边形 APQC 的面积都不可能是△ABC 面积的
.……8′
例 2、 如图,边长为 1 的正方形 OABC 的顶点 O 为坐标原点,点 A 在 x 轴的正半轴上,点 C 在 y 轴的正半轴
上.动点 D 在线段 BC 上移动(不与 B,C 重合),连接 OD,过点 D 作 DE⊥OD,交边 AB 于点 E,连接 OE.记 CD
的长为 t.
(1) 当 t= 时,求直线 DE 的函数表达式;
(2) 如果记梯形 COEB 的面积为 S,那么是否存在 S 的最大值?若存在,请求出这个最大值及此时 t 的值;
若不存在,请说明理由;
解:(1)易知△CDO∽△BED,
所以 ,即 ,得 BE= ,则点 E
的坐标为 E(1, ).……………………………(2 分)
设直线 DE 的一次函数表达式为 y=kx+b ,直线经过两点 D( ,1) 和E(1 , ) ,
代 入 y=kx+b 得 , ,故 所 求 直 线 DE 的 函 数 表 达 式 为 y=
.…………………………(2 分)
3
2
1
2
1
2
3
2
1
2
3
2
1
2
3
2
23 3 3 9 3
4 4 4
t t− +
23 3 3 9 3
4 4 4
t t− +
2
3
2
3
23 3 3 9 3
4 4 4
t t− + 2
3
1
2
3
2
2
3
3
1
BD
CO
BE
CD =
3
11
13
1
−
=
BE 9
2
9
7
3
1
9
7
3
1−=k 9
10=b
9
10
3
1 +− x
M
A
CQB
P
(注:用其它三角形相似的方法求函数表达式,参照上述解法给分)
(2) 存在 S 的最大值.………………………………………………1 分
求最大值:易知△COD∽△BDE,所以 ,即 ,BE=t-t2,……1 分
×1×(1+t-t2) .………………………1 分
故当 t= 时,S 有最大值 .……………………………2 分
(二)因动直线产生的面积关系
例 3.如图所示,已知抛物线 y=x2+bx+c 经过点(1,-5)和(-2,4).
(1)求这条抛物线的解析式.
(2)设此抛物线与直线 y=x 相交于点 A,B(点 B 在点 A 的右侧),平行于 x轴的直线 x=m(00,-y 表示点 E 到 OA 的距离.
∵OA 是 的对角线,
∴ .
因为抛物线与 轴的两个交点是(1,0)的(6,0),所以,自变量 的
取值范围是 1< <6.
① 根据题意,当 S = 24 时,即 .
化简,得 解之,得
故所求的点 E 有两个,分别为 E1(3,-4),E2(4,-4).
点 E1(3,-4)满足 OE = AE,所以 是菱形;
7
2x =
x y
x x
7
2x =
27( )2y a x k= − +
2
2
7(6 ) 0,2
7(0 ) 4.2
a k
a k
− + =
− + =
2 25, .3 6a k= = −
22 7 25( )3 2 6y x= − − 7 25( , ).2 6
−
( , )E x y
22 7 25( )3 2 6y x= − −
OEAF
21 72 2 6 4( ) 252 2OAES S OA y y= = × × ⋅ = − = − − +
x x
x
274( ) 25 242x− − + =
27 1( ) .2 4x − = 1 23, 4.x x= =
OEAF
7
2x =
B(0,4)
A(6,0)
E
F
x
y
O
点 E2(4,-4)不满足 OE = AE,所以 不是菱形.
② 当 OA⊥EF,且 OA = EF 时, 是正方形,此时点 E 的
坐标只能是(3,-3).
而坐标为(3,-3)的点不在抛物线上,故不存在这样的点 E,
使 为正方形.
例 5. 如图所示, 在平面直角坐标系 xOy 中, 矩形 OABC 的边长 OA、OC 的长分剔为 12cm、6 cm, 点 A、C 分别在 y
轴的负半轴和 x 轴的正半轴上, 抛物线 y=ax2+bx+c 经过点 A、B, 且 18a+c=0.
(1)求抛物线的解析式;
(2)如果点 P 由点 A 开始沿 AB 边以 1cm/s 的速度向点 B 移动, 同时点 Q 由点 B 开始沿 BC 边以 2cm/s 的速
度向点 C 移动.
①移动开始后第 t 秒时, 设△PBQ 的面积为 S, 试写出 S 与 t 之间的函数关系式, 并写出 t 的取值范围;
②当 S 取得最小值时, 在抛物线上是否存在点 R, 使得以 P、B、Q、R 为顶点的四边形是平行四边形? 如果
存在, 求出 R 点的坐标, 如果不存在, 请说明理由.
解: (1)据题意知: A(0, -12), B(6, -12)
∵A 点在抛物线上, ∴C=-12
∵18a+c=0, ∴a= ………(1 分)
由 AB=6 知抛物线的对称轴为: x=3
即:
∴抛物线的解析式为: …(3 分)
(2)①由图象知: PB=6-t, BQ=2t
∴S== ……(4 分)
即 (0≤t≤1) ………………(5 分)
②假设存在点 R, 可构成以 P、B、R、Q 为顶点的平行四边形.
∵ (0≤t≤1)
∴当 t= 时, S 取得最小值 9. ………………………………………(6 分)
这时 PB=6-3=3, BQ=6, P(3, -12), Q(6, -6) ………(7 分)
分情况讨论:
A】假设 R 在 BQ 的右边, 这时 QR PB, ∵P(3, -12),PB=3, Q(6, -6)
R 的横坐标为 9, R 的纵坐标为-6, 即(9, -6)
代入 , 左右两边不相等
∴这时 R(9, -6) 不在抛物线上. ……………………………………(8 分)
B】假设 R 在 BQ 的左边, 这时 PR QB, 则:
R 的横坐标为 3, 纵坐标为-6, 即(3, -6)
代入 , 左右两边不相等, R 不在抛物线上. …………(9 分)
C】假设 R 在 PB 的下方, 这时 PR QB, 则:
R(6, -18)代入 , 左右两边相等, R(6, -18)在抛物线上.
综上所述, 存点一点 R(6, -18)满足题意. …………………………(10 分)
同步练习
OEAF
OEAF
OEAF
3
2
432
−=⇒=− ba
b
1243
2 2 −−= xxy
ttttBQPB 62)6(2
1
2
1 2 +−=⋅−=⋅
tts 62 +−=
9)3(6 22 +−−=+−= ttts
3
1243
2 2 −−= xxy
1243
2 2 −−= xxy
1243
2 2 −−= xxy
Q
P
C
A
x
y
B
O
1、已知抛物线 与 轴相交于 两点( 点在 点的左边),与 轴的负半轴相交于点 ,
(1)求抛物线的解析式;
(2)在抛物线上是否存在点 ,使 ?如果存在,请确定点 的位置,并求出点 的坐标:
如果不存在,请说明理由.
2、如图,抛物线 与 轴交于点 、B 两点,抛物线的对称
轴为直线 x=1,
(1)求 的值及抛物线的解析式;
(2) 过 A 的直线与抛物线的另一交点 C 的横坐标为 2. 直线 AC 的解析式;
(3)点 Q 是抛物线上的一个动点, 在 x 轴上是否存在点 F ,使得以点 A、C、F、
Q 为顶点四边形是平行四边形?若存在,请求出所有满足条件的点 F 的坐标;
若不存在,请说明理由.
3、如图,已知二次函数 的图象与 轴交于点 ,点 ,与
轴 交 于 点 , 其 顶 点 为 , 直 线 的 函 数 关 系 式 为 , 又
.
(1)求二次函数的解析式和直线 的函数关系式;
(2)抛物线上是否存在一点 P,使△PBC 以 BC 为直角边的直角三角形?若存,
求出点 P 的坐标;若不存在,说明理由.
4、如图,在平面直角坐标系 xOy 中,抛物线的对称轴为直线 x=2, 该抛物线与 x 轴交干 A、B 两点(B 在 A 的
右侧), 与 y 轴交于点 C, 且 B、C 的坐标分别为(3,0)、(0,3).
2 4y x x m= − + x A B, B A y C
6AB =
P AOP COP△ ≌△ P P
63)1(2 −−−−= mxmxy x A
m
2 2 3y ax ax= − + x A B y
C D DC 3y kx= +
tan 1OBC∠ =
DC
y
x
D
C
A O B
Q C
A x
y
BO
B O x
y
A
A
C
(1)求此抛物线的解析式;
(2)抛物线上是否存在一点 P,使△PAC 是直角三角形?若存在,求出点 P 的坐标;若不存在,请说明理
由.
(三)、因动点产生的三角形相似问题
例 6.如图,直线 与 轴, 轴分别相交于点 ,点 ,经过 两
点的抛物线 与 轴的另一交点为 ,顶点为 ,且对称轴是直线
.
(1)求 点的坐标;
(2)求该抛物线的函数表达式;
(3)连结 .请问在 轴上是否存在点 ,使得以点 为顶点的三角
形与 相似,若存在,请求出点 的坐标;若不存在,请说明理由.
解:(1) 直线 与 轴相交于点 ,
当 时, ,
点 的坐标为 .…………………………(1 分)
又 抛物线过 轴上的 两点,且对称轴为 ,
根据抛物线的对称性,
点 的坐标为 .…………………………(2 分)
(2) 过点 ,易知 , .-----(3 分)
3y x= − + x y B C B C,
2y ax bx c= + + x A P
2x =
A
AC x Q P B Q, ,
ABC△ Q
3y x= − + x B
∴ 0y = 3x =
∴ B (3 0),
x A B, 2x =
∴ A (1 0),
3y x= − + C (0 3)C , 3c∴ =
y
xO B
C
A
A
A B
C
P
O x
y
2x =
A B
C
P
O x
y
2x =
1Q 2QM
又 抛物线 过点 ,
∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙(4 分)
解,得 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙(5 分)
. ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙(6 分)
(3)连结 ,由 ,得 ,
设抛物线的对称轴交 轴于点 ,在 中, ,
.
由点 易得 ,在等腰直角三角形 中, ,
由勾股定理,得 .∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙(7 分)
假设在 轴上存在点 ,使得以点 为顶点的三角形与 相似.
①当 , 时, .
即 , ,
又 , 点 与点 重合, 的坐标是 . ∙∙∙∙∙∙∙∙∙∙(9 分)
②当 , 时, .
即 , .
,
的坐标是 .∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙(11 分)
.
点 不可能在 点右侧的 轴上(无此判断,亦不扣分).
综上所述,在 轴上存在两点 ,能使得以点 为顶点的三角形与 相似.(12
分)
同步练习
1、如图,在直角坐标系中, 为原点,抛物线 与 轴的负半轴交于点 ,与 轴的正半轴交
2y ax bx c= + + (1 0) (3 0)A B,, ,
3 0
9 3 3 0
a b
a b
+ = =∴ + + =
,
.
1
4
a
b
=
= −
,
.
2 4 3y x x∴ = − +
PB 2 24 3 ( 2) 1y x x x= − + = − − (2 1)P −,
x M Rt PBM△ 1PM MB= =
45 2PBM PB∴ = =,∠
(3 0) (0 3)B C,, , 3OB OC= = OBC 45ABC = ∠
3 2BC =
x Q P B Q, , ABC△
BQ PB
BC AB
= 45PBQ ABC= = ∠ ∠ PBQ ABC△ ∽△
2
23 2
BQ = 3BQ∴ =
3BO = ∴ Q O 1Q∴ (0 0),
QB PB
AB BC
= 45QBP ABC= = ∠ ∠ QBP ABC△ ∽△
2
2 3 2
QB = 2
3QB∴ =
2 73 3 3 3OB OQ OB QB= ∴ = − = − = ,
2Q∴ 7 03
,
180 45 135 135PBx BAC PBx BAC= − = < ∴ ≠ , ,∠ ∠ ∠ ∠
∴ Q B x
x 1 2
7(0 0) 03Q Q
,, , P B Q, , ABC△
O 2 3y x bx= + + x A y
于点 B,tan∠ACO= .
(1)求抛物线的解析式;
(2)若直线 与线段 交于点 (不与点 重合),则是否存在这样的直线 ,使得以
为顶点的三角形与 相似?若存在,求出该直线的函数表达式
及点 的坐标;若不存在,请说明理由.
(五)、其它二次函数的综合问题
例 7、如图,一元二次方程 的二根 ( )是抛物线 与 轴的两个交
点 的横坐标,且此抛物线过点 .
(1)求此二次函数的解析式.
(2)设此抛物线的顶点为 ,对称轴与线段 相交于点 ,求点 和点 的坐标.
(3)在 轴上有一动点 ,当 取得最小值时,求 点的坐标.
解:(1)解方程
得 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙1 分
抛物线与 轴的两个交点坐标为: ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2 分
设抛物线的解析式为
∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3 分
在抛物线上
∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4 分
抛物线解析式为: ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙5 分
(2)由 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6 分
抛物线顶点 的坐标为: ,对称轴方程为: ∙∙∙∙∙∙∙∙∙∙∙7 分
3
1
: ( 0)l y kx k= ≠ BC D B C, l
B O D, , BAC△
D
2 2 3 0x x+ − = 1 2x x, 1 2x x< 2y ax bx c= + + x
B C, (3 6)A ,
P AC Q P Q
x M MQ MA+ M
2 2 3 0x x+ − =
1 23 1x x= − =,
∴ x ( 3 0) (1 0)C B− ,, ,
( 3)( 1)y a x x= + −
(3 6)A∵ ,
6 (3 3) (3 1)a= + −∴ · 1
2a =∴
∴ 21 3
2 2y x x= + −
2 21 3 1 ( 1) 22 2 2y x x x= + − = + −
∴ P ( 1 2)− −, 1x = −
A
O
B
C
x
y
x
y
A(3,6)
Q
C O B
P
设直线 的方程为:
在该直线上
解得 直线 的方程为: ∙∙∙∙∙∙∙∙∙∙∙∙∙9 分
将 代入 得
点坐标为 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10 分
(3)作 关于 轴的对称点 ,连接 ; 与 轴交于点 即为所求的点
∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙11 分
设直线 方程为
解得
直线 : ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙12 分
令 ,则 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙13 分
点坐标为 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙14 分
同步练习
1、如图所示,在平面直角坐标系中,抛物线 经过点 A(3,0)、B(5,0)、C(0,5)三点.
(1)求该抛物线的函数表达式;
(2)设抛物线的顶点为 D,求△BCD 的面积;
(3)在抛物线的对称轴上有一个动点 P,当△0CP 是腰长为 5 的等腰三角形时,
求点 P 的坐标.
AC y kx b= +
(3 6) ( 3 0)A C −∵ ,, ,
3 6
3 0
k b
k b
+ =
− + =
∴ 3
1
b
k
=
=
∴ AC 3y x= +
1x = − 3y x= + 2y =
Q∴ ( 1 2)− ,
A x (3 6)A′ −, A Q′ A Q′ x M
A Q′ y kx b= +
3 6
2
k b
k b
+ = −
− + =
∴ 0
2
b
k
=
= −
∴ A C′ 2y x= −
0x = 0y =
M∴ (0 0),
2y ax bx c= + +
x
y
A(3,6)
Q
C O B
P
(3 6)A −,
AO B
C
x
y
2、如图,已知抛物线 与 x 轴的一个交点 A(3,0).
(1)分别求出这条抛物线与 x 轴的另一个交点 B 及与 y 轴的交点 C 的坐标;
(2)设抛物线的顶点为 D,求直线 CD 的解析式;
(3)求 tan∠DAC 的值.
32 ++−= mxxy
x1 2 3 4-1-2
-1
-2
-3
1
2
3
y
O
A
C
D
B