2008年福建省厦门市高中阶段各类学校招生考试题及答案

2008年福建省厦门市高中阶段各类学校招生考试题及答案

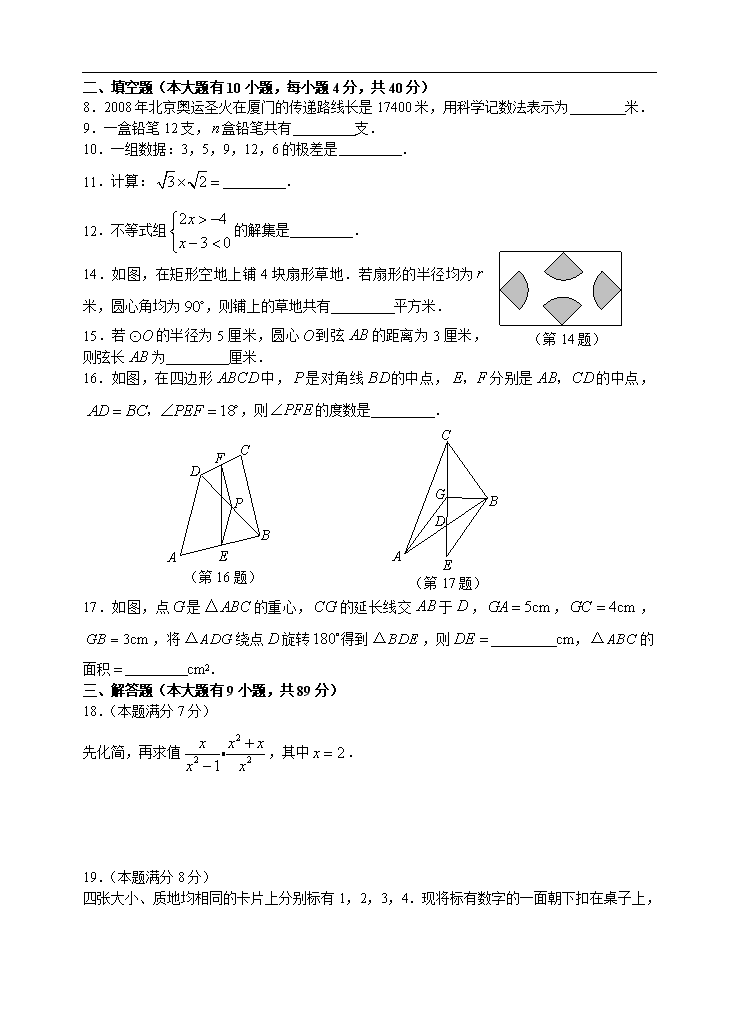
福建省厦门市2008年初中毕业及高中阶段各类学校招生考试 数 学 试 题 ‎（试卷满分：150分 考试时间：120分钟）‎ 考生注意：本学科考试有两张试卷，分别是本试题（共4页26题）和答题卡．试题答案要填在答题卡相应的答题栏内，否则不能得分．‎ 一、选择题（本大题有7题，每小题3分，共21分．每小题有四个选 项，其中有且只有一个选项正确）‎ ‎1．下面几个数中，属于正数的是（ ）‎ 正面 ‎（第2题）‎ A．3 B． C． D．‎ ‎2．由四个相同的小正方体堆成的物体如图所示，它的俯视图是（ ）‎ A．‎ B．‎ C．‎ D．‎ ‎3．某鞋店试销一种新款女鞋，销售情况如下表所示：‎ 型号 ‎22‎ ‎22.5‎ ‎23‎ ‎23.5‎ ‎24‎ ‎24.5‎ ‎25‎ 数量（双）‎ ‎3‎ ‎5‎ ‎10‎ ‎15‎ ‎8‎ ‎3‎ ‎2‎ 鞋店经理最关心的是，哪种型号的鞋销量最大．对他来说，下列统计量中最重要的是（ ）‎ A．平均数 B．众数 C．中位数 D．方差 ‎4．已知方程，那么方程的解是（ ）‎ A． B． C． D．‎ ‎5．下列函数中，自变量的取值范围是的函数是（ ）‎ A． B． C． D．‎ ‎6．在平行四边形中，，那么下列各式中，不能成立的是（ ）‎ A． B． C． D．‎ ‎7．在四川抗震救灾中，某抢险地段需实行爆破．操作人员点燃导火线后，要在炸药爆炸前跑到400米以外的安全区域．已知导火线的燃烧速度是1.2厘米/秒，操作人员跑步的速度是5米/秒．为了保证操作人员的安全，导火线的长度要超过（ ）‎ A．66厘米 B．76厘米 C．86厘米 D．96厘米 二、填空题（本大题有10小题，每小题4分，共40分）‎ ‎8．2008年北京奥运圣火在厦门的传递路线长是17400米，用科学记数法表示为 米．‎ ‎9．一盒铅笔12支，盒铅笔共有 支．‎ ‎10．一组数据：3，5，9，12，6的极差是 ．‎ ‎11．计算： ．‎ ‎（第14题）‎ ‎12．不等式组的解集是 ．‎ ‎14．如图，在矩形空地上铺4块扇形草地．若扇形的半径均为米，圆心角均为，则铺上的草地共有 平方米．‎ ‎15．若的半径为5厘米，圆心到弦的距离为3厘米，则弦长为 厘米．‎ A B E G C D ‎（第17题）‎ ‎16．如图，在四边形中，是对角线的中点，分别是的中点，，则的度数是 ．‎ C F D B E A P ‎（第16题）‎ ‎17．如图，点是的重心，的延长线交于，，，，将绕点旋转得到，则 cm，的面积 cm2．‎ 三、解答题（本大题有9小题，共89分）‎ ‎18．（本题满分7分）‎ 先化简，再求值，其中．‎ ‎19．（本题满分8分）‎ 四张大小、质地均相同的卡片上分别标有1，2，3，4．现将标有数字的一面朝下扣在桌子上，然后由小明从中随机抽取一张（不放回），再从剩下的3张中随机取第二张．‎ ‎（1）用画树状图的方法，列出小明前后两次取得的卡片上所标数字的所有可能情况；‎ ‎（2）求取得的两张卡片上的数字之积为奇数的概率．‎ ‎20．（本题满分9分）‎ 如图，为了测量电线杆的高度，在离电线杆25米的处，用高1.20米的测角仪测得电线杆顶端的仰角，求电线杆的高．（精确到0.1米）‎ 参考数据：，，，．‎ A B E C D ‎（第20题）‎ ‎21．（本题满分9分）‎ 某商店购进一种商品，单价30元．试销中发现这种商品每天的销售量（件）与每件的销售价（元）满足关系：．若商店每天销售这种商品要获得200元的利润，那么每件商品的售价应定为多少元？每天要售出这种商品多少件？‎ ‎22．（本题满分10分）‎ 已知一次函数与反比例函数的图象交于点和．‎ ‎（1）求反比例函数的关系式；‎ ‎（2）求点的坐标；‎ ‎（3）在同一直角坐标系中画出这两个函数图象的示意图，并观察图象回答：当为何值时，一次函数的值大于反比例函数的值？‎ ‎23．（本题满分10分）‎ 已知：如图，中，，以为直径的交于点，于点．‎ C P B O A D ‎（第23题）‎ ‎（1）求证：是的切线；‎ ‎（2）若，求的值．‎ ‎24．（本题满分12分）‎ 已知：抛物线经过点．‎ ‎（1）求的值；‎ ‎（2）若，求这条抛物线的顶点坐标；‎ ‎（3）若，过点作直线轴，交轴于点，交抛物线于另一点，且，求这条抛物线所对应的二次函数关系式．（提示：请画示意图思考）‎ ‎25．（本题满分12分）‎ 已知：如图所示的一张矩形纸片（），将纸片折叠一次，使点与重合，再展开，折痕交边于，交边于，分别连结和．‎ ‎（1）求证：四边形是菱形；‎ ‎（2）若，的面积为，求的周长；‎ ‎（3）在线段上是否存在一点，使得？‎ A E D C F B ‎（第25题）‎ 若存在，请说明点的位置，并予以证明；若不存在，请说明理由．‎ ‎26．（本题满分12分）‎ 如图，在直角梯形中，，，点为坐标原点，点在 轴的正半轴上，对角线相交于点．，．‎ ‎（1）求和的值；‎ ‎（2）求直线所对应的函数关系式；‎ y x A B D M O ‎（第26题）‎ ‎（3）已知点在线段上（不与点重合），经过点和点的直线交梯形的边于点（异于点），设，梯形被夹在内的部分的面积为，求关于的函数关系式．‎ 福建省厦门市2008年初中毕业及高中阶段各类学校招生考试 数学试题参考答案及评分标准 一、选择题（本大题有7题，每小题3分，共21分）‎ ‎1．A 2．C 3．B 4．C 5．B 6．D 7．D 二、填空题（本大题有10小题，每小题4分，共40分）‎ ‎8． 9． 10．9 11． 12．‎ ‎13． 14． 15．8 16．18 17．2，18‎ 三、解答题（本大题有9小题，共89分）‎ ‎18．解：原式 4分 ‎ 6分 当时，原式． 7分 ‎19．解：（1）‎ ‎2 3 4‎ ‎1 3 4‎ ‎1 2 4‎ ‎1 2 3‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ 第一次 第二次 ‎ 6分 ‎（2）（积为奇数）． 8分 A B E C D ‎（第20题）‎ ‎20．解：在中，‎ ‎ 4分 ‎ 6分 ‎ 8分 ‎（米）‎ 答：电线杆的高度约为11.3米． 9分 ‎21．解：根据题意得： 4分 整理得： 6分 ‎（元） 7分 ‎（件） 8分 答：每件商品的售价应定为40元，每天要销售这种商品20件． 9分 P O Q x y ‎1‎ ‎2‎ ‎2‎ ‎1‎ ‎-1‎ ‎-2‎ ‎-2‎ ‎-1‎ ‎22．解：（1）设反比例函数关系式为，‎ 反比例函数图象经过点．‎ ‎． 2分 反比例函数关第式． 3分 ‎（2）点在上，‎ ‎． 5分 ‎． 6分 ‎（3）示意图． 8分 当或时，一次函数的值大于反比例函数的值． 10分 ‎23．（1）证明：，‎ ‎． 1分 又，‎ ‎ 2分 ‎． 3分 ‎ 4分 又于，，‎ ‎． 5分 是的切线． 6分 C P B O A D ‎（2）连结，是直径，‎ ‎， 8分 ‎，，‎ ‎． 9分 ‎． 10分 ‎24．解：（1）依题意得：， 2分 ‎． 3分 ‎（2）当时，， 4分 抛物线的顶点坐标是． 6分 y x O B P A ‎（3）当时，抛物线对称轴，‎ 对称轴在点的左侧．‎ 因为抛物线是轴对称图形，且．‎ ‎ 9分 ‎．‎ ‎． 10分 又，． 11分 抛物线所对应的二次函数关系式． 12分 解法2：（3）当时，，‎ 对称轴在点的左侧．因为抛物线是轴对称图形，‎ ‎，且 9分 ‎． 10分 又，解得： 11分 这条抛物线对应的二次函数关系式是． 12分 解法3：（3），，‎ ‎ 7分 轴， 8分 即：．‎ 解得：，即 10分 由，．‎ ‎ 11分 这条抛物线对应的二次函数关系式 12分 ‎25．解：（1）连结交于，‎ A E D C F B P O 当顶点与重合时，折痕垂直平分，‎ ‎， 1分 在平行四边形中，，‎ ‎，‎ ‎．‎ ‎ 2分 四边形是菱形． 3分 ‎（2）四边形是菱形，．‎ 设，，，‎ ‎ 4分 ‎ ①‎ 又，则． ② 5分 由①、②得： 6分 ‎，（不合题意舍去）‎ 的周长为． 7分 ‎（3）过作交于，则就是所求的点． 9分 证明：由作法，，‎ 由（1）得：，又，‎ ‎，‎ ‎，则 10分 ‎ 四边形是菱形，，． 11分 ‎ 12分 ‎26．解：（1）， 2分 ‎ ‎，， 3分 ‎ ‎（2）由（1）得：，．‎ ‎，易证 4分 ‎，． 5分 过的直线所对应的函数关系式是． 6分 ‎（3）依题意：当时，在边上，‎ 分别过作，，垂足分别为和，‎ y x A B D M O N F E ‎，，‎ ‎．‎ 直线所对应的函数关系式是，‎ 设 7分 易证得，，‎ ‎ 8分 整理得：‎ ‎，， 9分 由此，，‎ y x A B D M O P E ‎ 10分 当时，点在边上，‎ 此时，，，‎ 易证：‎ ‎，‎ ‎ 11分 ‎．‎ 综上所述： 12分 ‎（1）解法2：，．‎ 易求得： 2分 ‎（3）解法2：分别过作，，垂足分别为和，‎ 由（1）得，，‎ 即：，又，‎ 设经过的直线所对应的函数关系式是 则 解得： 7分 经过的直线所对应的函数关系式是．‎ 依题意：当时，在边上，在直线上，‎ ‎ 8分 整理得：‎ ‎ 9分 ‎ （） 10分 当时，点在上，此时，点坐标是，因为在直线上，‎ 整理得：．．‎ ‎ 11分 综上所述： 12分