- 2021-05-13 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
烟台市2015年中考数学卷
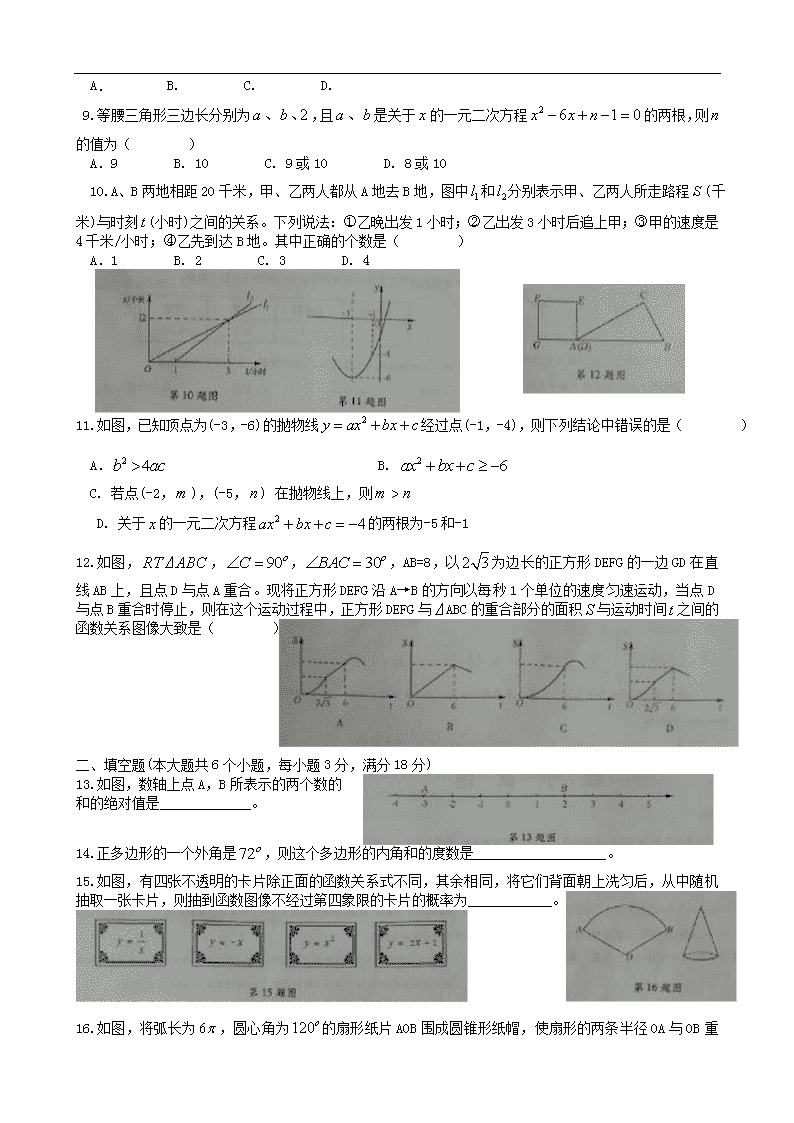
2015年烟台市初中学业水平考试 数学试题 一、选择题(本题共12各小题,每小题3分,满分36分) 1. 的相反数是( ) A. B. C. D. 2. 剪纸是我国最古老的民间艺术之一,被列入第四批《人类非物质文化遗产代表作名录》,下列剪纸作品中,是中心对称图形但不是轴对称图形的是( ) 3. 如图,讲一个圆柱体放置在长方体上,其中圆柱体的底面直径与长方体的宽相等,则该几何体的左视图是( ) 4. 下列式子不一定成立的是( ) A. B. C. D. 5. 李华根据演讲比赛中九位评委所给的分数制作了如下表格: 平均数 中位数 众数 方差 8.5 8.3 8.1 0.15 如果要去掉一个最高分和一个最低分,则表中数据一定不发生变化的是( ) A.平均数 B. 众数 C. 方差 D.中位数 6. 如果,那么的值为( ) A.2或-1 B. 0或1 C. 2 D. -1 7. 如图,BD是菱形ABCD的对角线,CE⊥AB于点E,且点E是AB的中点,则的值是 A. B. 2 C. D. 8.如图,正方形ABCD的边长为2,其面积标记为,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外做正方形,其面积标记为,…,按照此规律继续下去,则的值为( ) A. B. C. D. 9.等腰三角形三边长分别为,且是关于的一元二次方程的两根,则的值为( ) A.9 B. 10 C. 9或10 D. 8或10 10.A、B两地相距20千米,甲、乙两人都从A地去B地,图中和分别表示甲、乙两人所走路程(千米)与时刻(小时)之间的关系。下列说法:乙晚出发1小时;乙出发3小时后追上甲;甲的速度是4千米/小时;乙先到达B地。其中正确的个数是( ) A.1 B. 2 C. 3 D. 4 11.如图,已知顶点为(-3,-6)的抛物线经过点(-1,-4),则下列结论中错误的是( ) A. B. C. 若点(-2,),(-5,) 在抛物线上,则 D. 关于的一元二次方程的两根为-5和-1 12.如图,,,,AB=8,以为边长的正方形DEFG的一边GD在直线AB上,且点D与点A重合。现将正方形DEFG沿A→B的方向以每秒1个单位的速度匀速运动,当点D与点B重合时停止,则在这个运动过程中,正方形DEFG与⊿ABC的重合部分的面积与运动时间之间的函数关系图像大致是( ) 二、填空题(本大题共6个小题,每小题3分,满分18分) 13.如图,数轴上点A,B所表示的两个数的 和的绝对值是_____________。 14.正多边形的一个外角是,则这个多边形的内角和的度数是___________________。 15.如图,有四张不透明的卡片除正面的函数关系式不同,其余相同,将它们背面朝上洗匀后,从中随机抽取一张卡片,则抽到函数图像不经过第四象限的卡片的概率为 ____________。 16.如图,将弧长为,圆心角为 的扇形纸片AOB围成圆锥形纸帽,使扇形的两条半径OA与OB重合(接缝粘结部分忽略不计),则圆锥形纸帽的高是____________。 17.如图,矩形OABC的顶点A,C的 坐标分别是(4,0)(0,2),反比例 函数的图像过对角线 的交点P并且与AB,BC分别交 于D,E两点,连接OD,OE,DE, 则⊿ODE的面积为_____________。 18. 如图,直线与坐标轴交于AB两点,点是轴上一动点,一点M为圆心,2个单位长度为半径作⊙M,当⊙M与直线想切时,的值为__________________。 三、解答题(本大题共7个小题,满分66分) 19.(本题满分6分) 先化简,再从的范围内选取一个你喜欢的值代入求值。 20.(本题满分8分) “切实减轻学生课业负担”是我市作业改革的一项重要举措。某中学为了解本校学生平均每天的课外作业时间,随机抽取部分学生进行问卷调查,并将调查结果分为A、B、C、D四个等级。A:1小时以内,B:1小时-1.5小时,C:1.5小时-2小时,D:小时以上。根据调查结果绘制了如图所示的两幅不完整的统计图。请根据图中信息解答下列问题: (1)该校共调查了_________名学生; (2)请将条形统计图补充完整; (3)表示等级A的扇形圆心角的度 数是____________; (4)在此次问卷调查中,甲、乙两班 各有2人平均每天课外作业时间都 是2小时以上,从这4人中任选2人 去参加座谈,用列表或树状图的方法 求选出的2人来自不同班级的概率。 21.(本题满分8分) 2014年12月28日“青烟威荣”城际铁路正式开通,从烟台到北京的高铁里程比普快里程缩短了81千米,运行时间减少了9小时,已知烟台到北京的普快列车里程月1026千米,高铁平均时速是普快平均时速的2.5倍。 (1)求高铁列车的平均时速; (2)某日王老师要去距离烟台大约630千米的某市参加14:00召开的会议,如果他买到 当日8:40从烟台到该是的高铁票,而且从该市火车站到会议地点最多需要1.5小时。试问在高铁列车准点到达的情况下他能在开会之前赶到吗? 22.(本题满分9分) 如图1,滨海广场装有可利用风能、太阳能发电的风光互补环保路灯,灯杆顶端装有风力发电机,中间装有太阳能板,下端装有路灯。该系统工作过程中某一时刻的截面图如图2,已知太阳能板的支架BC垂直于灯杆OF,路灯顶端E距离地面6米,DE=1.8米,,且根据我市的地理位置设定太阳能板AB的倾斜角为,AB=1.5米,CD=1米。为保证长为1米的风力发电机叶片无障碍旋转,叶片与太阳能板顶端A的最近距离不得少于0.5米,求灯杆OF至少要多高?(利用科学计算器可求得,,,结果保留两位小数) 23.(本题满分9分) 如图,以⊿ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D,E,且。 (1)试判断⊿ABC的形状,并说明理由; (2)已知半圆的半径为5,BC=12,求的值。 24.(本题满分12分) 如图,在平面直角坐标系中,抛物线与⊙M相交于A、B、C、D四点。其中AB两点的坐标分别为(-1,0),(0,-2),点D在轴上且AD为⊙M的直径。点E是⊙M与轴的另一个交点,过劣弧上的点F作FH⊥AD于点H,且FH=1.5。 (1)求点D的坐标及该抛物线的表达式; (2)若点P是轴上的一个动点,试求出⊿PEF的周长最小时点P的坐标; (3)在抛物线的对称轴上是否存在点Q,使⊿QCM是等腰三角形?如果存在,请直接写出点Q的坐标;如果不存在,请说明理由。 25.(本题满分14分) 【问题提出】 如图,已知⊿ABC是等边三角形,点E在线段AB上,点D在直线BC上,且DE=EC,将⊿BCE绕点C顺时针旋转至⊿ACF,连接EF。 试证明:AB=DB+AF。 【类比探究】 (1)如图,如果点E在线段AB的延长线上,其它条件不变,线段AB、DB、AF之间又有怎样的数量关系?请说明理由。 (2)如果点E在线段BA的延长线上,其他条件不变,请在图的基础上将图形补充完整,并写出AB,DB,AF之间数量关系,不必说明理由。 参考答案 1. B 2. D 3. A 4. A 5. D 6. 7. D 8 9. B 10. C 11. C 12. A 13. 1。 14. 。 15. 。 16. 。 17. 。 18. 。 19. 解: 20.从条形图中我们可以看得出A的人数为60,B的人数为80,D的人数为20;从扇形统计图中我们能看到B占的比例40%,这样我们很容易就能得出共调查了200人,进而就能得出C的人数40人(图形可以自行补充)。A占的比重即扇形圆心角的度数为:。甲乙两班的学生我们分别标示为甲A、甲B、乙A、乙B,则一共有甲A和甲B、甲A和乙A、甲A和乙B、甲B和乙A、甲B和乙B、乙A和乙B。这样我们就很容易得出两人来自不同班级的概率为: 21. 路程 速度 时间 高铁 1026-81 普快 1026 根据上表,我们可以轻易得出方程: 解得: 所以即高铁的平均速度是180千米/小时。 第(2)问:从烟台到某市630千米 ,按照我们求出的高铁的速度,他需要3.5个小时到达A地,再加上1.5个小时,也就是说他至少需要5个小时到达会场。因此他购买8:40的票,则在13:40就能到达会场,所以在开会前是能够赶到的。 22. AB是直径,则我们很容易知道,同时也是。进而就有,而又,则DE=BE,进而,所以,而ABED可以看成是个圆内接四边形,则,所以,即⊿ABC为等腰三角形。 第(2)问要求的是的正弦值,由图知,在中,AB=10,要求正弦值,就必须求得AD的值,在中,我们可以利用等腰三角形一腰上的高求出AD=2.8,这样我们就能求出。 24.第(1)问求抛物线的解析式,我们知道的条件就是AB两点的坐标,要想求得抛物线的解析式,必须再有一个点才行。根据题意,设点M的坐标为(,0),根据两点间的距离公式(半径相等)可以求得,则点D的坐标为(4,0),这样就可以根据交点式来求解抛物线的解析式: 第(2)问其实是我们初中阶段经常练习的一个轴对称问题。要在轴上的找到一点P,使得⊿PEF的周长最小,我们先来看E,F两点,这是两个定点,也就是说EF的长度是不变的,那实际上这个题目就是求PE+PF的最小值,这就变成了轴对称问题中最为经典的“放羊问题”,要解决这一问题首先我们看图中有没有E或F的对称点,根据题意,显然是有E点的对称点B的,那么连接BF与轴的交点就是我们要求的点P(2,0)。 第(3)问要在抛物线的对称轴上找点Q,使得⊿QCM是等腰三角形,首先点M本身就在抛物线对称轴上,其坐标为;点C是点B关于抛物线对称轴的对称点,所以点C的坐标为(3,-2);求Q点的坐标,根据题意可设Q点为()。⊿QCM是等腰三角形,则可能有三种情况,分别是QC=MC;QM=MC;QC=QM。根据这三种情况就能求得Q点的坐标可能是或 或 25.第一问是个明显的旋转问题,根据旋转的特点,我们能够得出CE=CF,,即是等边三角形; ;,进而:,再有 又由已知DE=CE,知,所以有,这样就能得出 则有AE=BD,所以AB=AE+BE=BD+AF。第(2)问,根据第一问的做法,我们应该像第(1)问那样去证明,全等的条件都是有AF=BE(旋转得出),DE=EF,这样关键就在于说明。要想说明这两个角相等,我们可以像第(1)问一样去证出,,这样我们就能得出AF∥CD,此时我们需要把BD和EF的交点标示为G点,这样就有,接下来我们可以想办法证明(条件有一个公用角和小角),这样就得出了,所以就有,也就得出了三角形全等,这样就有AE=BD,所以这时AB=AE-BE=BD-AF。第(3)问画图略过,理由可以参考第(2)问。查看更多