- 2021-05-13 发布 |
- 37.5 KB |
- 13页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考与特殊四边形有关的填空压轴题
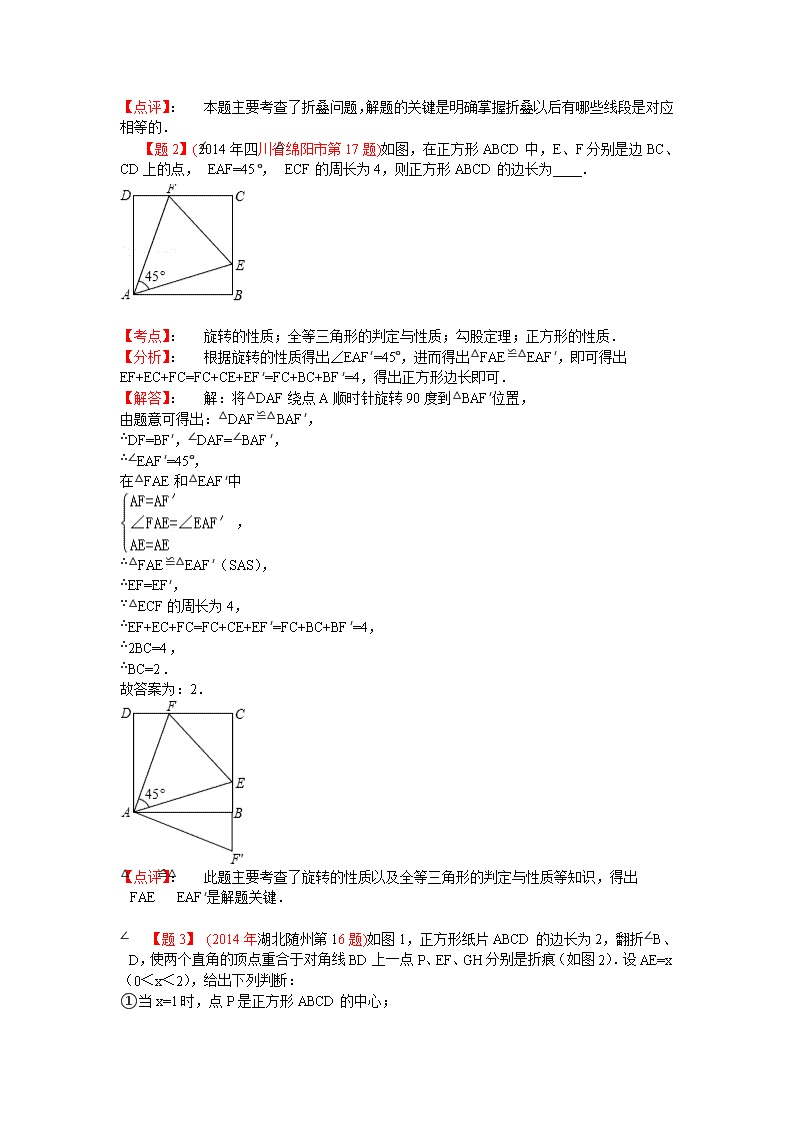
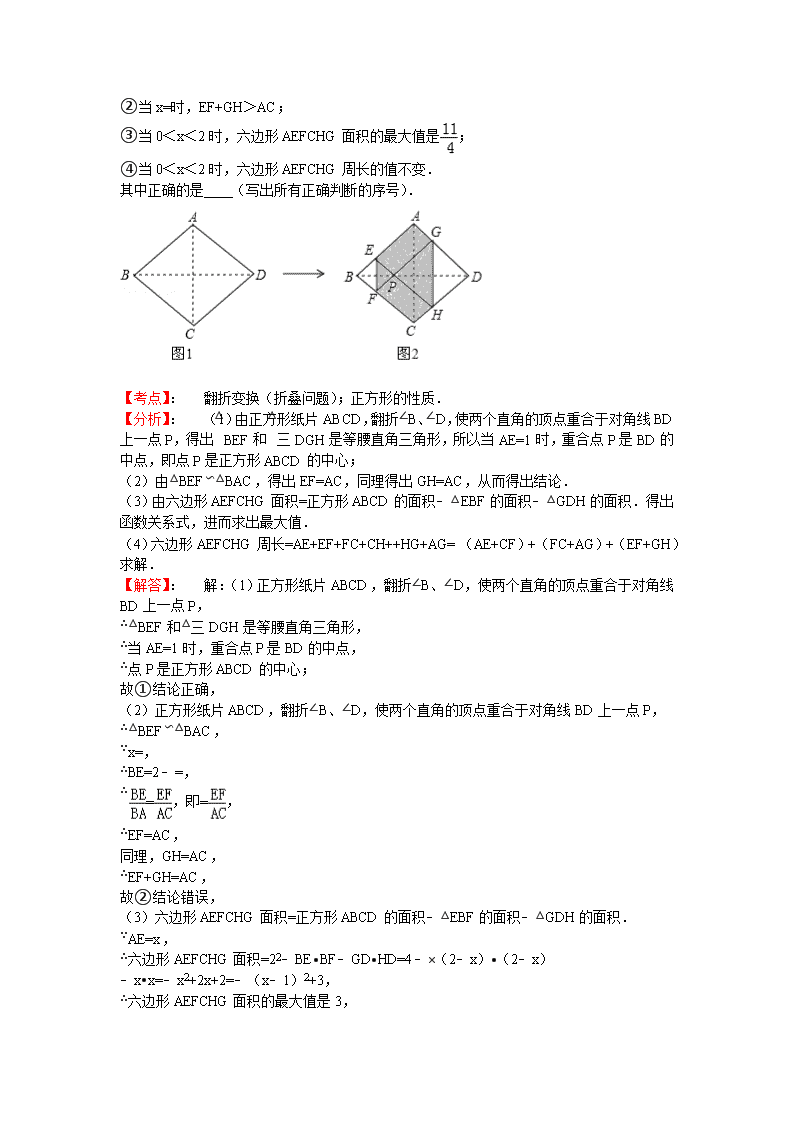
与特殊四边形有关的填空压轴题 2014年与特殊四边形(正多边形)有关的填空压轴题,题目展示涉及:折叠问题;旋转问题;三角形全等问题;平面展开﹣最短路径问题;动点问题的函数图象问题.知识点涉及:全等三角形的判定与性质;正方形的判定和性质;解直角三角形,勾股定理,正多边形性质;锐角三角函数.数学思想涉及:分类讨论;数形结合;方程思想. 现选取部分省市的2014年中考题展示. 【题1】(2014.年河南省第题)如图矩形ABCD中,AD=5,AB=7,点E为DC上一个动点,把△ADE沿AE折叠,当点D的对应点D′落在∠ABC的角平分线上时,DE的长为 . 【考点】: 翻折变换(折叠问题). 【分析】: 连接BD′,过D′作MN⊥AB,交AB于点M,CD于点N,作D′P⊥BC交BC于点P,先利用勾股定理求出MD′,再分两种情况利用勾股定理求出DE. 【解答】: 解:如图,连接BD′,过D′作MN⊥AB,交AB于点M,CD于点N,作D′P⊥BC交BC于点P, ∵点D的对应点D′落在∠ABC的角平分线上, ∴MD′=PD′, 设MD′=x,则PD′=BM=x, ∴AM=AB﹣BM=7﹣x, 又折叠图形可得AD=AD′=5, ∴x2+(7﹣x)2=25,解得x=3或4, 即MD′=3或4. 在RT△END′中,设ED′=a, ①当MD′=3时,D′E=5﹣3=2,EN=7﹣CN﹣DE=7﹣3﹣a=4﹣a, ∴a2=22+(4﹣a)2, 解得a=,即DE=, ②当MD′=4时,D′E=5﹣4=1,EN=7﹣CN﹣DE=7﹣4﹣a=3﹣a, ∴a2=12+(3﹣a)2, 解得a=,即DE=. 故答案为:或. 【点评】: 本题主要考查了折叠问题,解题的关键是明确掌握折叠以后有哪些线段是对应相等的. 【题2】(2014年四川省绵阳市第17题)如图,在正方形ABCD中,E、F分别是边BC、CD上的点,∠EAF=45°,△ECF的周长为4,则正方形ABCD的边长为 . 【考点】: 旋转的性质;全等三角形的判定与性质;勾股定理;正方形的性质. 【分析】: 根据旋转的性质得出∠EAF′=45°,进而得出△FAE≌△EAF′,即可得出EF+EC+FC=FC+CE+EF′=FC+BC+BF′=4,得出正方形边长即可. 【解答】: 解:将△DAF绕点A顺时针旋转90度到△BAF′位置, 由题意可得出:△DAF≌△BAF′, ∴DF=BF′,∠DAF=∠BAF′, ∴∠EAF′=45°, 在△FAE和△EAF′中 , ∴△FAE≌△EAF′(SAS), ∴EF=EF′, ∵△ECF的周长为4, ∴EF+EC+FC=FC+CE+EF′=FC+BC+BF′=4, ∴2BC=4, ∴BC=2. 故答案为:2. 【点评】: 此题主要考查了旋转的性质以及全等三角形的判定与性质等知识,得出△FAE≌△EAF′是解题关键. 【题3】 (2014年湖北随州第16题)如图1,正方形纸片ABCD的边长为2,翻折∠B、∠D,使两个直角的顶点重合于对角线BD上一点P、EF、GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断: ①当x=1时,点P是正方形ABCD的中心; ②当x=时,EF+GH>AC; ③当0<x<2时,六边形AEFCHG面积的最大值是; ④当0<x<2时,六边形AEFCHG周长的值不变. 其中正确的是 (写出所有正确判断的序号). 【考点】: 翻折变换(折叠问题);正方形的性质. 【分析】: (1)由正方形纸片ABCD,翻折∠B、∠D,使两个直角的顶点重合于对角线BD上一点P,得出△BEF和△三DGH是等腰直角三角形,所以当AE=1时,重合点P是BD的中点,即点P是正方形ABCD的中心; (2)由△BEF∽△BAC,得出EF=AC,同理得出GH=AC,从而得出结论. (3)由六边形AEFCHG面积=正方形ABCD的面积﹣△EBF的面积﹣△GDH的面积.得出函数关系式,进而求出最大值. (4)六边形AEFCHG周长=AE+EF+FC+CH++HG+AG=(AE+CF)+(FC+AG)+(EF+GH)求解. 【解答】: 解:(1)正方形纸片ABCD,翻折∠B、∠D,使两个直角的顶点重合于对角线BD上一点P, ∴△BEF和△三DGH是等腰直角三角形, ∴当AE=1时,重合点P是BD的中点, ∴点P是正方形ABCD的中心; 故①结论正确, (2)正方形纸片ABCD,翻折∠B、∠D,使两个直角的顶点重合于对角线BD上一点P, ∴△BEF∽△BAC, ∵x=, ∴BE=2﹣=, ∴=,即=, ∴EF=AC, 同理,GH=AC, ∴EF+GH=AC, 故②结论错误, (3)六边形AEFCHG面积=正方形ABCD的面积﹣△EBF的面积﹣△GDH的面积. ∵AE=x, ∴六边形AEFCHG面积=22﹣BE•BF﹣GD•HD=4﹣×(2﹣x)•(2﹣x)﹣x•x=﹣x2+2x+2=﹣(x﹣1)2+3, ∴六边形AEFCHG面积的最大值是3, 故③结论错误, (4)当0<x<2时, ∵EF+GH=AC, 六边形AEFCHG周长=AE+EF+FC+CH++HG+AG=(AE+CF)+(FC+AG)+(EF+GH)=2+2+2=4+2 故六边形AEFCHG周长的值不变, 故④结论正确. 故答案为:①④. 【点评】: 考查了翻折变换(折叠问题),菱形的性质,本题关键是得到EF+GH=AC,综合性较强,有一定的难度. 【题4】(2014江西第13题)如图,是将菱形ABCD以点O为中心按顺时针方向分别旋转90°,180°,270°后形成的图形。若,AB=2,则图中阴影部分的面积为______. 【考点】 菱形的性质,勾股定理,旋转的性质. 【分析】 连接AC、BD,AO、BO,AC与BD交于点E,求出菱形对角线AC长,根据旋转的性质可知AO⊥CO。在Rt△AOC中,根据勾股定理求出AO=CO=,从而求出Rt△AOC的面积,再减去△ACD的面积得阴影部分AOCD面积,一共有四个这样的面积,乘以4即得解。 【解答】 解:连接BD、AC,相交于点E,连接AO、CO。 ∵因为四边形ABCD是菱形, ∴AC ⊥BD,AB=AD=2。 ∵∠BAD=60°, ∴△ABD是等边三角形,BD=AB=2, ∴∠BAE=∠BAD=30°,AE=AC,BE=DE=BD=1, 在Rt△ABE中,AE=, ∴AC=2。 ∵菱形ABCD以点O为中心按顺时针方向旋转90°,180°,270°, ∴∠AOC=×360°=90°,即AO⊥CO,AO=CO 在Rt△AOC中,AO=CO=。 ∵S△AOC=AO·CO=××=3,S△ADC=AC·DE=×2×1=, ∴S阴影=S△AOC -S△ADC=4×(3-)=12-4 所以图中阴影部分的面积为12-4。 【题5】 (2014年河南省第14题)如图,在菱形ABCD中,AB=1,∠DAB=60°,把菱形ABCD绕点A顺时针旋转30°得到菱形AB′C′D′,其中点C的运动路径为,则图中阴影部分的面积为 . 【考点】: 菱形的性质;扇形面积的计算;旋转的性质. 【分析】: 连接BD′,过D′作D′H⊥AB,则阴影部分的面积可分为3部分,再根据菱形的性质,三角形的面积公式以及扇形的面积公式计算即可. 【解答】: 解:连接BD′,过D′作D′H⊥AB, ∵在菱形ABCD中,AB=1,∠DAB=60°,把菱形ABCD绕点A顺时针旋转30°得到菱形AB′C′D′, ∴D′H=, ∴S△ABD′=1×=, ∴图中阴影部分的面积为+﹣, 故答案为:+﹣. 【点评】: 本题考查了旋转的性质,菱形的性质,扇形的面积公式,熟练掌握旋转变换只改变图形的位置不改变图形的形状与大小是解题的关键. 【题6】(2014•泰州第16题)如图,正方向ABCD的边长为3cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q.若PQ=AE,则AP等于 cm. 【考点】: 全等三角形的判定与性质;正方形的性质;解直角三角形 【专题】: 分类讨论. 【分析】: 根据题意画出图形,过P作PN⊥BC,交BC于点N,由ABCD为正方形,得到AD=DC=PN,在直角三角形ADE中,利用锐角三角函数定义求出DE的长,进而利用勾股定理求出AE的长,根据M为AE中点求出AM的长,利用HL得到三角形ADE与三角形PQN全等,利用全等三角形对应边,对应角相等得到DE=NQ,∠DAE=∠NPQ=30°,再由PN与DC平行,得到∠PFA=∠DEA=60°,进而得到PM垂直于AE,在直角三角形APM中,根据AM的长,利用锐角三角函数定义求出AP的长,再利用对称性确定出AP′的长即可. 【解答】: 解:根据题意画出图形,过P作PN⊥BC,交BC于点N, ∵四边形ABCD为正方形, ∴AD=DC=PN, 在Rt△ADE中,∠DAE=30°,AD=3cm, ∴tan30°=,即DE=cm, 根据勾股定理得:AE==2cm, ∵M为AE的中点, ∴AM=AE=cm, 在Rt△ADE和Rt△PNQ中, , ∴Rt△ADE≌Rt△PNQ(HL), ∴DE=NQ,∠DAE=∠NPQ=30°, ∵PN∥DC, ∴∠PFA=∠DEA=60°, ∴∠PMF=90°,即PM⊥AF, 在Rt△AMP中,∠MAP=30°,cos30°=, ∴AP===2cm; 由对称性得到AP′=DP=AD﹣AP=3﹣2=1cm, 综上,AP等于1cm或2cm. 故答案为:1或2. 【点评】: 此题考查了全等三角形的判定与性质,正方形的性质,熟练掌握全等三角形的判定与性质是解本题的关键. 【题7】 (2014年重庆市第18题)如图,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,且DE=2CE,过点C作CF⊥BE,垂足为F,连接OF,则OF的长为 . 【考点】: 全等三角形的判定与性质;等腰直角三角形;正方形的性质. 【分析】: 在BE上截取BG=CF,连接OG,证明△OBG≌△OCF,则OG=OF,∠BOG=∠COF,得出等腰直角三角形GOF,在RT△BCE中,根据射影定理求得GF的长,即可求得OF的长. 【解答】: 解:如图,在BE上截取BG=CF,连接OG, ∵RT△BCE中,CF⊥BE, ∴∠EBC=∠ECF, ∵∠OBC=∠OCD=45°, ∴∠OBG=∠OCF, 在△OBG与△OCF中 ∴△OBG≌△OCF(SAS) ∴OG=OF,∠BOG=∠COF, ∴OG⊥OF, 在RT△BCE中,BC=DC=6,DE=2EC, ∴EC=2, ∴BE===2, ∵BC2=BF•BE, 则62=BF,解得:BF=, ∴EF=BE﹣BF=, ∵CF2=BF•EF, ∴CF=, ∴GF=BF﹣BG=BF﹣CF=, 在等腰直角△OGF中 OF2=GF2, ∴OF=. 【点评】: 本题考查了全等三角形的判定和性质,直角三角形的判定以及射影定理、勾股定理的应用. 【题8】 (2014年宁夏第15题)如图,在四边形ABCD中,AD∥BC,AB=CD=2,BC=5,∠BAD的平分线交BC于点E,且AE∥CD,则四边形ABCD的面积为 . 【考点】: 平行四边形的判定与性质;等边三角形的判定与性质. 【分析】: 根据题意可以判定△ABE是等边三角形,求得该三角形的高即为等腰梯形ABCD的高.所以利用梯形的面积公式进行解答. 【解答】: 解:如图,过点A作AF⊥BC于点F. ∵AD∥BC, ∴∠DAE=∠AEB, 又∵∠BAE=∠DAE, ∴∠BAE=∠AEB, ∵AE∥CD, ∴∠AEB=∠C, ∵AD∥BC,AB=CD=2, ∴四边形是等腰梯形, ∴∠B=∠C, ∴△ABE是等边三角形, ∴AB=AE=BE=2,∠B=60°, ∴AF=AB•sin60°=2×=, ∵AD∥BC,AE∥CD, ∴四边形AECD是平行四边形, ∴AD=EC=BC﹣BE=5﹣2=3, ∴梯形的面积=(AD+BC)×AF=×(3+5)×=4. 【点评】: 本题考查了等边三角形的判定和性质,平行四边形的判定和性质,等腰梯形的性质等. 【题9】(2014•宁波第11题)如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是 . 【考点】: 直角三角形斜边上的中线;勾股定理;勾股定理的逆定理. 【分析】: 连接AC、CF,根据正方形性质求出AC、CF,∠ACD=∠GCF=45°,再求出∠ACF=90°,然后利用勾股定理列式求出AF,再根据直角三角形斜边上的中线等于斜边的一半解答即可. 【解答】: 解:如图,连接AC、CF, ∵正方形ABCD和正方形CEFG中,BC=1,CE=3, ∴AC=,CF=3, ∠ACD=∠GCF=45°, ∴∠ACF=90°, 由勾股定理得,AF===2, ∵H是AF的中点, ∴CH=AF=×2=. 【点评】: 本题考查了直角三角形斜边上的中线等于斜边的一半的性质,正方形的性质,勾股定理,熟记各性质并作辅助线构造出直角三角形是解题的关键. 【题10】(2014•武汉第16题)如图,在四边形ABCD中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,则BD的长为__________. 【考点】: 全等三角形的判定与性质;勾股定理;等腰直角三角形 【分析】: 根据等式的性质,可得∠BAD与∠CAD′的关系,根据SAS,可得△BAD与△CAD′的关系,根据全等三角形的性质,可得BD与CD′的关系,根据勾股定理,可得答案. 【解答】: 解:作AD′⊥AD,AD′=AD,连接CD′,DD′,如图:, ∵∠BAC+∠CAD=∠DAD′+∠CAD, 即∠BAD=∠CAD′, 在△BAD与△CAD′中, , ∴△BAD≌△CAD′(SAS), ∴BD=CD′. ∠DAD′=90° 由勾股定理得DD′=, ∠D′DA+∠ADC=90° 由勾股定理得CD′=, ∴BD=CD′=, 故答案为:. 【点评】: 本题考查了全等三角形的判定与性质,利用了全等三角形的判定与性质,勾股定理,作出全等图形是解题关键. 【题11】(2014•苏州第17题)如图,在矩形ABCD中,=,以点B为圆心,BC长为半径画弧,交边AD于点E.若AE•ED=,则矩形ABCD的面积为 . 【考点】: 矩形的性质;勾股定理. 【分析】: 连接BE,设AB=3x,BC=5x,根据勾股定理求出AE=4x,DE=x,求出x的值,求出AB、BC,即可求出答案. 【解答】: 解:如图,连接BE,则BE=BC. 设AB=3x,BC=5x, ∵四边形ABCD是矩形, ∴AB=CD=3x,AD=BC=5x,∠A=90°, 由勾股定理得:AE=4x, 则DE=5x﹣4x=x, ∵AE•ED=, ∴4x•x=, 解得:x=(负数舍去), 则AB=3x=,BC=5x=, ∴矩形ABCD的面积是AB×BC=×=5, 故答案为:5. 【点评】: 本题考查了矩形的性质,勾股定理的应用,解此题的关键是求出x的值,题目比较好,难度适中. 【题129】(2014•枣庄第18题)图①所示的正方体木块棱长为6cm,沿其相邻三个面的对角线(图中虚线)剪掉一角,得到如图②的几何体,一只蚂蚁沿着图②的几何体表面从顶点A爬行到顶点B的最短距离为____________cm. 【考点】: 平面展开-最短路径问题;截一个几何体 【分析】: 要求蚂蚁爬行的最短距离,需将图②的几何体表面展开,进而根据“两点之间线段最短”得出结果. 【解答】: 解:如图所示: △BCD是等腰直角三角形,△ACD是等边三角形, 在Rt△BCD中,CD==6cm, ∴BE=CD=3cm, 在Rt△ACE中,AE==3cm, ∴从顶点A爬行到顶点B的最短距离为(3+3)cm. 故答案为:(3+3). 【点评】: 考查了平面展开﹣最短路径问题,本题就是把图②的几何体表面展开成平面图形,根据等腰直角三角形的性质和等边三角形的性质解决问题. 【题13】 (2014年江苏徐州第18题)如图①,在正方形ABCD中,点P沿边DA从点D开始向点A以1cm/s的速度移动;同时,点Q沿边AB、BC从点A开始向点C以2cm/s的速度移动.当点P移动到点A时,P、Q同时停止移动.设点P出发xs时,△PAQ的面积为ycm2,y与x的函数图象如图②,则线段EF所在的直线对应的函数关系式为 . 【考点】:动点问题的函数图象. 【分析】:根据从图②可以看出当Q点到B点时的面积为9,求出正方形的边长,再利用三角形的面积公式得出EF所在的直线对应的函数关系式. 【解答】:解:∵点P沿边DA从点D开始向点A以1cm/s的速度移动;点Q沿边AB、BC从点A开始向点C以2cm/s的速度移动. ∴当P点到AD的中点时,Q到B点, 从图②可以看出当Q点到B点时的面积为9, ∴9=×(AD)•AB, ∵AD=AB, ∴AD=6,即正方形的边长为6, 当Q点在BC上时,AP=6﹣x,△APQ的高为AB, ∴y=(6﹣x)×6,即y=﹣3x+18. 故答案为:y=﹣3x+18. 【点评】:本题主要考查了动点函数的图象,解决本题的关键是求出正方形的边长.查看更多