2020年中考数学压轴题：动点综合问题考点专练

2020年中考数学压轴题：动点综合问题考点专练

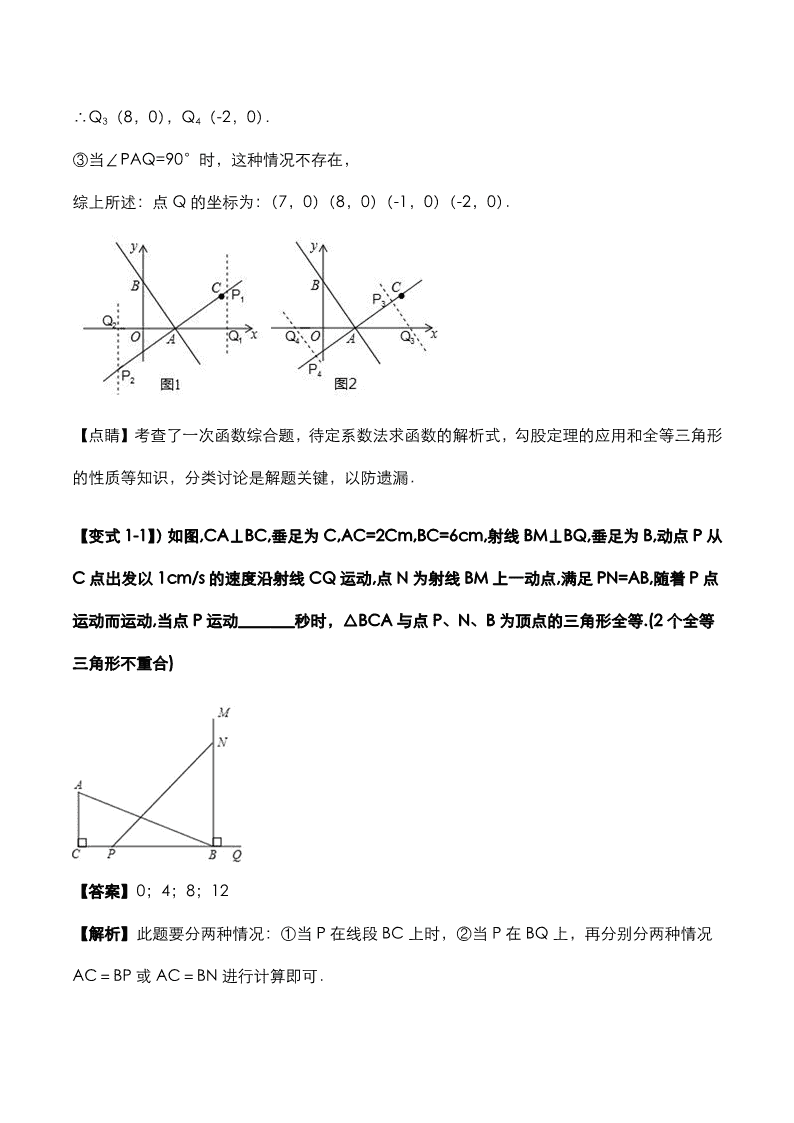
2020 年中考数学压轴题：动点综合问题考点专练 【典例分析】 【考点 1】动点之全等三角形问题 【例 1】如图，直线 4 43y x   与 x 轴和 y 轴分别交于 ,A B 两点，另一条直线过点 A和点 (7,3)C . (1)求直线 AC 的函数表达式; (2)求证: AB AC ; (3)若点 P 是直线 AC 上的一个动点，点Q是 x 轴上的一个动点，且以 , ,P Q A为顶点的三角形 与 AOB 全等，求点Q的坐标. 【答案】(1) 3 9 4 4y x  ;(2) 2 2 2AB AD BD  ; (3) 点Q的坐标为(7,0) 或(8,0) 或( 1,0) 或 ( 2,0) 【解析】（1）在 y=- 4 3 x+4 中，令 y=0，则 0=- 4 3 x+4，求得 A（3，0），设直线 AC 对应的函 数关系式为 y=kx+b，解方程组即可得到结论； （2）在直线 ABy=- 4 3 x+4 中，得到 k1=- 4 3 ，在直线 ACy＝ 3 4 x− 9 4 中，得到 k2= 3 4 ，由于 k1•k2=-1， 即可得到结论； （3）根据勾股定理得到 AB=5，①当∠AQP=90°时，如图 1，由全等三角形的性质得到 AQ=OB=4，于是得到 Q1（7，0），Q2（-1，0），②当∠APQ=90°时，如图 2，根据全等三 角形的性质得到 AQ=AB=5，于是得到 Q3（8，0），Q4（-2，0），③当∠PAQ=90°时，这种 情况不存在． 【详解】（1）在 y=- 4 3 x+4 中， 令 y=0，则 0=- 4 3 x+4， ∴x=3， ∴A（3，0）， 设直线 AC 对应的函数关系式为 y=kx+b， 则： 0 3 3 7 k b k b    ＝ ＝ ，解得： 3 4 9 4 k b     ＝ ＝ ， ∴直线 AC 对应的函数关系式为 y＝ 3 4 x- 9 4 . (2) 在直线 ABy=- 4 3 x+4 中， ∵k1=- 4 3 ， 在直线 ACy＝ 3 4 x− 9 4 中，k2= 3 4 ， ∴k1•k2=-1， ∴AB⊥AC；（3）在 y=- 4 3 x+4 中， 令 x=0，则 y=4， ∴OA=3，OB=4，由勾股定理得 AB=5， ①当∠AQP=90°时，如图 1，∵△AOB≌△AQP， ∴AQ=OB=4， ∴Q1（7，0），Q2（-1，0）， ②当∠APQ=90°时，如图 2，∵△AOB≌△AQP， ∴AQ=AB=5， ∴Q3（8，0），Q4（-2，0）． ③当∠PAQ=90°时，这种情况不存在， 综上所述：点 Q 的坐标为：（7，0）（8，0）（-1，0）（-2，0）． 【点睛】考查了一次函数综合题，待定系数法求函数的解析式，勾股定理的应用和全等三角形 的性质等知识，分类讨论是解题关键，以防遗漏． 【变式 1-1】）如图,CA⊥BC,垂足为 C,AC=2Cm,BC=6cm,射线 BM⊥BQ,垂足为 B,动点 P 从 C 点出发以 1cm/s 的速度沿射线 CQ 运动,点 N 为射线 BM 上一动点,满足 PN=AB,随着 P 点 运动而运动,当点 P 运动_______秒时，△BCA 与点 P、N、B 为顶点的三角形全等.(2 个全等 三角形不重合) 【答案】0；4；8；12 【解析】此题要分两种情况：①当 P 在线段 BC 上时，②当 P 在 BQ 上，再分别分两种情况 AC＝BP 或 AC＝BN 进行计算即可． 【详解】解：①当 P 在线段 BC 上，AC＝BP 时，△ACB≌△PBN， ∵AC＝2， ∴BP＝2， ∴CP＝6−2＝4， ∴点 P 的运动时间为 4÷1＝4（秒）； ②当 P 在线段 BC 上，AC＝BN 时，△ACB≌△NBP， 这时 BC＝PN＝6，CP＝0，因此时间为 0 秒； ③当 P 在 BQ 上，AC＝BP 时，△ACB≌△PBN， ∵AC＝2， ∴BP＝2， ∴CP＝2＋6＝8， ∴点 P 的运动时间为 8÷1＝8（秒）； ④当 P 在 BQ 上，AC＝NB 时，△ACB≌△NBP， ∵BC＝6， ∴BP＝6， ∴CP＝6＋6＝12， 点 P 的运动时间为 12÷1＝12（秒）， 故答案为：0 或 4 或 8 或 12． 【点睛】本题考查三角形全等的判定方法，判定两个三角形全等时必须有边的参与，若有两边 一角对应相等时，角必须是两边的夹角． 【考点 2】动点之直角三角形问题 【例 2】（模型建立） （1）如图 1，等腰直角三角形 ABC 中， 90ACB   ，CB CA ，直线 ED 经过点C ，过 A作 AD ED 于点 D ，过 B 作 BE ED 于点 E .求证： BEC CDA   ； （模型应用） （2）已知直线 1l ： 4 43y x  与坐标轴交于点 A、B ，将直线 1l 绕点 A逆时针旋转 45 至直线 2l ， 如图 2，求直线 2l 的函数表达式； （3）如图 3，长方形 ABCO，O为坐标原点，点 B 的坐标为 8, 6 ，点 A、C 分别在坐标轴 上，点 P 是线段 BC 上的动点，点 D 是直线 2 6y x   上的动点且在第四象限.若 APD 是以点 D 为直角顶点的等腰直角三角形，请直接．．写出点 D 的坐标. 【答案】（1）见解析；（2）y＝−7x−21；（3）D（4，−2）或（ 20 3 ， 22 3  ）. 【解析】（1）根据△ABC 为等腰直角三角形，AD⊥ED，BE⊥ED，可判定 BEC CDA   ； （2）①过点 B 作 BC⊥AB，交 l2 于 C，过 C 作 CD⊥y 轴于 D，根据△CBD≌△BAO，得出 BD＝AO＝3，CD＝OB＝4，求得 C（−4，7），最后运用待定系数法求直线 l2 的函数表达式； （3）根据△APD 是以点 D 为直角顶点的等腰直角三角形，当点 D 是直线 y＝−2x＋6 上的动 点且在第四象限时，分两种情况：当点 D 在矩形 AOCB 的内部时，当点 D 在矩形 AOCB 的 外部时，设 D（x，−2x＋6），分别根据△ADE≌△DPF，得出 AE＝DF，据此列出方程进行求 解即可． 【详解】解：（1）证明：∵△ABC 为等腰直角三角形， ∴CB＝CA，∠ACD＋∠BCE＝90°， 又∵AD⊥ED，BE⊥ED， ∴∠D＝∠E＝90°，∠EBC＋∠BCE＝90°， ∴∠ACD＝∠EBC， 在△ACD 与△CBE 中， D E ACD EBC CA CB      ＝ ＝ ＝ ， ∴ BEC CDA   （AAS）； （2）①如图 2，过点 B 作 BC⊥AB，交 l2 于 C，过 C 作 CD⊥y 轴于 D， ∵∠BAC＝45°， ∴△ABC 为等腰直角三角形， 由（1）可知：△CBD≌△BAO， ∴BD＝AO，CD＝OB， ∵直线 l1：y＝ 4 3 x＋4 中，若 y＝0，则 x＝−3；若 x＝0，则 y＝4， ∴A（−3，0），B（0，4）， ∴BD＝AO＝3，CD＝OB＝4， ∴OD＝4＋3＝7， ∴C（−4，7）， 设 l2 的解析式为 y＝kx＋b，则 7 4 0 3 k b k b        ， 解得： 7 21 k b      ， ∴l2 的解析式为：y＝−7x−21； （3）D（4，−2）或（ 20 3 ， 22 3  ）． 理由：当点 D 是直线 y＝−2x＋6 上的动点且在第四象限时，分两种情况： 当点 D 在矩形 AOCB 的内部时，如图，过 D 作 x 轴的平行线 EF，交直线 OA 于 E，交 BC 于 F， 设 D（x，−2x＋6），则 OE＝2x−6，AE＝6−（2x−6）＝12−2x，DF＝EF−DE＝8−x， 由（1）可得，△ADE≌△DPF，则 DF＝AE，即：12−2x＝8−x， 解得 x＝4， ∴−2x＋6＝−2， ∴D（4，−2）， 此时，PF＝ED＝4，CP＝6＝CB，符合题意； 当点 D 在矩形 AOCB 的外部时，如图，过 D 作 x 轴的平行线 EF，交直线 OA 于 E，交直线 BC 于 F， 设 D（x，−2x＋6），则 OE＝2x−6，AE＝OE−OA＝2x−6−6＝2x−12，DF＝EF−DE＝8−x， 同理可得：△ADE≌△DPF，则 AE＝DF，即：2x−12＝8−x， 解得 x＝ 20 3 ， ∴−2x＋6＝ 22 3  ， ∴D（ 20 3 ， 22 3  ）， 此时，ED＝PF＝ 20 3 ，AE＝BF＝ 4 3 ，BP＝PF−BF＝16 3 ＜6，符合题意， 综上所述，D 点坐标为：（4，−2）或（ 20 3 ， 22 3  ） 【点睛】本题属于一次函数综合题，主要考查了点的坐标、矩形的性质、待定系数法、等腰直 角三角形的性质以及全等三角形等相关知识的综合应用，解决问题的关键是作辅助线构造全等 三角形，运用全等三角形的性质进行计算，解题时注意分类思想的运用． 【变式 2-1】（2019·辽宁中考模拟）如图，已知二次函数 y＝ax2+bx+4 的图象与 x 轴交于点 A(4，0)和点 D(﹣1，0)，与 y 轴交于点 C，过点 C 作 BC 平行于 x 轴交抛物线于点 B，连接 AC (1)求这个二次函数的表达式； (2)点 M 从点 O 出发以每秒 2 个单位长度的速度向点 A 运动；点 N 从点 B 同时出发，以每秒 1 个单位长度的速度向点 C 运动，其中一个动点到达终点时，另一个动点也随之停动，过点 N 作 NQ 垂直于 BC 交 AC 于点 Q，连结 MQ. ①求△AQM 的面积 S 与运动时间 t 之间的函数关系式，写出自变量的取值范围；当 t 为何值 时，S 有最大值，并求出 S 的最大值； ②是否存在点 M，使得△AQM 为直角三角形？若存在，求出点 M 的坐标；若不存在，说明 理由． 【答案】(1)y＝﹣x2+3x+4；(2)①S=-t2+t+2；0≤t≤2；t＝ 1 2 时，S 最大值＝ 9 4 ；②存在，点 M 的坐标分别为(1，0)和(2，0)． 【解析】(1)由待定系数法将 AD 两点代入即可求解． (2)①分别用 t 表示出 AM、PQ，由三角形面积公式直接写出含有 t 的二次函数关系式，由二 次函数的最大值可得答案； ②分类讨论直角三角形的直角顶点，然后解出 t，求得 M 坐标． 【详解】(1)∵二次函数的图象经过 A(4，0)和点 D(﹣1，0)， ∴ 16 4 4 0 4 0 a b a b        ， 解得 1 3 a b     ， 所以，二次函数的解析式为 y＝﹣x2+3x+4． (2)①延长 NQ 交 x 轴于点 P， ∵BC 平行于 x 轴，C(0，4) ∴B(3，4)，NP⊥OA． 根据题意，经过 t 秒时，NB＝t，OM＝2t， 则 CN＝3﹣t，AM＝4﹣2t． ∵∠BCA＝∠MAQ＝45°， ∴QN＝CN＝3﹣t， ∴PQ＝NP﹣NQ＝4﹣(1﹣t)＝1+t， ∴S△AMQ= 1 2 AM×PQ= 1 2 (4-2t)(1+t) ＝﹣t2+t+2． ∴S=-t2+t+2=-(t- 1 2 )2+ 9 4 ． ∵a＝﹣1＜0，且 0≤t≤2，∴S 有最大值． 当 t＝ 1 2 时，S 最大值＝ 9 4 ． ②存在点 M，使得△AQM 为直角三角形． 设经过 t 秒时，NB＝t，OM＝2t， 则 CN＝3﹣t，AM＝4﹣2t， ∴∵∠BCA＝∠MAQ＝45°． Ⅰ．若∠AQM＝90°， 则 PQ 是等腰 Rt△MQA 底边 MA 上的高． ∴PQ 是底边 MA 的中线， ∴PQ＝AP＝ 1 2 MA， ∴1+t＝ 1 2 (4﹣2t)， 解得，t＝ 1 2 ， ∴M 的坐标为(1，0)． Ⅱ．若∠QMA＝90°，此时 QM 与 QP 重合． ∴QM＝QP＝MA， ∴1+t＝4﹣2t， ∴t＝1， ∴点 M 的坐标为(2，0)． 所以，使得△AQM 为直角三角形的点 M 的坐标分别为(1，0)和(2，0)． 【点睛】此题考查了待定系数法求解析式，还考查了三角形的面积，要注意利用点的坐标的意 义表示线段的长度，从而求出线段之间的关系还要注意求最大值可以借助于二次函数． 【变式 2-2】如图，四边形 ABCD 是正方形，以 DC 为边向外作等边△DCE，连接 AE 交 BD 于点 F，交 CD 于点 G，点 P 是线段 AE 上一动点，连接 DP、BP． （1）求∠AFB 的度数； （2）在点 P 从 A 到 E 的运动过程中，若 DP 平分∠CDE，求证：AG•DP＝DG•BD； （3）已知 AD＝6，在点 P 从 A 到 E 的运动过程中，若△DBP 是直角三角形，请求 DP 的长． 【答案】(1) 60°；(2)见解析；(3) DP=6 或 DP＝3 3 －3 或 DP＝3 6 3 2 时，△DBP 是 直角三角形 【解析】（1）根据正方形的性质、等边三角形的性质解答； （2）连接 AC，证明△DGP∽△AGC，根据相似三角形的对应边的比相等证明； （3）根据正方形的性质、勾股定理分别求出 BD、OD，根据直角三角形的性质求出 DF，分 ∠BPD＝90°、∠BDP＝90°两种情况，根据相似三角形的性质计算． 【详解】（1）∵四边形 ABCD 是正方形， ∴AB＝DC，∠ADC＝90°， 又∵△DCE 是等边三角形， ∴DE＝DC，∠EDC＝60°， ∴DA＝DE，∠ADE＝150°， ∴∠DAE＝15°， 又∠ADB＝45°， ∴∠AFB＝∠DAF+∠ADF＝15°+45°＝60°； （2）连接 AC， ∠CAG＝∠CAD﹣∠DAG＝45°﹣15°＝30°， ∵DP 平分∠CDE， ∴ 1 302GDP EDC     ， ∴∠PDG＝∠CAG， 又∠DGP＝∠AGC， ∴△DGP∽△AGC， ∴ DG DP AG AC  ，即 AG•DP＝DG•AC， ∵AC＝DB， ∴AG•DP＝DG•BD； （3）连接 AC 交 BD 于点 O，则∠AOF＝90°， ∵AD＝6， ∴0A 0D 3 2  ， 在 Rt△AOF 中，∠OAF＝30°， ∴ 6, 2 6OF AF  ， ∴ FD 3 2 6  ， 由图可知：0°＜∠DBP≤45°， 则△DBP 是直角三角形只有∠BPD＝90°和∠BDP＝90°两种情形： ①当∠BPD＝90°时， I、若点 P 与点 A 重合，∠BPD＝90°， ∴DP＝DA＝6； II、当点 P 在线段 AE 上时，∠BPD＝90°， 连接 OP， 1 3 22OP OA BD   ， ∴∠OPA＝∠OAP＝30°， ∴∠AOP＝120°， ∴∠FOP＝∠AOP﹣∠AOF＝30°， ∴∠DBP＝∠OPB＝15°， ∴∠FDP＝75°， 又∠BAF＝∠BAD﹣∠DAF＝75°， ∴∠BAF＝∠PDF， 又∠AFB＝∠DFP， ∴△BAF∽△PDF， ∴ DP DF AB AF  ，即 3 2 6 6 2 6 DP  解得， 3 3 3DP   ； ②当∠BDP＝90°时，∠DFP＝∠AFB＝60°， ∴DP＝DF×tan∠DFP＝ 3(3 2 6) 3 6 3 2   ， 综上，DP=6 或 DP＝3 3 －3 或 DP＝3 6 3 2 时，△DBP 是直角三角形． 【点睛】本题考查的是正方形的性质、相似三角形的判定和性质以及等边三角形的性质、直角 三角形的性质，掌握正方形的性质、相似三角形的判定定理和性质定理是解题的关键． 【考点 3】动点之等腰三角形问题 【例 3】（2019·湖南中考真题）如图一，在射线 DE 的一侧以 AD 为一条边作矩形 ABCD， 5 3AD  ， 5CD  ，点 M 是线段 AC 上一动点（不与点 A重合），连结 BM ，过点 M 作 BM 的 垂线交射线 DE 于点 N ，连接 BN ． （1）求 CAD 的大小； （2）问题探究：动点 M 在运动的过程中， ①是否能使 AMN 为等腰三角形，如果能，求出线段 MC 的长度；如果不能，请说明理由． ② MBN 的大小是否改变？若不改变，请求出 MBN 的大小；若改变，请说明理由． （3）问题解决： 如图二，当动点 M 运动到 AC 的中点时，AM与 BN 的交点为 F ，MN 的中点为 H ，求线段 FH 的长度． 【答案】（1） 30 CAD ；（2）①能，CM 的值为 5 或5 3 ；②大小不变， 30 MBN ；（3） 5 3 6 FH . 【解析】（1）在 Rt ADC 中，求出 DAC 的正切值即可解决问题． （2）①分两种情形：当 NA NM 时，当 AN AM 时，分别求解即可． ② 30MBN   ．利用四点共圆解决问题即可． （3）首先证明 ABM 是等边三角形，再证明 BN 垂直平分线段 AM ，解直角三角形即可解决问 题． 【详解】解：（1）如图一（1）中， ∵四边形 ABCD是矩形， ∴ 90ADC   ， ∵ DC 5 3tan AD 35 3    CAD ， ∴ 30 CAD ． （2）①如图一（1）中，当 AN NM 时， ∵ 90BAN BMN     ， BN BN ， AN NM ， ∴ Rt Rt ( )BNA BNM HL    ， ∴ BA BM ， 在 Rt ABC 中，∵ 30ACB DAC     ， 5AB CD  ， ∴ 2 10AC AB  ， ∵ 60BAM   ， BA BM ， ∴ ABM 是等边三角形， ∴ 5AM AB  ， ∴ 5CM AC AM   ． 如图一（2）中，当 AN AM 时，易证 15AMN ANM     ， ∵ 90BMN   ， ∴ 75CMB   ，∵ 30MCB   ， ∴ 180 75 30 75CBM         ， ∴ CMB CBM   ， ∴ 5 5CM CB  ， 综上所述，满足条件的CM 的值为 5 或5 3 ． ②结论： 30 MBN 大小不变． 理由：如图一（1）中，∵ 180BAN BMN     ， ∴ , , ,A B M N 四点共圆， ∴ 30MBN MAN     ． 如图一（2）中，∵ 90BMN BAN     ， ∴ , , ,A N B M 四点共圆， ∴ 180MBN MAN     ， ∵ 180DAC MAN     ， ∴ 30MBN DAC     ， 综上所述， 30 MBN ． （3）如图二中， ∵ AM MC ， ∴ BM AM CM  ， ∴ 2AC AB ， ∴ AB BM AM  ， ∴ ABM 是等边三角形， ∴ 60BAM BMA     ， ∵ 90BAN BMN     ， ∴ 30NAM NMA     ， ∴ NA NM ， ∵ BA BM ， ∴ BN 垂直平分线段 AM， ∴ 5 2FM  ， ∴ 5 3 cos30 3 FMNM   ， ∵ 90NFM   ， NH HM ， ∴ 1 5 3 2 6FH MN  ． 【点睛】本题属于四边形综合题，考查了矩形的性质，全等三角形的判定和性质，解直角三角 形，等边三角形的判定和性质，锐角三角函数，等腰三角形的判定和性质等知识，解题的关键 是灵活运用所学知识解决问题，学会用分类讨论的思想思考问题，属于中考压轴题． 【变式 3-1】如图①，已知正方形 ABCD边长为 2，点 P 是 AD 边上的一个动点，点 A关于直 线 BP 的对称点是点Q ，连结 PQ 、 DQ 、CQ 、 BQ .设 AP=x. （1）当 1x  时，求 BP 长； （2）如图②，若 PQ 的延长线交CD 边于 E ，并且 90CQD  o ，求证： CEQ 为等腰三角形； （3）若点 P 是射线 AD 上的一个动点，则当 CDQ 为等腰三角形时，求 x 的值. 【答案】（1）BP= 5 ；（2）证明见解析；（3）△CDQ 为等腰三角形时 x 的值为 4-2 3 、2 3 3 、 2 3 +4. 【解析】（1）利用勾股定理求出 BP 的长即可；（2）根据对称性质及正方形的性质可得 AB=BQ=BC，∠A=∠BQP=∠BCE=90°，可得∠BQE=90°，由第一视角相等性质可得 ∠BCQ=∠BQC，根据同角或等角的余角相等的性质可得∠EQC=∠ECQ，可得 EC=EQ，可 得结论；（3）若△CDQ 为等腰三角形，则边 CD 边为该等腰三角形的一腰或者底边．又 Q 点 为 A 点关于 PB 的对称点，则 AB=QB，以点 B 为圆心，以 AB 的长为半径画弧，则 Q 点只能 在弧 AB 上．若 CD 为腰，以点 C 为圆心，以 CD 的长为半径画弧，两弧交点即为使得△CDQ 为等腰三角形（CD 为腰）的 Q 点．若 CD 为底边，则作 CD 的垂直平分线，其与弧 AC 的 交点即为使得△CDQ 为等腰三角形（CD 为底）的 Q 点．则如图所示共有三个 Q 点，那么 也共有 3 个 P 点．作辅助线，利用直角三角形性质求之即可． 【详解】（1）∵AP=x=1，AB=2， ∴BP= 2 2AB AP = 5 ， （2）∵四边形 ABCD 是正方形， ∴AB=BC，∠A=∠BCD=90°． ∵Q 点为 A 点关于 BP 的对称点， ∴AB=QB，∠A=∠PQB=90°， ∴QB=BC，∠BQE=∠BCE=90°， ∴∠BQC=∠BCQ， ∴∠EQC+∠BQC=∠ECQ+∠BCQ=90°， ∴∠EQC =∠ECQ， ∴EQ=EC，即△CEQ 为等腰三角形. （3）如图，以点 B 为圆心，以 AB 的长为半径画弧，以点 C 为圆心，以 CD 的长为半径画弧， 两弧分别交于 Q1，Q3．此时△CDQ1，△CDQ3 都为以 CD 为腰的等腰三角形． 作 CD 的垂直平分线交弧 AC 于点 Q2，此时△CDQ2 以 CD 为底的等腰三角形． ①讨论 Q1，如图，连接 BQ1、CQ1，作 PQ1⊥BQ1 交 AD 于 P，过点 Q1，作 EF⊥AD 于 E， 交 BC 于 F， ∵△BCQ1 为等边三角形，正方形 ABCD 边长为 2， ∴FC=1，Q1F= 2 2 1CQ FC = 3 ，Q1E=2- 3 ， 在四边形 ABPQ1 中， ∵∠ABQ1=30°， ∴∠APQ1=150°， ∴∠EPQ1=30°，△PEQ1 为含 30°的直角三角形， ∴PE= 3 EQ1=2 3 -3， ∵EF 是 BC 的垂直平分线， ∴AE= 1 2 AD=1， ∴x=AP=AE-PE=1-(2 3 -3)=4-2 3 . ②讨论 Q2，如图，连接 BQ2，AQ2，过点 Q2 作 PG⊥BQ2，交 AD 于 P，交 CD 于 G，连接 BP，过点 Q2 作 EF⊥CD 于 E，交 AB 于 F， ∵EF 垂直平分 CD， ∴EF 垂直平分 AB， ∴AQ2=BQ2． ∵AB=BQ2， ∴△ABQ2 为等边三角形． ∴AF= 1 2 AE=1，FQ2= 2 2AE AF = 3 ， 在四边形 ABQ2P 中， ∵∠BAD=∠BQ2P=90°，∠ABQ2=60°， ∴∠APQ2=120°， ∴∠EQ2G=∠DPG=180°-120°=60°， ∴EQ2=EF-FQ2=2- 3 ， EG= 3 EQ2=2 3 -3， ∴DG=DE+GE=1+2 3 -3=2 3 -2， ∴DG= 3 PD，即 PD=2- 2 3 3 ， ∴x=AP=2-PD= 2 3 3 . ③对 Q3，如图作辅助线，连接 BQ1，CQ1，BQ3，CQ3，过点 Q3 作 PQ3⊥BQ3，交 AD 的延 长线于 P，连接 BP，过点 Q1，作 EF⊥AD 于 E，此时 Q3 在 EF 上，记 Q3 与 F 重合． ∵△BCQ1 为等边三角形，△BCQ3 为等边三角形，BC=2， ∴Q1Q2=2 3 ，Q1E=2- 3 ， ∴EF=2+ 3 ， 在四边形 ABQ3P 中 ∵∠ABF=∠ABC+∠CBQ3=150°， ∴∠EPF=30°， ∴EP= 3 EF=2 3 +3， ∵AE=1， ∴x=AP=AE+PE=1+2 3 +3=2 3 +4. 综上所述：△CDQ 为等腰三角形时 x 的值为 4-2 3 、 2 3 3 、2 3 +4. 【点睛】本题考查四边形的综合、正方形的性质、含 30°角的直角三角形的性质，第三问是 一个难度非常高的题目，可以利用尺规作图的思想将满足要求的点 Q 找全．另外求解各个 P 点也是勾股定理的综合应用熟练掌握并灵活运所学知识是解题关键． 【变式 3-2】（2019·河南中考模拟）如图，抛物线 y=ax2+bx+3 交 y 轴于点 A，交 x 轴于点 B（-3，0）和点 C（1，0），顶点为点 M． （1）求抛物线的解析式； （2）如图，点 E 为 x 轴上一动点，若△AME 的周长最小，请求出点 E 的坐标； （3）点 F 为直线 AB 上一个动点，点 P 为抛物线上一个动点，若△BFP 为等腰直角三角形， 请直接写出点 P 的坐标． 【答案】（1） 2 2 3y x x    ；（2）E（- 3 7 ，0）；（3）点 P 的坐标为（2，-5）或（1，0）． 【解析】（1）设抛物线的解析式为：y=a（x+3）（x-1），然后将点 A 的坐标代入函数解析式即 可求得此抛物线的解析式； （2）作 A 关于 x 轴的对称点 A′（0，-3），连接 MA′交 x 轴于 E，此时△AME 的周长最小， 求出直线 MA'解析式即可求得 E 的坐标； （3）如图 2，先求直线 AB 的解析式为：y=x+3，根据解析式表示点 F 的坐标为（m，m+3）， 分三种情况进行讨论： ①当∠PBF=90°时，由 F1P⊥x 轴，得 P（m，-m-3），把点 P 的坐标代入抛物线的解析式可 得结论； ②当∠BF3P=90°时，如图 3，点 P 与 C 重合， ③当∠BPF4=90°时，如图 3，点 P 与 C 重合， 从而得结论． 【详解】（1）当 x=0 时，y=3，即 A（0，3）， 设抛物线的解析式为：y=a（x+3）（x-1）， 把 A（0，3）代入得：3=-3a， a=-1， ∴y=-（x+3）（x-1）=-x2-2x+3， 即抛物线的解析式为：y=-x2-2x+3； （2）y=-x2-2x+3=-（x+1）2+4， ∴M（-1，4）， 如图 1，作点 A（0，3）关于 x 轴的对称点 A'（0，-3），连接 A'M 交 x 轴于点 E，则点 E 就 是使得△AME 的周长最小的点， 设直线 A′M 的解析式为：y=kx+b， 把 A'（0，-3）和 M（-1，4）代入得： 4 3 k b b ＝ ＝     ， 解得： 7 3 k b    ＝ ＝ ∴直线 A'M 的解析式为：y=-7x-3， 当 y=0 时，-7x-3=0， x=- 3 7 ， ∴点 E（- 3 7 ，0）， （3）如图 2，易得直线 AB 的解析式为：y=x+3， 设点 F 的坐标为（m，m+3）， ①当∠PBF=90°时，过点 B 作 BP⊥AB，交抛物线于点 P，此时以 BP 为直角边的等腰直角三 角形有两个，即△BPF1 和△BPF2， ∵OA=OB=3， ∴△AOB 和△A'OB 是等腰直角三角形， ∴∠F1BC=∠BF1P=45°， ∴F1P⊥x 轴， ∴P（m，-m-3）， 把点 P 的坐标代入抛物线的解析式 y=-x2-2x+3 中得： -m-3=-m2-2m+3， 解得：m1=2，m2=-3（舍）， ∴P（2，-5）； ②当∠BF3P=90°时，如图 3， ∵∠F3BP=45°，且∠F3BO=45°， ∴点 P 与 C 重合， 故 P（1，0）， ③当∠BPF4=90°时，如图 3， ∵∠F4BP=45°，且∠F4BO=45°， ∴点 P 与 C 重合， 故 P（1，0）， 综上所述，点 P 的坐标为（2，-5）或（1，0）． 【点睛】此题考查了待定系数法求函数的解析式，周长最短问题，等腰直角三角形的性质和判 定等知识．此题综合性很强，解题的关键是注意数形结合和分类讨论思想的应用． 【变式 3-3】（2019·广西中考真题）已知抛物线 2y mx 和直线 y x b   都经过点  2,4M  ， 点O为坐标原点，点 P 为抛物线上的动点，直线 y x b   与 x 轴、 y 轴分别交于 A B、 两点． （1）求 m b、 的值； （2）当 PAM 是以 AM 为底边的等腰三角形时，求点 P 的坐标； （3）满足（2）的条件时，求sin BOP 的值． 【答案】（1） 1m  ； 2b  ；（2）点 P 的坐标为  1,1 或 2,4 ；（3）sin BOP 的值为 2 2 或 5 5 ． 【解析】(1)根据点 M 的坐标，利用待定系数法可求出 ,m b的值； (2)由(1)可得出抛物线及直线 AB 的解析式，继而可求出点 A的坐标，设点 P 的坐标为 2( , )x x ， 结合点 ,A M 的坐标可得出 2 2,PA PM 的值，再利用等腰三角形的性质可得出关于 x 的方程，解 之即可得出结论； (3)过点 P 作 PN y 轴，垂足为点 N ，由点 P 的坐标可得出 ,PN PO 的长，再利用正弦的定义 即可求出sin BOP 的值． 【详解】(1)将  2,4M  代入 2y mx ，得：4 4m ， ∴ 1m  ； 将  2,4M  代入 y x b   ，得： 4 2 b  ， ∴ 2b  ； (2)由(1)得：抛物线的解析式为 2y x= ，直线 AB 的解析式为 2y x   ， 当 0y  时， 2 0x   ， 解得： 2x  ， ∴点 A的坐标为 2,0 ， 2OA  ， 设点 P 的坐标为 2( , )x x ，则  22 2 2 4 22 0 4( ) 4PA x x x x x        ，  22 2 2 4 2( )2 4 7 4 20PM x x x x x         ， ∵ PAM 是以 AM为底边的等腰三角形， ∴ 2 2PA PM ，即 4 2 4 24 4 7 4 20x x x x x x       ， 整理，得： 2 2 0x x   ， 解得： 1 21, 2x x   ， ∴点 P 的坐标为  1,1 或 2,4 ； (3)过点 P 作 PN y 轴，垂足为点 N ，如图所示， 当点 P 的坐标为  1,1 时， 1PN  ， 2 21 1 2PO    ， ∴ 2sin 2 PNBOP PO    ； 当点 P 的坐标为 2,4 时， 2PN  ， 2 22 4 2 5PO    ， ∴ 5sin 5 PNBOP PO    ， ∴满足(2)的条件时，sin BOP 的值的值为 2 2 或 5 5 ． 【点睛】本题考查了待定系数法求一次函数解析式、待定系数法求二次函数解析式、一次函数 图象上点的坐标特征、等腰三角形的性质、勾股定理以及解直角三角形，解题的关键是：(1) 根据点的坐标，利用待定系数法求出 ,m b的值；(2)利用勾股定理及等腰三角形的性质，找出 关于 x 的方程；(3)通过解直角三角形，求出sin BOP 的值． 【考点 4】动点之相似三角形问题 【例 4】在边长为4 的正方形 ABCD中，动点 E 以每秒1个单位长度的速度从点 A开始沿边 AB 向点 B 运动,动点 F 以每秒2 个单位长度的速度从点 B 开始沿边 BC 向点C 运动，动点 E 比动点 F 先出发1秒,其中一个动点到达终点时，另一个动点也随之停止运动，设点 F 的运动时间为t 秒.  1 如图1，连接 DE , AF ，若 DE AF ，求t 的值  2 如图2 ，连接 ,EF DF ，当t 为何值时， ?EBF DCF 【答案】（1）t=1;(2) 当t 为 9 57 2  秒时， EBF DCF 【解析】（1）利用正方形的性质及条件，得出 ABF DAE≌ ，由 BF=AE，列出方程解方程即 可 （2） EBF DCF ，得到 EB BF DC CF  ，用 t 表示出 BF、AE、FC、BE 列出方程解方程即可， 最后对 t 的取值进行取舍 【详解】解： 1 四边形 ABCD是正方形 , 90AB AD ABF DAE       90ADE AED     DE AF 90BAF AED     BAF ADE   ABF DAE ≌ 由题意得， 2 , 1BF t AE t   2 1t t   解得： 1t   2 若 EBF DCF 则 EB BF DC CF  1, 2AE t BF t   4 1 3BE t t      ， 4 2CF t  3 2 4 4 2 t t t    解得 1 2 9 57 9 57,2 2t t   由题意知： 2t  9 57 2t   当t 为 9 57 2  秒时， EBF DCF 【点睛】本题考查正方形基本性质、全等三角形的判定与性质、相似三角形的判定与性质，第 二问的关键在于能够写出比例式列出方程，最后要记得对方程的解进行取舍 【变式 4-1】已知：如图，在平面直角坐标系中，△ABC 是直角三角形，∠ACB＝90°，点 A，C 的坐标分别为 A（﹣3，0），C（1，0），BC＝ 3 4 AC （1）求过点 A，B 的直线的函数表达式； （2）在 x 轴上找一点 D，连接 DB，使得△ADB 与△ABC 相似（不包括全等），并求点 D 的 坐标； （3）在（2）的条件下，如 P，Q 分别是 AB 和 AD 上的动点，连接 PQ，设 AP＝DQ＝m， 问是否存在这样的 m，使得△APQ 与△ADB 相似？如存在，请求出 m 的值；如不存在，请 说明理由． 【答案】（1）y＝ 3 4 x+ 9 4 ；（2）D 点位置见解析，D（13 4 ，0）；（3）符合要求的 m 的值为125 36 或 25 9 ． 【解析】（1）先根据 A（−3，1），C（1，0），求出 AC 进而得出 BC＝3 求出 B 点坐标，利 用待定系数法求出直线 AB 的解析式即可； （2）运用相似三角形的性质就可求出点 D 的坐标； （3）由于△APQ 与△ADB 已有一组公共角相等，只需分△APQ∽△ABD 和△APQ∽△ADB 两种情况讨论，然后运用相似三角形的性质建立关于 m 的方程，就可解决问题． 【详解】解：（1）∵A（﹣3，0），C（1，0）， ∴AC＝4， ∵BC＝ 3 4 AC， ∴BC＝ 3 4 ×4＝3， ∴B（1，3）， 设直线 AB 的解析式为 y＝kx+b， ∴ 3 0 3 k b k b       ， ∴ 3 4 9 4 k b     ， ∴直线 AB 的解析式为 y＝ 3 4 x+ 9 4 ； （2）若△ADB 与△ABC 相似，过点 B 作 BD⊥AB 交 x 轴于 D， ∴∠ABD＝∠ACB＝90°，如图 1， 此时 AB AC ＝ AD AB ，即 AB2＝AC•AD． ∵∠ACB＝90°，AC＝4，BC＝3， ∴AB＝5， ∴25＝4AD， ∴AD＝ 25 4 ， ∴OD＝AD﹣AO＝ 25 4 ﹣3＝13 4 ， ∴点 D 的坐标为（13 4 ，0）； （3）∵AP＝DQ＝m， ∴AQ＝AD﹣QD＝ 25 4 ﹣m． Ⅰ、若△APQ∽△ABD，如图 2， 则有 AP AB ＝ AQ AD ， ∴AP•AD＝AB•AQ， ∴ 25 4 m＝5（ 25 4 ﹣m）， 解得 m＝ 25 9 ； Ⅱ、若△APQ∽△ADB，如图 3， 则有 AP AD ＝ AQ AB ， ∴AP•AB＝AD•AQ， ∴5m＝ 25 4 （ 25 4 ﹣m）， 解得：m＝125 36 ， 综上所述：符合要求的 m 的值为125 36 或 25 9 ． 【点睛】此题是相似形综合题，主要考查了是待定系数法，相似三角形的判定与性质、勾股定 理等知识，也考查了分类讨论的数学思想，属于中档题，解本题的关键是根据相似建立方程求 解． 【变式 4-2】如图，已知抛物线 2y ax bx c   经过 A（－3，0）、B（8，0）、C（0，4）三点， 点 D 是抛物线上的动点，连结 AD 与 y 轴相交于点 E，连结 AC，CD． （1）求抛物线所对应的函数表达式； （2）当 AD 平分∠CAB 时． ①求直线 AD 所对应的函数表达式； ②设 P 是 x 轴上的一个动点，若△PAD 与△CAD 相似，求点 P 的坐标． 【答案】（1） 21 5 46 6y x x    ；（2）① 1 3 2 2y x  ；②（2，0）或（13，0）． 【解析】（1）将  3 0A  , 、  8,0B 、  0,4C 点坐标代入抛物线 2y ax bx c   ，化简计算即可； （2）① 设  0,E t ，根据 AD 平分 CAB ，EH AC ，EO x 轴，求得 5AC  ，并证得 CHE ∽ COA ，利用 A EH OA CE C  可的 3 2t  ，可得 E 点坐标，把  3 0A  , ， 30, 2E      代入 y kx b  ，化简 可得 AD 所对应的函数表达式； ② 因为 P 是 x 轴上的一个动点，且 PAD△ 与 CAD 相似，并且 ACD是腰长为 5 的等腰三角 形，所以 P 点有两种情况：AD 为等腰三角形的斜边，或者以 AD 为腰， 2P A 为底，分别讨论 求解即可. 【详解】解（1）∵抛物线经过  3 0A  , 、  8,0B 、  0,4C 三点， ∴ 9 3 0 64 8 0 4 a b c a b c c          ，解得： 1 6 5 6 4 a b c         ， ∴抛物线的表达式为 21 5 46 6y x x    ； （2）① 作 EH AC 于点 H，如图，设  0,E t ． ∵ AD 平分 CAB ， EH AC ， EO x 轴， ∴ EH EO t  ， 4CE t  ， 在 Rt OAC△ 中， 2 2 2 23 4 5AC OA OC     ． ∵ 90CHE COA     HCE OCA   ， ∴ CHE ∽ COA ， ∴ A EH OA CE C  ∴ 4 3 5 t t ，解得： 3 2t  ， ∴ 30, 2E      ，设直线 AD 的表达式为 y kx b  ， 把  3 0A  , ， 30, 2E      代入， 得 0 3 3 2 k b b     ，解得： 1 2 3 2 k b     ， ∴直线 AD 所对应的函数表达式为 1 3 2 2y x  ； ② 直线 AD 与二次函数相交于点 D， ∴ 21 5 46 6 1 3 2 2 y x x y x         解得 3 0 x y     或 5 4 x y    ， 点 D 在第一象限， ∴点 D 坐标为 5,4 ， ∴ 5DC AC  ，且 DC AB∥ ， ∴ ACD是腰长为 5 的等腰三角形， P 是 x 轴上的一个动点，且 PAD△ 与 CAD 相似， ∴ PAD△ 也为等腰三角形， 如上图示， 当 AD 为等腰三角形的斜边时， 1 1 5PA PD  ，  3,0A  ∴点 1P 的坐标为 2,0 ； 当以 AD 为腰， 2P A 为底时，作 2DF AP 点 D 坐标为 5,4 ，  3 0A  , ∴ 3 5 8AF OA OF     ∴ 2 2 16AP AF  , 2 2 16 3 13OP AP OA     , ∴点 P 的坐标为 13,0 ． 综上所述点 P 的坐标为 2,0 或 13,0 ． 【点睛】本题考查了二次函数综合题：熟练掌握二次函数图象上点的坐标特征和角平分线的性 质；会利用待定系数法求二次函数和一次函数解析式；灵活利用相似比表示线段之间的关系； 理解坐标与图形性质． 【考点 5】动点之平行四边形问题（含特殊四边形） 【例 5】（2019·广东中考模拟）如图，点 O 是平面直角坐标系的原点，点 A（ 3 ，3），AC⊥OA 与 x 轴的交点为 C．动点 M 以每秒 3 个单位长度由点 A 向点 O 运动．同时，动点 N 以每秒 3 个单位长度由点 O 向点 C 运动，当一动点先到终点时，另一动点立即停止运动． （1）写出∠AOC 的值； （2）用 t 表示出四边形 AMNC 的面积； （3）求点 P 的坐标，使得以 O、N、M、P 为顶点的四边形是特殊的平行四边形？ 【答案】（1）30°；（2） 296 3 (0 2)4 t t   ；（3） 3 3 3P 3t t, t2 2       . 【解析】（1）如图 1 中，作 AH⊥OC 于 H．在 Rt△AOH 中，解直角三角形求出∠AOH 即可 解决问题． （2）作 MK⊥BC 于 K．根据 S 四边形 AMNC＝S△OAC﹣S△OMN，计算即可． （3）分别考虑以 OM，ON，MN 为平行四边形的对角线，利用平行四边形的性质求解即可． 【详解】解：（1）如图 1 中，作 AH⊥OC 于 H． ∵A（ 3 ，3）， ∴OH＝ 3 ，AH＝3， ∴tan∠AOH＝ AH OH ＝ 3 ， ∴∠AOH＝60°， ∵OA⊥AC， ∴∠OAC＝90°， ∴∠ACO＝30°． （2）作 MK⊥BC 于 K． 在 Rt△AOH 中，∵OH＝ 3 ，∠OAH＝30°， ∴OA＝2OH＝2 3 ， 在 Rt△AOC 中，∵∠AOC＝30°，OA＝2 3 ， ∴AC＝ 3 OA＝6， ∵OM＝ 3 t， ∴MK＝OM•sin60°＝ 3 2 t， ∴S 四边形 AMNC＝S△OAC﹣S△OMN ＝ 1 2 •OA•AC﹣ 1 2 •ON•MKa ＝ 1 2 ×2 3 ×6﹣ 1 2 ×3t× 3 2 t ＝6 3 ﹣ 9 4 t2（0＜t＜2）． （3）当四边形 CNMP1 是平行四边形时，P1（ 3 2 t﹣3t， 3 2 t）． 当四边形 ONP2M 是平行四边形时，P2（ 3 2 t+3t， 3 2 t）． 当四边形 OMNP3 是平行四边形时，P3（3t﹣ 3 2 t，﹣ 3 2 t）． 【点睛】本题属于四边形综合题，考查了四边形的面积，平行四边形的性质，解直角三角形等 知识，解题的关键是熟练掌握基本知识，学会用分类讨论的思想思考问题，属于中考常考题型． 【变式 5-1】（2019·江西中考真题）在图 1，2，3 中，已知 ， ，点 为线 段 上的动点，连接 ，以 为边向上作菱形 ，且 ． （1）如图 1，当点 与点 重合时， ________°； （2）如图 2，连接 ． ①填空： _________ （填“>”，“<”，“=”）； ②求证：点 在 的平分线上； （3）如图 3，连接 ， ，并延长 交 的延长线于点 ，当四边形 是平行四边形时， 求 的值． 【答案】（1）60°；（2）① =，②见解析；（3）4 【解析】（1）根据菱形的性质计算； （2）①证明 ，根据角的运算解答； ②作 于 ， 交 的延长线于 ，证明 ，根据全等三角形的性质得 到 ，根据角平分线的判定定理证明结论； （3）根据直角三角形的性质得到 ，证明四边形 为菱形，根据菱形的性质计算， 得到答案． 【详解】解：（1） 四边形 是菱形， ， ， 故答案为： ； （2）① 四边形 是平行四边形， ， 四边形 是菱形， ， ， ， 故答案为： ； ②作 于 ， 交 的延长线于 ， 则 ， ，又 ， ， ， ， 为等边三角形， ， 在 和 中， ， ， ，又 ， ， 点 在 的平分线上； （3） 四边形 是菱形， ， ， ， 四边形 为平行四边形， ， ， ， ，又 ， ， ， ， ， ， 四边形 为平行四边形， ， ， 四边形 为平行四边形， ， 平行四边形 为菱形， ， ， ． 【点睛】本题考查了菱形的性质、平行四边形的性质、全等三角形的判定和性质.掌握全等三 角形的判定定理和性质定理、菱形的性质、直角三角形的性质是解题的关键． 【变式 5-2】（2019·湖南中考真题）如图，二次函数 21 3y x bx c    的图象过原点，与 x 轴 的另一个交点为 8,0 （1）求该二次函数的解析式； （2）在 x 轴上方作 x 轴的平行线 1y m ，交二次函数图象于 A、B 两点，过 A、B 两点分别作 x 轴的垂线，垂足分别为点 D、点 C．当矩形 ABCD 为正方形时，求 m 的值； （3）在（2）的条件下，动点 P 从点 A 出发沿射线 AB 以每秒 1 个单位长度匀速运动，同时 动点 Q 以相同的速度从点 A 出发沿线段 AD 匀速运动，到达点 D 时立即原速返回，当动点 Q 返回到点 A 时，P、Q 两点同时停止运动，设运动时间为 t 秒（ 0t  ）．过点 P 向 x 轴作垂线， 交抛物线于点 E，交直线 AC 于点 F，问：以 A、E、F、Q 四点为顶点构成的四边形能否是平 行四边形．若能，请求出 t 的值；若不能，请说明理由． 【答案】（1） 21 8 3 3y x x   ；（2）当矩形 ABCD 为正方形时，m 的值为 4；（3）以 A、E、F、 Q 四点为顶点构成的四边形能为平行四边形，t 的值为 4 或 6. 【解析】（1）根据点的坐标，利用待定系数法即可求出二次函数的解析式； （2）利用二次函数图象上点的坐标特征求出点 A，B 的坐标，进而可得出点 C，D 的坐标， 再利用正方形的性质可得出关于 m 的方程，解之即可得出结论； （3）由（2）可得出点 A，B，C，D 的坐标，根据点 A，C 的坐标，利用待定系数法可求出 直线 AC 的解析式，利用二次函数图象上点的坐标特征及一次函数图象上点的坐标特征可求出 点 E，F 的坐标，由 AQ EF 且以 A、E、F、Q 四点为顶点的四边形为平行四边形可得出 AQ EF ， 分0 t 4  ， 4 t 7  ，7 t 8  三种情况找出 AQ，EF 的长，由 AQ EF 可得出关于 t 的一元 二次方程，解之取其合适的值即可得出结论． 【详解】（1）将 0 0， ， 8 0， 代入 21y x bx c3     ，得： 0 64 8 03 c b c     ， 解得 8 3 0 b c     ， ∴该二次函数的解析式为 21 8y x x3 3    ． （2）当 y m 时， 21 8x x m3 3    ， 解得： 1x 4 16 3m   ， 2x 4 16 3m   ， ∴点 a 的坐标为（ 4 16 3m  ，m），点 b 的坐标为（ 4 16 3m  ，m）， ∴点 d 的坐标为（ 4 16 3m  ，0），点 c 的坐标为（ 4 16 3m  ，0）． ∵矩形 abcd 为正方形， ∴  4 16 3m 4 16 3m m      ， 解得： 1m 16  ，（舍去）， 2m 4 ． ∴当矩形 ABCD 为正方形时，m 的值为 4． （3）以 A、E、F、Q 四点为顶点构成的四边形能为平行四边形． 由（2）可知：点 A 的坐标为 2 4， ，点 B 的坐标为 6 4， ，点 C 的坐标为 6 0， ，点 D 的坐标 为 2 0， ． 设直线 AC 的解析式为  y kx a k 0   ， 将  a 2 4， ，  c 6 0， 代入 y kx a  ， 得 2 4 6 0 k a k a      ， 解得 1 6 k a     ， ∴直线 ac 的解析式为 y x 6   ． 当 x 2 t  时， 2 21 8 1 4y x x t t 43 3 3 3        ， y x 6 t 4      ∴点 E 的坐标为（ 2 t ， 21 4t t 43 3    ），点 F 的坐标为（2 t ， t 4  -t+4）． ∵以 A、E、F、Q 四点为顶点构成的四边形为平行四边形，且 AQ ΕF ， ∴ AQ EF ，分三种情况考虑： ①当0 t 4  时，如图 1 所示， AQ t ，EF=  2 21 4 1 7t t 4 t 4 t t3 3 3 3          ， ∴ 21 7t t t3 3    ，解得： 1t 0 （舍去）， 2t 4 ； ②当 4 t 7  时，如图 2 所示， AQ t 4  ，EF=  2 21 4 1 7t t 4 t 4 t t3 3 3 3          ， ∴ 21 7t 4 t t3 3     ， 解得： 3t 2  （舍去）， 4t 6 ； 7 t 8  , AQ t 4  , EF=  2 21 4 1 7t t 4 t 4 t t3 3 3 3          ， 21 7t 4 t t3 3     ， 解得 5t 5 13  （舍去）， 6t 5 13  （舍去） 综上所述，当以 A、E、F、Q 四点为顶点构成的四边形为平行四边形时，t 的值为 4 或 6 【点睛】本题考查了待定系数法求二次函数解析式、二次函数图象上点的坐标特征、正方形的 性质、待定系数法求一次函数解析式、一次函数图象上点的坐标特征以及平行四边形的性质， 解题的关键是：（1）根据点的坐标，利用待定系数法求出二次函数解析式；（2）利用正方形的 性质，找出关于 m 的方程；（3）分0 t 4  ， 4 t 7  ，7 t 8  三种情况，利用平行四边形 的性质找出关于 t 的一元二次方程． 【变式 5-3】．如图，在平面直角坐标系中， AOB 的顶点O是坐标原点，点 A坐标为 1,3 ，A、 B 两点关于直线 y x 对称，反比例函数  0ky xx   图象经过点 A，点 P 是直线 y x 上一动点. （1） B 点的坐标为______； （2）若点C 是反比例函数图象上一点，是否存在这样的点C ，使得以 A、 B 、C 、 P 四点为 顶点的四边形是平行四边形？若存在，求出点C 坐标；若不存在，请说明理由； （3）若点Q 是线段OP 上一点（O不与O、 P 重合），当四边形 AOBP 为菱形时，过点Q 分别 作直线OA和直线 AP 的垂线，垂足分别为 E 、 F ，当QE QF QB  的值最小时，求出Q 点坐 标. 【答案】（1）（3，1）；（2） 1( 7 2, 7 2)C   ， 2 ( 7 2, 7 2)C   ， 3( 3, 3)C ；（3）（2，2）. 【解析】（1）根据点（a，b）关于 y=x 对称的点的坐标为（b，a）直接写出答案即可； （2）首先求得反比例函数的解析式，然后设 P（m，m），分若 PC 为平行四边形的边和若 PC 为平行四边形的对角线两种情况分类讨论即可确定点 C 的坐标； （3）连接 AQ，设 AB 与 PO 的交点为 D，利用四边形 AOBP 是菱形，得到 S△AOP=S△AOQ+S△APQ， 从而得到 1 2 PO•AD= 1 2 AO•QE+ 1 2 AP•QF，确定 QE+QF= •PO AD AO 为定值，从而求解． 【详解】解：（1）B 点的坐标为（3，1）； （2）∵反比例函数  0ky xx   图象经过点 A（1，3）， ∴k=1×3=3， ∴反比例函数的解析式为 3y x  ， 点 P 在直线 y=x 上， ∴设 P（m，m） ①PC 为平行四边形的边， ∵点 A 的横坐标比点 B 的横坐标小 2，点 A 的纵坐标比点 B 的纵坐标大 2， ∴点 C 在点 P 的下方，则点 C 的坐标为（m+2，m-2）如图 1， 若点 C 在点 P 的上方，则点 C 的坐标为（m-2，m+2）如图 2， 把 C（m+2，m-2）代入反比例函数的解析式得： 7m   ， ∵m＞0， ∴ 7m  ， ∴ 1( 7 2, 7 2)C   同理可得另一点 2 ( 7 2, 7 2)C   ， ②若 PC 为平行四边形的对角线，如图 3， ∵A、B 关于 y=x 对称， ∴OP⊥AB 此时点 C 在直线 y=x 上，且为直线 y=x 与双曲线的 3y x  交点， 由 3 y x y x   解得： 1 1 3 3 x y    ， 2 2 3 3 x y      （舍去）， ∴ 3( 3, 3)C ， 综上所述，满足条件的点 C 有三个，坐标分别为： 1( 7 2, 7 2)C   ， 2 ( 7 2, 7 2)C   ， 3( 3, 3)C ； （3）连接 AQ，设 AB 与 PO 的交点为 D，如图 4， ∵四边形 AOBP 是菱形， ∴AO=AP ∵S△AOP=S△AOQ+S△APQ， ∴ 1 2 PO•AD= 1 2 AO•QE+ 1 2 AP•QF ∴QE+QF= •PO AD AO 为定值， ∴要使 QE+QF+QB 的值最小，只需 QB 的值最小，当 QB⊥PO 时，QB 最小， 所以 D 点即为所求的点， ∵A（1，3），B（3，1） ∴D（2，2）， ∴当 QE+QF+QB 的值最小时，Q 点坐标为（2，2）． 【点睛】本题是对反比例函数的综合知识的考查，熟练掌握反比例，四边形知识及分类讨论的 数学思想是解决本题的关键，难度较大． 【考点 6】动点之线段面积问题 【例 6】如图已知平面内有一动点 A，x 轴上有一定点 B（4，0），连接 AB，且将线段 AB 绕 B 点逆时针旋转 90°得到线段 BC． ①当 A 点坐标为（1，1）时，求 C 点坐标； ②当 A 点在直线 x=1 上滑动时，求在此运动过程中△BOC 的面积是否发生变化，若不变，请 求出面积，若变化，请说明理由； ③若总条件中的动点 A 改为直线 y=x 上的动点 A，其余条件都不变，请直接写出当 A 点在直 线 y=x 上滑动时，点 D（0，-2）到 C 点的最短距离． 【答案】（1）C（3，3）；（2）当 A 点在直线 x=1 上滑动时，在此运动过程中△BOC 的面积 是不发生变化，是定值 6；（3）A 点在直线 y=x 上滑动时，点 D（0，-2）到 C 点的最短距离 为 2 ． 【解析】①先判断出△ABD≌△BCE，进而确定出点 C 的坐标； ②同①的方法确定出点 C 的坐标，再利用三角形的面积公式即可得出结论； ③先判断出点 C 是直线 y=-x 上运动，进而确定出 DC 垂直于直线 y=-x 时，CD 最小，最后用 等腰直角三角形的性质即可得出结论． 【详解】①如图①， 过点 A 作 AD⊥x 轴于 D，过点 C 作 CE⊥x 轴于 E， ∴∠ADB=∠BEC=90°， ∴∠BAD+∠ABD=90°， 由旋转知，AB=BC，∠ABC=90°， ∴∠ABD+∠CBE=90°， ∴∠BAD=∠CBE， 在△ABD 和△BCE 中， ADB BEC BAD CBE AB CB      ＝ ＝ ＝ ， ∴△ABD≌△BCE， ∴BD=CE，AD=BE， ∵A（1，1），B（4，0）， ∴AD=1，BD=3， ∴CE=BD=3，BE=AD=1， ∴OE=OB-BE=4-1=3， ∴C（3，3）； ②如图②， 过点 A 作 AD⊥x 轴于 D，过点 C 作 CE⊥x 轴于 E， ∴∠ADB=∠BEC=90°， ∴∠BAD+∠ABD=90°， 由旋转知，AB=BC，∠ABC=90°， ∴∠ABD+∠CBE=90°， ∴∠BAD=∠CBE， 在△ABD 和△BCE 中 90ADB BEC BAD CBE AB CB       ＝ ＝ ＝ ＝ ， ∴△ABD≌△BCE， ∴BD=CE，AD=BE， ∵A 点在直线 x=1 上滑动， ∴设 A（1，m）， 当 m≥0 时，∵B（4，0）， ∴AD=m，BD=3， ∴CE=BD=3，BE=AD=m， ∴OE=|OB-BE|=|4-m|， ∴C（|4-m|，3）， ∴S△BOC= 1 2 OB×|yC|= 1 2 ×4×3=6，是定值； 当 m＜0 时，∵B（4，0）， ∴AD=|m|=-m，BD=3， ∴CE=BD=3，BE=AD=-m， ∴OE=|OB+BE|=|4-m|， ∴C（|4-m|，3）， ∴S△BOC= 1 2 OB×|yC|= 1 2 ×4×3=6，是定值； 即：当 A 点在直线 x=1 上滑动时，在此运动过程中△BOC 的面积是不发生变化，是定值 6； ③如图③， 过点 B 作 BE⊥OA 于 E，过点 B 作 BF⊥BE，过点 C 作 CO'⊥BF 于 F，交 OA 于 O'， ∴∠AEB=∠BFC=∠EBF=90°， ∴四边形 BEO'F 是矩形， 由旋转知，AB=BC，∠ABC=90°， ∴∠ABE=∠CBF， 在△ABE 和△CBF 中， 90AEB CFB ABE CBF AB CB       ＝ ＝ ＝ ＝ ， ∴△ABE≌△CBF， ∴BE=BF， ∵BE⊥OA，BF⊥O'C， ∴点 B 在 AO'C 的角平分线上， ∴点 O'和点 O 重合， ∴∠BOC=45° ∴点 C 在直线 y=-x 上， 过点 D 作 DG⊥OC 于 G， ∴点 C 和点 G 重合时，CD 最小是 CG， 在 Rt△ODG 中，∠DOG=45°，OD=2， ∴DG= 2 ， 即：当 A 点在直线 y=x 上滑动时，点 D（0，-2）到 C 点的最短距离为 2 ． 【点睛】此题是一次函数综合题，主要考查了全等三角形的判定和性质，三角形的面积公式， 角平分线定理，解本题的关键是构造全等三角形. 【变式 6-1】（2019·山东中考模拟）如图，抛物线 2y x bx c    交 x 轴于点  3 0A  , 和点 B ， 交 y 轴于点  0,3C . （1）求抛物线的函数表达式； （2）若点 P 在抛物线上，且 4AOP BOCS S  ，求点 P 的坐标； （3）如图，设点Q是线段 AC 上的一动点，作 DQ x 轴，交抛物线于点 D ，求线段 DQ 长度 的最大值，并求出 DAC 面积的最大值. 【答案】（1） 2 2 3y x x    ；（2）符合条件的点 P 的坐标为： 1,4 或 1 2 2, 4   或  1 2 2, 4   ；（3） DAC 面积的最大值为 27 8 . 【解析】（1）把点 A、C 的坐标分别代入函数解析式，列出关于系数的方程组，通过解方程组 求得系数的值； （2）设 P 点坐标为（x，-x2-2x+3），根据 S△AOP=4S △BOC 列出关于 x 的方程，解方程求出 x 的 值，进而得到点 P 的坐标； （3）先运用待定系数法求出直线 AC 的解析式为 y=x+3，再设 Q 点坐标为（x，x+3），则 D 点坐标为（x，-x2-2x+3），然后用含 x 的代数式表示 QD，根据二次函数的性质即可求出线段 QD 长度的最大值,再根据 DAC DAQ DCQS S S    求得最大面积． 【详解】（1）把  3 0A  , ，  0,3C 代入 2y x bx c    ，得 0 9 3 3 b c c       ，解得 2 3 b c     . 故该抛物线的解析式为： 2 2 3y x x    . （2）由（1）知，该抛物线的解析式为 2 2 3y x x    ，则易得  10B , . 设 P 点坐标为（x，-x2-2x+3）， ∵ 4AOP BOCS S  ， ∴ 21 13 2 3 4 1 32 2x x         . 整理，得 21 0x   或 2 2 7 0x x   ， 解得 1x   或 1 2 2x    . 则符合条件的点 P 的坐标为： 1,4 或 1 2 2, 4   或 1 2 2, 4   ； （3）设直线 AC 的解析式为 y kx t  ，将  3 0A  , ，  0,3C 代入， 得 3 0 3 k t t      ， 解得 1 3 k t    . 即直线 AC 的解析式为 3y x= + . 设Q点坐标为 , 3x x  ， 3 0x   ，则 D 点坐标为 2, 2 3x x x   ，     2 2 2 3 93 3 3 2 4QD x x x x x x                ， ∴当 3 2x   时，QD 有最大值 9 4 . 此时， 21 3 9 1 9 273 + + 3 =2 2 4 2 4 8DAC DAQ DCQS S S x                   ∴ DAC 面积的最大值为 27 8 . 【点睛】考查了待定系数法求二次函数、一次函数的解析式，二次函数的性质以及三角形面积、 线段长度问题．此题难度适中，解题的关键是运用方程思想与数形结合思想． 【变式 6-2】如图，矩形 ABCD中， 3, 4AD AB  ，点 P 是对角线 AC 上一动点（不与 A C、 重 合），连接 PB ，过点 P 作 PE PB ，交射线 DC 于点 E ，以线段 ,PE PB 为邻边作矩形 BPEF ， 过点 P 作GH CD 。分别交 AB CD、 于点G H、 。 （1）求证： PGB EHP  的值； （2）求 PE PB 的值； （3）求矩形 BPEF 的面积的最小值。 【答案】（1）见解析；（2） 3 4 PE PB  ；（3）108 25 . 【解析】(1)根据矩形的性质和同角的余角相等证明 090EHP PGB    ， EPH GBP   ， 从而求证三角形相似；（2）设 AG a ，由相似三角形对应边成比例列出比例式 AG GP CH PH  ，  3 4 34 4 4 aPE PH PB BG a     ，从而求解；（3）当 PB AC 时，矩形 BPEF 面积最小，从而求解. 【详解】（1） ∵过点 P 作 PE PB 且矩形 ABCD中，AB∥DC 又∵过点 P 作 PE PB ∴ 90 , 90EPH GPB GBP GPB         ∴ 090EHP PGB    ， EPH GBP   ∴ PGB EHP  ； （2）设 AG a ，则 4BG CH a   ， ∵矩形 ABCD中，AB∥DC ∴△APG∽△CPH 即∴ AG GP CH PH  ，即 3 4 a PH a PH  ∴  3 44PH a  ∵ PGB EHP  ∴  3 4 34 4 4 aPE PH PB BG a     ； （3）如图∵ 3 4 PE PB  ， ∴当 PB AC 时，矩形 BPEF 面积最小，此时 12 5 CB ABBP AC   ， 此时点 E 与点C 重合， 3 9 4 5PE PC PB   ，所以最小面积为 9 12 108 5 5 25   【点睛】本题考查相似三角形综合题、矩形的性质、相似三角形的判定和性质、勾股定理,解 题的关键是学会利用相似三角形的判定和性质列出相应的比例式从而解决问题． 【变式 6-2】已知：在四边形 ABCD中， AD BC∥ ， 5AB CD  ， 6AD  ， 12BC  ． （1）求四边形 ABCD的面积． （ 2 ）点 P 是线段 AD 上的动点，连接 BP 、CP ，求 BCP 周长的最小值及此时 AP 的长． （3 ）点 P 是线段 AD 上的动点，N 、M 为边 BC 上的点， 5BM CN  ，连接 AN 、DM，分 别交 BP 、CP 于点 E 、 F ，记 ADG 和 BPC△ 重叠部分的面积为 S ，求 S 的最值． 【答案】（1）36．（ 2 ） min 4 13 12C   ．3．（3 ） 45 13 ． 【解析】 试题分析：（1）如图 1，过 A 作 AE⊥BC 于 E，DF⊥BC 于 F，得到四边形 AEFD 是矩形，由 矩形的想知道的 EF=AD=6，BE=CF=3，根据勾股定理得到 2 2 2 25 3 4AE AB BE     ， 于是得到结论； （2）如图2，作点B关于直线AD的对称点G，连接CG交AD于P，则BC+PB+PC=BC+PG+PC 即为△BCP 周长的最小值，根据勾股定理得到 2 2 2 212 8 4 13CG BC BG     ，于是得 到△BCP 周长的最小值为：4 13 +12；根据三角形中位线的性质得到 PH= 1 2 BC=6，由勾股定 理得到 2 2 3AH AB BH   ，于是得到结论． （3）过 E 点作 BC 的垂线分别交 AD 、BC 于G 、H 点，过 F 点作 BC 的垂线分别交 AD 、BC 于 I 、 J 点，过G 点作 BC 的垂线分别交 AD 、 BC 于 K 、 L 点，如图所示，设 AP x ，则 6PD x  ．因为 AD DC ，所以 AGD△ ∽ NGM△ ，得 1GL  ；同理可得 AEP△ ∽ NEB ， DFP ∽ MFC ，得： 28 7EH x   ， 28 13FJ x   ，所以 PBC EBN FMC MGNS S S S S    ，进而求 得答案. 试题解析：（1）如图 1，过 A作 AE BC 于 E ， DF BC 于 D ． 则四边形 AEFD 是矩形． ∴ 6EF AD  ， 3BE CF  ． ∴ 2 2 2 25 3 4AE AB BE     ． ∴ 1 1( ) (6 12) 4 362 2ABCDS AD BC AE四         ． （ 2 ）如图 2，作点 B 关于直线 AD 的对称点G ， 连接 CG 交 AD 于 P ，则 BC PB PC BC PG PC     ． 即为 BCP 的最小周长． 由（1）知 8( 2 )BG AE  ． 在 Rt GBC 中， 2 2 2 212 8 4 13CG BC BG     ． ∴ BCP 的 min 4 13 12C   ． ∵ AD BC∥ ， BH HG ， ∴ 1 62PH BC  ． ∵ 2 2 3AH AB BH   ， ∴ 3AP PH AH   ． （3 ）过 E 点作 BC 的垂线分别交 AD 、BC 于G 、H 点，过 F 点作 BC 的垂线分别交 AD 、BC 于 I 、 J 点，过G 点作 BC 的垂线分别交 AD 、 BC 于 K 、 L 点，如图 3 所示，设 AP x ，则 6PD x  ． 因为 AD DC ，所以 AGD△ ∽ NGM△ ， 所以 6 2 GK AD GL MN   ，又 4KL  ，所以 1GL  ； 同理可得 AEP△ ∽ NEB ， DFP ∽ MFC ， 所以 7 GE AP x HE BN   ， 6 7 IF PD x JF MC   ， 求得： 28 7EH x   ， 28 13FJ x   ，其中0 6x  ， 所以 PBC EBN FMC MGNS S S S S    ， 即 1 1 28 1 28 112 4 7 7 2 12 2 7 2 13 2S x x              2 19625 ( 3) 100x      ． 因此当 3x  时， S 有最大值6.4 ；当 0x  或 6x  时， S 有最小值了 45 13 ． 【达标训练】 一、单选题 1．如图，在△ABC 中，AB=2，AO=BO，P 是直线 CO 上的一个动点，∠AOC=60°，当 △PAB 是以 BP 为直角边的直角三角形时，AP 的长为（ ） A． 5 ,1,2 B． 2 , 7 ,2 C． 3 , 7 ,1 D． 10 ，2 【答案】C 【解析】利用分类讨论，分当∠ABP=90°时和当∠APB=90°时两种情况讨论即可． 【详解】当∠APB=90°时, 情况一：（如图）， ∵AO=BO， ∴PO=BO， ∵∠AOC=60°， ∴∠BOP=60°， ∴△BOP 为等边三角形， ∴BP=1， 在 Rt△APB 中，AP= 2 2 2 22 1 3AB BP    ； 情况二：如图 2， ∵AO=BO，∠APB=90°， ∴PO=AO， ∵∠AOC=60°， ∴△AOP 为等边三角形， ∴AP=AO=1； 当∠ABP=90°时（如图 3）， ∵∠AOC=∠BOP=60°， ∴∠BPO=30°， ∴OP=2OA=2， ∴BP= 2 2 2 22 1 3OP OB    ， 在直角三角形 ABP 中， AP= 2 2 2 22 ( 3) 7AB BP    ； 故选：C． 【点睛】本题主要考查了勾股定理，含 30°直角三角形的性质和直角三角形斜边的中线，分 类讨论，数形结合是解答此题的关键． 2．如图，在矩形 ABCD 中，AB=5，AD=3，动点 P 在直线 AB 上方，且满足 S△PABS：矩形 ABCD=1： 3，则使△PAB 为直角三角形的点 P 有( )个 A．1 B．2 C．3 D．4 【答案】D 【解析】分当点 P 在 AD 上时，则 90PAB   ；当点 P 在 BC 上时，则 90 ;PBA   当点 P 在矩形 ABCD 内部时，则 90 ,APB   三种情况进行讨论. 【详解】四边形 ABCD 为矩形.  90 ,DAB CBA     S 矩形 ABCD 5 3 15,AB AD      S△PAB：S 矩形 ABCD=1：3， 1 15 5,3PABS    当点 P 在 AD 上时，则 90 ,PAB   1 5,2 AB PA   即 1 5 5,2 PA   2,PA  故点 P 在 AD 上且 2PA  时，△PAB 为直角三角形. 当点 P 在 BC 上时，则 90 ,PBA   1 5,2 AB PB   即， 1 5 5,2 PB   2,PB  故点 P 在 BC 上且 2PB  时，△PAB 为直角三角形. 当点 P 在矩形 ABCD 内部时，则 90 ,APB   作 PE AB 于点 E，如图所示. 1 5,2 AB PE   即 1 5 5,2 PE   2,PE  由 90 ,APB   PE AB 可知： ,APE PBE∽ ,PE BE AE PE   2 4,AE BE PE    设 AE x ，则 5 ,BE x  .  5 4,x x   解得： 1 21, 4,x x   1AE  或 4,AE  在矩形 ABCD 内部时，符合条件的点 P 有 2 个. 综上所述，符合条件的点 P 共有 4 个. 故选：D. 【点睛】考查矩形的性质，相似三角形的判定与性质，三角形的面积公式，解一元二次方程等， 注意分类讨论思想在解题中的应用. 3．已知抛物线 21 14y x  具有如下性质:抛物线上任意一点到定点  0,2F 的距离与到 x 轴的距 离相等.如图点 M 的坐标为 3,6 , P 是抛物线 21 14y x  上一动点，则 PMF 周长的最小值是 （ ） A．5 B．9 C．11 D．1 【答案】C 【解析】作过 P 作 PH x 轴于点 H ，过点 M 作 MH x 轴于点 'H ，交抛物线 21 14y x  于点 P ，由 PF PH 结合，结合点到直线之间垂线段最短及 MF 为定值，即可得出当点 P 运动到 点 P′时，△PMF 周长取最小值，再由点 F 、 M 的坐标即可得出 MF 、 MH 的长度，进而得 出 PMF 周长的最小值． 【详解】解：作过 P 作 PH x 轴于点 H ， 由题意可知： PF PH ， ∴ PMF 周长= MF MP PF MF MP PH     ， 又∵点到直线之间垂线段最短， ∴当 M 、 P 、 H 三点共线时 MP PH 最小，此时 PMF 周长取最小值， 过点 M 作 MH x 轴于点 H ，交抛物线 21 14y x  于点 P ，此时 PMF 周长最小值， (0,2)F 、 (3,6)M ， ' 6MH  ， 2 2(3 0) (6 2) 5FM      ， PMF 周长的最小值 6 5 11ME FM     ． 故选：C ． 【点睛】本题考查了二次函数的性质、二次函数图象上点的坐标特征以及点到直线的距离，根 据点到直线之间垂线段最短找出△PMF 周长的取最小值时点 P 的位置是解题的关键． 二、填空题 4．如图,四边形 ABCD 中,AB∥CD,∠B=90°,AB=1,CD=2,BC=3,点 P 为 BC 边上一动点,若 △PAB 与△PCD 是相似三角形,则 BP 的长为 _____________ 【答案】1 或 2 【解析】设 BP=x，则 CP=BC－BP=3－x，易证∠B=∠C=90°，根据相似三角形的对应顶点 分类讨论：①若△PAB∽△PDC 时，列出比例式即可求出 BP；②若△PAB∽△DPC 时，原理 同上. 【详解】解：设 BP=x，则 CP=BC－BP=3－x ∵AB∥CD,∠B=90°, ∴∠C=180°－∠B=90° ①若△PAB∽△PDC 时 ∴ AB BP CD CP  即 1 2 3 x x   解得：x=1 即此时 BP=1； ②若△PAB∽△DPC 时 ∴ AB BP PC CD  即 1 3 2 x x  解得： 1 21, 2x x  即此时 BP=1 或 2； 综上所述：BP=1 或 2. 故答案为：1 或 2. 【点睛】此题考查的是相似三角形的判定及性质，掌握相似三角形的对应边成比例列方程是解 决此题的关键. 5．如图，AB BC 于 B , DC BC 于C , 6, 8, 2AB BC CD   ，点 P 为 BC 边上一动点，当 BP ＝________时，形成的 Rt ABP 与 Rt PCD 全等. 【答案】2 【解析】当 BP=2 时，Rt△ABP≌Rt△PCD，由 BC=8 可得 CP=6，进而可得 AB=CP，BP=CD， 再结合 AB⊥BC、DC⊥BC 可得∠B=∠C=90°，可利用 SAS 判定△ABP≌△PCD． 【详解】当 BP=2 时，Rt△ABP≌Rt△PCD．理由如下： ∵BC=8，BP=2， ∴PC=6， ∴AB=PC． ∵AB⊥BC，DC⊥BC， ∴∠B=∠C=90°． 在△ABP 和△PCD 中，∵ 6 90 2 AB PC B C BP CD           ， ∴△ABP≌△PCD(SAS)． 故答案为：2． 【点睛】本题考查了直角三角形全等的判定方法，关键是掌握 SAS 定理． 6．如图，矩形 ABCD中， 3AB  ， 4BC  ，点 P 是对角线 AC 上一动点，过点 P 作 PE AD 于 点 E ，若点 P ， A， B 构成以 AB 为腰的等腰三角形时，则线段 PE 的长是__________． 【答案】 9 5 或 54 25 【解析】由勾股定理得求出 5AC  ，分 PA AB 与 PB AB 两种情况分别讨论计算即可. 【详解】解：∵矩形 ABCD中， 3AB  ， 4BC  ∴由勾股定理得 2 23 4 5AC    ，分两种情况： （1）如图，当 3PA AB  时， ∵ PE AD ， ∴ 90PEA D     ， ∴ / /PE CD， ∴ APE ∽ ACD ， ∴ PE AP CD AC  ， 3 3 5 PE  ， ∴ 9 5PE  ； （2）如图，当 PB AB 时，过点 B 作 BM AC 于点 M ， ∵∠BAC=∠BAM,∠ABC=∠BMA=90° ∴ ABM ∽ ACB ， ∴ AB AM AC AB  ， 3 5 3 AM ， ∴ 9 5AM  ， ∵ AB PB ， ∴ 182 5AP AM  ， 由（1）得 APE ∽ ACD ， ∴ PE AP CD AC  ， 18 5 3 5 PE  ， ∴ 54 25PE  ， 综上， PE 的值为 9 5 或 54 25 . 【点睛】本题主要考查了勾股定理的应用、矩形的性质以及相似三角形的性质，熟练掌握各个 知识点并学会运用是解题的关键. 7．如图，在矩形OAHC 中， 8 , 12OC OA  ， B 为CH 中点，连接 AB . 动点 M 从点O出发 沿OA边向点 A运动，动点 N 从点 A出发沿 AB 边向点 B 运动，两个动点同时出发，速度都是 每秒 1 个单位长度，连接 , ,CM CN MN ，设运动时间为t （秒）(0 10)t  . 则t  _____时， CMN 为直角三角形 【答案】 7 2 或 41 241 4  【解析】△CMN 是直角三角形时，有三种情况，一是∠CMN=90°，二是∠MNC=90°，三 是∠MCN=90°，然后进行分类讨论求出 t 的值． 【详解】解： 过点 N 作 OA 的垂线，交 OA 于点 F，交 CH 于点 E，如图 1， ∵B 点是 CH 的中点， ∴BH= 1 2 CH= 1 2 OA=6， ∵AH=OC=8， ∴由勾股定理可求：AB=10， ∵AN=t， ∴BN=10-t， ∵NE∥AH， ∴△BEN∽△BHA， ∴ BN EN AB AH  ， ∴10 10 8 t EN  ， ∴EN= 4(10 ) 5 t ∴FN=8-EN= 4 5 t ， 当∠CMN=90°， 由勾股定理可求：AF= 3 5 t ， ∵OM=t， ∴AM=12-t， ∴MF=AM-AF=12-t- 3 5 t =12- 8 5t ， ∵∠OCM+∠CMO=90°，∠CMO+∠FMN=90°， ∴∠OCM=∠FMN， ∵∠O=∠NFM=90°， ∴△COM∽△MFN， ∴ OC OM MF FN  ， ∴ 8 8 412 5 5 t t t   ， ∴t= 7 2 ， 当∠MNC=90°， FN= 4 5 t ∴EN= 48- 5 t ∵MF=12- 8 5t ∴CE=OF=OM+MF=12- 3 5 t ∵∠MNF+∠CNE=90°， ∠ECN+∠CNE=90°， ∴∠MNF=∠ECN， ∵∠CEN=∠NFM=90°， ∴△CEN∽△NFM， ∴ CE EN FN MF  ， ∴ 3 412 8-5 5 4 8125 5 t t t t    ， ∴ 41 241 4t  ， ∵0＜t＜5， ∴ 41 241 4t  ； 当∠NCM=90°， 由题意知：此情况不存在， 综上所述，△CMN 为直角三角形时，t= 7 2 或 41 241 4  . 【点睛】本题主要考查了相似三角形的判定与性质、勾股定理等知识，有一定的综合性． 8．如图，在 ABC 中，已知 4AB AC  ， 6BC  ，P 是 BC 边上的一动点（ P 不与点 B 、C 重 合）.连接 AP ， B APE   ，边 PE 与 AC 交于点 D ，当 APD 为等腰三角形时，则 PB 之长 为_________. 【答案】2 或10 3 【解析】分别讨论 AP=PD、PD=AD、PA=AD 三种情况，当 AP=PD 时，可证明△APB≌△ PDC，可得 PC=AB，进而可求出 PB 的长；当 PD=AD 时，可证明△APC∽△BAC，根据相 似三角形的性质即可求出 PC 的长，进而可得 PB 的长；当 PA=AD 时，P 点与点 B 重合，不 符合题意；综上即可得答案. 【详解】①当 AP=PD 时， ∵∠APC=∠APD+∠DPC=∠B+∠BAP，∠B=∠APD， ∴∠DPC=∠BAP， ∵AB=AC， ∴∠B=∠C， ∵∠B=∠C，∠DPC=∠BAP，AP=PD， ∴△APB≌△PDC， ∴PC=AB=4， ∴PB=BC-PC=2， ②当 PD=AD 时， ∵AD=PD，∠APD=∠B， ∴∠APD=∠PAD=∠B， ∵∠PAD=∠B，∠C=∠C， ∴△APC∽△BAC， ∴ PC AC AC BC  ，即 4 4 6 PC  ， 解得：PC= 8 3 ， ∴PB=BC-PC=10 3 . ③当 PA=AD 时，P 点与点 B 重合，不符合题意； 综上所述：PB 的长为 2 或10 3 . 故答案为：2 或10 3 【点睛】本题考查全等三角形的判定与性质及相似三角形的判定与性质，熟练掌握判定定理及 性质并运用分类思想是解题关键. 9．如图，抛物线 y=﹣ 1 2 x2+mx+n 与 x 轴交于 A、B 两点，与 y 轴交于点 C，抛物线的对称 轴交 x 轴于点 D，已知 A（﹣1，0），C（0，2），点 E 是线段 BC 上的一个动点，过点 E 作 x 轴的垂线与抛物线相交于点 F，当四边形 CDBF 的面积最大时，E 点的坐标为_____． 【答案】（2，1） 【解析】由于四边形 CDBF 的面积等于△CDB 的面积与△BCF 的面积之和，当四边形 CDBF 的面积最大时，即△BCF 最大，设点 E 的坐标为（x，y），利用点 E 的坐标表示出△BCF 的面 积即可求出点 E 的坐标． 【详解】过点 E 作 EG⊥x 轴于点 G，交抛物线于 F， 将 A（﹣1，0），C（0，2）代入 y=﹣ 1 2 x2+mx+n 2 1 ( ) 02 n m n      解得： 3 2 2 m n     ∴抛物线的解析式为：y=﹣ 1 2 x2+ 3 2 x+2 令 y=0 代入 y=﹣ 1 2 x2+ 3 2 x+2， ∴0=﹣ 1 2 x2+ 3 2 x+2 解得：x=﹣1 或 x=4 ∴B（4，0） ∴OB=4 设直线 BC 的解析式为 y=kx+b， 把 B（4，0）和 C（0，2）代入 y=kx+b ∴ 0 4 2 k b b     解得： 1 2 2 k b      ∴直线 BC 的解析式为：y=﹣ 1 2 x+2， 设 E 的坐标为：（x，﹣ 1 2 x+2） ∴F（x，﹣ 1 2 x2+ 3 2 x+2） ∴EF=﹣ 1 2 x2+ 3 2 x+2﹣（﹣ 1 2 x+2）=﹣ 1 2 x2+2x， ∴△BCF 的面积为： 1 2 EF•OB=2（﹣ 1 2 x2+2x）=﹣x2+4x=﹣（x﹣2）2+4 四边形 CDBF 的面积最大时，只需要△BCF 的面积最大即可， ∴当 x=2 时， △BCF 的面积可取得最大值， 此时 E 的坐标为（2，1） 故答案是：(2,1). 【点睛】考查二次函数的综合问题，解题的关键是求出△BCF 的面积的表达式. 10．如图，直线 PQ 经过 Rt ABC 的直角顶点 ,C ABC 的边上有两个动点 ,D E ，点 D 以1 /cm s 的 速度从点 A出发沿 AC CB 移动到点 B ，点 E 以3 /cm s 的速度从点 B 出发，沿 BC CA 移动到 点 A，两动点中有一个点到达终点后另一个点继续移动到终点过点 ,D E 分别作 ,DM PQ EN PQ ，垂足分别为点 ,M N .若 6 , 8AC cm BC cm  ，设运动时间为t ，则当 t  ___ s 时，以点 , ,D M C 为顶点的三角形与以点 , ,E N C 为顶点的三角形全等． 【答案】1 或 7 2 或12 【解析】分当 E 在 BC 线段上时，此时 D 在 AC 线段上；当 E 在 AC 线段上时，且 D 在 AC 线段上；当 E 到达 A 时，且 D 在 BC 线段上，三种情况进行讨论，相应列出方程求解即可. 【详解】解：当 E 在 BC 线段上时，此时 D 在 AC 线段上， 故 CE=8-3t，CD=6-t， 当 DC=CE 时， DCM CEN   故 8-3t =6-t 解得：t=1 当 E 在 AC 线段上时，且 D 在 AC 线段上， 故 CE=3t-8，CD=6-t， 当 DC=CE 时， DCM CEN   故 3t-8 =6-t 解得： 7 2t  当 E 到达 A 时，且 D 在 BC 线段上， 故 CE=6，CD=t-6， 当 DC=CE 时， DCM CEN   故 6 =t-6 解得： 12t  综上所述：t=1 或 7 2 或12时，，以点 , ,D M C 为顶点的三角形与以点 , ,E N C 为顶点的三角形全 等． 故答案为：1 或 7 2 或12 【点睛】本题考查了动点与三角形全等,分类讨论是解决本题的关键. 11．如图，已知以点 A(0，1)、C(1，0)为顶点的△ABC 中，∠BAC=60°，∠ACB=90°， 在坐标系内有一动点 P（不与 A 重合），以 P、B、C 为顶点的三角形和△ABC 全等，则 P 点 坐标为____________. 【答案】（2，-1）、(2 3, 3 1)  、( 3, 3 1) 【解析】 解：由勾股定理得：AC= 2 ，∵∠BAC=60°，∠ACB=90°，∴AB= 2 2 ，BC= 6 ，分为 三种情况： ①如图 1，延长 AC 到 P，使 AC=CP，连接 BP，过 P 作 PM⊥x 轴于 M，此时 PM=OA=1， CM=OC=1，OM=1+1=2，即 P 的坐标是（2，﹣1）； ②如图 2，过 B 作 BP⊥BC，且 BP=AC= 2 ，此时 PC=AB=2 2 ．过 P 作 PM⊥x 轴于 M， 此时∠PCM=15°，在 x 轴上取一点 N，使∠PNM=30°，即 CN=PN，设 PM=x，则 CN=PN=2x， MN= 3 x，在 Rt△CPM 中，由勾股定理得：（2 2 ）2=（2x+ 3 x）2+x2，x= 3 1 ，即 PM= 3 1 ， MC=2x+ 3 x= 3 1 ，OM=1+ 3 1 =2 3 ，即 P 的坐标是（ 2 3 ， 3 1 ）； ③如图 3，过 B 作 BP⊥BC，且 BP=AC= 2 ，过 P 作 PM⊥x 轴于 M，此时∠ PCM=30°+45°=75°，∠CPM=15°，和③解法类似求出 CM= 3 1 ， PM=2x+ 3 x= 3 1 ，OM=1+ 3 1 = 3 ，即 P 的坐标是（ 3 ， 3 1 ）． 故答案为：（2，﹣1）或（ 2 3 ， 3 1 ）或（ 3 ， 3 1 ）． 点睛：本题考查了全等三角形的性质和判定，勾股定理，含 30 度角的直角三角形等知识点的 应用，注意要进行分类讨论，题目比较好，但是有一定的难度． 12．如图，矩形 ABCD中， 4AB  ， 6AD  ，点 E 为 AD 中点，点 P 为线段 AB 上一个动点， 连接 EP ，将 APE 沿 PE 折叠得到 FPE ，连接CE ，CF ，当 ECF 为直角三角形时， AP 的 长为_____． 【答案】1 或 9 4 【解析】分两种情况进行讨论：当∠CFE=90°时，△ECF 是直角三角形；当∠CEF=90°时， △ECF 是直角三角形，分别根据直角三角形的勾股定理列方程求解即可． 【详解】分两种情况讨论： ①当∠CFE=90°时，△ECF 是直角三角形，如图 1 所示．由折叠可得：∠PFE=∠A=90°， AE=FE=DE，∴∠CFP=180°，即点 P，F，C 在一条直线上． 在 Rt△CDE 和 Rt△CFE 中， CE CE EF ED    ，∴Rt△CDE≌Rt△CFE（HL），∴CF=CD=4． 设 AP=FP=x，则 BP=4﹣x，CP=x+4． 在 Rt△BCP 中，BP2+BC2=PC2，即（4﹣x）2+62=（x+4）2，解得：x 9 4  ，即 AP 9 4  ； ②当∠CEF=90°时，△ECF 是直角三角形，如图 2 所示，过 F 作 FH⊥AB 于 H，作 FQ⊥AD 于 Q，则∠FQE=∠D=90°． 又∵∠FEQ+∠CED=90°=∠ECD+∠CED，∴∠FEQ=∠ECD，∴△FEQ∽△ECD，∴ FQ QE EF ED DC CE   ，即 3 3 4 5 FQ QE  ，解得：FQ 9 5  ，QE 12 5  ，∴AQ=HF 3 5  ，AH 9 5  ，设 AP=FP=x，则 HP 9 5   x． ∵Rt△PFH 中，HP2+HF2=PF2，即（ 9 5  x）2+（ 3 5 ）2=x2，解得：x=1，即 AP=1． 综上所述：AP 的长为 1 或 9 4 ． 【点睛】本题考查了折叠问题，矩形的性质，全等三角形的判定与性质，相似三角形的判定与 性质以及勾股定理．解题时注意：折叠前后两图形全等，即对应线段相等；对应角相等．本题 有两种情况，需要分类讨论，避免漏解． 13．如图， Rt ABC 中， 90 , 8, 3C AC BC     , , ,AE AC P Q 分别是 ,AC AE 上动点，且 PQ AB ，当 AP =_______时，才能使 ABC 和 PQA 全等. 【答案】3 或 8 【解析】 试题解析：分为两种情况：①当 AP=3 时， ∵BC=3， ∴AP=BC， ∵∠C=90°，AE⊥AC， ∴∠C=∠QAP=90°， ∴在 Rt△ABC 和 Rt△QAP 中， AB PQ BC AP    ＝ ＝ ∴Rt△ABC≌Rt△QAP（HL）， ②当 AP=8 时， ∵AC=8， ∴AP=AC， ∵∠C=90°，AE⊥AC， ∴∠C=∠QAP=90°， ∴在 Rt△ABC 和 Rt△QAP 中， AB PQ AC AP    ＝ ＝ ∴Rt△ABC≌Rt△QAP（HL）， 故答案为：3 或 8． 14．如图，已知 sinO＝ 3 3 ，OA＝6，点 P 是射线 ON 上一动点，当△AOP 为直角三角形时， 则 AP＝________． 【答案】3 2 或 2 3 【解析】分 AP⊥OA，AP⊥OP 两种情况讨论，当 AP⊥OA，可根据 sinO＝ 3 3 ，设 3 , 3AP x OP x= = ，利用勾股定理求出 x 即可求出 AP；当 AP⊥OP，直接利用 sinO＝ 3 3 和 AO=6，求得 AP. 【详解】当 AP⊥OA， ∵sinO＝ 3 3 ∴ 3 3 AP OP = 则设 3 , 3AP x OP x= = 在 Rt AOP 中根据勾股定理 2 2 2AP AO OP  即 2 23 36 9x x+ = 解得 1 6x  ， 2 6x   （舍去） ∴ 3AP x= =3 2 ； 当 AP⊥OP， ∵sinO＝ 3 3 ∴ 3 3 AP AO = ∴ 3 3 6 2 33 3AP AO= × = ´ = 故填3 2 或 2 3 . 【点睛】本题考查锐角三角函数，勾股定理.能利用分类讨论思想分情况讨论是解决此题的关 键. 15．如图，矩形 ABCD中 10AB  ， 12AD  ，点 E 是线段 BC 上一动点，连接 AE ，将 ABE 沿 直线 AE 折叠，点 B 落到 F 处，连接CF ，BF ，当 BFC 为等腰三角形时，BE 的长为__________． 【答案】10 3 或15 2 或 12 【解析】当 BFC 为等腰三角形时，有三种情况，需分别讨论：①：BF CF ；②：BF BC ； ③： BC CF . 【详解】①： BF CF ；首先，因为折叠， 10AB AF  ， BE FE ，则 EBF BFE∠ ∠ ，另 因 BF CF ，则 EBF BCF∠ ∠ ，可证得 BEF BFC  ，则 BE BF BF BC  ，因此只要求出 BF 的 值，即可求出 BE 的值，过点 F 朝 BC 作垂线，垂足为 I ，延长 FI 交边 AD 于点 H ，由矩形的 性质可知， 10AB HI  ， 12AD BC  ，利用等腰三角形三线合一的性质，可知 6BI CI AH   ，则在 Rt AHF 中， 2 2 8HF AF AH   ，则 2FI  ，再利用勾股定理，在 Rt BIF 中，有 2 2 2 10BF BI FI   ，由于 BEF BFC  ，则 BE BF BF BC  ， 2 12 40BF BE  ， 解得 10 3BE  . ②： BF BC ，若 AE 与 BF 交于点G ，首先因为折叠，可知 AE 为 BF 的垂直平分线，不难证 明出 AGB ABE  ，则 AG BG AB BE  ，则若能求得 AG 、 BG 的值，则此题便得以解答.因 12BC BF  ，则 6BG FG  ，在 Rt AGB 中， 2 2 8AG AB BG   ，则 8 6 10 BE  ，得 15 2BE  . ③：BC CF ，因 BC CF ，且因为折叠 AB AF ，则 AC 为线段 BF 的垂直平分线，所以点 E 与点C 重合， 12BE BC  . 故答案为10 3 或15 2 或 12. 【点睛】考查矩形的性质，翻折的性质，等腰三角形的性质，注意分类讨论思想在解题中的应 用. 16．如图，直线 1y x  与抛物线 2 4 5y x x   交于 A， B 两点，点 P 是 y 轴上的一个动点， 当 PAB 的周长最小时， PABS  _． 【答案】12 5 ． 【解析】根据轴对称，可以求得使得 PAB 的周长最小时点 P 的坐标，然后求出点 P 到直线 AB 的距离和 AB 的长度，即可求得 PAB 的面积，本题得以解决． 【详解】联立得 2 1 4 5 y x y x x       ， 解得， 1 2 x y    或 4 5 x y    ， ∴点 A的坐标为 1,2 ，点 B 的坐标为 4,5 ， ∴    2 25 2 4 1 3 2AB      ， 作点 A关于 y 轴的对称点 'A ，连接 'A B与 y 轴的交于 P ，则此时 PAB 的周长最小， 点 'A 的坐标为 1,2 ，点 B 的坐标为 4,5 ， 设直线 'A B的函数解析式为 y kx b  ， 2 4 5 k b k b       ，得 3 5 13 5 k b     ， ∴直线 'A B的函数解析式为 3 13 5 5y x  ， 当 0x  时， 13 5y  ， 即点 P 的坐标为 130, 5      ， 将 0x  代入直线 1y x  中，得 1y  ， ∵直线 1y x  与 y 轴的夹角是 45， ∴点 P 到直线 AB 的距离是： 13 8 2 4 21 sin 455 5 2 5          ， ∴ PAB 的面积是： 4 23 2 125 2 5   ， 故答案为12 5 ． 【点睛】本题考查二次函数的性质、一次函数的性质、轴对称﹣最短路径问题，解答本题的关 键是明确题意，利用数形结合的思想解答． 三、解答题 17．如图，抛物线 2 2 3y x mx m   与 x 轴交于 ,A B 两点，与 y 轴交于点  0, 3C  . （1）求该抛物线的解析式； （2）若点 E 为线段OC 上一动点，试求 2 2AE EC 的最小值； （3）点 D 是 y 轴左侧的抛物线上一动点，连接 AC ，当 DAB ACO∠ ∠ 时，求点 D 的坐标. 【答案】（1） 2 2 3y x x   ；（2） 2 2 22AE EC  ；（3）D 的坐标为 10 13,3 9     或 8 11,3 9      . 【解析】（1）把点  0,3C 代入抛物线表达式即可求出 m，即可得到抛物线的解析式；（2）连 接 BC ,过点 A作 AF BC 于点 F ，交 y 轴于点 E ，当 A E F、 、 三点共线时， 2 2AE EC 最 小值为 AF ，再根据由三角形面积公式得： 1 1• ·2 2BC AF AB OC ，即可求出 2 2AF  ；（3） 过 D 点作 x 轴的垂线，交 x 轴于点 H ，设点 D 的坐标为 2, 2 3m m m  ，利用 tan tanDAB ACO   即 BH AO AH CO  ，代入即可求出 m 的值，再求出 D 点坐标 【详解】解：（1）把点  0,3C 代入抛物线表达式得：9 6 3 0m m   ， 解得： 1m   故该抛物线的解析式为： 2 2 3y x x   （2）连接 BC ,过点 A作 AF BC 于点 F ，交 y 轴于点 E 由 2 2 3y x x   ，得：  3,0B  ，  0, 3C  OB OC  ,即 45ABC   ， 4, 3 2AB BC   由三角形面积公式得： 1 1• ·2 2BC AF AB OC 即： 1 13 2 4 32 2AF     ，解得： 2 2AF  在 Rt CEF 中， 2 2EF EC ， 2 2AE EC AE EF AF     当 A E F、 、 三点共线时， 2 2AE EC 最小值为 2 2AF  2 2 22AE EC   （3）过 D 点作 x 轴的垂线，交 x 轴于点 H ，设点 D 的坐标为 2, 2 3m m m  DAB ACO   tan tanDAB ACO    ，即 BH AO AH CO  2 2 3 1 1 3 m m m    或 2 2 3 1 1 3 m m m     解得： 10 3m   或 1（舍去 1m  ），或 1m  或 8 3  （舍去 1m  ） 过点 D 的坐标为 10 13,3 9     或 8 11,3 9      【点睛】此题主要考查二次函数综合，解题的关键是熟知三角函数的定义与性质及最值的求法. 18．如图,在菱形 ABCD中, DAB =60°, AB=2,点 E 是 AB 上的动点,作∠EDQ=60°交 BC 于 点 Q,点 P 在 AD 上,PD=PE. （1）求证：AE=BQ； （2）连接 PQ, EQ,当∠PEQ=90°时,求 DE PQ 的值； （3）当 AE 为何值时,△PEQ 是等腰三角形. 【答案】（1）见解析；（2） DE PQ = 3 2 ；（3）AE 为 4 2 3 或 2 【解析】（1）连结 DB，根据“ASA”证明△ADE≌△BDQ 即可； （2）先证明△DEQ 是等边三角形，可得∠DEQ=60°，进而可证明∠AED＝90°，根据勾股 定理求出 DE 的长，根据两平行线间的距离相等求出 PQ 的长，即可求出 DE PQ 的值； （3）分三种情况讨论求解：①当 QP=QE 时，②当 PE=QE 时，③当 PE=PQ 时. 【详解】解：（1）连结 DB, ∵四边形 ABCD 为菱形,∠A＝60°, ∴AD=AB＝DB,∠DBQ＝∠A＝60°. ∴∠ADB＝60°. ∵∠EDQ=60°, ∴∠ADE＝∠BDQ. ∴△ADE≌△BDQ. ∴AE=BQ. （2）如图， ∵△ADE≌△BDQ, ∴DE=DQ. ∵∠EDQ=60°， ∴△DEQ 是等边三角形， ∴∠DEQ=60°，DE=EQ=DQ. ∵∠PEQ=90°, ∴∠PED＝30°. ∵PD=PE, ∴∠PDE＝∠PED＝30°. ∴∠AED＝90°. ∵AD=2, ∴DE＝ 3 . ∵PD=PE, EQ=DQ, ∴PQ 是 DE 的中垂线, ∴PQ= AB=2. ∴ DE PQ = 3 2 . （3）①当 QP=QE 时,如图 1, ∵∠EQP＝∠DQP＝30°, ∴∠QPE＝∠QEP＝∠PDQ ＝75°. ∴∠PED＝∠PDE＝15°, ∴∠APE＝30°, ∴∠AEP＝90°. ∴AP＝2AE,PE＝PD＝ 3 AE, ∴ 3 AE＋2AE=2, ∴AE＝4 2 3 . ②当 PE=QE 时, ∵△DEQ 是正三角形， ∴△PDE 是正三角形,∠ADE＝60°, 点 E 与点 B 重合,如图 2, ∴AE=2. ③当 PE=PQ 时, ∵∠EQP＝30°, ∴∠PEQ=30°，由图可知∠PEQ≥60°, ∴点 E 不存在. 综上所述,当 AE 为 4 2 3 或 2 时,△PEQ 是等腰三角形. 【点睛】本题考查了菱形的性质，全等三角形的判定与性质，含 30°角的三角形的性质，等 边三角形的判定与性质，两平行线间的距离相等，等腰三角形的性质，以及分类讨论的数学思 想.掌握全等三角形的判定与性质是解（1）的关键，证明△DEQ 是等边三角形是解（2）的关 键，分类讨论是解（3）的关键. 19．已知：如图，∠B=90°AB∥DF，AB=3cm，BD=8cm，点 C 是线段 BD 上一动点，点 E 是直线 DF 上一动点，且始终保持 AC⊥CE． （1）试说明：∠ACB =∠CED （2）当 C 为 BD 的中点时，  ABC 与  EDC 全等吗？若全等，请说明理由；若不全等，请 改变 BD 的长（直接写出答案），使它们全等． （3）若 AC=CE ,试求 DE 的长 （4）在线段 BD 的延长线上，是否存在点 C，使得 AC=CE，若存在，请求出 DE 的长及△AEC 的面积；若不存在，请说明理由． 【答案】（1）见解析；（2）当 C 为 BD 中点时， ABC 与 EDC 不全等；（3）5cm；（4）见 解析. 【解析】（1）根据平行线的性质和三角形的内角和定理求出即可； （2）根据全等三角形的判定定理进行判断，即可得出答案； （3）根据全等得出对应边相等，即可得出答案； （4）求出两三角形全等，得出对应边相等，再根据勾股定理和三角形面积公式求出即可． 【详解】解：(1) 90 ,B AB DF   ， 90D B    ， ∵AC⊥CE， 90ACE  ， 90 , 90ECD CED ACB ECD         ， ACB CED   ； (2)当 C 为 BD 的中点时，△ABC 与△EDC 不全等，当 BD 的长是 6 时，它们全等， 理由是：∵BD=6，C 为 BD 中点， ∴BC=CD=3=AB， 在△ABC 和△CDE 中 90 ACB CED B D AB CD           ， (AAS)ABC CDE ≌ ； (3)∵在△ABC 和△CDE 中 ACB CED B D AC CE         ， (AAS)ABC CDE ≌ ， ∴AB=CD=3cm， ∴DE=BC=8cm−3cm=5cm； (4) 90B AB DF   ， ， 90CDE B    ， ∵AC⊥CE， 90ACE  ， 90 , 90ECD ACB ACB BAC         ， ∴∠ECD=∠BAC； 当 CD=AB=3cm 时，AC=CE， ∵在△ABC 和△CDE 中 B CDE AB CD BAC ECD         ， (ASA)ABC CDE ≌ ， ∴AC=CE，DE=BC=8cm， ∵AB=3cm，BC=BD+CD=8cm+3cm=11cm， ∴在 Rt ABC△ 中,由勾股定理得; 2 211 3 130AC    ， 90ACE   ， ∴△AEC 的面积是 21 1 130 130 65cm .2 2AC CE      【点睛】此题考查了全等三角形的判定与性质，勾股定理，三角形的面积的应用，熟练掌握全 等三角形的判定与性质是解本题的关键． 20．如图 1 所示，抛物线 2y ax bx c   交 x 轴于点  A 4,0 和点  B 1,0 ，交 y 轴于点  C 0,4 ．  1 求抛物线的函数表达式；  2 如图 2 所示，若点 M 是抛物线上一动点，且 AOM S BOCS 3 ，求点 M 的坐标；  3 如图 3 所示，设点 N 是线段 AC 上的一动点，作PN x 轴，交抛物线于点 P，求线段 PN 长度的最大值． 【答案】（1） 2y x 3x 4    ；（2）点 P 坐标为 3 37 ,32       或 3 37 ,32       或 3 13 , 32        或 3 13 , 32        ； 3 线段 PN 长度最大值为 4． 【解析】（1）把函数设为交点式，代入 C 点坐标，进而求出 a 的值即可； （2）设 M 点坐标为（x，-x2-3x+4），根据 S△AOM=3S △BOC 列出关于 x 的方程，解方程求出 x 的值，进而得到点 P 的坐标； （3）先运用待定系数法求出直线 AC 的解析式为 y=x+4，再设 N 点坐标为（x，x+4），则 P 点坐标为（x，-x2-3x+4），然后用含 x 的代数式表示 PN，根据二次函数的性质即可求出线段 PN 长度的最大值． 【详解】解：（1）把函数设为交点式   1 2y a x x x x   ， 由  A 4,0 ，  B 1,0 得   y a x 4 x 1   ，把  C 0,4 代入，得a 1  ， 故抛物线的解析式为 2y x 3x 4    ； （2）设 M 点坐标为 2x, x 3x 4   ， AOM S BOCS 3 ， 21 14 x 3x 4 3 1 42 2           ， 整理得 2x 3x 4 3   或 2x 3x 4 3    ， 解得 3 37x 2   或 3 13x 2   ， 则符合条件的点 P 坐标为 3 37 ,32       或 3 37 ,32       或 3 13 , 32        或 3 13 , 32        ； （3）设直线 AC 的解析式为 y kx b  ，将  A 4,0 ，  C 0,4 代入， 4k b 0 b 4      ， 解得 k 1 b 4    ， 即直线 AC 的解析式为 y x 4  ， 设点 N 坐标为 x,x 4 ， 4 x 0   ，则 P 点坐标为 2x, x 3x 4   ， 设 PN y ，则    2 2 2y x 3x 4 x 4 x 4x (x 2) 4             ， 即当 x 2  时，y 有最大值 4， 故线段 PN 长度最大值为 4． 【点睛】本题考查二次函数的综合问题，涉及待定系数法求函数解析式，面积问题以及线段最 值问题，熟练掌握二次函数的图像与性质是解题的关键. 21．如图，已知抛物线经过 A（1，0），B（0，3）两点，对称轴是 x=﹣1． （1）求抛物线对应的函数关系式； （2）动点 Q 从点 O 出发，以每秒 1 个单位长度的速度在线段 OA 上运动，同时动点 M 从 M 从 O 点出发以每秒 3 个单位长度的速度在线段 OB 上运动，过点 Q 作 x 轴的垂线交线段 AB 于点 N，交抛物线于点 P，设运动的时间为 t 秒． ①当 t 为何值时，四边形 OMPQ 为矩形； ②△AON 能否为等腰三角形？若能，求出 t 的值；若不能，请说明理由． 【答案】解：（1）根据题意，设抛物线的解析式为：  2y a x 1 k   ， ∵点 A（1，0），B（0，3）在抛物线上， ∴ 4a k 0{a k 3     ，解得： a 1{k 4    。 ∴抛物线的解析式为：  2y x 1 4    。 （2）①∵四边形 OMPQ 为矩形， ∴OM=PQ，即  23t t 1 4    ，整理得：t2+5t﹣3=0， 解得 5 37t 2   （ 5 37t 2   ＜0，舍去）。 ∴当 5 37t 2   秒时，四边形 OMPQ 为矩形。 ②Rt△AOB 中，OA=1，OB=3，∴tanA=3。 若△AON 为等腰三角形，有三种情况： （I）若 ON=AN，如答图 1 所示， 过点 N 作 ND⊥OA 于点 D， 则 D 为 OA 中点，OD= 1 2 OA= 1 2 ， ∴t= 1 2 。 （II）若 ON=OA，如答图 2 所示， 过点 N 作 ND⊥OA 于点 D， 设 AD=x，则 ND=AD•tanA=3x，OD=OA﹣AD=1﹣x， 在 Rt△NOD 中，由勾股定理得：OD2+ND2=ON2， 即   2 2 21 x 3x 1   ，解得 x1= 1 5 ，x2=0（舍去）。 ∴x= 1 5 ，OD=1﹣x= 4 5 。 ∴t= 4 5 。 （III）若 OA=AN，如答图 3 所示， 过点 N 作 ND⊥OA 于点 D， 设 AD=x，则 ND=AD•tanA=3x， 在 Rt△AND 中，由勾股定理得：ND2+AD2=AN2， 即  22 2x 3x 1  ，解得 x1= 10 10 ，x2= 10 10  （舍去）。 ∴x= 10 10 ，OD=1﹣x=1﹣ 10 10 。 ∴t=1﹣ 10 10 。 综上所述，当 t 为 1 2 秒、 4 5 秒，1﹣ 10 10 秒时，△AON 为等腰三角形。 【解析】 （1）用待定系数法求出抛物线的顶点式解析式。 （2）①当四边形 OMPQ 为矩形时，满足条件 OM=PQ，据此列一元二次方程求解。 ②△AON 为等腰三角形时，可能存在三种情形，分类讨论，逐一计算。 22．如图，在平面直角坐标系中，已知矩形 ABCD 的三个顶点 B（1，0），C（3，0），D（3， 4）．以 A 为顶点的抛物线 y=ax2+bx+c 过点 C．动点 P 从点 A 出发，沿线段 AB 向点 B 运动．同 时动点 Q 从点 C 出发，沿线段 CD 向点 D 运动．点 P，Q 的运动速度均为每秒 1 个单位．运 动时间为 t 秒．过点 P 作 PE⊥AB 交 AC 于点 E． （1）直接写出点 A 的坐标，并求出抛物线的解析式； （2）过点 E 作 EF⊥AD 于 F，交抛物线于点 G，当 t 为何值时，△ACG 的面积最大？最大值 为多少？ （3）在动点 P，Q 运动的过程中，当 t 为何值时，在矩形 ABCD 内（包括边界）存在点 H， 使以 C，Q，E，H 为顶点的四边形为菱形？请直接写出 t 的值． 【答案】解：（1）A（1，4）。 由题意，设抛物线解析式为 y=a（x﹣1）2+4 ∵抛物线过点 C（3，0），∴0=a（3﹣1）2+4，解得，a=﹣1。 ∴抛物线的解析式为 y=﹣（x﹣1）2+4，即 y=﹣x2+2x+3。 （2）设直线 AC 的解析式为 y=kx+b， ∵A（1，4），C（3，0）， ∴ 4 k b 0 3k b      ，解得 k 2 b 6     。 ∴直线 AC 的解析式为 y=﹣2x+6。 ∵点 P（1，4﹣t）， ∴将 y=4﹣t 代入 y=﹣2x+6 中，解得点 E 的横坐标为 tx 1 2   。 ∴点 G 的横坐标为 t1 2  ，代入抛物线的解析式中，可求点 G 的纵坐标为 2t4 4  。 ∴GE=（ 2t4 4  ）﹣（4﹣t）= 2tt 4  。 又点 A 到 GE 的距离为 t 2 ，C 到 GE 的距离为 t2 2  ， ∴   2 2 ACG AEG CEG 1 t 1 t t 1S S S EG EG 2 =EG=t = t 2 +12 2 2 2 4 4            （ ） 。 ∴当 t=2 时，S△ACG 的最大值为 1。 （3） 20t= 13 或 t=20 8 5 。 【解析】（1）根据矩形的性质可以写出点 A 得到坐标；由顶点 A 的坐标可设该抛物线的顶点 式方程为 y=a（x﹣1）2+4，然后将点 C 的坐标代入，即可求得系数 a 的值（利用待定系数法求抛物线 的解析式）。 （2）利用待定系数法求得直线 AC 的方程 y=﹣2x+6；由图形与坐标变换可以求得点 P 的坐 标 （1，4﹣t），据此可以求得点 E 的纵坐标，将其代入直线 AC 方程可以求得点 E 或点 G 的横 坐标；然后结合抛物线方程、图形与坐标变换可以求得 GE= 2tt 4  、点 A 到 GE 的距离为 t 2 ， C 到 GE 的 距 离 为 t2 2  ； 最 后 根 据 三 角 形 的 面 积 公 式 可 以 求 得  2 ACG AEG CEG 1S S S = t 2 +14      ，由二次函数的最值可以解得 t=2 时，S△ACG 的最大值为 1。 （3）因为菱形是邻边相等的平行四边形，所以点 H 在直线 EF 上。分 CE 是边和对角线两种情 况讨论即可。 由题设和（2）知，C（3，0），Q（3，t），E（ t1 ,4 t2   ），设 H（ t1 ,m2  ）。 当 CE 是对角线时，如图 1，有 CQ=HE=CH，即  2 2 22 2 22 4 t m=t m=4 2t 4 4 2t 3t 8t+16=0 13t 72t+80=0t 4m 3t 8t+16=02 +m =t2                   ， 解得， 20t= 13 或 t=4（舍去，此时 C，E 重合）。 当 CE 是边时，如图 2，有 CQ=CE=EH，即     22 22 m 4 t =t m=4 t 40t+80=0t t 40t+80=02 + 4 t =t2                 ， 解得， t=20 8 5 或 t=20+8 5 （舍去，此时已超过矩形 ABCD 的范围）。 综上所述，当 20t= 13 或 t=20 8 5 时，在矩形 ABCD 内（包括边界）存在点 H， 使以 C，Q，E，H 为顶点的四边形为菱形。 23．如图，平面直角坐标系 xOy 中点 A的坐标为  1,1 ，点 B 的坐标为 3,3 ，抛物线经过 A、 O、 E 三点，连接OA OB AB、 、 ，线段 AB 交 y 轴于点 E . （1）求点 E 的坐标； （2）求抛物线的函数解析式； （3）点 F 为线段OB 上的一个动点（不与点O、B 重合），直线 EF 与抛物线交于 M 、N 两点 （点 N 在 y 轴右侧），连接ON BN、 ，当四边形 ABNO的面积最大时，求点 N 的坐标并求出四 边形 ABNO面积的最大值. 【答案】（1） 3(0, )2 ；(2) 21 1 2 2y x x  ；(3) 最大值为 75 16 ，此时 N 点坐标为 3 3( , )2 8 【解析】 试题分析：（1）先利用待定系数法求出直线 AB 的解析式，然后计算自变量为 0 时的函数值即 可得到 E 点坐标； （2）利用待定系数求抛物线的解析式； （3）如图 1，作 / /NG y 轴交OB 于 G，如图，利用一次函数和二次函数图象上点的坐标特征， 设设 21 1( , )(0 3)2 2N m m m m   ，则  ,G m m ，再根据三角形面积公式计算出 AOBS 和 BONS ，然后得到 S 四边形 ABNO 和 m 的二次函数关系式，再根据二次函数的性质求解； 试题解析：（1）设直线 AB 的解析式为 y mx n  ， 把    1,1 , 3,3A B 代入得 1 3 3 m n m n       ，解得 1 2 3 2 m n     ， 所以直线 AB 的解析式为 1 3 2 2y x  ， 当 0x  时， 1 3 302 2 2y     ， 所以 E 点坐标为 3(0, )2 ； （2）设抛物线解析式为 2y ax bx c   ， 把      1,1 , 3,3 , 0,0A B O 代入得 1 9 3 3 0 a b c a b c c          ，解得 1 2 1 2 a b      ， 所以抛物线解析式为 21 1 2 2y x x  ； （3）如图 1，作 / /NG y 轴交OB 的解析式为 y x ， 设 21 1( , )(0 3)2 2N m m m m   ，则  ,G m m ， 2 21 1 1 3( )2 2 2 2GN m m m m m      ， 1 3 1 31 3 32 2 2 2AOB AOE BNGS S S           ， 2 21 1 3 3 93 ( )2 2 2 4 4BON ONG BNGS S S m m m m           所以 2 23 9 3 3 753 ( ) ,4 4 4 2 16BON AOBABNOS S S m m m          四边形 当 3 2m  时，四边形 ABNO面积的最大值，最大值为 75 16 ，此时 N 点坐标为 3 3( , )2 8 ； 24．如图 1,抛物线 2 1 1 2y ax x c   与 x 轴交于点 A和点  1,0B ,与 y 轴交于点 30, 4C      ,抛物线 1y 的顶点为 ,G GM x 轴于点 M ．将抛物线 1y 平移后得到顶点为 B 且对称轴为直l 的抛物线 2y ． (1)求抛物线 2y 的解析式； (2)如图 2,在直线l 上是否存在点T ,使 TAC 是等腰三角形?若存在,请求出所有点T 的坐标:若 不存在,请说明理由； (3)点 P 为抛物线 1y 上一动点,过点 P 作 y 轴的平行线交抛物线 2y 于点Q，点Q关于直线l 的对 称点为 R ，若以 , ,P Q R 为顶点的三角形与 AMC 全等,求直线 PR 的解析式． 【答案】（1）抛物线 2y 的解析式为 2 1 1 1 4 2 4y x x    ；（2）T 点的坐标为 1 3 137(1, )4T  , 2 3 137(1, )4T  , 3 77(1, )8T  ；（3） PR 的解析式为 1 3y x2 4    或 1 1 2 4y x   . 【解析】 分析：（1）把  1,0B 和 30, 4C      代入 2 1 1 2y ax x c   求出 a、c 的值，进而求出 y1，再根据平 移得出 y2 即可； （2）抛物线 2y 的对称轴l 为 1x  ,设  1,T t ,已知   33,0 , 0, 4A C      ，过点T 作TE y 轴于 E , 分三种情况时行讨论等腰三角形的底和腰，得到关于 t 的方程，解方程即可； （3）设 21 1 3, 4 2 4P m m m     ,则 21 1 1, 4 2 4Q m m m      ,根据对称性得 21 1 12 , 4 2 4R m m m       ,分点 P 在直线的左侧或右侧时,结合以 , ,P Q R 构成的三角形与 AMG 全等求解即可. 详解:(1)由题意知， 3 4 1 02 c a c       ， 解得 1 4a   ， 所以,抛物线 y 的解析式为 2 1 1 1 3 4 2 4y x x    ； 因为抛物线 1y 平移后得到抛物线 2y ,且顶点为  1,0B ， 所以抛物线 2y 的解析式为  2 2 1 14y x   ， 即： 2 2 1 1 1 4 2 4y x x    ； (2)抛物线 2y 的对称轴l 为 1x  ,设  1,T t ,已知   33,0 , 0, 4A C      ， 过点T 作TE y 轴于 E , 则 2 2 2 21TC TE CE    2 23 3 25 4 2 16t t t       ， 2 2 2TA TB AB    2 2 21 3 16t t    ， 2 153 16AC  ， 当TC AC 时， 即 2 3 25 153 2 16 16t t   ， 解得 1 3 137 4t  或 2 3 137 4t  ； 当TC AC 时,得 2 15316 16t   ，无解； 当TC AC 时,得 2 23 25 162 16t t t    ,解得 3 77 8t   ; 综上可知,在抛物线 2y 的对称轴l 上存在点T 使 TAC 是等腰三角形,此时T 点的坐标为 1 3 1371, 4T      , 2 3 1371, 4T      , 3 771, 8T     . (3)设 21 1 3, 4 2 4P m m m     ,则 21 1 1, 4 2 4Q m m m      , 因为 ,Q R 关于 1x  对称, 所以 21 1 12 , 4 2 4R m m m       , 情况一:当点 P 在直线的左侧时, 21 1 3 4 2 4PQ m m     21 1 1 14 2 4m m m        , 2 2QR m  , 又因为以 , ,P Q R 构成的三角形与 AMG 全等, 当 PQ GM 且QR AM 时, 0m  , 可求得 30, 4P     ,即点 P 与点C 重合 所以 12, 4R    , 设 PR 的解析式 y kx b  , 则有 3 ,4 12 .4 b k b       解得 1 2k   , 即 PR 的解析式为 1 3 2 4y x   , 当 PQ AM 且QR GM 时,无解, 情况二:当点 P 在直线l 右侧时, 21 1 1 4 2 4P Q m m      21 1 3 14 2 4m m m        , 2 2Q R m  , 同理可得 5 12, , 0,4 4P R             P R 的解析式为 1 1 2 4y x   , 综上所述, PR 的解析式为 1 3 2 4y x   或 1 1 2 4y x   . 点睛：本题主要考查了二次函数综合题，此题涉及到待定系数法求函数解析式、等腰三角形的 判定与性质、全等三角形的性质等知识，解答（1）问的关键是求出 a、c 的值，解答（2）、 （3）问的关键是正确地作出图形，进行分类讨论解答，此题有一定的难度． 25．如图．在平面直角坐标系中．抛物线 y＝ 1 2 x2+bx+c 与 x 轴交于 A 两点，与 y 轴交于点 C，点 A 的坐标为（﹣1，0），点 C 的坐标为（0，﹣2）．已知点 E（m，0）是线段 AB 上的 动点（点 E 不与点 A，B 重合）．过点 E 作 PE⊥x 轴交抛物线于点 P．交 BC 于点 F． （1）求该抛物线的表达式； （2）当线段 EF，PF 的长度比为 1：2 时，请求出 m 的值； （3）是否存在这样的 m，使得△BEP 与△ABC 相似？若存在，求出此时 m 的值；若不存在， 请说明理由． 【答案】（1） 21 3 22 2y x x   ；（2）m＝2 或 4；（3）存在，m 的值为 0 或 3． 【解析】（1）把点 A、点 C 的坐标代入抛物线表达式，即可求解； （2）设点 E 的坐标为（m，0），则点 F 的坐标为（m， 1 2 m﹣2），PE=2EF，即： 1 2 m﹣ 2 1 2  m2 3 2  m+2=2（2 1 2  m），即可求解； （3）当△BEP 与△ABC 相似，分∠EPB=∠CAB 或∠EPB=∠ABC 两种情况，求解即可． 【详解】抛物线过点 C，则其表达式为：y 1 2  x2+bx﹣2， 将点 A 坐标代入上式得：0 1 2   b﹣2， 解得：b 3 2   ， 故：抛物线的表达式为：y 1 2  x2 3 2  x﹣2； 设直线 BC 过点 C（0，﹣2），设其表达式为：y=kx﹣2， 将点 B 坐标代入上式得：0=4k﹣2， 解得：k 1 2  ，则直线 BC 的表达式为：y 1 2  x﹣2， 同理直线 AC 的表达式为：y=﹣2x﹣2， 设点 E 的坐标为（m，0），则点 F 的坐标为（m， 1 2 m﹣2）， 当线段 EF，PF 的长度比为 1：2 时，即：PE=2EF，则： 1 2 m﹣2 1 2  m2 3 2  m+2=2（2 1 2  m）， 解得：m=2 或 4； 直线 BC 的表达式为：y 1 2  x﹣2，直线 AC 的表达式为：y=﹣2x﹣2，则：BC⊥AC，当△BEP 与△ABC 相似，则∠EPB=∠CAB，或∠EPB=∠ABC， 即：tan∠EPB=tan∠CAB，或 tan∠EPB=tan∠ABC， 当 tan∠EPB=tan∠CAB 时，即： 2 4 21 3 22 2 m m m     ， 解得：m=0 或 4（舍去 m=4）， 同理，当 tan∠EPB=tan∠ABC，m=3 或 4（舍去 m=4）． 故存在，m 的值为 0 或 3． 【点睛】本题考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养．要会利用 数形结合的思想把代数和几何图形结合起来，利用点的坐标的意义表示线段的长度，从而求出 线段之间的关系． 26．如图，已知一次函数 1y 3 x b   的图像与 x 轴交于 A（-6,0）与 y 轴相交于点 B，动点 P 从 A 出发，沿 x 轴向 x 轴的正方向运动. （1）求 b 的值，并求出△PAB 为等腰三角形时点 P 的坐标； （2）在点 P 出发的同时，动点 Q 也从点 A 出发，以每秒 10 个单位的速度，沿射线 AB 运动， 运动时间为 t（s）； ①点 Q 的坐标（用含 t 的表达式表示）； ②若点 P 的运动速度为每秒 k 个单位，请直接写出当△APQ 为等腰三角形时 k 的值. 【答案】（1）解： 2b   ，当 PAB 为等腰三角形时点 P 的坐标为： 40 6,0 或 6,0 或 8 ,03    ；（2）①  3 6,Q t t  ，② k 的值分别为： 10 、6、 5 3 ． 【解析】（1）利用待定系数法把点 A 坐标代入一次函数解析式，即可求出 b 的值；若 PAB 为等腰三角形 ，需分 AP AB 、 PA PB 、 BP BA 三种情况分类讨论； （2）①设 Q 点横坐标为 a,因为 Q 点在射线 AB 上，所以横坐标为 1 23 a  ，即 1, 23Q a a     ， 作 QH x 轴于点 H ，则 1 23QH a  ， 6AH a  ，所以 110 23AQ a     ，又因为 10AQ t ，所以 1 23t a  ，解得 3 6a t  ，表示出  3 6,Q t t 坐标： ．②AP=tk,分 AP=AQ,AP=PQ,AQ=AP 三种情况即可解答, 【详解】（1）解：把 6x   ， 0y  代入 1 3y x b   得： 2b   ． ∴  0, 2B  ， 6AO  ， 2BO  ， 40AB  ． 当 AP AB 时， 40AP  ．∴  40 6,0P  ； 当 BP BA 时， 6OP OA  ．∴  6,0P ； 当 PA PB 时，设 OP x ，则 6PA PB x   ， 在 Rt OPB 中，由 2 2 2OP OB PB  可得： 8 3x  . ∴ 8 ,03P    ； 综上，当 PAB 为等腰三角形时点 P 的坐标为： 40 6,0 或 6,0 或 8 ,03    ． （2）①解：设 1, 23Q a a     ，作 QH x 轴于点 H ， 则 1 23QH a  ， 6AH a  ，∴ 110 23AQ a     ． 又∵ 10AQ t ，∴ 1 23t a  ，∴ 3 6a t  ， ∴  3 6,Q t t  ． ② k 的值分别为： 10 、6、 5 3 ． 【点睛】本题难度较大，考查一次函数及几何图形动点问题．动点为中考常考题型，需要学生 多做训练，培养数形结合思想，运用到考试中去． 27．如图，在平面直角坐标系中，已知矩形 OABC 的顶点 B（6，8），动点 M，N 同时从 O 点出发，点 M 沿射线 OA 方向以每秒 1 个单位的速度运动，点 N 沿线段 OB 方向以每秒 0.6 个单位的速度运动，当点 N 到达点 B 时，点 M，N 同时停止运动，连接 MN，设运动时间为 t（秒）． （1）求证△ONM～△OAB； （2）当点 M 是运动到点 25 ,03      时，若双曲线 ky x  的图象恰好过点 N，试求 k 的值； （3）△MNB 与△OAB 能否相似？若能试求出所有 t 的值，若不能请说明理由． 【答案】（1）见解析；（2）k＝12；（3）能，t＝6s 或 25 3 s 时，△BMN 与△AOB 相似． 【解析】（1）用含 t 的式子表示 OM，ON，可证得 ON OM OA OB  ，即可解决问题； （2）根据 M 点坐标可求得运动时间，进而求得 N 点坐标，再利用待定系数法求解析式即可 解决问题； （3）分两种情形解决）①当点 M 与点 A 重合时，△BNM∽△BAO，此时求得 t．②当 OM ＝BM 时，△MBN∽△BOA，此时点 M 在线段 OB 的垂直平分线上，可求得此时 t 值 【详解】 解：（1）证明：由题意：OA＝6，AB＝8，OB＝10，OM＝t，ON＝0.6t， ∴ ON OM OA OB  ， ∵∠MON＝∠AOB， ∴△ONM∽△OAB． （2）当 OM＝ 25 3 时，ON＝5， ∴ON＝NB， ∴N（3，4）， ∵双曲线 ky x  的图象恰好过点 N， ∴k＝12． （3）①当点 M 与点 A 重合时，△BNM∽△BAO，此时 t＝6s． ②当 OM＝BM 时，∠MBN＝∠AOB，∵∠OAB＝∠MNB＝90°， ∴△MBN∽△BOA， 此时点 M 在线段 OB 的垂直平分线上， 由（2）可知，此时 OM＝ 25 3 ，t＝ 25 3 s， 综上所述，当 t＝6s 或 25 3 s 时，△BMN 与△AOB 相似． 【点睛】本题考查反比例函数综合题、相似三角形的判定和性质、线段的垂直平分线的判定和 性质等知识，解题的关键是灵活运用所学知识解决问题，学会用分类讨论的思想思考问题，属 于中考压轴题． 28．如图，直线 AB 与 x 轴，y 轴分别交于点 A（2，0），点 B（0，2 3 ），动点 D 以 1 个单 位长度/秒的速度从点 A 出发向 x 轴负半轴运动，同时动点 E 以 3 个单位长度/秒的速度从点 B 出发向 y 轴负半轴运动，设运动时间为 t 秒，以点 A 为顶点的抛物线经过点 E，过点 E 作 x 轴的平行线，与抛物线的另一个交点为点 G，与 AB 相交于点 F （1）求∠OAB 度数； （2）当 t 为何值时，四边形 ADEF 为菱形，请求出此时二次函数解析式； （3）是否存在实数 t，使△AGF 为直角三角形？若存在，求 t 的值；若不存在，请说明理由． 【答案】（1）∠OAB＝60°；（2）t＝ 4 3 或 t＝4，四边形 ADEF 为菱形， 23 ( 2)2y x   ；（3） 存在，t＝ 4 3 ，使△AGF 为直角三角形，见解析. 【解析】（1）在 Rt△BOA 中，OA＝2，OB＝2 3 ，根据锐角三角函数的定义即可得出 tan ∠OAB 的值，进而得出∠OAB 的度数； （2）证明 DE∥AB，可得四边形 ADEF 为平行四边形，当 AD＝DE 时，四边形 ADEF 为菱形， 用 t 表示出 AD，DE 的长，解方程即可得出 t 的值，再设顶点式可求得此时二次函数的解析式； （3）由题意可得∠GFA＝∠BAO＝60°，∠FGA≠90°，所以使△AGF 为直角三角形，只 能是∠FAG＝90°，用 t 分别表示出 AF，FG 的长，根据 FG＝2AF，即可得出 t 的值． 【详解】解：（1）∵直线 AB 与 x 轴，y 轴分别交于点 A（2，0），点 B（0，2 3 ），∠BOA ＝90°， ∴OA＝2，OB＝2 3 ， ∴tan∠OAB＝ 3OB OA  ， ∴∠OAB＝60°； （2）∵AD＝t，BE＝ 3 tm ∴ 3BE OB DA OA   ， ∴DE∥AB， ∴∠EDO＝∠BAO＝60°， ∵过点 E 作 x 轴的平行线，与抛物线的另一个交点为点 G，与 AB 相交于点 F， ∴四边形 ADEF 为平行四边形， 当 AD＝DE 时，四边形 ADEF 为菱形， ∵OD＝2﹣t 或 OD＝t﹣2，DE＝2OD， ∴DE＝4﹣2t 或 DE＝2t﹣4， ∴t＝4﹣2t 或 t＝2t﹣4， 解得：t＝ 4 3 或 t＝4， 当 t＝ 4 3 时，点 E 坐标为（0， 2 3 3 ）， 设二次函数解析式为 y＝a（x﹣2）2， 将点 E 坐标代入，可得 a＝ 3 6 ， ∴二次函数解析式为 y＝ 3 6 （x﹣2）2； 当 t＝4 时，点 E 坐标为（0，-2 3 ）， 设二次函数解析式为 y＝a（x﹣2）2， 将点 E 坐标代入，可得 a＝ 3- 2 ， ∴二次函数解析式为 y＝ 3- 2 （x﹣2）2； （3）∵EG∥OA， ∴∠GFA＝∠BAO＝60°， ∵G 在二次函数图象上， ∴∠FGA≠90°， ∴使△AGF 为直角三角形，只能是∠FAG＝90°， 由对称性可得，EG＝4， ∵四边形 ADEF 为平行四边形， ∴EF＝AD＝t，AF＝DE＝2（2﹣t）， ∵FG＝2AF， ∴4﹣t＝4（2﹣t）， 解得：t＝ 4 3 ， ∴存在实数 t＝ 4 3 ，使△AGF 为直角三角形． 【点睛】本题考查用待定系数法求二次函数的表达式，锐角三角函数的定义，平行四边形、菱 形的判定，本题需注意分类讨论，不要漏解． 29．已知边长为 4 的正方形 ABCD，顶点 A 与坐标原点重合，一反比例函数图象过顶点 C， 动点 P 以每秒 1 个单位速度从点 A 出发沿 AB 方向运动，动点 Q 同时以每秒 4 个单位速度从 D 点出发沿正方形的边 DC→CB→BA 方向顺时针折线运动，当点 P 与点 Q 相遇时停止运动， 设点 P 的运动时间为 t． ⑴求出该反比例函数解析式； ⑵连接 PD，当以点 Q 和正方形的某两个顶点组成的三角形和△PAD 全等时，求 t 值； 【答案】（1）y=16 x ;（2）t= 4 5 或 t= 4 3 或 t= 8 5 . 【解析】 试题分析: （1）根据正方形 ABCD 的边长为 4，可得 C 的坐标为（4，4），再用待定系数法 求出反比例函数解析式； （2）分点 Q 在 CD，BC，AB 边上，根据全等三角形的判定和性质求得点 Q 的坐标； 试题解析: （1）∵正方形 ABCD 的边长为 4， ∴C 的坐标为（4，4） 设反比例解析式为 y= k x , 将 C 的坐标代入解析式得：k=16， ∴反比例解析式为 y=16 x . (2)当 Q 在 DC 上时，如图所示： 此时△APD≌△CQB， ∴AP=CQ,即 t=4−4t,解得 t= 4 5 ; 当 Q 在 BC 边上时，有两个位置，如图所示： 若 Q 在上边,则△QCD≌△PAD， ∴AP=QC,即 4t−4=t,解得 t= 4 3 ； 若 Q 在下边,则△APD≌△BQA， 则 AP=BQ,即 8−4t=t,解得 t= 8 5 ； 当 Q 在 AB 边上时，如图所示： 此时△APD≌△QBC， ∴AP=BQ,即 4t−8=t,解得 t= 8 3 ， 因为 0 ⩽ t ⩽ 125，所以舍去. 综上所述 t= 4 5 , t= 4 3 , t= 8 5 . 点睛: 本题考查了正方形的性质，待定系数法求反比例函数解析式，全等三角形的判定和性质， 三角形的面积计算，分类思想，综合性较强，有一定的难度． 30．综合与探究 如图 1，在平面直角坐标系中，抛物线 y＝ax2+ 8 3 x+3 与 x 轴交于 A，B 两点（A 在 B 左侧）， 与 y 轴交于点 C．点 A 坐标为（﹣1，0）．直线 l 为该抛物线的对称轴，且交直线 BC 于点 D．抛 物线上有一动点 P，且横坐标为 m（4＜m＜9），连接 PD，过点 P 作 PE⊥l 于点 E． （1）求抛物线及直线 BC 的函数表达式． （2）当△DEP 与△BOC 相似时，求 m 的值； （3）如图 2，点 M 为直线 BC 上一动点，是否存在点 P，使得以点 A，C，P．M 为顶点的四 边形是平行四边形？若存在，直接写出此时点 P 和点 M 的坐标；若不存在，说明理由． 【答案】（1）y＝－ 1 3 x+3，y＝﹣ 1 3 x2+ 8 3 x+3；（2）m 的值为 1 161 2   或 8；（3）存在点 P 坐标为（ 9 41 2  ， 29 41 6  ），点 M 坐标为（ 7 41 11 41,2 6   ） 【解析】（1）将点 A 坐标代入可求抛物线解析式，求出 B、C 坐标，待定系数法求出直线 BC 的解析式 （2）分类讨论相似关系，当△DEP～△COB 和当△DEP～ABOC 时，找好边角的对应关系， 可求 m 的值． （3）因为点 P 的坐标范围要求，所以点 P 只存在一种情况，利用全等关系，解方程等量关系 获得点 M 和 P 点坐标． 【详解】（1）把点 A（﹣1，0）代入 y＝ax2+ 8 3 x+3 中，得 a＝﹣ 1 3 ∴抛物线的函数表达式为， y＝﹣ 1 3 x2+ 8 3 x+3 当 x＝0，得 y＝3，∴点 C 的坐标为（0，3） 当 y＝0 时，得﹣y＝﹣ 1 3 x2+ 8 3 x+3＝0 解，得 x1＝﹣1，x2＝9．∵点 A 在点 B 左侧点 B 坐标为（9，0） 设直线 BC 的函数表达式为 y＝kx+b， 把点 B（9，0）和 C（0，3）代入上式， 得 9 0 •0 3 k b k b      解得 1 3 3 k b      ∴直线 BC 的函数表达式为 y＝－ 1 3 x+3； （2）在 Rt△BOC 中，OB＝9，OC＝3，∵PE⊥l 于点 E．∠PED＝∠BOC＝90°． ∵直线 l 为抛物线 y＝﹣ 1 3 x2+ 8 3 x+3 的对称轴， ∴直线 l 为 x＝﹣ 2 b a ＝﹣ 8 3 ÷[2×（﹣ 1 3 ）]＝4 ∴点 D 和 E 的横坐标为 4 把 x＝4 代入 y＝- 1 3 x+3 中，得 y＝- 1 3 x4+3＝ 5 3 ． ∴点 D 坐标为（4， 5 3 ） ∵点 P 是抛物线上的点， ∴设 P（m，﹣ 1 3 m2+ 8 3 m+3），E（4，﹣ 1 3 m2+ 8 3 m+3） ∵4＜m＜9，且△DEP 与△BOC 相似 ∴点 E 在点 D 上方，点 P 在点 E 右侧． ∴DE＝﹣ 1 3 m2+ 8 3 m+3﹣ 5 3 ＝﹣ 1 3 m2+ 8 3 m+ 4 3 ，PE＝m﹣4 ①当△DEP～ABOC 时， PE CO ＝ DE BO ， 即 4 3 m  ＝ 21 8 4 3 3 3 9 m m   解得 m1＝ 1 161 2   ，m2＝ 1 161 2   （舍） ②当△DEP～△COB 时， DE CO ＝ PE BO ， 即 21 8 4 3 3 3 3 m m   ＝ 4 9 m  解得 m1＝8，m2＝﹣1（舍） ∴当△DEP 与△BOC 相似时，m 的值为 1 161 2   或 8； （3）∵点 P 的横坐标在 4 与 9 之间 ∴A、C、P、M 组成的平行四边形只有一种情况，如图 可证△PMN≌△ACO（AAS） ∴OA＝MN＝1，PN＝CO＝3 设点 M（m，- 1 3 m+3） 则 P（m+1，- 1 3 m+3+3） 将点 P 坐标代入解析式，可解得 m＝ 7 41 2  ∴存在点 P 坐标为（ 9 41 2  ， 29 41 6  ），点 M 坐标为（ 7 41 11 41,2 6   ）. 【点睛】考查了待定系数法求解析式，相似存在性问题以及平行四边形存在性问题，综合内容 较多，是一道很好的入门级压轴问题． 31．如图，抛物线 与 轴交于 两点，与 轴交于点 ，其对称轴交抛物 线于点 ，交 轴于点 ，已知 . ⑴求抛物线的解析式及点 的坐标； ⑵连接 为抛物线上一动点，当 时，求点 的坐标； ⑶平行于 轴的直线交抛物线于 两点，以线段 为对角线作菱形 ，当点 在 轴 上，且 时，求菱形对角线 的长. 【答案】（1）y= x2﹣2x﹣6，D（2，﹣8）；（2）F 点的坐标为（7， ）或（5，﹣ ）；（3） 菱形对角线 MN 的长为 +1 或 ﹣1． 【解析】 试题分析：（1）由条件可求得 B、C 坐标，利用待定系数法可求得抛物线解析式，进一步可求 得 D 点坐标；（2）过 F 作 FG⊥x 轴于点 G，可设出 F 点坐标，利用△FAG∽△BDE，由相似 三角形的性质可得到关于 F 点坐标的方程，可求得 F 点的坐标；（3）可求得 P 点坐标，设 T 为菱形对角线的交点，设出 PT 的长为 n，从而可表示出 M 点的坐标，代入抛物线解析式可得 到 n 的方程，可求得 n 的值，从而可求得 MN 的长． 试题解析： （1）∵OB=OC=6， ∴B（6，0），C（0，﹣6）， ∴ ，解得 ， ∴抛物线解析式为 y= x2﹣2x﹣6， ∵y= x2﹣2x﹣6= （x﹣2）2﹣8， ∴点 D 的坐标为（2，﹣8）； （2）如图 1，过 F 作 FG⊥x 轴于点 G， 设 F（x， x2﹣2x﹣6），则 FG=| x2﹣2x﹣6|， 在 y= x2﹣2x﹣6 中，令 y=0 可得 x2﹣2x﹣6=0，解得 x=﹣2 或 x=6， ∴A（﹣2，0）， ∴OA=2，则 AG=x+2， ∵B（6，0），D（2，﹣8）， ∴BE=6﹣2=4，DE=8， 当∠FAB=∠EDB 时，且∠FGA=∠BED， ∴△FAG∽△BDE， ∴ ，即 = ， 当点 F 在 x 轴上方时，则有 ，解得 x=﹣2（舍去）或 x=7，此进 F 点坐标为（7， ）； 当点 F 在 x 轴上方时，则有 ，得 x=﹣2（舍去）或 x=5，此进 F 点坐标为（5， ﹣ ）； 综上可知 F 点的坐标为（7， ）或（5，﹣ ）； （3）∵点 P 在 x 轴上， ∴由菱形的对称性可知 P（2，0）， 如图 2，当 MN 在 x 轴上方时，设 T 为菱形对角线的交点， ∵PQ= MN， ∴MT=2PT， 设 PT=n，则 MT=2n， ∴M（2+2n，n）， ∵M 在抛物线上， ∴n= （2+2n）2﹣2（2+2n）﹣6，解得 n= 或 n= ， ∴MN=2MT=4n= +1； 当 MN 在 x 轴下方时，同理可设 PT=n，则 M（2+2n，﹣n）， ∴﹣n= （2+2n）2﹣2（2+2n）﹣6，解得 n= 或 n= （舍去）， ∴MN=2MT=4n= ﹣1； 综上可知菱形对角线 MN 的长为 +1 或 ﹣1． 考点：二次函数综合题． 32．如图，已知直线 4 43y x   与抛物线 2 8 3y ax x b   交于点 A、C 两点，抛物线与 x 轴另 一交点为 B . （1）求抛物线的解析式； （2）若点 P 为直线 AC 上一动点，点 P 从点 A出发，沿 AC 以每秒 1 个单位长度的速度向点C 作匀速运动，设运动时间为  0t s t  .当 PAO 与 ABC 相似时，求出点 P 的运动时间t ； （3）点 M 是位于直线 AC 上方 y 轴上一点，点 N 为直线 AC 上一点，点Q 为第一象限内抛物 线上一动点，是否存在以点C ， M ， N ，Q 为顶点的四边形是菱形？若存在，直接写出点 N 的坐标；若不存在，请说明理由. 【答案】（1） 24 8 43 3y x x    ；（2）当 PAO 与 ABC 相似时， 12 5t s 或15 4 s ；（3）存在， 点 N 的坐标为 161, 3     或 7 5,4 3     . 【解析】（1）先求出  3,0A ，  0,4C ，代入二次函数解析式，即可求解； （2）根据二次函数解析式求出  1,0B  ，求出 AC，AB，设 PA t ，分两种情况讨论： ①当 1PAO BAC  时，②当 2P AO CAB  时，分别列出比例式进行求解； （3）设  24 8, 4 0 33 3Q m m m m        ，①当CM 为对角线时，四边形CQMN 为菱形，利用 点 N 和点Q 关于 y 轴对称，得到 24 8, 43 3N m m m       ，代入 4 43y x   中求出 m,②当CM 为菱形的边时，四边形CNQM 为菱形，根据 NQ CN ，设 4, 43N m m    ，表示出 NQ ， CN ， 再列出方程即可求出 m. 【详解】（1）∵直线 4 43y x   ，当 0y  时，即 4 4 03 x   ，解得 3x  ， 当 0x  时， 4y  ， ∴  3,0A ，  0,4C ， ∴ 9 8 0 4 a b b      ，∴ 4 3 4 a b      . ∴抛物线的解析式为 24 8 43 3y x x    ； （2）∵抛物线解析式为 24 8 43 3y x x    ， ∴  1,0B  ， ∴ 2 23 4 5AC    ， 4AB  ，设 PA t ， ∵ PAO BAC   ，∴需分两种情况讨论： 如解图①，①当 1PAO BAC  时， ∴ 1P A AO BA AC  ， 即 3 4 5 t  ， ∴ 12 5t  ， ②当 2P AO CAB  时， ∴ 2P A OA CA AB  ， 即 3 5 4 t  ，∴ 15 4t  ， 综上所述，当 PAO 与 ABC 相似时， 12 5t s 或15 4 s ； （3）存在点 N 的坐标为 161, 3     或 7 5,4 3     .理由如下： 设  24 8, 4 0 33 3Q m m m m        ， 当CM 为对角线时，四边形CQMN 为菱形，如解图②，则点 N 和点Q 关于 y 轴对称，∴ 24 8, 43 3N m m m       ， 把 24 8, 43 3N m m m       代入 4 43y x   中，得 24 4 84 43 3 3m m m     ，解得 1 0m  （舍去）， 2 1m  ，此时点 N 的坐标为 161, 3     ；当CM 为菱形的边时，四边形CNQM 为菱形，如解图③， 则 / /NQ y 轴， NQ CN ，设 4, 43N m m    ，∴ 24 8 44 43 3 3NQ m m m         24 43 m m   ， 2 2 2 24 254 43 9CN m m m         ，即 5 3CN m ，∴ 24 543 3m m m   ，解得 1 0m  （舍去）， 2 7 4m  ，此时 N 点坐标为 7 5,4 3     ， 综上所述，存在以点C 、M 、N 、Q 为顶点的四边形是菱形，满足条件的点 N 的坐标为 161, 3     或 7 5,4 3     . 【点睛】此题主要考查二次函数综合，解题的关键是熟知待定系数法、二次函数的图像、菱形 的性质及相似三角形的判定与性质. 33．如图 1，在平面直角坐标系中，抛物线 y＝﹣x2+bx+c 与 x 轴分别交于 A（﹣3，0），B 两点，与 y 轴交于点 C，点 D 为抛物线的顶点，抛物线的对称轴是 x＝﹣1，且与 x 轴交于 E 点． （1）请直接写出抛物线的解析式及顶点 D 的坐标； （2）如图 2，连接 AD，设点 P 是线段 AD 上的一个动点，过点 P 作 x 轴的垂线交抛物线于 点 G，交 x 轴于点 H，连接 AG、GD，当△ADG 的面积为 1 时， ①求点 P 的坐标； ②连接 PC、PE，探究 PC、PE 的数量关系和位置关系，并说明理由; （3）设 M 为抛物线上一动点，N 为抛物线的对称轴上一动点，Q 为 x 轴上一动点，当以 Q、 M、N、E 为顶点的四边形为正方形时，请直接写出点 Q 的坐标． 【答案】（1）y＝﹣x2﹣2x+3，顶点 D 坐标为（﹣1，4）；（2）①P（﹣2，2）；②PC＝PE， PC⊥PE，理由见解析；（3）Q（ 3 17 2   ，0）或（ 3 17 2   ，0）或（ 1 17 2   ，0）或（ 1 17 2   ， 0） 【解析】（1）根据待定系数法，即可得到答案； （2）①易求：直线 AD 的解析式为：y＝2x+6，设点 P（m，2m+6）（﹣3＜m＜﹣1），则 G （m，﹣m2﹣2m+3），得到 PG=﹣m2﹣4m﹣3，结合 S△ADG＝1，列出关于 m 的方程即可； ②连接 CE，根据勾股定理分别求出 PC，PE， CE 的值，即可得到 PC、PE 的数量关系和位 置关系； （3）设 N（﹣1，n），Q（p，0），根据题意得：M（p，n），|p+1|＝|n|，﹣p2﹣2p+3 ＝n，即可求出点 Q 的坐标. 【详解】（1）∵抛物线 y＝﹣x2+bx+c 的对称轴是 x＝﹣1， ∴﹣ 2 ( 1) b   ＝﹣1， ∴b＝﹣2， ∴抛物线 y＝﹣x2+bx+c 的解析式为 y＝﹣x2﹣2x+c， ∵抛物线过点 A（﹣3，0）， ∴0＝﹣9+6+c， ∴c＝3， ∴抛物线的解析式为 y＝﹣x2﹣2x+3， ∴顶点 D 坐标为（﹣1，4）； （2）①由（1）知，D（﹣1，4）， ∵A（﹣3，0）， ∴直线 AD 的解析式为：y＝2x+6， 设点 P（m，2m+6）（﹣3＜m＜﹣1）， 由（1）知，抛物线的解析式为：y＝﹣x2﹣2x+3， ∵PH⊥x 轴， ∴G（m，﹣m2﹣2m+3）， ∴PG＝﹣m2﹣2m+3﹣（2m+6）＝﹣m2﹣4m﹣3， ∵△ADG 的面积为 1， ∴S△ADG＝ 1 2 PG×（﹣1+3）＝﹣m2﹣4m﹣3＝1， ∴m＝﹣2， ∴P（﹣2，2）； ②如图 2，连接 CE，由（1）知，抛物线的解析式为 y＝﹣x2﹣2x+3， ∴C（0，3）， 由①知，P（﹣2，2）， ∵抛物线的对称轴 x＝1， ∴E（﹣1，0）， ∴PC＝ 2 22 (2 3) 5   ，PE＝ 2 2( 2 1) 2   ＝ 5 ， CE＝ 2 21 3 10  ， ∴PC＝PE，PC2+PE2＝5+5＝10＝CE2， ∴△PCE 是以 CE 为斜边的直角三角形， ∴∠CPE＝90°． ∴PC⊥PE； （3）设 N（﹣1，n），Q（p，0）， ∵以 Q、M、N、E 为顶点的四边形为正方形， ∴M（p，n），|p+1|＝|n|①， ∵点 M 在抛物线上， ∴﹣p2﹣2p+3＝n②， 联立①②解得， 3 17 2 1 17 2 p n       或 3 17 2 1 17 2 p n       或 1 17 2 3 17 2 p n       或 1 17 2 3 17 2 p n       ， ∴Q（ 3 17 2   ，0）或（ 3 17 2   ，0）或（ 1 17 2   ，0）或（ 1 17 2   ，0）． 【点睛】本题主要考查二次函数与平面几何的综合，根据题意，画出草图，是解题的关键，体 现了数形结合的思想方法. 34．已知二次函数 2 2 ( 0)y ax ax c a    的图象与 x 轴的负半轴和正半轴分别交于 A、B 两点， 与 y 轴交于点 C，它的顶点为 P，直线CP 与过点 B 且垂直于 x 轴的直线交于点 D，且 : 1: 2CP PD  （1）求 A、B 两点的坐标； （2）若 tan 1PDB  ，求这个二次函数的关系式； （3）在（2）的基础上，将直线CP 先绕点 C 旋转到与 x 轴平行，再沿 y 轴向上平移 1 个单 位得直线 n，Q 是直线 n 上的动点，是否存在点 Q，使 OPQ 为直角三角形？若存在，求出 所有点 Q 的坐标；若不存在，请说明理由． 【答案】（1）A（-1，0），B（3，0）；（2） 2 2 3y x x   ；（3）点 Q 的坐标为 1 17 , 22        或 1 17 , 22        或（9，-2）或（-8，-2）. 【解析】（1）先求出抛物线的对称轴，然后利用平行线分线段成比例定理求得 OE：EB 的值， 从而得到点 B 的坐标，利用抛物线的对称性可求得点 A 的坐标； （2）过点 C 作 CF⊥PE，垂足为 F，用字母表示出点 C 和点 P 的坐标，然后根 EF∥BD，则 ∠FPC=∠PDB，然后利用锐角三角函数的定义可求得 a 的值，然后将点 A 坐标代入抛物线的 解析式可求得 c 的值； （3）先求得抛物线的顶点坐标，然后再求得直线 n=-2．设点 Q 的坐标为（a，-2），依据两 点间的距离公式可知： 2 17PO  ， 2 21 4PQ a  （ ） ， 2 2 4OQ a  ，然后分三种情况依据勾股 定理的逆定理列方程分别求出 Q 点坐标即可. 【详解】解：（1）按照题意画出二次图像，如图所示： 作 PE⊥x 轴， ∵由题意可知：抛物线的对称轴为 2 12 2 b ax a a      ， ∴OE=1， ∵OC∥PE∥BD， ∴ 1 2 EO CP BE CD   ， ∴BE=2， ∴OB=3， ∴B（3，0）， ∵点 A 与点 B 关于 PE 对称， ∴点 A 的坐标为（-1，0）； （2）过点 C 作 CF⊥PE，垂足为 F， 将 x=0 代入得：y=c， ∴点 C 的坐标为（0，c）， 将 x=1 代入得 y=-a+c， ∴点 P 的坐标为（1，-a+c）， ∴PF=a， ∵PE∥BD，tan∠PDB=1， ∴tan∠FPC=1， ∴ 1 1CF PF a   ，解得 a=1， 将 a=1 代入抛物线的解析式得： 2 2y x x c   ， 将点 A 的坐标代入得：1+2+c=0，解得：c=-3， ∴抛物线的解析式为 2 2 3y x x   ； （3）∵  22 2 3 1 4y x x x      ， ∴点 P 的坐标为（1，-4）， 由题意可知：直线 n=-2， 设点 Q 的坐标为（a，-2），依据两点间的距离公式可知： 2 17PO  ， 2 21 4PQ a  （ ） ， 2 2 4OQ a  ， ①当 2 2 2PQ OQ PO  时， 2 21 4 4 17a a     ，解得： 1 17 2a   或 1 17 2a   ， ∴点 Q 的坐标为 1 17 , 22        或 1 17 , 22        ， ②当 2 2 2PO PQ OQ  时，  2 217 1 4 4a a     ，解得 a=9， ∴点 Q 的坐标为（9，-2）； ③当 2 2 2PO OQ PQ  时，  2217 4 1 4a a     ，解得：a=-8， ∴点 Q 的坐标为（-8，-2）， 综上所述，点 Q 的坐标为 1 17 , 22        或 1 17 , 22        或（9，-2）或（-8，-2）. 【点睛】本题主要考查的是二次函数的综合应用，解答本题主要应用了抛物线的对称性，锐角 三角函数的定义，平行线分线段成比例定理，勾股定理的逆定理.其中作CF 垂直于对称轴，利 用锐角三角函数的定义求得 a 的值是解题的关键．注意（3）要分情况讨论. 35．如图，在平面直角坐标系中，直线 l1：y＝﹣ 1 2 x+2 向下平移 1 个单位后，得到直线 l2，l2 交 x 轴于点 A，点 P 是直线 l1 上一动点，过点 P 作 PQ∥y 轴交 l2 于点 Q （1）求出点 A 的坐标； （2）连接 AP，当△APQ 为以 PQ 为底边的等腰三角形时，求点 P 和点 Q 的坐标； （3）点 B 为 OA 的中点，连接 OQ、BQ，若点 P 在 y 轴的左侧，M 为直线 y＝﹣1 上一动点， 当△PQM 与△BOQ 全等时，求点 M 的坐标． 【答案】（1）A(2，0)；（2）P(3， 1 2 )，Q(3，﹣ 1 2 )；（3）M(﹣1，﹣1)或(﹣1，8) 【解析】（1）求出直线 l2 的解析式为 y＝﹣ 1 2 x+1，即可求 A 的坐标； （2）设点 P（x，﹣ 1 2 x+2），Q（x，﹣ 1 2 x+1），由 AQ＝AP，即可求 P 点坐标； （3）设 P（n，﹣ 1 2 n+2），M（m，﹣1），则 Q（n，﹣ 1 2 n+1），可求出 BQ＝ 2 2 1(1 ) 12n n       ， OQ＝ 2 2 1 12n n      ，PM＝ 2 2 1( ) 2 12n n         ，QM＝ 2 2 1( ) 1 12n n         ， ①当△PQM≌△BOQ 时，PM＝BQ，QM＝OQ，结合勾股定理，求出 m；②当△QPM≌△ BOQ 时，有 PM＝OQ，QM＝BQ，结合勾股定理，求出 m 即可． 【详解】解：（1）∵直线 l1：y＝﹣ 1 2 x+2 向下平移 1 个单位后，得到直线 l2， ∴直线 l2 的解析式为 y＝﹣ 1 2 x+1， ∵l2 交 x 轴于点 A， ∴A（2，0）； （2）当△APQ 为以 PQ 为底边的等腰三角形时， ∴AQ＝AP， ∵点 P 是直线 l1 上一动点， 设点 P（x，﹣ 1 2 x+2）， ∵过点 P 作 PQ∥y 轴交 l2 于点 Q ∴Q（x，﹣ 1 2 x+1）， ∴（﹣ 1 2 x+2）2＝（﹣ 1 2 x+1）2， ∴x＝3， ∴P（3， 1 2 ），Q（3，﹣ 1 2 ）； （3）∵点 B 为 OA 的中点， ∴B（1，0）， ∴PQ＝BO＝1， 设 P（n，﹣ 1 2 n+2），M（m，﹣1），则 Q（n，﹣ 1 2 n+1）， ∴BQ＝ 2 2 1(1 ) 12n n       ，OQ＝ 2 2 1 12n n      ， PM＝ 2 2 1( ) 2 12n n         ，QM＝ 2 2 1( ) 1 12n n         ，① ∵△PQM 与△BOQ 全等， ①当△PQM≌△BOQ 时， 有 PM＝BQ，QM＝OQ， 2 2 2 1( 1) 2n mn         ＝ 2 2 1(1 ) 12n n       ， 2 2 1 1( 1) 2nn m       ＝ 2 2 1 12n n      ， ∴n＝2m﹣2， ∵点 P 在 y 轴的左侧， ∴n＜0， ∴m＜1， ∴m＝﹣1， ∴M（﹣1，﹣1）； ②当△QPM≌△BOQ 时， 有 PM＝OQ，QM＝BQ， 2 2 2 1( 1) 2n mn         ＝ 2 2 1 12n n      ， 2 2 1 1( 1) 2nn m       ＝ 2 2 1(1 ) 12n n       ， ∴n＝ 4 3 ﹣ 2 3 m， ∵点 P 在 y 轴的左侧， ∴n＜0， ∴m＞2， ∴m＝8， ∴M（﹣1，8）； 综上所述，M（﹣1，﹣1）或 M（﹣1，8）．1：y＝﹣ 1 2 x+2 向下平移 1 个单位后，得到直线 l2， 【点睛】本题考查一次函数的综合；熟练掌握一次函数的图象特点，等腰三角形与全等三角形 的性质是解题的关键． 36．如图，在平面直角坐标系中，直线 3 4 3y x  分别交 x 轴、 y 轴于点 A、C ，直线 BC 与直线 AC 关于 y 轴对称，动点 D 从点 A出发，沿 AC 以每秒 2 个单位长度的速度向终点C 运 动.当点 D 出发后，过点 D 作 DE BC‖ 交折线 A O C  于点 E ，以 DE 为边向上作等边 DEF ， 设 DEF 与 ACO 重叠部分图形的面积为 S .点 D 运动的时间为t 秒. （1）写出坐标：点 A（ ）， B （ ），C （ ）； （2）当点 E 在线段 AO 上时，求 S 与t 之间的函数关系式； （3）求出以点 B 、 E 、 F 为顶点的三角形是直角三角形时t 的值； （4）直接写出点 F 运动的路径长为 . 【答案】（1）( 4,0) ，(4,0) ， 3 4 5 1a a a  ；（2）①当 40 3t ＜ 时， 23S t ，②当 4 23 t ＜ 时， 27 3 12 3 8 32S t t    ；（3）t 的值是 4 3 秒或 8 3 秒；（4） 4 3 4 . 【解析】(1)分别令 0x  和 0y  代入直线 3 4 3y x  中，可得 A 和C 的坐标，根据对称 性可得出 B 的坐标 (2)根据三角函数特殊值求 60CAO   ,得 ADE 是等边三角形，表示 2AD AE t  ，计算当 点 F 在OC 上时，如图 1，根据 2 4AO AE OE t t     ，列出方程可得t 的值 ①当 40 3t  时，点 E 在线段OA 上， DEF 与 ACO 重叠部分图形是等边三角形 DEF , 如图 2 ②当 4 23 t  时，如图 3， DEF 与 ACO 重叠部分图形是四边形 DEGH ,根据面积差可得结 论； (3) ①如图 4，当0 2t  时， 90EFB   ,根据 2 2BE EF AD  列出可得结论； ②如图 5，当 2 4t  时， E 在 y 轴上，根据 2BF AD t  ，得t 的值 (4) ①点 E 在线段OA 上时，如图 6，点 F 的运动路径为等边 ACB 中 BC 边上的高线 AF ， ②点 E 在线段OC 上时，设 BC 的中点为 P ，如图 7，点 F 的运动路径为 PC 的长，相加即可 得出答案. 【详解】解：（1） 0x  时， 4 3y  ，  0,4 3C ， 当 0y  时， 3 4 3 0x   ， 4x   ，  4,0A  ， 直线 BC 与直线 AC 关于 y 轴对称，  4,0B . （2） Rt ACO 中， 4 3 34 COtan CAO AO     ， 60CAO   , AC BC  , 60ABC CAO     , DE BC , 60AED ABC     , ADE 是等边三角形， 2AD AE t   ， 当点 F 在OC 上时，如图①， 60AED DEF     ， 60OEF   ， 90EOF   ， 2EF DE AD t    ， 1 2OE EF t   ， 2 4AO AE OE t t      4 3t  . ① 当 40 3t ＜ 时，点 E 在线段OA 上， DEF 与 ACO 重叠部分图形是等边三角形 DEF , 如图 2  2 23 2 34S t t  . ② 当 4 23 t＜  时， 如图 3， DEF 与 ACO 重叠部分图形是四边形 DEGH 2AE t ， 4 2OE t  ， Rt EOG 中， 30EGO   ，  3 3 4 2OG OE t    ，  3 3 4 2 3 3 4 3GH OH OG t t t        . Rt FHG 中， 30HGF   ， 3 4 3 GHFH t    ，   2 21 7 33 3 3 4 3 3 4 12 3 8 32 2DEF GHFS S S t t t t t            （3）①如图 4， 当0 2t ＜ 时， 90EFB   ， 30FBE   ， 2 2BE EF AD   ， 则8 2 4t t  ， 4 3t  . ② 如图 5， 当 2 4t＜ ＜ 时， E 在 y 轴上， 90FEB   ， 30FBE   ， 60ABC   ， 30EBO   ， 4OB  ， 4 3 3OE  ， 8 3 3BE  ， 8 3EF  ， 16 3BF  ， BF AD ， 162 3t  ， 8 3t  ， 综上，t 的值是 4 3 秒或 8 3 秒. （4）动点 D 从点 A出发， DE BC ，点 E 在线段OA上时，如图 6， 点 F 的运动路径为等边 ACB 中 BC 边上的高线 AF ， 此时 2 28 4 4 3AF    ， 当点 E 在线段OC 上时，设 BC 的中点为 P ，如图 7， 点 F 的运动路径为 PC 的长， 1 42PC BC  ,点 F 运动的路径长为： 4 3 4 . 【点睛】本题主要考查了一次函数与 x 轴，y 轴的交点的求法，三角函数的定义，勾股定理及 几何动点问题，此类题型常用方程的思想解决问题，分类讨论思想是解题关键. 37．如图，在矩形OABC 中，点O为原点，点 A的坐标为 0,4 3 ，点C 的坐标为 4,0 ，抛物 线 23 2y x bx c    经过点 A、C ，与 AB 交于点 D ． 备用图 ⑴求抛物线的函数解析式； ⑵点 P 为线段 BC 上一个动点（不与点C 重合），点Q 为线段 AC 上一个动点， 2 3 3AQ CP ， 连接 PQ ，设CP m ， CPQ 的面积为 S ．求 S 关于 m 的函数表达式； ⑶抛物线 23 2y x bx c    的顶点为 F ，对称轴为直线l ，当 S 最大时，在直线l 上，是否存 在点 M ，使以 M 、Q 、 D 、F 为顶点的四边形是平行四边形，若存在，请写出符合条件的点 M 的坐标；若不存在，请说明理由． 【答案】（1） 23 3 4 32y x x    ；（2） 23 26   S m m ；（3）点 M 的坐标为 13 31, 2       ， 5 31, 2       【解析】（1）直接利用待定系数法，即可求出解析式； （2）根据特殊角的三角函数值，得到 30ACB OAC     ，过点Q 作QE BC 与 E 点，则 1 2QE CQ ，然后根据面积公式，即可得到答案； （3）由（2）可知，当 2 3m  时， S 取最大值，得到点 Q 的坐标，然后求出点 D 和点 F 的 坐标，再根据平行四边形的性质，有 MF DQ ，然后列出等式，即可求出点 M 的坐标. 【详解】解：（1） 2y x bx c    经过 A、C 两点 4 3 8 3 4 0 c b c       ，解得 4 3 3 c b    ， ∴抛物线的解析式为： 23 3 4 32y x x    ； （2） 4 3OA  ， 4OC  ，  22 2 24 3 4 8AC OA OC      ， ∴ 4 1sin 8 2OAC   ， 30ACB OAC    ， 过点Q 作QE BC 于 E 点，则 ∴ 1 1 2 382 2 3QE CQ m        ， 21 1 1 2 3 38 22 2 2 3 6S CP QE m m m m              ； （3）存在符合条件的点 M ，理由如下： 由⑵得，  223 32 2 3 2 36 6S m m m       ， ∴当 2 3m  时， S 取最大值，此时， 2QE  ，  2,2 3Q 又∵点 D 在抛物线 2 23 3 9 33 4 3 ( 1)2 2 2y x x x        上； 当 4 3y = 时， 2x  ， D∴ 的坐标为 2,4 3 ， F 的坐标为 9 31, 2       . 设 M 的坐标为 1, y ，则 / /MF DQ ∴当 MF DQ 时，以 M 、Q 、 D 、 F 为顶点的四边形是平行四边形. 由 9 3 4 3 2 32y    ， 解得： 13 3 2y  或 5 3 2y  ； ∴符合条件的点 M 的坐标为： 13 31, 2       ， 5 31, 2       . 【点睛】本题考查了二次函数的性质，二次函数的最值问题，求二次函数的解析式，平行四边 形的性质，以及解一元一次方程，解题的关键是熟练掌握二次函数的性质，熟练运用数形结合 的思想进行解题. 38．如图，AB 是半圆 O 的直径，半径 OC⊥AB，OB＝4，D 是 OB 的中点，点 E 是弧 BC 上的动点，连接 AE，DE． （1）当点 E 是弧 BC 的中点时，求△ADE 的面积； （2）若 3tan 2AED  ，求 AE 的长； （3）点 F 是半径 OC 上一动点，设点 E 到直线 OC 的距离为 m，当△DEF 是等腰直角三角 形时，求 m 的值. 【答案】（1） 6 2ADES  ；（2） 16 55AE  ；（3） 2 3m  ， 2 2m  ， 7 1m   . 【解析】（1）作 EH⊥AB，连接 OE，EB，设 DH＝a，则 HB＝2﹣a，OH＝2+a，则 EH＝OH ＝2+a，根据 Rt△AEB 中，EH2＝AH•BH，即可求出 a 的值，即可求出 S△ADE 的值； （2）作 DF⊥AE，垂足为 F，连接 BE，设 EF＝2x，DF＝3x，根据 DF∥BE 故 AF AD EF BD  ，得 出 AF＝6x，再利用 Rt△AFD 中，AF2+DF2＝AD2，即可求出 x，进而求出 AE 的长； （3）根据等腰直角三角形的不同顶点进行分类讨论，分别求出 m 的值. 【详解】解：（1）如图，作 EH⊥AB，连接 OE，EB， 设 DH＝a，则 HB＝2﹣a，OH＝2+a， ∵点 E 是弧 BC 中点， ∴∠COE＝∠EOH＝45°， ∴EH＝OH＝2+a， 在 Rt△AEB 中，EH2＝AH•BH， （2+a）2＝（6+a）（2﹣a）， 解得 a＝ 2 2 2  ， ∴a＝ 2 2 2 ， EH=2 2 ， S△ADE＝ 1 6 22 AD EH  ; （2）如图，作 DF⊥AE，垂足为 F，连接 BE 设 EF＝2x，DF＝3x ∵DF∥BE ∴ AF AD EF BD  ∴ 6 2 2 AF x  =3 ∴AF＝6x 在 Rt△AFD 中，AF2+DF2＝AD2 （6x）2+（3x）2＝（6）2 解得 x＝ 2 55 AE＝8x＝16 55 （3）当点 D 为等腰直角三角形直角顶点时，如图 设 DH＝a 由 DF=DE,∠DOF=∠EHD=90°，∠FDO+∠DFO=∠FDO+∠EDH， ∴∠DFO=∠EDH ∴△ODF≌△HED ∴OD＝EH＝2 在 Rt△ABE 中，EH2＝AH•BH （2）2＝（6+a）•（2﹣a） 解得 a＝± 2 3 2 m＝ 2 3 当点 E 为等腰直角三角形直角顶点时，如图 同理得△EFG≌△DEH 设 DH＝a，则 GE＝a，EH＝FG＝2+a 在 Rt△ABE 中，EH2＝AH•BH （2+a）2＝（6+a）（2﹣a） 解得 a＝ 2 2 2  ∴m＝ 2 2 当点 F 为等腰直角三角形直角顶点时，如图 同理得△EFM≌△FDO 设 OF＝a，则 ME＝a，MF＝OD＝2 ∴EH＝a+2 在 Rt△ABE 中，EH2＝AH•BH （a+2）2＝（4+a）•（4﹣a） 解得 a＝± 7 1 m＝ 7 1 【点睛】此题主要考查圆内综合问题，解题的关键是熟知全等三角形、等腰三角形、相似三角 形的判定与性质. 39．如图，在平面直角坐标系中，点 B 的坐标是 0,2 ，动点 A从原点 O 出发，沿着 x 轴正方 向移动，以 AB 为斜边在第一象限内作等腰直角三角形 ABP ，设动点 A的坐标为   ,0 0t t  . (1)当 2t  时，点 P 的坐标是 ；当 1t  时，点 P 的坐标是 ； (2)求出点 P 的坐标(用含t 的代数式表示)； (3)已知点C 的坐标为 1,1 ，连接 PC 、 BC ，过点 P 作 PQ y 轴于点Q ，求当t 为何值时，当 PQB 与 PCB 全等. 【答案】(1) (2，2)；( 3 2 ， 3 2 )； (2) P( 2 t 2  ， 2 t 2  )；(3) 2 2+2. 【解析】(1) 当 2t  时，三角形 AOB 为等腰直角三角形， 所以四边形 OAPB 为正方形，直 接写出结果；当 1t  时，作 PN⊥y 轴于 N，作 PM⊥x 轴与 M，求出△BNP≌△AMP，即可得 到 ON+OM=OB-BN+OA+AM=OB+OA，即可求出； (2) 作 PE⊥y 轴于 E，PF⊥x 轴于 F，求出△BEP≌△AFP，即可得到 OE+OF=OB+BE+OA+AF=OB+OA，即可求出； (3) 根据已知求出 BC 值，根据上问得到 OQ= 2 t 2  ，△PQB≌△PCB，BQ=BC，因为 OQ=BQ+OB，即可求出 t. 【详解】(1) 当 2t  时，三角形 AOB 为等腰直角三角形如图 所以四边形 OAPB 为正方形，所以 P(2，2) 当 1t  时，如图 作 PN⊥y 轴于 N，作 PM⊥x 轴与 M ∴四边形 OMPN 为矩形 ∵∠BPN+∠NPA=∠APM+∠NPA=90° ∴ ∠BPN =∠APM ∵∠BNP=∠AMP ∴ △BNP≌△AMP ∴PN=PM BN=AM ∴四边形 OMPN 为正方形，OM=ON=PN=PM ∴ON+OM=OB-BN+OA+AM=OB+OA=2+1=3 ∴OM=ON=PN=PM= 3 2 ∴ P( 3 2 ， 3 2 ) (2) 如图 作 PE⊥y 轴于 E，PF⊥x 轴于 F，则四边形 OEPF 为矩形 ∵∠BPE+∠BPF=∠APF+∠BPF=90° ∴ ∠BPE =∠APF ∵∠BEP=∠AFP ∴ △BEP≌△AFP ∴PE=PF BE=AF ∴四边形 OEPF 为正方形，OE=OF=PE=PF ∴OE+OF=OB+BE+OA+AF=OB+OA=2+t ∴ OE=OF=PE=PF= 2 t 2  ∴ P( 2 t 2  ， 2 t 2  )； (3) 根据题意作 PQ⊥y 轴于 Q，作 PG⊥x 轴与 G ∵ B(0，2) C(1，1) ∴ BC= 2 由上问可知 P( 2 t 2  ， 2 t 2  )，OQ= 2 t 2  ∵△PQB≌△PCB ∴BC=QB= 2 ∴ OQ=BQ+OB= 2 +2= 2 t 2  解得 t=2 2+2. 【点睛】此题主要考查了正方形的性质、全等三角形、直角坐标系等概念，关键是作出正方形 求出相应的全等三角形. 40．如图所示抛物线 2y ax bx c   过点  1,0A  ，点  0,3C ，且OB OC （1）求抛物线的解析式及其对称轴； （2）点 ,D E 在直线 1x  上的两个动点，且 1DE  ，点 D 在点 E 的上方，求四边形 ACDE 的周 长的最小值； （3）点 P 为抛物线上一点，连接CP ，直线CP 把四边形CBPA的面积分为 3∶5 两部分，求点 P 的坐标. 【答案】（1） 2y x 2x 3    ，对称轴为直线 1x  ；（2）四边形 ACDE 的周长最小值为 10 13 1  ；（3） 1 2(4, 5) , (8, 45)P P  【解析】（1）OB=OC，则点 B（3，0），则抛物线的表达式为：y=a（x+1）（x-3）=a（x2-2x-3） =ax2-2ax-3a，即可求解； （2）CD+AE=A′D+DC′，则当 A′、D、C′三点共线时，CD+AE=A′D+DC′最小， 周长也最小，即可求解； （3）S△PCB：S△PCA= 1 2 EB×（yC-yP）： 1 2 AE×（yC-yP）=BE：AE，即可求解． 【详解】（1）∵OB=OC，∴点 B（3，0）， 则抛物线的表达式为：y=a（x+1）（x-3）=a（x2-2x-3）=ax2-2ax-3a， 故-3a=3，解得：a=-1， 故抛物线的表达式为：y=-x2+2x+3…①； 对称轴为：直线 1x  （2）ACDE 的周长=AC+DE+CD+AE，其中 AC= 10 、DE=1 是常数， 故 CD+AE 最小时，周长最小， 取点 C 关于函数对称点 C（2，3），则 CD=C′D， 取点 A′（-1，1），则 A′D=AE， 故：CD+AE=A′D+DC′，则当 A′、D、C′三点共线时，CD+AE=A′D+DC′最小，周 长也最小， 四边形 ACDE 的周长的最小值 =AC+DE+CD+AE= 10 +1+A′D+DC′= 10 +1+A′C′= 10 +1+ 13 ； （3）如图，设直线 CP 交 x 轴于点 E， 直线 CP 把四边形 CBPA 的面积分为 3：5 两部分， 又∵S△PCB：S△PCA= 1 2 EB×（yC-yP）： 1 2 AE×（yC-yP）=BE：AE， 则 BE：AE，=3：5 或 5：3， 则 AE= 5 2 或 3 2 ， 即：点 E 的坐标为（ 3 2 ，0）或（ 1 2 ，0）， 将点 E、C 的坐标代入一次函数表达式：y=kx+3， 解得：k=-6 或-2， 故直线 CP 的表达式为：y=-2x+3 或 y=-6x+3…② 联立①②并解得：x=4 或 8（不合题意值已舍去）， 故点 P 的坐标为（4，-5）或（8，-45）． 【点睛】本题考查的是二次函数综合运用，涉及到一次函数、图象面积计算、点的对称性等， 其中（1），通过确定点 A′点来求最小值，是本题的难点． 41．如图，在 Rt ABC 中， C 90   ，AC 8cm ，BC 6cm ．现在有动点 P 从点 B 出发，沿 线段 BA 向终点 A 运动，动点Q从点 A 出发，沿折线 AC CB 向终点运动．如果点 P 的速度是 1cm / 秒，点Q的速度是2cm / 秒．它们同时出发，当有一点到达终点时，另一点也停止运动．设 运动的时间为 t 秒．  1 如图1，Q在 AC上，当 t 为多少秒时，以点 A 、 P 、Q 为顶点的三角形与 ABC相似？  2 如图2 ，Q在CB上，是否存着某时刻，使得以点 B 、P 、Q为顶点的三角形与 ABC相似？ 若存在，求出 t 的值；若不存在，请说明理由． 【答案】（1） 20t 7  或 50 13 ；（2）存在； 70t 13  . 【解析】(1)如图 1（1）,当∠AQP=90°时, AQP ACB∽ ,由相似三角形的性质就可以求出 t 值,如图 1(2)当∠APQ=90°时,就有 AQP ACB∽ ,由相似三角形的性质就可以求出其 t 值; (2)如图 2,当 BPQ BAC∽ 时根据相似三角形的性质就有 BP BQ AB BC  ,再根据已知条件就可以 求出 t 的值. 【详解】解： 1 如图  1 1 ，当 AQP 90   时， AQP ACB∽ ， ∴ AQ AP AC AB  ． 在 Rt ABC 中，由勾股定理，得 AB 36 64 10   ． BP t ， AQ 2t ， ∴ PA 10 t  ， ∴ 2t 10 t 8 10  ， ∴ 20t 7  ， 如图  1 2 ，当 APQ 90   时， APQ ACB∽ ， ∴ AQ AP AB AC  ， ∴ 2t 10 t 10 8  ， 50t 13  ． 综上所述， 20t 7  或 50 13 时，以点 A 、 P 、Q为顶点的三角形与 ABC相似；  2 如图2 ，当 BPQ BAC∽ 时， BP BQ AB BC  ． ∵ BQ 14 2t  ， BP t ， ∴ t 14 2t 10 6  ， 70t 13  ， ∴ 70t 13  时，Q在CB上，以点 B 、 P 、Q 为顶点的三角形与 ABC相似． 【点睛】本题是一道关于动点问题的相似三角形的综合试题,考查了勾股定理的运用,相似三角 形的判定及性质的运用,求出时间 t 而求证三角形相似是解题关键. 42．如图，在平面直角坐标系中，点 A 的坐标为（ ， ），点 B 在 轴正半轴上，∠ABO=30°， 动点 D 从点 A 出发，沿着射线 AB 方向以每秒 3 个单位的速度运动，过点 D 作 DE⊥ 轴，交 轴于点 E，同时，动点 F 从定点 C（ ， ）出发沿 轴正方向以每秒 1 个单位的速度运动，连 结 DO，EF，设运动时间为 秒. （1）当点 D 运动到线段 AB 的中点时， ①求 的值； ②判断四边形 DOFE 是否是平行四边形，请说明理由； （2）点 D 在运动过程中，以点 D，O，F，E 为顶点的四边形是矩形，求出满足条件的 的值； （3）过定点 C 做直线 ⊥ 轴，与线段 DE 所在的直线相交于点 M，连结 EC，MF，若四边 形 ECFM 为平行四边形，请直接写出点 E 的坐标. 【答案】（1）①t=2；②见解析；（2）t=14；（3）E （0， ）． 【解析】(1) ①由题意可知 ，当点 D 运动到线段 AB 的中点时，可知 ,由动点 D 的速度，可计算出 ； ②根据 轴，可知 轴，由点 F 的运动速度可知 ,推出 ，所以 DE 平行且等于 OF，可证出四边形 DOFE 是平行四边形. (2)由题意可知当点 D 在线段 AB 上，四边形 DOFE 构不成矩形，所以计算当点 D 在线段 AB 的延长线上，根据 ,可推出 ，因为四边形 DOFE 要构成 矩形，所以使 即可求出答案. (3)当点 D 在线段 AB 上运动时，由 可知 ，推出 ，因为四边形 ECFM 为平行四边形，所以 时成立，即可算出点 E 的坐 标；当点 D 在 AB 的延长线上，四边形 ECFM 不可能为平行四边形. 【详解】（1）①∵ ∴ ， ∵ 为 的中点， ∴ ， ∵点 的运动速度为每秒 个单位 ∴ ， 得： . ②∵ 轴，，可知 轴， 根据点 的运动速度与 ，可知 ， ∴ ∵ 为 的中点， ∴ 为 的中位线， ∴ ∴ ∴四边形 是平行四边形. （2）要使以点 为顶点的四边形是矩形，则点 在 射线上， 如下图所示： ∵ ∴ ∵ ， ∴ 即 ∴ （3）由题意可分情况讨论： 当点 D 在线段 AB 上运动时，如下图所示： ∵ ∴ ∵四边形 为平行四边形 ∴ ∴ ， ∵ ∴ ∴点 的坐标为 当点 在 的延长线上，四边形 ECFM 不可能为平行四边形 所以综上所述：点 的坐标为 【点睛】本题考查了平面直角坐标系里的动点问题，结合特殊四边形，熟知和掌握坐标与线段 的转化和矩形平行四边形的性质是解题关键. 43．如图，在平面直角坐标系中，抛物线 y＝﹣x2+bx+c 经过点 A（﹣1，0）和点 C（0，4）， 交 x 轴正半轴于点 B，连接 AC，点 E 是线段 OB 上一动点（不与点 O，B 重合），以 OE 为边 在 x 轴上方作正方形 OEFG，连接 FB，将线段 FB 绕点 F 逆时针旋转 90°，得到线段 FP，过 点 P 作 PH∥y 轴，PH 交抛物线于点 H，设点 E（a，0）． （1）求抛物线的解析式． （2）若△AOC 与△FEB 相似，求 a 的值． （3）当 PH＝2 时，求点 P 的坐标． 【答案】（1）y＝﹣x2+3x+4；（2）a＝16 5 或 4 5 ；（3）点 P 的坐标为（2，4）或（1，4）或（ 3+ 17 2 ， 4）． 【解析】 【详解】（1）点 C（0，4），则 c＝4， 二次函数表达式为：y＝﹣x2+bx+4， 将点 A 的坐标代入上式得：0＝﹣1﹣b+4，解得：b＝3， 故抛物线的表达式为：y＝﹣x2+3x+4； （2）tan∠ACO＝ AO CO ＝ 1 4 ， △AOC 与△FEB 相似，则∠FBE＝∠ACO 或∠CAO， 即：tan∠FEB＝ 1 4 或 4， ∵四边形 OEFG 为正方形，则 FE＝OE＝a， EB＝4﹣a， 则 1 4 4 a a  或 44 a a  ， 解得：a＝16 5 或 4 5 ； （3）令 y＝﹣x2+3x+4＝0，解得：x＝4 或﹣1，故点 B（4，0）； 分别延长 CF、HP 交于点 N， ∵∠PFN+∠BFN＝90°，∠FPN+∠PFN＝90°， ∴∠FPN＝∠NFB， ∵GN∥x 轴，∴∠FPN＝∠NFB＝∠FBE， ∵∠PNF＝∠BEF＝90°，FP＝FB， ∴△PNF≌△BEF（AAS）， ∴FN＝FE＝a，PN＝EB＝4﹣a， ∴点 P（2a，4），点 H（2a，﹣4a2+6a+4）， ∵PH＝2， 即：﹣4a2+6a+4﹣4＝|2|， 解得：a＝1 或 1 2 或 3 17 4  或 3 17 4  （舍去）， 故：点 P 的坐标为（2，4）或（1，4）或（ 3+ 17 2 ，4）． 【点睛】本题考查的是二次函数综合运用，其中（2）、（3），要注意分类求解，避免遗漏． 44．如图，矩形 OABC 的顶点 O、 A、C 都在坐标轴上，点 B 的坐标为  8,3 ， M 是 BC 边的中点． （1）求出点 M 的坐标和 COM 的周长；（直接写出结果） （2）若点 Q 是矩形 OABC 的对称轴 MN 上的一点，使以 O、 M 、C 、Q 为顶点的四 边形是平行四边形，求出符合条件的点 Q 的坐标； （3）若 P 是 OA 边上一个动点，它以每秒 1 个单位长度的速度从 A 点出发，沿 AO 方 向向点 O 匀速运动，设运动时间为 t 秒．是否存在某一时刻，使以 P 、O、M 为顶点的 三角形与 COM 相似或全等? 若存在，求出此时 t 的值；若不存在，请说明理由． 【答案】(1)  4,3M ，周长为12；(2) 4,6 ， 4,0 ；(3)存在， 7 s4 或 4s. 【解析】(1)根据四边形 OABC 是矩形和 M 是 BC 边的中点，求出点 M 的坐标，根据勾股定 理求出 OM 的长，得到△COM 的周长； (2)分以 OC，OM 为边的平行四边形 COMQ 和以 OC，CM 为边的平行四边形 COQM 两种 情况讨论即可； (3)分∠PMO=90º和∠MPO=90º两种情况，根据相似或全等三角形的性质解答即可． 【详解】解：(1)四边形OABC 是矩形， CB OA ，CB OA ．  8,3B ， M 为 BC 中点，  4,3M ， 3OC AB  ， 1 42CM BC  ． 在 Rt OMC 中， 90C   ， 2 2 2 23 4 5OM OC CM      ． OMC 的周长 3 4 5 12OM CM CO       ． 点  4,3M ， OMC 的周长为12． (2)分情况讨论： 当四边形是以OC ，OM 为边的平行四边形COMQ ， 则 MQ OC ， 3MQ OC  ．此时  4,6Q ； 当四边形是以OC ，CM 为边的平行四边形COMQ ， 则Q 点是对称轴 MN 与 x 轴的交点，此时  4,0Q ； 综上所述，符合条件的点Q 的坐标为 4,6 ， 4,0 ． (3)存在． 如图．由题意知 MOP 不可能等于90，分两种情况： 当 90PMO   时， OMP MCO∽ ， OM OP MC MO   ． 2 25 25 4 4 OMOP MC     ． 7 4AP OA OP    ．  7 s4t  ． 当 90MPO   时， OMP MOC≌ ， 4OP MC   ． 8 4 4AP OA OP      ．  4 st  ． 综上所述，当为 7 s4 或 4s时， OMP 与 MOC 相似或全等． 故答案为(1)  4,3M ，周长为12；(2) 4,6 ， 4,0 ；(3)存在， 7 s4 或 4s. 【点睛】本题是一道四边形综合题，主要考查了平行四边形、矩形的性质，全等三角形的判定 和性质，相似三角形的判定和性质. 45．如图，在△ABC 中，已知 3 4 90    ， ，AC cm BC cm BCA ，直线 , CM BC CD AB ， 动点 E 从点 C 开始沿射线 CB 方向以每秒 2cm 的速度运动，动点 F 也同时从点 C 开始在直线 CM 上以每秒1cm 的速度运动，R 是线段 AB 上任意一点，设运动时间为 t( 0)t 秒. （1）求 CD 的长. （2）当 t 为多少时， ABE 为等腰三角形？ （3）当 t 为多少时， EBR 与 DCF 全等，并简要说明理由. 【答案】（1）12 5 ；（2）t= 7 16 或 4.5 秒；（3）t= 4 3 或 4 5 或 4 或16 5 秒. 【解析】（1）由勾股定理，可得： 5AB cm ，根据面积法，即可求得 CD 的值； （2）当 ABE 为等腰三角形，分两种情况讨论：① 若 AE=BE 时，②若 AB=BE 时，分别求出 t 的值，即可； （3）当 EBR 与 DCF 全等时，分 4 种情况讨论：(I)当点 E 在线段 BC 上时，点 F 在线段 AC 上时，①若∆BRE≅∆CDF，②若∆BRE≅∆CFD，(II)当点 E 在射线 BE 上时，点 F 在射线 CF 上时， ①若∆BRE≅∆CDF，②若∆BRE≅∆CFD，分别求出 t 的值，即可. 【详解】（1）∵ 3 4 90    ， ，AC cm BC cm BCA ， ∴ 2 2 2 23 4 5AB AC BC cm     ， ∵CD AB ， ∴ 3 4 12 5 5 AC BCCD AB     cm； （2）当 ABE 为等腰三角形，分两种情况讨论： ① 若 AE=BE 时，如图 1， ∵动点 E 从点 C 开始沿射线 CB 方向以每秒 2cm 的速度运动，运动时间为 t( 0)t 秒， ∴CE=2t，AE=BE=4-2t， 在 Rt∆ACE 中， ∵ 2 2 2AC CE AE  ， ∴ 2 2 23 (2 ) (4 2 )t t   ，解得：t= 7 16 ， ②若 AB=BE 时，如图 2， ∵动点 E 从点 C 开始沿射线 CB 方向以每秒 2cm 的速度运动，运动时间为 t( 0)t 秒， ∴BE=2t-4， ∴2t-4=5，解得：t=4.5， 综上所述：当 t= 7 16 或 4.5 秒， ABE 为等腰三角形； （3）(I)当点 E 在线段 BC 上时，点 F 在线段 AC 上时， 则 BE=4-2t，CF=t， ∵∠ACB=90°，CD⊥AB， ∴∠ACD+∠BCD=∠ABC+∠BCD， ∴∠ACD=∠ABC， ①若∆BRE≅∆CDF，如图 3， ∴BE=CF，BR=CD=12 5 cm， 即： 4-2t=t，解得：t= 4 3 ， ②若∆BRE≅∆CFD，如图 4， ∴BE=CD=12 5 cm，BR=CF， 即：4-2t=12 5 ，解得：t= 4 5 ， 此时，BR=CF= 4 5 ×1= 4 5 cm； (II)当点 E 在 B 点的左侧时，点 F 在点 C 下时， 则 BE=2t-4，CF=t， ∵∠ACD=∠ABC， ∴∠ABE=∠DCF 若①若∆BRE≅∆CDF，如图 5， ∴BE=CF，BR=CD=12 5 cm， 即：2t-4=t，解得：t=4， ②若∆BRE≅∆CFD，如图 6， ∴BE=CD=12 5 cm，BR=CF， 即：2t-4=12 5 ，解得：t=16 5 ， 此时，BR=CF=16 5 ×1=16 5 cm，点 R 与点 D 重合； 综上所述：当 t= 4 3 或 4 5 或 4 或16 5 秒， EBR 与 DCF 全等. 【点睛】本题主要考查直角三角形的性质，等腰三角形的性质以及全等三角形的性质的综合应 用，根据题意，分类讨论，列出方程求解，是解题的关键. 46．（1）如图 1，Rt MBC 中， 90MCB   ，点 M 在数轴-1 处，点C 在数轴 1 处，MA MB ， 1BC  ，则数轴上点 A对应的数是 ． （2）如图 2，点 M 是直线 2 3y x  上的动点，过点 M 作 MN 垂直 x 轴于点 N ，点 P 是 y 轴上 的动点，当以 M ， N ， P 为顶点的三角形为等腰直角三角形时点 M 的坐标为 ． 【答案】（1） 5 1 ；（2）M 坐标是（-3，-3），（-1，1），（ 3 4  ， 3 2 ）． 【解析】（1）通过勾股定理求出线段 MB，而线段 MA=MB，进而知道点 A 对应的数，减去 1 即可得出答案． （2）分四种情况考虑：当 M 运动到（-1，1）时，ON=1，MN=1，由 MN⊥x 轴，以及 ON=MN； 又当 M 运动到第三象限时，要 MN=MP，且 PM⊥MN 时；若 MN 为斜边时，则∠ONP=45°， 所以 ON=OP，求出此时 M 坐标；又当点 M′在第二象限，M′N′为斜边时，这时 N′P=M′P，∠M′N′P=45°，求出此时 M 坐标，综上，得到所有满足题意 M 的坐标． 【详解】解：在 Rt△MBC 中，∠MCB=90°， ∴ 2 2MB MC BC= + ∴ 5MB ， ∵MA=MB， ∴ 5MA  ， ∵点 M 在数轴-1 处， ∴数轴上点 A 对应的数是 5 1 ； （2）①如图 1， 当 M 运动到（-1，1）时，ON=1，MN=1， ∵MN⊥x 轴，所以由 ON=MN 可知，△MNP 为等腰直角三角形； ②如图 2， 当 M 运动到第三象限时，要 MN=MP，且 PM⊥MN， 设点 M（x，2x+3），则有：-x=-（2x+3）， 解得：x=-3， 所以点 M 坐标为（-3，-3）． 若 MN 为斜边时，则∠ONP=45°，所以 ON=OP，设点 M（x，2x+3）， 则有 ( )1 2 2 3x x- = - + ，化简得-2x=-2x-3， 这方程无解，所以这时不存在符合条件的 M 点； ③如图 2， ∵当点 M′在第二象限，M′N′为斜边时，这时 N′P=M′P，∠M′N′P=45°， 设点 M′（x，2x+3），则 OP=ON′，而 1 2OP M N= ⅱ ， ∴有 ( )1 2 2 3x x- = + ， 解得： 3 4x   ， ∴M′（ 3 4  ， 3 2 ）， 综上，符合条件的点 M 坐标是（-3，-3），（-1，1），（ 3 4  ， 3 2 ）． 【点睛】此题考察了实数与数轴，通过勾股定理，在数轴寻找无理数和一次函数综合题，涉及 的知识有：实数与数轴，等腰直角三角形的性质，坐标与图形性质，利用了分类讨论的思想， 分类讨论时注意考虑问题要全面，做到不重不漏．