中考中折叠型问题教学设计

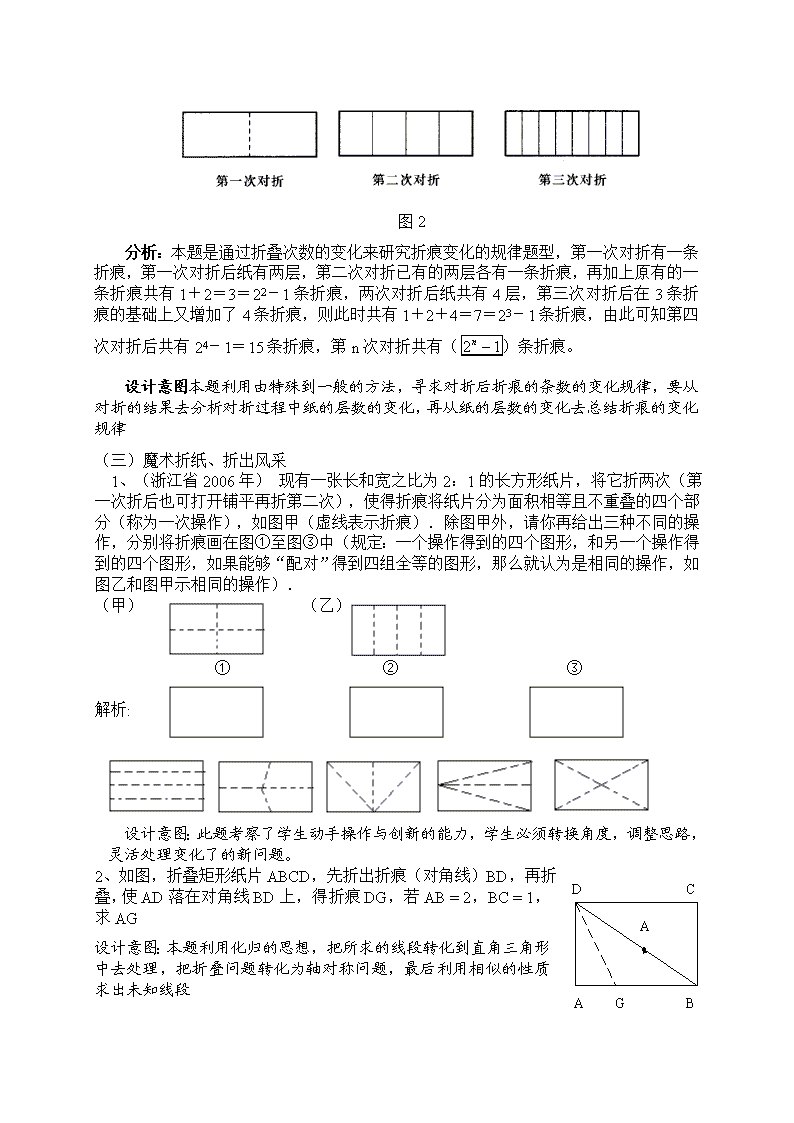
中考中折叠型问题教学设计

折叠与剪拼问题的教学设计 一、教材分析：图形的折叠问题是图形变换的一种，折叠型问题立意新颖，变幻巧妙，对培养学生的识图能力及灵活运用数学知识解决问题的能力非常有效。有关折叠问题在近几年各地中考中也频频出现，主要是考查学生的自主探索能力与空间想象能力以及判断推理能力。‎ 二、教学目标：‎ 知识与技能目标：把握图形折叠问题的实质，分清折叠前后哪些元素没变，哪些元素变化，理解折叠前后关于折痕成轴对称图形。通过动手操作掌握寻找折痕条数的规律、掌握图形折叠后求折痕长度的方法、掌握图形剪拼的方法 过程与方法：采用小组合作探究与动手实践相结合的教学模式，使学生学会与他人交流思维过程和结果，在动手实践中使学生的逆向思维和发散思维的到发展，自主探索能力与空间想象能力以及判断推理能力得以提高 情感态度与价值观：在小组的讨论与交流中培养学生的合作意识，在动手实践中激发学生兴趣，通过折叠问题的研究，使学生明确事物的变化与统一，理解事物的联系与区别 三、教学重点：把握折叠与拼图的实质，并利用它与轴对称、全等三角形、相似三角形、勾股定理、矩形的判定等联系在一起，提高学生的分析问题、解决问题的能力。‎ 四、教学难点：把握折叠的变化规律，运用所学知识合理、有序、全面的解决问题 五、教学方法：‎ 在教学过程中注重学生的亲身实践，注重学生能力的培养，采用小组合作探究与动手实践相结合的教学模式，充分尊重学生的主体地位，‎ 六、学法指导 数与形是一对孪生姐妹，要学好数学就要学生的数与形结合起来，把动手得到的图形转变成几何图形 七、设计理念：‎ ‎ 21世纪的教育要以人为本，，在教学过程中充分尊重学生的主体地位，注重学生的亲身实践，注重学生能力的培养。本节课我始终让学生分组合作和动手实践，使学生在合作中思维过程得以展现，思维结果得以肯定。图形的剪拼使学生把所拼剪的图形画在纸上，体现数学的数形结合思想，使学生的空间观念、动手能力及思维都有所发展 八、教学设计：‎ ‎（一）游戏引入，激发兴趣 教师上课时拿出事先做好的纸船，让学生模仿着折叠一个 设计意图：通过折纸游戏激发学生兴趣，为本节课的教学埋下伏笔。并以此引出课题 ‎（二）亲自动手，探索规律 例1（2005年余姚市）将一张长方形的纸对折，如图2所示，可得到一条折痕（图中虚线），继续对折，对折时每次折痕与上次的折痕保持平行，连续对折三次后，可以得到7条折痕，那么对折四次可以得到________条折痕，如果对折n次，可以得到_________条折痕。‎ 图2‎ 分析：本题是通过折叠次数的变化来研究折痕变化的规律题型，第一次对折有一条折痕，第一次对折后纸有两层，第二次对折已有的两层各有一条折痕，再加上原有的一条折痕共有1＋2＝3＝22－1条折痕，两次对折后纸共有4层，第三次对折后在3条折痕的基础上又增加了4条折痕，则此时共有1＋2＋4＝7＝23－1条折痕，由此可知第四次对折后共有24－1＝15条折痕，第n次对折共有（）条折痕。‎ 设计意图本题利用由特殊到一般的方法，寻求对折后折痕的条数的变化规律，要从对折的结果去分析对折过程中纸的层数的变化，再从纸的层数的变化去总结折痕的变化规律 ‎（三）魔术折纸、折出风采 ‎1、（浙江省2006年） 现有一张长和宽之比为2：1的长方形纸片，将它折两次（第一次折后也可打开铺平再折第二次），使得折痕将纸片分为面积相等且不重叠的四个部分（称为一次操作），如图甲（虚线表示折痕）．除图甲外，请你再给出三种不同的操作，分别将折痕画在图①至图③中（规定：一个操作得到的四个图形，和另一个操作得到的四个图形，如果能够“配对”得到四组全等的图形，那么就认为是相同的操作，如图乙和图甲示相同的操作）．‎ ‎（甲） （乙）‎ ‎① ② ③‎ ‎ ‎ 解析: ‎ 设计意图：此题考察了学生动手操作与创新的能力，学生必须转换角度，调整思路，灵活处理变化了的新问题。‎ G A1‎ D A B C ‎2、如图，折叠矩形纸片ABCD，先折出折痕（对角线）BD，再折叠，使AD落在对角线BD上，得折痕DG，若AB = 2，BC = 1，求AG 设计意图：本题利用化归的思想，把所求的线段转化到直角三角形中去处理，把折叠问题转化为轴对称问题，最后利用相似的性质求出未知线段 ‎（四）综合应用，你最棒 已知如图，矩形ABCD中（图1），AD>AB，O为对角线的交点，过O作一直线分别交于BC、AD于N、M。（1）求证：梯形ABNM的面积等于梯形CDMN的面积；（2）如图2，当MN满足什么条件时，将矩形ABCD以MN为折痕，翻折后能使C点恰好与A点重合？（只写出满足的条件，不要求证明）（3）在（2）的条件下，若翻折后和重叠部分的面积是重叠部分面积的一半，求BN：NC的值。‎ 设计意图：考察了矩形的一些性质并提出证明的要求，训练学生思维的严密性，使学生知其然还知其所以然，第二问题的设计培养学生的逆向思维，使学生通过动手实践结果作为已知条件第三问题的设置主要考察利用折叠的性质解决问题的能力。‎ ‎（五）剪拼图形 闪烁智慧例 ‎1、（海淀区2006年）下列矩形中，按虚线剪开后，既能拼出平行四边形和梯形，又能拼出三角形的是图形. ________ （请填图形下面的代号）。‎ 设计意图：此题若学生把矩形纸按实际要求操作一下，培养学生的动手操作能力，学生可以从多个角度去思考，从而培养学生的发散思维 ‎2、我们观察下面的操作和图形会获得：“经过割补可以将直角三角形化为矩形的方法。”‎ 示例1如图（1）三角形ABC是直角三角形，∠ABC=90°,取AB的中点D，AC中点E,连接DE,将△ADE割补给△CEF的位置就得到矩形BCFD.‎ 问题1：画图并作必要的文字说明，将图（2）中的梯形割补成一个矩形。‎ 如图（3），△ABC是任意的一个三角形，过顶点A作对边BC上的高，这样就将△ABC化为两个直角三角形，Rt△AHC 和Rt△AHB。再用前面示例的方法，把任意△ABC化为矩形 问题2：画图并作必要的文字说明，将图（4）中的任意四边形割补成一个矩形D ‎H C G E F C B D A A C A B D A · DDDD D B C D E F A B 设计意图：这道题既考查了学生的阅读理解能力又考查了学生综合应用知识的能力。本题有特殊的图形入手，直到一般图形得到结论，体现数学的有特殊到一般的思想。在动手实践中使学生的观察能力、语言表述能力、空间想象力得到发展 ‎（六）秋收时节 硕果累累 通过本节课的动手操作，把你在本节课所学知识或体会或一些感想拿出来与大家分享 ‎（七）、课下复习 巩固成果贵阳市 ‎（必做题）(2006）年图1是正方体的一个平面展开图，如果折叠成原来的正方体时与边重合的是 （ ）‎ ‎（A） （B） ‎ ‎（C） （D） ‎ 答案：A 此题考察了学生的空间想象能力。‎ ‎（选做题）如图，在边长为2的菱形ABCD中，∠B=450，AE为BC边上的高，将ΔABE沿AE所在直线翻折得ΔAB1E，求ΔAB1E与四边形AECD重叠部分的面积。‎ 设计意图：体现课下作业的灵活性和分层教学设计要求，是不同层次的学生都有所收获