- 2021-05-10 发布 |
- 37.5 KB |
- 10页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考总复习二次函数小题难点突破
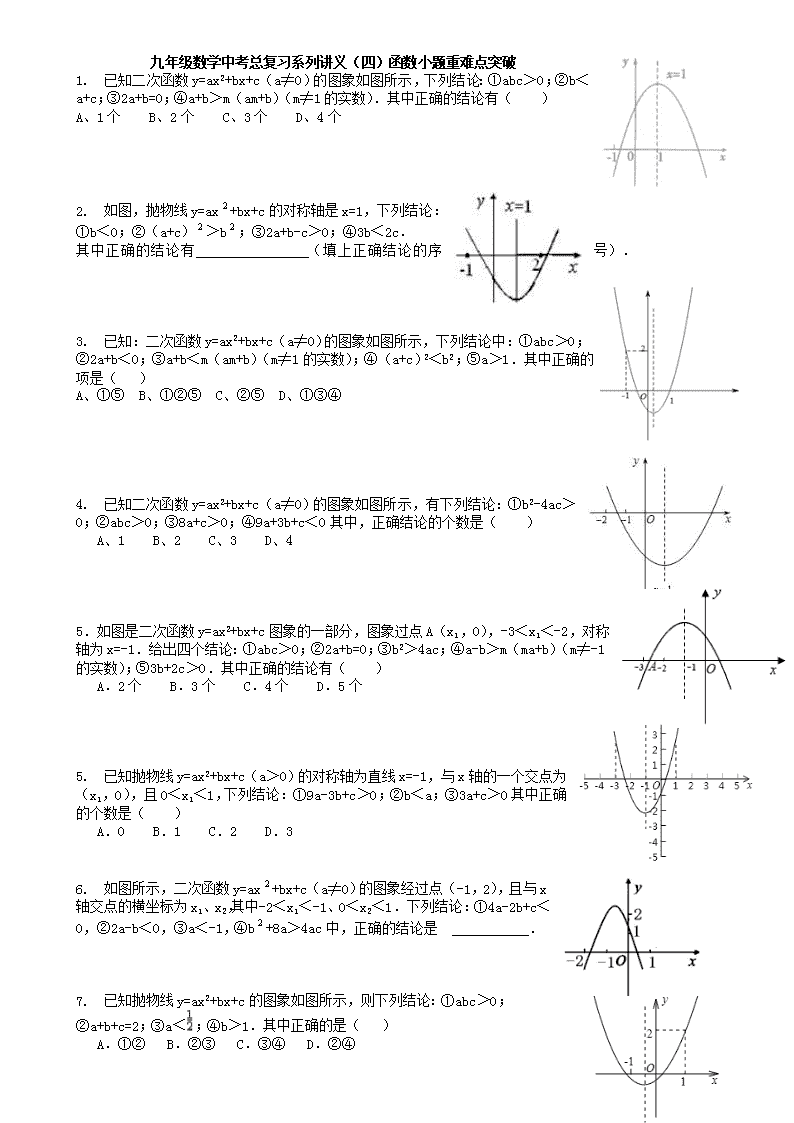
九年级数学中考总复习系列讲义(四)函数小题重难点突破 1. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②b<a+c;③2a+b=0;④a+b>m(am+b)(m≠1的实数).其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个 2. 如图,抛物线y=ax+bx+c的对称轴是x=1,下列结论: ①b<0;②(a+c)>b;③2a+b-c>0;④3b<2c. 其中正确的结论有 (填上正确结论的序号). 3. 已知:二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论中:①abc>0;②2a+b<0;③a+b<m(am+b)(m≠1的实数);④(a+c)2<b2;⑤a>1.其中正确的项是( ) A、①⑤ B、①②⑤ C、②⑤ D、①③④ 4. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①b2-4ac>0;②abc>0;③8a+c>0;④9a+3b+c<0其中,正确结论的个数是( ) A、1 B、2 C、3 D、4 5.如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(x1,0),-3<x1<-2,对称轴为x=-1.给出四个结论:①abc>0;②2a+b=0;③b2>4ac;④a-b>m(ma+b)(m≠-1的实数);⑤3b+2c>0.其中正确的结论有( ) A.2个 B.3个 C.4个 D.5个 5. 已知抛物线y=ax2+bx+c(a>0)的对称轴为直线x=-1,与x轴的一个交点为(x1,0),且0<x1<1,下列结论:①9a-3b+c>0;②b<a;③3a+c>0其中正确的个数是( ) A.0 B.1 C.2 D.3 6. 如图所示,二次函数y=ax+bx+c(a≠0)的图象经过点(-1,2),且与x轴交点的横坐标为x1、x2,其中-2<x1<-1、0<x2<1.下列结论:①4a-2b+c<0,②2a-b<0,③a<-1,④b+8a>4ac中,正确的结论是 . 7. 已知抛物线y=ax2+bx+c的图象如图所示,则下列结论:①abc>0;②a+b+c=2;③a<;④b>1.其中正确的是( ) A.①② B.②③ C.③④ D.②④ 1. 已知:抛物线y=ax2+bx+c(a<0)经过点(-1,0),且满足4a+2b+c>0,以下结论:①a+b>0;②a+c>0;③-a+b+c>0;④b2-2ac>5a2,其中正确的个数有( ) A.1个 B.2个 C.3个 D.4个 2. 如图,是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0), 对称轴为x=-1.给出四个结论:①b2>4ac;②b= -2a;③a-b+c=0;④b>5a. 其中正确结论是 ①④ . 3. 已知二次函数y=a(x﹣2)2+c,当x=x1时,函数值为y1;当x=x2时,函数值为y2, 若|x1﹣2|>|x2﹣2|,则下列表达式正确的是( ) A.y1+y2>0 B.y1﹣y2>0 C.a(y1﹣y2)>0 D.a(y1+y2)>0 4. 如图是抛物线()的部分图象,其顶点坐标为,且与轴的一个交点 在点和之间.则下列结论:①;②;③; ④一元二次方程有两个不相等的实数根.其中正确结论的个数是 A. B. C. D. 5. 以为自变量的二次函数的图象不经过第三象限,则实数的取值范围是( )。 A. B.或 C. D. 6. 函数与的图象如图所示,有以下结论:①; ②;③; ④当时,; 其中正确的个数是:( ) A.1 B.2 C.3 D.4 7. 如图,直线与双曲线 (k>0,x>0)交于点A,将直线向上 平移4个单位长度后,与y轴交于点C,与双曲线 (k>0,x>0)交于点B, 若OA=3BC,则k的值为______ 1. 用min{a,b,c}表示a,b,c,三个数中的最小值,设y=min{x^2,x+2,10-x}(x≥0),则y的最大值为( ) A.4 B.5 C.6 D.7 2. 如图,点A的坐标为(1,0),点B在直线上运动,当线段AB最短时, 点B的坐标为( ). (A)(0,0) (B)(,-)(C)(,-) (D)(-,) 3. 在反比例函数的图象中,阴影部分的面积不等于4的是( ) (A) (B) (C) (D) 第(12)题 4. 已知二次函数()的图象如图所示,有下列结论: ①; ②; ③; ④. 其中,正确结论的个数是 A.1 B.2 C.3 D.4 5. 二次函数的图象如图所示,下列结论: ①<0;②<0;③<0;④>0. 其中正确结论的个数是( ) (A)1 (B)2 (C)3 (D)4 C 6. 在平面直角坐标系中,将抛物线向上(下)或向左(右)平移个单位,使平移后的抛物线恰好经过原点,则的最小值为( ) (A)1 (B)2 (C)3 (D)6 7. 已知二次函数,其中,、()是方程的两个根,则实数、、、的大小关系是( ) (A) (B) (C) (D) 8. 如图,二次函数()的图象经过点(-1,2)且与轴交点的横坐标分别为、,其中-2<<-1,0<<1,下列结论: ①<0; ②<0; ③>1; ④>. 其中正确的有( ) (A)1个 (B)2个 (C)3个 (D)4个 9. 已知抛物线与轴的两个公共点之间的距离为1.若将抛物线 向上平移一个单位,则它与轴只有一个公共点;若将抛物线向下平移一个单位,则它经过原点.则抛物线为 (A) (B)或 (C) (D)或 1. 如图,已知A、B是线段MN上的两点,MN=4,MA=1,MB>1,以A 为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC,设AB=x. (Ⅰ)x的取值范围为 ; (II)△ABC的最大面积为 . 2. 下列命题: ①若,则; ②若,则一元二次方程有两个不相等的实数根; ③若,则一元二次方程有两个不相等的实数根; ④若,则二次函数的图象与坐标轴的公共点的个数是2或3. 其中正确的是( )(A) 只有①②③ (B) 只有①③④ (C) 只有①④ (D) 只有②③④. 3. 已知二次函数()的图象如图所示,对称轴为直线, 有下列结论:①<0;②<0;③<. 其中正确结论的个数是 (A)0 (B)1 (C)2 (D)3 4. 如图,边长为1的正方形的顶点为坐标原点,点在轴的正半轴上,点在轴的正半轴上.动点在边上移动(不与点,重合),连接,过点作,交边于点,连接.当线段的长度取得最小值时,点的纵坐标为( ) x 1 y 1 3 3 O (A)0 (B) (C) (D)1 5. 函数与的图象如图所示,有以下结论: ①;②;③; ④当时,; 其中正确的个数是( ) (A)1 (B)2 (C)3 (D)4 6. 二次函数y=x2-x+m(m为常数)的图象如图所示,当x=a时,y<0,那么当x=a-1时,函数值( ) (A)y<0 (B)0<y<m (C)y>m (D)y=m 7. 定义[a,b,c]为函数的特征数,现给出特征数为[2m,1-m,-1-m]的函数的一些结论:①当m=-3时,函数图象的顶点坐标是(,);②当m>0时,函数图象截x轴所得的线段长度大于;③当m<0时,函数在x>时,y随x的增大而减小;④当m≠0时,函数图象经过同一个点.其中正确的结论有( ) (A)①②③ (B)①②④ (C)①③④ (D)②③④ 8. 已知二次函数y=a(x﹣h)2+k在坐标平面上的图形通过(0,5)、(10,8)两点. 若a<0,0<h<10,则h的值可能为( ) (A)7 (B)5 (C)3 (D)2 x y 1 O 第(12)题 1. 如图是二次函数图象的一部分,对称轴是直线.有下列结论:①>;②<0;③<;④若点(,)与(,)是抛物线上的两点,则<.其中,正确的结论是 (A)①② (B)①③ (C)①③④ (D)②③④ 2. 已知二次函数中,函数与自变量的部分对应值如下表: … 0 1 2 3 … … 10 5 2 1 2 … 则当<5时,的取值范围是_________. 3. 若二次函数()的图象与x轴有两个交点,坐标分别为(,0)、(,0),且<,图象上有一点M(,)在x轴下方,则下列判断正确的是( ) (A)>0 (B) ≥0 (C)<< (D) <0 4. 已知二次函数(>0),当=时,相应的函数值大于0,那下列结论中正确的 是( ) (A)当时,相应的函数值小于0 (B)当时,相应的函数值大于0 (C)当时,相应的函数值等于0 (D)当时,相应的函数值与0的大小关系不确定 5. 已知反比例函数的图像如右图所示,则二次函数的图像大致为( ). 6. 已知a≠0,在同一直角坐标系中,函数y=ax与y=ax2的图象有可能是( ) A. B. C. D. 7. 已知二次函数y=kx2+(2k﹣1)x﹣1与x轴交点的横坐标为x1,x2(x1<x2),则对于下列结论: ①当x=﹣2时,y=1; ②方程kx2+(2k﹣1)x﹣1=0有两个不相等的实数根x1,x2; ③x2﹣x1=. 其中正确的结论有 (只需填写序号即可). 1. 如图,过y轴正半轴上的任意一点P,作x轴的平行线,分别与反比例函数的图象交于点A和点B,若点C是x轴上任意一点,连接AC、BC,则△ABC的面积为( ) A.3 B.4 C.5 D.6 2. 如图,直线y=﹣x+b(b>0)与双曲线y=(x>0)交于A、B两点,连接OA、OB,AM⊥y轴于M,BN⊥x轴于N;有以下结论:①OA=OB,②△AOM≌△BON,③若∠AOB=45°,则S△AOB=k, ④当AB=时,ON﹣BN=1;其中结论正确的个数为( ) A.1 B.2 C.3 D.4 3. 若一次函数y=kx+1的图象与反比例函数的图象没有公共点,则实数k的取值范围是 . 4. 如图,□ABCD的顶点A.B的坐标分别是A(﹣1,0),B(0,﹣2),顶点C.D 在双曲线y=上,边AD交y轴于点E,且四边形BCDE的面积是△ABE面积的5倍, 则k= . 5. 如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( ) A.乙前4秒行驶的路程为48米 B.在0到8秒内甲的速度每秒增加4米/秒 C.两车到第3秒时行驶的路程相等 D.在4至8秒内甲的速度都大于乙的速度 6. 在一次800米的长跑比赛中,甲、乙两人所跑的路程s(米)与各自所用时 间t(秒)之间的函数图象分别为线段OA和折线OBCD,则下列说法正确的是( ) A.甲的速度随时间的增加而增大 B.乙的平均速度比甲的平均速度大 C.在起跑后第180秒时,两人相遇 D.在起跑后第50秒时,乙在甲的前面 1. 如下左图,在矩形ABCD中,动点P从点B出发,沿BC,CD,DA运动至点A停止。设点P运动的路程为,△ABP的面积为,如果关于的函数图像如下右图所示,则△ABC的面积是( ) A.10 B.16 C.18 D.20 2. 如图,点E,F,G,H分别在菱形ABCD的四条边上,BE=BF=DG=DH,连接EF,FG,GH,HE,得到四边形EFGH,则四边形EFGH是 形;若AB=,∠A=60°,当BE= 时,四边形EFGH的面积最大。 3. 如图的一座拱桥,当水面宽AB为12m时,桥洞顶部离水面4m,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线解析式是y=﹣(x﹣6)2+4,则选取点B为坐标原点时的抛物线解析式是 . 4. 甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程s(米)与时间t(分钟)之间的函数关系如图所示,请你根据图像判断,下列说法正确的是( ) A.甲队率先到达终点 B.甲队比乙队多走了200米 C.乙队比甲队少用0.2分钟 D.比赛中两队从出发到2.2分钟时间段,乙队的速度比甲队的速度大 5. 下列四幅图像近似刻画两个变量之间的关系,请按图象顺序将下面四种情景与之对应排序( ) ①一辆汽车在公路上匀速行驶(汽车行驶的路程与时间的关系) ②向锥形瓶中匀速注水(水面的高度与注水时间的关系) ③将常温下的温度计插入一杯热水中(温度计的读书与时间的关系) ④一杯越来越凉的水(水温与时间的关系) A. ①②④③ B.③④②① C.①④②③ D.③②④① 1. 甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500m,先到终点的人原地休息.已知甲先出发2s.在跑步过程中,甲、乙两人的距离y(m)与乙出发的时间t(s)之间的关系如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是( ) A.①②③ B.仅有①② C.仅有①③ D.仅有②③ 2. 均匀地向一个容器注水,最后把容器注满,水面高度随时间的变化规律如图所示(图中为一折线),这个容器的形状是( ). (A) (B) (C) (D) 3. 小明的父母出去散步,从家走了20分钟到一个离家900米的报亭,母亲随即按原速度返回家.父亲在报亭看了10分报纸后,用15分钟返回家.则表示父亲、母亲离家距离与时间之间的关系的图象分别 是 (只需填写序号). 4. 一家电信公司给顾客提供两种上网收费方式:方式A以每分0.1元的价格按上网所用时间计算;方式B除收月基费20元外.再以每分0.05元的价格按上网所用时间计费。若上网所用时问为分.计费为元,如图.是在同一直角坐标系中.分别描述两种计费方式的函救的图象,有下列结论:① 图象甲描述的是方式A:② 图象乙描述的是方式B;③ 当上网所用时间为500分时,选择方式B省钱.其中,正确结论的个数是( ) (A) 3 (B) 2 (C) 1 (D) 0 5. 如图,是一对变量满足的函数关系的图象.有下列3个不同的 问题情境: ①小明骑车以400米/分的速度匀速骑了5分,在原地休息了4分,然后以500米/分的速度匀速骑回出发地,设时间为x分,离出发地的距离为y千米;②有一个容积为6升的开口空桶,小亮以1.2升/分的速度匀速向这个空桶注水,注5分后停止,等4分后,再以2升/分的速度匀速倒空桶中的水,设时间为x分,桶内的水量为y升;③矩形ABCD中,AB=4,BC=3,动点P从点A出发,依次沿对角线AC、边CD、边DA运动至点A停止,设点P的运动路程为x,当点P与点A不重合时,y=S△ABP;当点P与点A重合时,y=0. 其中,符合图中所示函数关系的问题情境的个数为( ) (A) 0 (B) 1 (C) 2 (D)3 1. 如图,在平行四边形ABCD中,AC = 4,BD = 6,P是BD上的任一点,过P作EF∥AC,与平行四边形的两条边分别交于点E,F.设BP=x,EF=y,则能大致反映y与x之间关系的图象为( ) A B C D 2. 小文、小亮从学校出发到青少年宫参加书法比赛,小文步行一段时间后,小亮骑自行车沿相同路线行进,两人均匀速前行.他们的路程差s(米)与小文出发时间t(分)之间的函数关系如图所示.下列说法:①小亮先到达青少年宫;②小亮的速度是小文速度的2.5倍;③;④.其中正确的是 (A)①②③ (B)①②④ (C)①③④ (D)①②③④ 3. 设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回.设秒后两车间的距离为千米,关于的函数关系如图所示,则甲车的速度是( ) A.10米/秒 B.15米/秒 C.20米/秒 D.25米/秒 4. 从甲地到乙地,先是一段平路,然后是一段上坡路.小明骑车从甲地出发,到达乙地后立即原路返回甲地,途中休息了一段时间.假设小明骑车在平路、上坡、下坡时分别保持匀速前进.已知小明骑车上坡的速度比在平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km.设小明出发h后,到达离甲地km的地方,图中的折线表示与之间的函数关系. 有下列说法: ①小明骑车在平路上的速度为15 km/h; ②小明途中休息了0.1 h; ③如果小明两次经过途中某一地点的时间间 隔为0.15 h,那么该地点离甲地5.75 km. 其中,正确的说法的个数是 (A)0 (B)1 (C)2 (D)3 5. 如图①,点是的中点,点在上,动点以每秒2cm的速度沿图①(90°)的边线运动,运动路径为:,相应的△的面积(cm2)关于运动时间t(s)的函数图象如图②,若cm,有下列结论: ①图①中的长是8cm; ②图②中的点表示第4秒时,的值为24cm2; ③图②中的点表示第12秒时,的值为18cm2. 其中,正确结论的个数是 (A)0 (B)1 (C)2 (D)3 1. 矩形ABCD中,AD=8cm,AB=6cm.动点E从点C开始沿边CB向点以2cm/s的速度运动至点B停止,动点F从点C同时出发沿边CD向点D以1cm/s的速度运动至点D停止.如图可得到矩形CFHE,设运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:),则y与x之间的函数关系用图象表示大致是下图中的 A查看更多