北师大版本数学九上1.2（直角三角形）中考演练2

北师大版本数学九上1.2（直角三角形）中考演练2

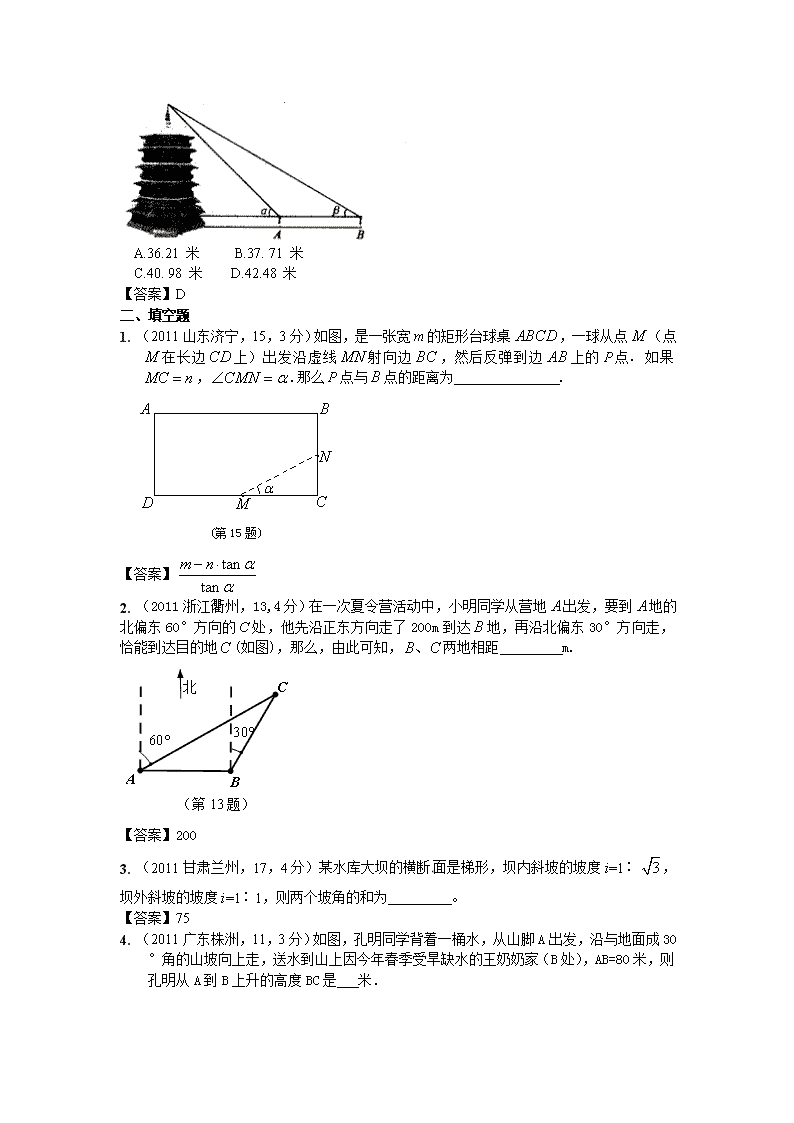
解直角三角形 一、选择题 ‎1. （2011湖北武汉市，10，3分）如图，铁路MN和公路PQ在点O处交汇，∠QON=30°．公路PQ上A处距离O点‎240米．如果火车行驶时，周围‎200米以内会受到噪音的影响．那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时，A处受噪音影响的时间为 ‎ A．12秒．  B．16秒．  C．20秒．  D．24秒．‎ ‎  ‎ ‎【答案】B ‎2. （2011湖南衡阳，9，3分）如图所示，河堤横断面迎水坡AB的坡比是1：，堤高BC=‎5m，则坡面AB的长度是（ ）‎ A．‎10m B．‎10‎m C．‎15m D．‎5‎m ‎ ‎【答案】A ‎3. （2011山东东营，8，3分）河堤横断面如图所示，堤高BC＝‎5米，迎水坡AB的坡比1：（坡比是坡面的铅直高度BC与水平宽度AC之比），则AC的长是（ ）‎ A．‎5‎米 B．‎10米 C．‎15米 D．‎10‎米 ‎【答案】A ‎4. （2010湖北孝感，10，3分）如图，某航天飞船在地球表面P点的正上方A处，从A处观测到地球上的最远点Q，若∠QAP=α，地球半径为R，则航天飞船距离地球表面的最近距离AP，以及P、Q两点间的地面距离分别是（ ）‎ A. ， B. ，‎ C. ， D. ，‎ ‎【答案】B ‎5. （2011宁波市，9，3分）如图，某游乐场一山顶滑梯的高为h，滑梯的坡角为a，那么滑梯长l为 ‎ A． B． C． D． h·sina ‎【答案】A ‎6. （2011台湾台北，34）图(十六)表示一个时钟的钟面垂直固定于水平桌面上，其中分针上有一点A，且当钟面显示3点30分时，分针垂直于桌面，A点距桌面的高度为‎10公分。如图(十七)，若此钟面显示3点45分时，A点距桌面的高度为‎16公分，则钟面显示3点50分时，A点距桌面的高度为多少公分？‎ A．　　B．　　C．18　　　D．19‎ ‎【答案】D ‎7. （2011山东潍坊，10，3分）身高相等的四名同学甲、乙、丙、丁参加风筝比赛，四人放出风筝的线长、线与地面的夹角如下表（假设风筝线是拉直的），则四名同学所放的风筝中最高的是（ ）‎ 同学 甲 乙 丙 丁 放出风筝线长 ‎140m ‎100m ‎95m ‎90m 线与地面夹角 ‎30°‎ ‎45°‎ ‎45°‎ ‎60°‎ A.甲 B.乙 C.丙 D.丁 ‎ ‎【答案】D ‎8. （2011四川绵阳10，3）周末，身高都为‎1.6米的小芳、小丽来到溪江公园，准备用她们所学的知识测算南塔的高度.如图，小芳站在A处测得她看塔顶的仰角α为45°，小丽站在B处测得她看塔顶的仰角β为30°.她们又测出A、B两点的距离为‎30米。假设她们的眼睛离头顶都为‎10cm，则 可计算出塔高约为(结果精确到0.01，参考数据：=1.414，=1.73)‎ A.‎36.21 米 B.37. ‎‎71 米 C.40. ‎98 米 D.42.48 米 ‎【答案】D 二、填空题 ‎1. （2011山东济宁，15，3分）如图，是一张宽的矩形台球桌，一球从点（点在长边上）出发沿虚线射向边，然后反弹到边上的点. 如果，.那么点与点的距离为 .‎ ‎ ‎ ‎·‎ ‎·‎ ‎(第15题)‎ ‎【答案】‎ ‎2. （2011浙江衢州，13,4分）在一次夏令营活动中，小明同学从营地出发，要到地的北偏东60°方向的处，他先沿正东方向走了‎200m到达地，再沿北偏东30°方向走，恰能到达目的地(如图)，那么，由此可知，两地相距 m. ‎ ‎（第13题）‎ ‎【答案】200‎ ‎3. （2011甘肃兰州，17，4分）某水库大坝的横断面是梯形，坝内斜坡的坡度i=1∶，坝外斜坡的坡度i=1∶1，则两个坡角的和为 。‎ ‎【答案】75‎ ‎4. （2011广东株洲，11，3分）如图，孔明同学背着一桶水，从山脚A出发，沿与地面成30°角的山坡向上走，送水到山上因今年春季受旱缺水的王奶奶家（B处），AB=‎80米，则孔明从A到B上升的高度BC是 米．‎ ‎【答案】40‎ ‎5. （2011浙江义乌，15，4分）右图是市民广场到解百地下通道的手扶电梯示意图．其 中AB、CD分别表示地下通道、市民广场电梯口处地面的水平线，∠ABC=135°，BC的长约是m，则乘电梯从点B到点C上升的高度h是 ▲ m． ‎ ‎135°‎ A B C D h ‎【答案】5‎ ‎6. (2011广东茂名，13，3分）如图，在高出海平面‎100米的悬崖顶A处，观测海平面上一艘小船B，并测得它的俯角为45°,则船与观测者之间的水平距离BC＝ 米．‎ ‎【答案】100‎ ‎7. （2011湖北襄阳，14，3分）在207国道襄阳段改造工程中，需沿AC方向开山修路（如图3所示），为了加快施工速度，需要在小山的另一边同时施工.从AC上的一点B取∠ABD＝140°，BD＝‎1000m，∠D＝50°.为了使开挖点E在直线AC上，那么DE＝ m.（供选用的三角函数值：sin50°＝0.7660，cos50°＝0.6428，tan50°＝1.192）‎ 图3‎ ‎【答案】642.8‎ ‎8. （2011内蒙古乌兰察布，16，4分）某厂家新开发的一种电动车如图，它的大灯A射出的光线AB,AC 与地面MN 所夹的锐角分别为和，大灯A与地面离地面的距离为‎1m则该车大灯照亮地面的宽度BC是 m .（不考虑其它因素）‎ 第16题图 ‎【答案】1.4‎ ‎9. （2011重庆市潼南,16,4分）如图，某小岛受到了污染，污染范围可 以大致看成是以点O为圆心，AD长为直径的圆形区域，为了测量受污染的圆形 区域的直径,在对应⊙O的切线BD（点D为切点）上选择相距‎3‎‎00米的B、C两点，分别测得∠ABD= 30°，∠ACD= 60°，则直径AD= 米.（结果精确到‎1米）‎ ‎（参考数据： ）‎ ‎【答案】260‎ 三、解答题 ‎1. （2011浙江金华，19，6分）生活经验表明，靠墙摆放的梯子，当50°≤α≤70°（α为梯子与地面所成的角），能够使人安全攀爬，现在有一长为‎6米的梯子AB，试求能够使人安全攀爬时，梯子的顶端能达到的最大高度AC.（结果保留两个有效数字，sin70°≈0.94，sin50°≈0.77，cos70°≈0.34，cos50°≈0.64）‎ ‎【解】由题意知，当α越大，梯子的顶端达到的最大高度越大.因为当50°≤α≤70°时，能够使人安全攀爬，所以当α=70°时AC最大.‎ 在Rt△ABC中，AB=6米，α=70°，‎ sin70°=，即0.94≈，解得AC ≈5.6.‎ 答：梯子的顶端能达到的最大高度AC≈5.6米.‎ ‎2. （2011安徽，19，10分）如图，某高速公路建设中需要确定隧道AB的长度．已知在离地面‎1500m高度C处的飞机上，测量人员测得正前方A、B两点处的俯角分别为60°和45°．求隧道AB的长．‎ ‎（参考数据：=1.73）‎ ‎【答案】∵OA， OB=OC=1500，‎ ‎ ∴AB=（m）.‎ ‎ 答：隧道AB的长约为‎635m．‎ ‎3. （2011广东东莞，17，7分）如图，小明家在A处，门前有一口池塘，隔着池塘有一条公路l，AB是A到l的小路。现新修一条路AC到公路l．小明测量出∠ACD=30°,∠ABD=45°,BC=‎50m．请你帮小明计算他家到公路l的距离AD的长度（精确到‎0.1m；参考数据：）‎ ‎【解】设小明家到公路的距离AD的长度为xm.‎ 在Rt△ABD中，‎ ‎∵∠ABD=，∴BD=AD=x 在Rt△ABD中，‎ ‎∵∠ACD=，∴，即 解得 小明家到公路的距离AD的长度约为68.2m. ……………………………………………8分 ‎4. （2011江苏扬州，25,10分）如图是某品牌太阳能热水器的实物图和横断面示意图，已知真空集热管AB与支架CD所在直线相交于水箱横断面⊙O的圆心，支架CD与水平面AE垂直，AB=150厘米，∠BAC=30°，另一根辅助支架DE=76厘米，∠CED=60°.‎ ‎(1)求垂直支架CD的长度。（结果保留根号）‎ ‎（2）求水箱半径OD的长度。（结果保留三个有效数字，参考数据：，）‎ ‎ ‎ ‎【答案】解：（1）在Rt△DCE中，∠CED=60°，DE=76，‎ ‎ ∵sin∠CED= ∴DC=DE×sin∠CED = 38 (厘米)‎ 答：垂直支架CD的长度为38厘米。‎ ‎ （2）设水箱半径OD=x厘米，则OC=(38+x)厘米，AO=(150+x)厘米，‎ ‎∵Rt△OAC中，∠BAC=30°‎ ‎∴AO=2×OC 即：150+x=2(38+x)‎ 解得：x=150－76≈18.52≈18.5(厘米)‎ 答：水箱半径OD的长度为18.5厘米。‎ ‎5. （2011山东德州20,10分）某兴趣小组用高为‎1.2米的仪器测量建筑物CD的高度．如示意图，由距CD一定距离的A处用仪器观察建筑物顶部D的仰角为，在A和C之间选一点B，由B处用仪器观察建筑物顶部D的仰角为．测得A，B之间的距离为‎4米，，，试求建筑物CD的高度．‎ A C D B E F G ‎【答案】解：设建筑物CD与EF的延长线交于点G，DG=x米． …………1分 在△中,，即． …………2分 A C D B E F G 在△中，，即． …………3分 ‎∴，．‎ ‎∴ ． ………5分 ‎∴． ………6分 解方程得：=19.2． ………8分 ‎∴ ． ‎ 答：建筑物高为20.4米． ………10分 ‎6. （2011山东威海，23，10分）一副直角三角板如图放置，点C在FD的延长线上，AB∥CF，∠F=∠ACB=90°, ∠E=45°,∠A=60°,AC=10,试求CD的长．‎ ‎【答案】 解：过点B作BM⊥FD于点M．‎ 在△ACB中，∠ACB=90°, ∠A=60°,AC=10,‎ ‎∴∠ABC=30°, BC=AC tan60°=10,‎ ‎∵AB∥CF，∴∠BCM=30°．‎ ‎∴‎ 在△EFD中，∠F=90°, ∠E=45°,‎ ‎∴∠EDF=45°,‎ ‎∴．‎ ‎∴．‎ ‎7. （2011山东烟台，21,8分）综合实践课上，小明所在小组要测量护城河的宽度。如图所示是护城河的一段，两岸ABCD，河岸AB上有一排大树，相邻两棵大树之间的距离均为‎10米.小明先用测角仪在河岸CD的M处测得∠α=36°，然后沿河岸走‎50米到达N点，测得∠β=72°。请你根据这些数据帮小明他们算出河宽FR（结果保留两位有效数字）.‎ ‎（参考数据：sin 36°≈0.59，cos 36°≈0.81，tan36°≈0.73，sin 72°≈0.95，cos 72°≈0.31，tan72°≈3.08） ‎ ‎ ‎ A B C D E F M N R α β ‎【答案】解：过点F作FG∥EM交CD于G.‎ 则MG＝EF＝‎20米. ‎ ‎∠FGN＝∠α＝36°.‎ ‎∴∠GFN＝∠β－∠FGN＝72°－36°＝36°.‎ ‎∴∠FGN＝∠GFN，‎ ‎∴FN＝GN＝50－20＝30（米）.‎ 在Rt△FNR中，‎ FR＝FN×sinβ＝30×sin72°＝30×0.95≈29（米）.‎ ‎8. (2011浙江绍兴，20，8分)为倡导“地摊生活”，常选择以自行车作为代步工具，如图1所示是一辆自行车的实物图，车架档与的长分别为‎45cm，‎60cm，且它们相互垂直，座杆的长为‎20cm，点在同一条直线上，且，如图2.‎ 第20题图2‎ ‎ ‎ ‎（1）求车架档的长 ‎（2）求车座点到车架档的距离. ‎ ‎（记过精确到1cm，参考数据：）‎ ‎【答案】解（1）‎ ‎=‎‎75 cm 车档架的长为‎75 cm ‎（2）过点作，垂足为点，‎ 距离 车座点到车档架的距离是‎63cm ‎9. （2011浙江省，21，10分）图1为已建设封顶的16层楼房和其塔吊图，图2为其示意图，吊臂AB与地面EH平行，测得A点到楼顶D的距离为‎5m，每层楼高‎3.5m，AE、BF、CH都垂直于地面．‎ ‎(1)求16层楼房DE的高度；‎ ‎(2)若EF=‎16m，求塔吊的高CH 的长（精确到‎0.1m）.‎ ‎【答案】据题意得：DE=3.5×16=56，AB=EF=16‎ ‎∵∠ACB=∠CBG－∠CAB=15°，‎ ‎∴∠ACB ＝∠CAB ‎∴CB=AB=16. ∴CG=BC×sin30°= 8‎ CH=CG+HG=CG+DE+AD=8+56+5=69.‎ ‎∴塔吊的高CH的长为‎69m.‎ ‎10．（2011浙江台州，21,10分）丁丁要制作一个形如图1的风筝，想在一个矩形材料中裁剪出如图2 阴影所示的梯形翅膀，请你根据图2中的数据帮助丁丁计算出BE，CD的长度（精确到个位，）‎ ‎ ‎ ‎【答案】解：在Rt△BEC中，∠BCE=30º,EC=51，∴BE=≈30，AE=64‎ ‎ 在Rt△AFD中，∠FAD=45º,FD=FA=51，∴CD=64—51≈13‎ ‎ ∴CD=‎13cm，BE=‎30cm.‎ ‎11. （2011浙江丽水，19，6分）生活经验表明，靠墙摆放的梯子，当50°≤α≤70°(α为梯子与地面所成的角)，能够使人安全攀爬，现在有一长为‎6米的梯子AB，试求能够使人安全攀爬时，梯子的顶端能达到的最大高度AC.(结果保留两个有效数字，sin70°≈0.94，sin50°≈0.77，cos70°≈0.34，cos50°≈0.64)‎ ‎【解】当α=70°时，梯子顶端达到的最大高度，‎ ‎∵sinα=，‎ ‎∴AC = sin70°×6≈0.94×6=5.64≈5.6(米)‎ 答：人安全攀爬梯子时，梯子的顶端达到的最大高度约‎5.6米.‎ ‎12. （2011江西，22，9分）图甲是一个水桶模型示意图，水桶提手结构的平面图是轴对称图形。当点O到BC（或DE）的距离大于或等于⊙O的半径时（⊙O是桶口所在圆，半径为OA），提手才能从图甲的位置转到图乙的位置，这样的提手才合格，现在用金属材料做了一个水桶提手（如图丙A-B-C-D-E-F，C-D是弧CD，其余是线段），O是AF的中点，桶口直径AF=‎34cm，AB=FE=‎5cm,∠ABC=∠FED=149°。请通过计算判断这个水桶提手是否合格。‎ ‎（参考数据：≈17.72，tan73.6°≈3.40，sin75.4°≈0.97。）‎ ‎【答案】解：连结OB，过点O作OG⊥BC于点G.在Rt△ABO中，‎ AB=5，AO=17，∴tan∠ABO=,‎ ‎∴∠ABO=73.6°,‎ ‎∴∠GBO=∠ABC-∠ABO=149°-73.6°=75.4°‎ 又∵OB=≈17.72，‎ ‎∴在Rt△OBG中，OG=OB×sin∠GBO=17.72×0.97≈17.19＞17.‎ ‎∴水桶提手合格.‎ ‎13. （2011湖南常德，24，8分）‎ 青青草原上，灰太狼每天都想着如何抓羊，而且是屡败屡试，永不言弃.（如图7所示）一天，灰太狼在自家城堡顶部A处测得懒羊羊所在地B处的俯角为60°，然后下到城堡的C处，测得B处的俯角为30°.已知AC=‎40米，若灰太狼以‎5m/s的速度从城堡底部D处出发，几秒钟后能抓到懒羊羊？（结果精确到个位）‎ 图7‎ ‎【答案】解：在Rt△BCD中，‎ ‎∵∠BCD=90°－30°=60°‎ ‎∴,则 在Rt△ABD中，‎ ‎∵∠ABD=60°‎ ‎∴ ‎ 即 ‎∴‎ 故约7秒钟后灰太狼能抓到懒羊羊.‎ ‎14. （2011湖南邵阳，20，8分）崀山成功列入世界自然遗产名录后，景区管理部门决定在八角寨假设旅游索道设计人员为了计算索道AB（索道起点为山脚B处，终点为山顶A处）的长度，采取了如图（八）所示的测量方法。在B处测得山顶A的仰角为16°，查阅相关资料得山高AC=‎325米，求索道AB的长度。（结果精确到‎1米，参考数据sin16°≈0.28，cos16°≈0.96，tan16°≈0.29）‎ ‎【答案】解：AB=AC÷sin 16°= 325÷0.28≈1161米。‎ ‎15. （2011湖南益阳，18，8分）如图8,AE是位于公路边的电线杆，为了使拉线CDE不影响汽车的正常行驶，电力部门在公路的另一边竖立了一根水泥撑杆BD，用于撑起拉线．已知公路的宽AB为‎8米，电线杆AE的高为‎12米，水泥撑杆BD高 为‎6米，拉线CD与水平线AC的夹角为67.4°．求拉线CDE 的总长L（A、B、C三点在同一直线上，电线杆、水泥杆的大 小忽略不计）．‎ ‎(参考数据：，，)‎ E A D B C 图8‎ ‎【答案】解：⑴在Rt中，，‎ ‎（m）. ‎ ‎， ‎ ‎，，， ‎ ‎（m）. ‎ ‎（m）‎ ‎16. （2011江苏连云港，24，10分）如图，自来水厂A和村庄B在小河l的两侧，现要在A，B间铺设一条输水答道.为了搞好工程预算，需测算出A，B间的距离.一小船在点P处测得A在正北方向，B位于南偏东24.5º方向，前行‎1200m,到达点Q处，测得A位于北偏西49º方向，B位于南偏西41º方向.‎ ‎（1）线段BQ与PQ是否相等？请说明理由；‎ ‎（2）求A，B间的距离.‎ ‎（参考数据：cos41º≈0.75）‎ ‎【答案】(1)∵B位于P点南偏东24.5º方向,∴∠BPQ=65.5º,又∵B位于Q点南偏西41º方向, ∴∠PQB=49º, ∴∠PBQ=65.5º, ∴PQ=BQ(等角对等边),(2)∵点P处测得A 在正北方向,在Rt△APQ中,,∴AQ=1600,由(1)得PQ=BQ=1200，∵在点Q处，测得A位于北偏西49º方向，B位于南偏西41º方向，∴∠AQB=90º，在Rt△ABQ中，AB=（m）.‎ ‎17. ‎ ‎18. （2011江苏苏州，25,8分）如图，小明在大楼‎30米高（即PH=‎30米）得窗口P处进行观测，测得山坡上A处的俯角为15°，山脚B处得俯角为60°，已知该山坡的坡度i（即tan∠ABC）为1：，点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上，且PH⊥HC.‎ ‎（1）山坡坡角（即∠ABC）的度数等于________度；‎ ‎（2）求A、B两点间的距离（结果精确到0.1米，参考数据：≈1.732）.‎ ‎【答案】解：（1）30.‎ ‎（2）由题意得：∠PBH=60°，∠APB=45°.‎ ‎∵∠ABC=30°，∴∠APB=90°.‎ 在Rt△PHB中，PB==20，‎ 在Rt△PBA中，AB=PB=20≈34.6.‎ 答：A、B两点间的距离约34.6米.‎ ‎19. （2011江苏宿迁,23,10分）如图，为了测量某建筑物CD的高度，先在地面上用测角仪自A处测得建筑物顶部的仰角是30°，然后在水平地面上向建筑物前进了‎100m，此时自B处测得建筑物顶部的仰角是45°．已知测角仪的高度是‎1.5m，请你计算出该建筑物的高度．（取＝1.732，结果精确到‎1m）‎‎（第23题）‎ ‎【答案】‎ 解：设CE＝xm，则由题意可知BE＝xm，AE＝(x＋100)m．‎ ‎ 在Rt△AEC中，tan∠CAE＝，即tan30°＝‎ ‎∴，3x＝(x＋100)‎ 解得x＝50＋50＝136.6‎ ‎∴CD＝CE＋ED＝(136.6＋1.5)＝138.1≈138(m)‎ 答：该建筑物的高度约为138m．‎ ‎20．（2011江苏泰州，23，10分）一幢房屋的侧面外壁的形状如图所示，它由等腰三角形OCD和矩形ABCD组成，∠OCD=25°．外墙壁上用涂料涂成颜色相同的条纹，其中一块的形状是四边形EFGH，测得FG ∥EH，GH=‎2.6cm , ∠FGB=65°． ‎ ‎（1）求证：GF⊥OC；‎ ‎（2）求EF的长（结果精确到0.1m）．‎ ‎(参考数据：sin25°=cos65°≈0.42，cos25°=sin65°≈0.91)‎ ‎【答案】解：（1）设CD与FG交于点M，由CD∥AB，∠FGB=65°，可得∠FGC=65°，又∠OCD=25°，于是在△FGC中，可得∠CFM=90°，即GF⊥OC．‎ ‎（2）过点G作GN⊥HE，则GN=EF，在Rt△GHN中，‎ sin ∠EHG=,即GN=GH sin ∠EHG=2.6 sin 65°=2.6×0.91=2.366≈‎2.4cm.‎ ‎21. （2011广东汕头，17，7分）如图，小明家在A处，门前有一口池塘，隔着池塘有一条公路l，AB是A到l的小路。现新修一条路AC到公路l．小明测量出∠ACD=30°,∠ABD=45°,BC=‎50m．请你帮小明计算他家到公路l的距离AD的长度（精确到‎0.1m；参考数据：）‎ ‎【解】设小明家到公路的距离AD的长度为xm.‎ 在Rt△ABD中，‎ ‎∵∠ABD=，∴BD=AD=x 在Rt△ABD中，‎ ‎∵∠ACD=，∴，即 解得 小明家到公路的距离AD的长度约为68.2m.‎ ‎22. （2011山东聊城，21，8分）被誉为东昌三宝之首的铁塔，始建于北宋时期，是我市现存的最古老的建筑，铁塔由塔身和塔座两部分组成（如图①）．为了测得铁塔的高度，小莹利用自制的测角仪，在C点测得塔顶E的仰角为45°，在D点测得塔顶E的仰角为60°，已知测角仪AC的高为1．‎6米，CD的长为‎6米，CD所在的水平线CG⊥EF于点G（如图②），求铁塔EF的高（结果精确到0．‎1米）．‎ ‎【答案】设EG＝x米，在Rt△CEG中，∵∠ECG＝45°，∴∠CEG＝45°，∴∠ECG＝∠CEG，∴CG＝EG，＝x米，在Rt△DEG中，∠EDG＝60°，tan∠EDB＝，∴DG＝，∵CG－DG＝CD＝6， ∴＝6，解得x＝9＋，∴EF＝EG＋FG＝9＋＋16≈158，所以铁塔高约为‎158米 ‎23. （2011山东潍坊，19，9分）今年“五一”‎ 假期，某数学活动小组组织一次登山活动.他们从山脚下A点出发沿斜坡AB到达B点，再从B点沿斜坡BC到达山顶C点，路线如图所示.斜坡AB的长为‎1040米，斜坡BC的长为‎400米，在C点测得B点的俯角为30°,.已知A点海拔‎121米，C点海拔‎721米.‎ ‎（1）求B点的海拔；‎ ‎（2）求斜坡AB的坡度.‎ ‎【解】（1）如图所示，过点C作CF⊥AM，F为垂足，过点B作BE⊥AM，BD⊥CF，E、D为垂足.‎ ‎∵在C点测得B点的俯角为30°，‎ ‎∴∠CBD=30°，又∵BC=‎400米，‎ ‎∴CD=400×sin30°=400×=200（米）.‎ ‎∴B点的海拔为721－200=521（米）‎ ‎（2）∵BE=521－121=400（米），AB=‎1040米，‎ ‎∴（米）.‎ ‎∴AB的坡度，所以斜坡AB的坡度为1：2.4.‎ ‎24. （2011广东汕头，19，7分）如图，直角梯形纸片ABCD中，AD∥BC，∠A＝90°，∠C=30°．折叠纸片使BC经过点D．点C落在点E处，BF是折痕，且BF= CF =8．‎ ‎（l）求∠BDF的度数；‎ ‎（2）求AB的长．‎ ‎【解】（1）∵BF=CF，∠C=，‎ ‎∴∠FBC=，∠BFC=‎ 又由折叠可知∠DBF=‎ ‎∴∠BDF=‎ ‎（2）在Rt△BDF中，‎ ‎∵∠DBF=，BF=8‎ ‎∴BD=‎ ‎∵AD∥BC，∠A=‎ ‎∴∠ABC=‎ 又∵∠FBC=∠DBF=‎ ‎∴∠ABD=‎ 在Rt△BDA中，‎ ‎∵∠AVD=，BD=‎ ‎∴AB=6．‎ ‎25. （2011四川广安，26，9分）某校初三课外活动小组，在测量树高的一次活动中，如图7所示，测得树底部中心A到斜坡底C的水平距离为8. ‎8m．在阳光下某一时刻测得‎1米的标杆影长为‎0.8m，树影落在斜坡上的部分CD= ‎3.2m．已知斜坡CD的坡比i=1：，求树高AB。（结果保留整数，参考数据：1.7）‎ ‎_‎ D ‎_‎ C ‎_‎ B ‎_‎ A i=1：‎ 图7‎ ‎【答案】解：如图，延长BD与AC的延长线交于点E，过点D作DHAE于H ‎∵CD=3.2 ∴DH=1.6 CH=‎ ‎∵ ∴HE=1.28‎ ‎∵ ∴AB=16‎ ‎_‎ D ‎_‎ C ‎_‎ B ‎_‎ A i=1：‎ ‎_‎ H ‎_‎ E ‎26. （2011四川内江，20，9分）放风筝是大家喜爱的一种运动。星期天的上午小明在大洲广场上放风筝。如图他在A处时不小心让风筝挂在了一棵树的树梢上，风筝固定在了D处，此时风筝线AD与水平线的夹角为30°。为了便于观察，小明迅速向前边移动边收线到达了离A处‎7米的B处，此时风筝线BD与水平线的夹角为45°。已知点A、B、C在同一条直线上，∠ACD=90°。请你求出小明此时所收回的风筝线的长度是多少米？（本题中风筝线均视为线段，，，最后结果精确到‎1米）‎ ‎【答案】设BC=CD=x米，得 ‎，解得 ‎∴AD－BD=2x－=(米)‎ ‎27. （2011四川宜宾,22,7分）如图，飞机沿水平方向（A，B两点所在直线）飞行，前方有一座高山，为了避免飞机飞行过低，就必须测量山顶M到飞行路线AB的距离MN．飞机能够测量的数据有俯角和飞行距离（因安全因素，飞机不能飞到山顶的正上方N处才测飞行距离），请设计一个求距离MN的方案，要求：‎ ‎（1）指出需要测量的数据（用字母表示，并在图中标出）；‎ ‎（2）用测出的数据写出求距离MN的步骤．‎ ‎（22题图）‎ ‎【答案】解：此题为开放题，答案不惟一，只要方案设计合理，可参照给分 ‎⑴如图，测出飞机在A处对山顶的俯角为，测出飞机在B处对山顶的俯角为，测出AB的距离为d，连接AM，BM．‎ ‎⑵第一步，在中， ∴‎ 第二步，在中， ∴‎ 其中，解得．‎ ‎（第25题解答图）‎ ‎28. (2011重庆綦江，20，6分)如图，小刚同学在綦江南州广场上观测新华书店楼房墙上的电子屏幕CD, 点A是小刚的眼睛，测得屏幕下端D处的仰角为30°，然后他正对屏幕方向前进了‎6米到达B处，又测得该屏幕上端C处的仰角为45°，延长AB与楼房垂直相交于点E,测得BE＝‎21米，请你帮小刚求出该屏幕上端与下端之间的距离CD. （结果保留根号）‎ ‎【答案】：解：∵∠CBE＝45° CE⊥AE ‎ ‎∴CE＝BE＝21 ‎ ‎ AE＝21＋6＝27 ‎ 在Rt△ADE中，∠DAE＝30°‎ ‎∴DE＝AE×tan30°＝27×＝9 ‎ ‎∴CD＝CE－DE＝21－9‎ ‎∴该屏幕上端与下端之间的距离CD＝21－9 (米).‎ ‎29. （2011江西南昌，22，9分）图甲是一个水桶模型示意图，水桶提手结构的平面图是轴对称图形。当点O到BC（或DE）的距离大于或等于⊙O的半径时（⊙O是桶口所在圆，半径为OA），提手才能从图甲的位置转到图乙的位置，这样的提手才合格，现在用金属材料做了一个水桶提手（如图丙A-B-C-D-E-F，C-D是弧CD，其余是线段），O是AF的中点，桶口直径AF=‎34cm，AB=FE=‎5cm,∠ABC=∠FED=149°。请通过计算判断这个水桶提手是否合格。‎ ‎（参考数据：≈17.72，tan73.6°≈3.40，sin75.4°≈0.97。）‎ 图甲 图乙 图丙 ‎【答案】解：连结OB，过点O作OG⊥BC于点G.在Rt△ABO中，‎ AB=5，AO=17，∴tan∠ABO=,‎ ‎∴∠ABO=73.6°,‎ ‎∴∠GBO=∠ABC-∠ABO=149°-73.6°=75.4°‎ 又∵OB=≈17.72，‎ ‎∴在Rt△OBG中，OG=OB×sin∠GBO=17.72×0.97≈17.19＞17.‎ ‎∴水桶提手合格.‎ ‎30. （2011安徽芜湖，18，8分）如图，某校数学兴趣小组的同学欲测量一座垂直于地面的古塔BD的高度，他们先在A处测得古塔顶端点的仰角为，再沿着的方向后退‎20m至处，测得古塔顶端点的仰角为.求该古塔BD的高度(,结果保留一位小数).‎ ‎【答案】‎ 解：根据题意可知: ‎ 在中,由得. …………………………2分 在中,由.得………………………4分 又∵,∴.∴(m).………………7分 答：该古塔的高度约为‎27.3m. ‎ ‎31. （2011山东济宁，18， 5分）日本福岛出现核电站事故后，我国国家海洋局高度关注事态发展，紧急调集海上巡逻的海检船，在相关海域进行现场检测与海水采样，针对核泄漏在极端情况下对海洋的影响及时开展分析评估．如图上午9时,海检船位于A处，观测到某港口城市P位于海检船的北偏西67.5°，海检船以21海里/时的速度向正北方向行驶，下午2时海检船到达B处，这时观测到城市P位于海检船的南偏西36.9°方向，求此时海检船所在B处与城市P的距离？（参考数据：sin36.9°≈，tan36.9°≈，sin67.5°≈，tan67.5°≈）‎ 第18题 ‎【答案】解：过点P作PC⊥AB，垂足为C，设PC=x海里．‎ ‎　　　　在Rt△APC中，∵tan∠A=，∴AC=．…………2分 ‎　　　　在Rt△PCB中，∵tan∠B=，∴BC=．…………4分 ‎ ∵AC＋BC=AB=21×5，∴，解得．‎ ‎　　　　∵，∴（海里）．‎ ‎　　　　∴海检船所在B处与城市P的距离为‎100海里．………………6分 ‎32. （2011四川成都，16,6分）如图，在亚丁湾一海域执行护航任务的我海军某军舰由东向西行驶．在航行到B处时，发现灯塔A在我军舰的正北方向‎500米处；当该军舰从B处向正西方向行驶至达C处时，发现灯塔A在我军舰的北偏东60°的方向.求该军舰行驶的路程．（计算过程和结果均不取近似值)‎ ‎【答案】解：由题意可知，在Rt△ABC中，AB=500，∠ACB=90°－60°=30°， ‎ ‎∵∠ACB=,‎ ‎∴BC=（），‎ ‎∴该军舰行驶的路程为米.‎ ‎33. （2011广东省，17，7分）如图，小明家在A处，门前有一口池塘，隔着池塘有一条公路l，AB是A到l的小路。现新修一条路AC到公路l．小明测量出∠ACD=30°,∠ABD=45°,BC=‎50m．请你帮小明计算他家到公路l的距离AD的长度（精确到‎0.1m；参考数据：）‎ ‎【解】设小明家到公路的距离AD的长度为xm.‎ 在Rt△ABD中，‎ ‎∵∠ABD=，∴BD=AD=x 在Rt△ABD中，‎ ‎∵∠ACD=，∴，即 解得 小明家到公路的距离AD的长度约为68.2m.‎ ‎34. （2011广东省，19，7分）如图，直角梯形纸片ABCD中，AD∥BC，∠A＝90°，∠C=30°．折叠纸片使BC经过点D．点C落在点E处，BF是折痕，且BF= CF =8．‎ ‎（l）求∠BDF的度数；‎ ‎（2）求AB的长．‎ ‎【解】（1）∵BF=CF，∠C=，‎ ‎∴∠FBC=，∠BFC=‎ 又由折叠可知∠DBF=‎ ‎∴∠BDF=‎ ‎（2）在Rt△BDF中，‎ ‎∵∠DBF=，BF=8‎ ‎∴BD=‎ ‎∵AD∥BC，∠A=‎ ‎∴∠ABC=‎ 又∵∠FBC=∠DBF=‎ ‎∴∠ABD=‎ 在Rt△BDA中，‎ ‎∵∠AVD=，BD=‎ ‎∴AB=6．‎ ‎35.‎ ‎ （2011江苏淮安，23，10分）题23-1图为平地上一幢建筑物与铁塔图，题23-2图为其示意图.建筑物AB与铁塔CD都垂直于底面，BD=‎30m，在A点测得D点的俯角为45°，测得C点的仰角为60°.求铁塔CD的高度.‎ ‎ ‎ 题23-1图 题23-2图 ‎【答案】解：如图，设过点A的水平线与CD交于点E，由题意得 ‎∠AEC=∠AED=90°，∠CAE=60°，∠DAE=45°，AE=BD=‎30m，‎ ‎∴CD=CE+DE=AE·tan60°+AE·tan45°=30+30(m).‎ ‎ 答：铁塔CD的高度为(30+30)m.‎ ‎36. ．(2011江苏南京，25，7分)如图，某数学课外活动小组测量电视塔AB的高度，他们借助一个高度为‎30m的建筑物CD进行测量，在点C处塔顶B的仰角为45°，在点E处测得B的仰角为37°（B、D、E三点在一条直线上）．求电视塔的高度h．‎ ‎（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）‎ A B E C D h ‎37°‎ ‎45°‎ ‎(第25题)‎ ‎【答案】解：在中，＝．‎ ‎∴EC＝≈（）．‎ 在中，∠BCA＝45°，∴‎ 在中，＝．∴．∴（）． ‎ 答：电视塔高度约为120．‎ ‎37. （2011四川凉山州，23，8分）在一次课题设计活动中，小明对修建一座‎87m长的水库大坝提出了以下方案；大坝的横截面为等腰梯形，如图，∥，坝高‎10m，迎水坡面的坡度，老师看后，从力学的角度对此方案提出了建议，小明决定在原方案的基础上，将迎水坡面的坡度进行修改，修改后的迎水坡面的坡度。‎ （1） 求原方案中此大坝迎水坡的长（结果保留根号）‎ （2） 如果方案修改前后，修建大坝所需土石方总体积不变，在方案修改后，若坝顶沿方向拓宽‎2.7m，求坝顶将会沿方向加宽多少米？‎ A B C E D ‎23题图 ‎【答案】‎ 解：⑴过点作于。 ‎ ‎ 在中，∵，且。‎ ‎ ∴， ‎ ‎ ⑵过点作于。‎ ‎ 在中，∵，且。‎ ‎ ∴， ‎ A B C M D G F E N ‎ 如图，延长至点，至点，‎ 连接，‎ ‎∵方案修改前后，修建大坝所需土石方 总体积不变。‎ ‎ ‎ ‎。‎ 即 。‎ ‎。 ‎ ‎ 答：坝底将会沿方向加宽。‎ ‎38. （2011江苏无锡，24，9分）(本题满分9分)如图，一架飞机由A向B沿水平直线方向飞行，在航线AB的正下方有两个山头C、D。飞机在A处时，测得山头C、D在飞机前方，俯角分别为60°和30°。飞机飞行了‎6千米到B处时，往后测得山头C的俯角为30°，而山头D恰好在飞机的正下方。求山头C、D之间的距离。‎ A B C D ‎【答案】‎ 解：在Rt△ABD中，∵∠BAD = 30°，∴BD = AB·tan30° = 6 × = 2．………………(2分)‎ ‎∵∠BAC = 60°，∠ABC = 30°，∴∠ACB = 90°，∴BC = AB·cos30° = 6 × = 3．‎ ‎…………(4分)‎ ‎ 过点C作CE⊥BD于点E，则∠CBE = 60°，CE = BC·sin60° = ．…………(6分)‎ ‎∴BE = BC·cos60° = ，………………………………(7分)‎ DE = BD − BE = 2 − = ．‎ ‎∴在Rt△CDE中，CD = = = (km)．‎ 答：山头C、D之间的距离为(km)．…………………………………………………(9分)‎ ‎39. （2011湖北黄冈，21，8分）如图，防洪大堤的横断面是梯形，背水坡AB的坡比 ‎（指坡面的铅直高度与水平宽度的比）．且AB=‎20 m．身高为‎1.7 m的小明站在大堤A点，测得高压电线杆端点D的仰角为30°．已知地面CB宽‎30 m，求高压电线杆CD的高度（结果保留三个有效数字，1.732）.‎ C D N M A B ‎ 第21题图 ‎【答案】 ≈36.0‎ ‎40. （2011湖北黄石，22，8分）东方山是鄂东南地区的佛教胜地，月亮山是黄荆山脉第二高峰，山顶上有黄石电视塔，据黄石地理资料记载：东方山海拔‎453.20米，月亮山海拔‎442.00米。一飞机从东方山到月亮山方向水平飞行，在东方山山顶D的正上方A处测得月亮山山顶C的俯角为α，在月亮山山顶C的正上方B处测得东方山山顶D处的俯角为β，如图（7），已知tanα=0.15987，tanβ=0.15847，若飞机的飞行速度为‎180米/秒，则该飞机从A到B处需多少时间？（精确到0.1秒）‎ ‎【答案】解：设AB＝x米，根据题意得，‎ AD＝x·tanβ=0.15847x BC=x·tanα=0.15987x ‎0.15847x+453.20=0.15987x+442.00‎ 解之得，0.0014x=11.2‎ x=8000‎ t=‎ t=44.4‎ 答：该飞机从A到B处需44.4秒 ‎41. （2011贵州贵阳，20，10分）‎ 某过街天桥的设计图是梯形ABCD（如图所示），桥面DC与地面AB平行，DC=‎62米，AB=‎88米．左斜面AD与地面AB的夹角为23°，右斜面BC与地面AB的夹角为30°，立柱DE⊥AB于E，立柱CF⊥AB于F，求桥面DC与地面AB之间的距离．（精确到‎0.1米）‎ ‎（第20题图）‎ ‎【答案】解：在Rt△ADE中，∠A=23°，‎ ‎∴AE=．‎ 在Rt△BCF中，∠B=30°，‎ ‎∴BF=．‎ ‎∵DE⊥AB，CF⊥AB，AB∥CD，‎ ‎∴CD=EF，DE=CF，‎ ‎∴++62=88．‎ 解得，DE≈6.4．‎ 即桥面DC与地面AB之间的距离约为‎6.4米．‎ ‎42. （2011江苏盐城，24，10分）如图，放置在水平桌面上的台灯的灯臂AB长为‎40cm，灯罩BC长为‎30cm，底座厚度为‎2cm，灯臂与底座构成的∠BAD=60°. 使用发现，光线最佳时灯罩BC与水平线所成的角为30°，此时灯罩顶端C到桌面的高度CE是多少cm？‎ ‎（结果精确到‎0.1cm，参考数据：≈1.732）‎ ‎【答案】过点B作BF⊥CD于F，作BG⊥AD于G. ‎ 在Rt△BCF中，∠CBF=30°，∴CF=BC·sin30°= 30× =15. ‎ 在Rt△ABG中，∠BAG=60°，∴BG=AB·sin60°= 40× = 20. ‎ ‎∴CE=CF+FD+DE=15+20+2=17+20≈51.64≈51.6（cm）cm. ‎ 答：此时灯罩顶端C到桌面的高度CE约是‎51.6cm. ‎ ‎43. （2011广东中山，17,7分）如图，小明家在A处，门前有一口池塘，隔着池塘有一条公路l，AB是A到l的小路。现新修一条路AC到公路l．小明测量出∠ACD=30°,∠ABD=45°,BC=‎50m．请你帮小明计算他家到公路l的距离AD的长度（精确到‎0.1m；参考数据：）‎ ‎【解】设小明家到公路的距离AD的长度为xm.‎ 在Rt△ABD中，‎ ‎∵∠ABD=，∴BD=AD=x 在Rt△ABD中，‎ ‎∵∠ACD=，∴，即 解得 小明家到公路的距离AD的长度约为68.3m.‎ ‎44. （2011湖北鄂州，21，8分）如图，防洪大堤的横断面是梯形，背水坡AB的坡比（指坡面的铅直高度与水平宽度的比）．且AB=20 m．身高为‎1.7 m的小明站在大堤A点，测得高压电线杆端点D的仰角为30°．已知地面CB宽‎30 m，求高压电线杆CD的高度（结果保留三个有效数字，1.732）.‎ C D N M A B ‎ 第21题图 ‎【答案】 ≈36.0‎ ‎45. （2011广东湛江24,10分）五一期间，小红到美丽的世界地质公园光岩参加社会实践活动，在景点P处测得景点B位于南偏东方向，然后沿北偏东方向走‎100米到达景点A，此时测得景点B正好位于景点A的正南方向，求景点A与景点B之间的距离．（结果精确到‎0.1米）‎ ‎【答案】过P作，垂足为D，则,‎ 所以，且米，‎ 所以AD=50米，‎ 又，,所以DB=DP，而,‎ 所以米。‎ ‎46. （2011贵州安顺，21，8分）一次数学活动课上，老师带领学生去测一条南北流向的河宽，如图所示，某学生在河东岸点A处观测到河对岸水边有一点C，测得C在A北偏西31°的方向上，沿河岸向北前行‎40米到达B处，测得C在B北偏西45°的方向上，请你根据以上数据，求这条河的宽度．（参考数值：tan31°≈）‎ 第21题图 ‎【答案】过点C作CDAB于D ，‎ 第21题图 D 由题意，，设CD = BD = x米，则AD =AB+BD =（40+x ‎）米，‎ 在Rt中，tan=，则，解得x = 60（米）．‎ ‎47. （2011湖南湘潭市，19，6分）（本题满分6分）‎ 莲城中学九年级数学兴趣小组为测量校内旗杆高度，如图，在C点测得旗杆 顶端A的仰角为30°，向前走了‎6米到达D点，在D点测得旗杆顶端A的仰角 为60°(测角器的高度不计).‎ ‎⑴ AD＝_______米; ‎ ‎⑵ 求旗杆AB的高度（）.‎ ‎30°‎ ‎60°‎ A ‎6米 D C B ‎【答案】解：（1）6 ‎ ‎（2）在Rt△ABD中，(米)．‎ 所以旗杆AB的高度为‎5.19米．‎ ‎48. （2011湖北荆州，21，8分）（本题满分8分）某河道上有一个半圆形的拱桥，河两岸筑有拦水堤坝，其半圆形桥洞的横截面如图所示.已知上、下桥的坡面线ME、NF与半圆相切，上、下桥斜面的坡度i＝1：3.7，桥下水深OP＝‎5米，水面宽度CD＝‎24米.设半圆的圆心为O，直径AB在直角顶点M、N的连线上，求从M点上坡、过桥、下坡到N点的最短路径长.（参考数据：，，）‎ ‎【答案】 解：连结OD、OE、OF，由垂径定理知：PD＝ 1 2 CD＝12（m） 在Rt△OPD中，（m），‎ ‎∴OE＝OD＝‎13m ‎ ‎∵tan∠EMO=i= 1： 3.7 ， ≈ 1：3.7 ‎ ‎∴∠EMO＝15°‎ 由切线性质知∠OEM＝90°‎ ‎∴∠EOM=75° 同理得∠NOF＝75°‎ ‎∴∠EOF＝180°-75°×2＝30° 在Rt△OEM中，tan15°＝‎ ‎∴EM＝3.7×13＝48.1（m）‎ 又EF的弧长＝30π×13÷180 ＝6.5（m）‎ ‎∴48.1×2+6.5＝102.7（m）‎ 即从M点上坡、过桥、再下坡到N点的最短路径长为‎102.7米.‎ ‎49.‎ ‎50.‎