中考强化训练专题圆

中考强化训练专题圆

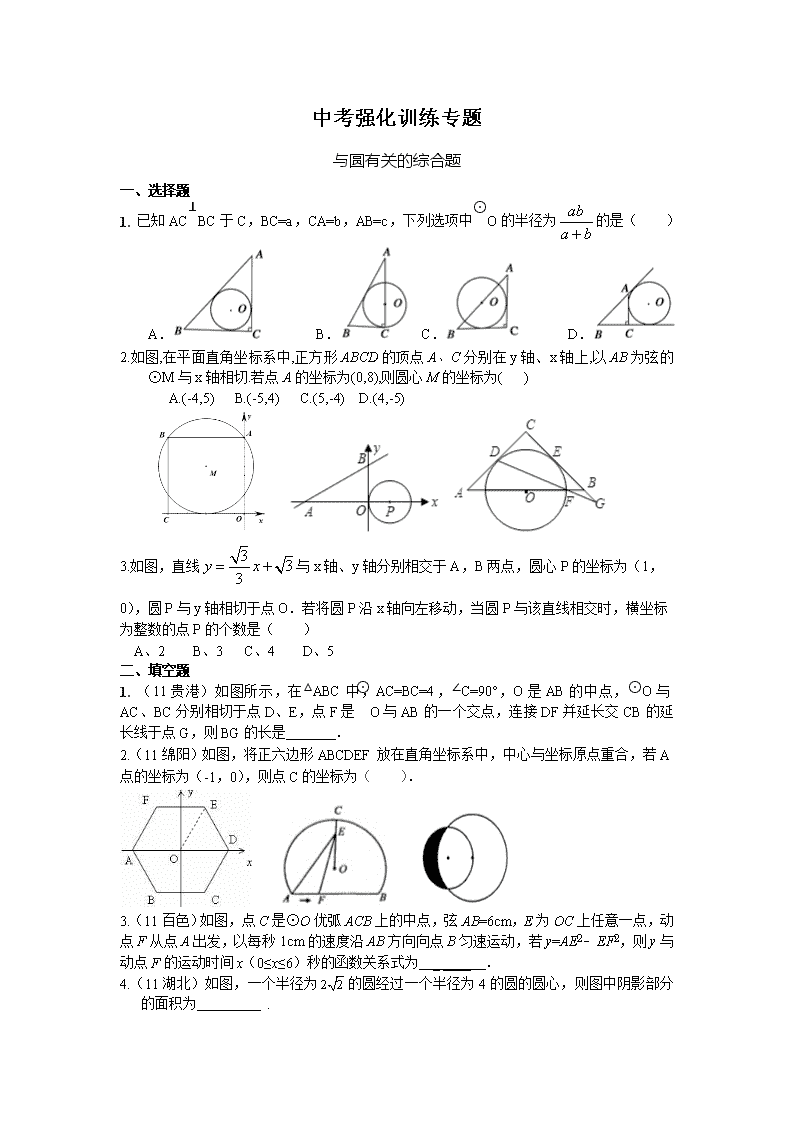
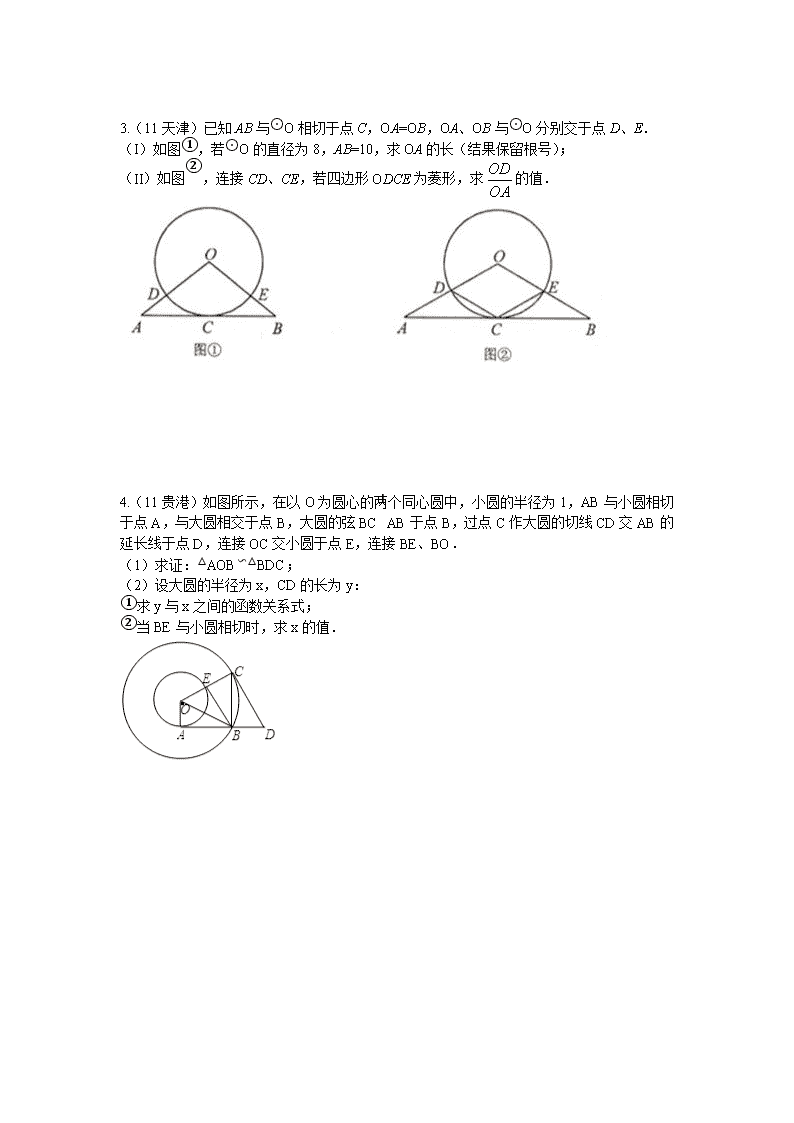
中考强化训练专题 与圆有关的综合题 一、选择题 ‎1. 已知AC⊥BC于C，BC=a，CA=b，AB=c，下列选项中⊙O的半径为的是（　　）‎ ‎ A． B． C． D．‎ ‎2.如图,在平面直角坐标系中,正方形ABCD的顶点A、C分别在y轴、x轴上,以AB为弦的⊙M与x轴相切.若点A的坐标为(0,8),则圆心M的坐标为( )‎ A.(-4,5) B.(-5,4) C.(5,-4) D.(4,-5)‎ ‎ ‎ ‎3.如图，直线与x轴、y轴分别相交于A，B两点，圆心P的坐标为（1，0），圆P与y轴相切于点O．若将圆P沿x轴向左移动，当圆P与该直线相交时，横坐标为整数的点P的个数是（　　）‎ A、2 B、‎3 C、4 D、5‎ 二、填空题 ‎1. （11贵港）如图所示，在△ABC中，AC=BC=4，∠C=90°，O是AB的中点，⊙O与AC、BC分别相切于点D、E，点F是⊙O与AB的一个交点，连接DF并延长交CB的延长线于点G，则BG的长是　 　．‎ ‎2.（11绵阳）如图，将正六边形ABCDEF放在直角坐标系中，中心与坐标原点重合，若A点的坐标为（-1，0），则点C的坐标为（ ）．‎ ‎ 3.（11百色）如图，点C是⊙O优弧ACB上的中点，弦AB=‎6cm，E为OC上任意一点，动点F从点A出发，以每秒‎1cm的速度沿AB方向向点B匀速运动，若y=AE2﹣EF2，则y与动点F的运动时间x（0≤x≤6）秒的函数关系式为　_ ____　．‎ ‎4.（11湖北）如图，一个半径为的圆经过一个半径为4的圆的圆心，则图中阴影部分的面积为 .‎ 三、解答题 ‎1. （11南京）如图，在Rt△ABC中，∠ACB=90°，AC=‎6cm，BC=‎8cm．P为BC的中点，动点Q从点P出发，沿射线PC方向以‎2cm/s的速度运动，以P为圆心，PQ长为半径作圆．设点Q运动的时间为t s．‎ ‎（1）当t=1.2时，判断直线AB与⊙P的位置关系，并说明理由；‎ ‎（2）已知⊙O为△ABC的外接圆．若⊙P与⊙O相切，求t的值．‎ ‎2.（11宿迁）如图，在平面直角坐标系中，O为坐标原点，P是反比例函数y＝（x＞0）图象上的任意一点，以P为圆心，PO为半径的圆与x、y轴分别交于点A、B．‎ ‎（1）判断P是否在线段AB上，并说明理由；‎ ‎（2）求△AOB的面积；‎ ‎（3）Q是反比例函数y＝（x＞0）图象上异于点P的另一点，请以Q为圆心，QO半径画圆与x、y轴分别交于点M、N，连接AN、MB．求证：AN∥MB．‎ ‎3.（11天津）已知AB与⊙O相切于点C，OA=OB，OA、OB与⊙O分别交于点D、E．‎ ‎（I）如图①，若⊙O的直径为8，AB=10，求OA的长（结果保留根号）；‎ ‎（II）如图②，连接CD、CE，若四边形ODCE为菱形，求的值．‎ ‎4.（11贵港）如图所示，在以O为圆心的两个同心圆中，小圆的半径为1，AB与小圆相切于点A，与大圆相交于点B，大圆的弦BC⊥AB于点B，过点C作大圆的切线CD交AB的延长线于点D，连接OC交小圆于点E，连接BE、BO．‎ ‎（1）求证：△AOB∽△BDC；‎ ‎（2）设大圆的半径为x，CD的长为y：‎ ‎①求y与x之间的函数关系式；‎ ‎②当BE与小圆相切时，求x的值．‎ ‎5.（11黔南）如图，点A，B，C，D在⊙O上，AB=AC，AD与BC相交于点E，AE=ED，延长DB到点F，使FB=BD，连接AF．‎ ‎（1）证明：△BDE∽△FDA；‎ ‎（2）试判断直线AF与⊙O的位置关系，并给出证明．‎ ‎6.如图，射线PG平分∠EPF，O为射线PG上一点，以O为圆心，10为半径作⊙O，分别与∠EPF两边相交于A、B和C、D，连结OA，此时有OA∥PE.‎ ‎（1）求证：AP＝AO；‎ ‎（2）若弦AB＝12，求tan∠OPB的值；‎ ‎（3）若以图中已标明的点（即P、A、B、C、D、O）构造四边形，则能构成菱形的四个点为 ，能构成等腰梯形的四个点为 或 或 .‎ ‎7．如图，直角坐标系中，已知两点O(0,0) A(2,0)，点B在第一象限且△OAB为正三角形，△OAB的外接圆交轴的正半轴于点C，过点C的圆的切线交X轴于点D．‎ ‎（1）求两点的坐标；‎ ‎（2）求直线的函数解析式；‎ ‎（3）设分别是线段上的两个动点，且平分四边形的周长．‎ 试探究：的最大面积？‎ ‎8．在平面直角坐标系中，已知直线经过点和点，直线的函数表达式为，与相交于点．是一个动圆，圆心在直线上运动，设圆心的横坐标是．过点作轴，垂足是点．‎ ‎⑴ 填空：直线的函数表达式是 ，交点的坐标是 ，的度数是 ；‎ ‎⑵ 当和直线相切时，请证明点到直线的距离等于的半径，并写出 时的值．‎ ‎⑶ 当和直线不相离时，已知的半径，记四边形的面积为(其中点是直线与的交点)．是否存在最大值？若存在，求出这个最大值及此时的值；若不存在，请说明理由．‎