初三中考数学试卷
初三中考数学试题
注意事项:
1.本试题分第Ⅰ卷和第Ⅱ卷两部分.第I卷4页为选择题,48分;第Ⅱ卷8页为非选择题,102分;全卷共12页,满分150分,考试时间为120分钟.
2.答第I卷前,考生务必将自己的姓名、考号、考试科目涂写在答题卡上,考试结束,试题和答题卡一并收回.
3.第I卷每题选出答案后,必须用2B铅笔把答题卡上对应题目的答案标号【ABCD】涂黑.如需改动,先用橡皮擦干净,再改涂其它答案.
4.考试时,允许使用科学计算器.
第Ⅰ卷(选择题共 48 分)
一、选择题:本大题共12小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得4分,选错、不选或选出的答案超过一个均记零分.
1.的绝对值是
(A)-2 (B) (C)2 (D)
2.下列计算正确的是
(A) (B)
(C) (D)
3.若反比例函数的图象经过点(-1 , 2 ),则这个函数的图象一定经过点
(A)(2,-1) (B)(,2) (C)(-2,-1) (D)(,2)
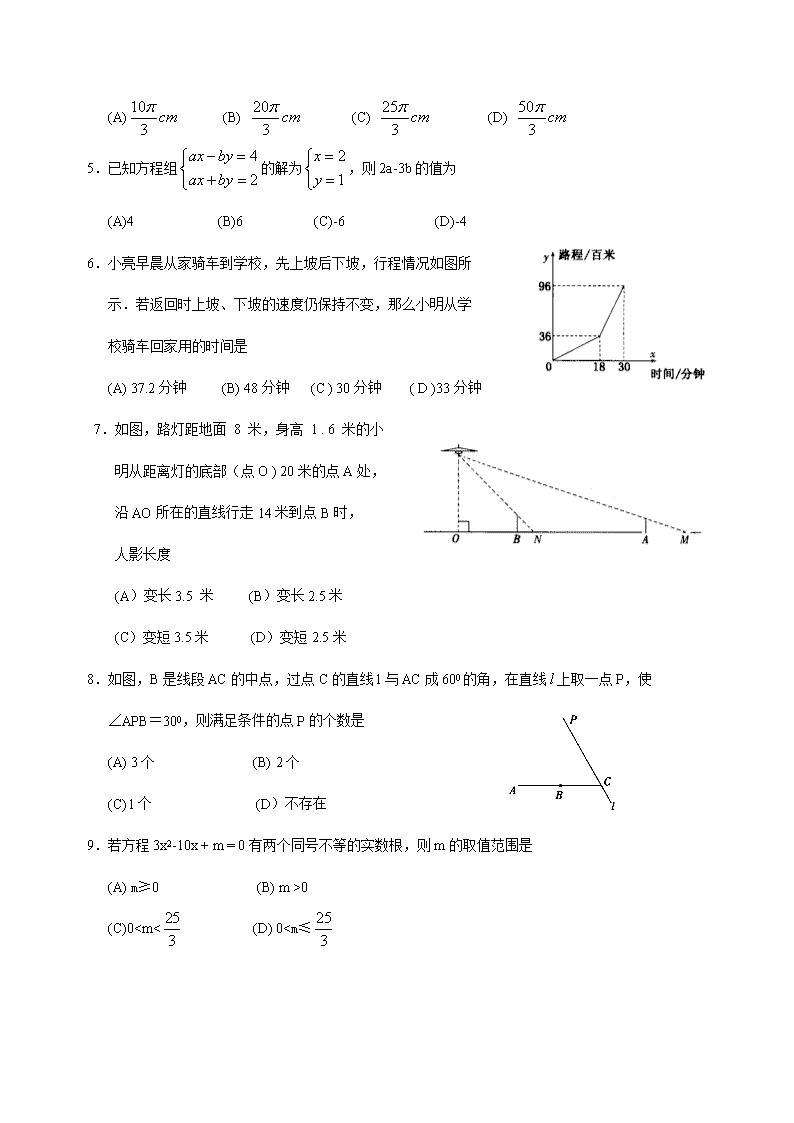
4.钟表的轴心到分针针端的长为5cm,那么经过40分钟,分针针端转过的弧长是
(A) (B) (C) (D)
5.已知方程组的解为,则2a-3b的值为
(A)4 (B)6 (C)-6 (D)-4
6.小亮早晨从家骑车到学校,先上坡后下坡,行程情况如图所
示.若返回时上坡、下坡的速度仍保持不变,那么小明从学
校骑车回家用的时间是
(A) 37.2分钟 (B) 48分钟 (C ) 30分钟 ( D )33分钟
7.如图,路灯距地面 8 米,身高 1 . 6 米的小
明从距离灯的底部(点O ) 20米的点A处,
沿AO所在的直线行走14米到点B时,
人影长度
(A)变长3.5 米 (B)变长2.5米
(C)变短3.5米 (D)变短2.5米
8.如图,B是线段AC的中点,过点C的直线l与AC成600的角,在直线上取一点P,使
∠APB=300,则满足条件的点P的个数是
(A) 3个 (B) 2个
(C) l个 (D)不存在
9.若方程3x2-10x + m = 0有两个同号不等的实数根,则m的取值范围是
(A) m≥0 (B) m >0
(C)0
76>72.67,所以候选人乙将被录用. ……………………………… 6分
(3)如果将笔试、面试、民主评议三项测试得分按4 : 3 : 3的比例确定个人成绩,那么
甲的个人成绩为:72.9(分),
乙的个人成绩为:77(分)
丙的个人成绩为: 77.4(分)
由于丙的个人成绩最高,所以候选人丙将被录用.…………………………… 10分
21.(本题满分12分)
解:设今年5月份汽油价格为x元/升,则去年5月份的汽油价格为(x-1.8)元/升.根据题
意,得……………………………………………………………… 5分
整理,得 x2 - l.8x - 14.4 = 0………………………………………………………………… 7分
解这个方程,得x1=4.8,x2=-3……………………………………………………………… 10分
经检验两根都为原方程的根,但x2=-3 不符合实际意义,故舍去.……………………11分
答:今年5月份的汽油价格为4.8元/升.……………………………………………… 12分
22.(本题满分12分)
解:△EMC是等腰直角三角形.………………………………………………… 2分
证明:由题意,得
DE=AC,∠DAE+∠BAC900.
∠DAB=900. ………………………………………………………………………… 3分
连接AM.∵DM=MB
∴MA=DB=DM,∠MDA=∠MAB=450.
∴∠MDE=∠MAC=1050
∴△EDM≌△CAM
∴EM=MC, ∠DME=∠AMC……………………………………………………… 8分
又∠EMC=∠EMA+∠AMC=∠EMA+∠DME=900
∴CM⊥EM…………………………………………………………………………… 11分
所以△EMC是等腰直角三角形 …………………………………………………… 12分
23.(本题满分12分)
解:(l)对于关于x的二次函数y =
由于△=(-m ) 2-4×l×=-m2-2<0,
所以此函数的图象与x轴没有交点……………………………………………… 1分
对于关于x的二次函数 y =.
由于△=(-m ) 2-4 ×l×=-m2-2<0,
所以此函数的图象与x轴没有交点
对于关于x的二次函数
由于
所以此函数的图象与x轴有两个不同的交点.
故图象经过A、B两点的二次函数为…………………3分
(2 )将A(-1,0)代入,得=0.
整理,得m2-2m = 0 .
解之,得m=0,或m = 2.…………………………………………………………5分
当m =0时,y=x2-1.令y = 0,得x2-1 = 0.
解这个方程,得x1=-1,x2=1
此时,B点的坐标是B (l, 0).………………………………………………………6分
当m=2时,y=x2-2x-3.令y=0,得x2-2x-3=0.
解这个方程,得x1=-1,x2=3
此时,B点的坐标是B(3,0). ……………………………………………………8分
(3) 当m =0时,二次函数为y=x2-1,此函数的图象开口向上,对称轴为x=0,所以当x<0时,函数值 y 随:的增大而减小.…………………………………………10分
当m=2时,二次函数为y = x2-2 x-3 = (x-1)2-4, 此函数的图象开口向上,对称轴为x = l,所以当x < l 时,函数值y随x的增大而减小.…………………………12分
24 .(本题满分12分)
解:(l)在△ABC中,AB=AC =1,∠BAC=300,
∴∠ABC=∠ACB=750,
∴∠ABD=∠ACE=1050, …………1分
∵∠DAE=1050.
∴∠DAB=∠CAE=750,
又∠DAB+∠ADB=∠ABC=750,
∴∠CAE=∠ADB…………………………………………………………3分
∴△ADB∽△EAC…………………………………………………………4分
∴
即……………………………………………………6分
(2)当α、β满足关系式时,函数关系式成立.………8分
理由如下:要使,即成立,须且只须△ADB∽△EAC.
由于∠ABD=∠ECA,故只须∠ADB=∠EAC. …………………………9分
又∠ADB+∠BAD=∠ABC=,
∠EAC+∠BAD=β-α, ……………………………………………………11分
所以只=β-α,须即.………………………………12分
25.(本题满分12分)港中数学网:www.gzsxw.net
解:( l)当点P与点C关于AB对称时,CP⊥AB,设垂足为D.
∵AB为⊙O的直径,
∴∠ACB=900.
∴AB=5,AC:CA=4:3,
∴BC=4, AC=3.
又∵AC·BC=AB·CD
∴ ……………………………………………2分
在Rt△ACB和Rt△PCQ中,
∠ACB=∠PCQ=900, ∠CAB=∠CPQ,
Rt△ACB∽Rt△PCQ
∴……4分
(2)当点P运动到弧AB的中点时,过点B作BE⊥PC
于点E(如图).
∵P是弧AB的中点,
∴…6分
又∠CPB=∠CAB
∴∠CPB= tan∠CAB=
∴而从……8分
由(l)得,………………………………………9分
(3)点P在弧AB上运动时,恒有
故PC最大时,CQ取到最大值.………………………………………11分
当PC过圆心O,即PC取最大值5时,CQ 最大值为……………12分