中考几何部分知识点总结

中考几何部分知识点总结

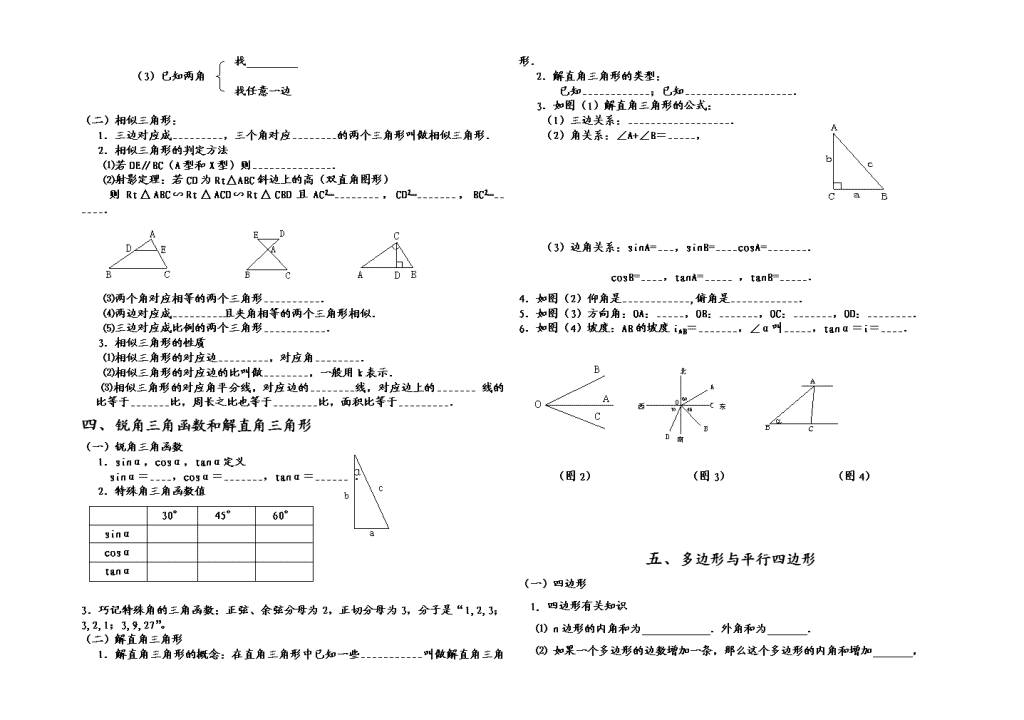
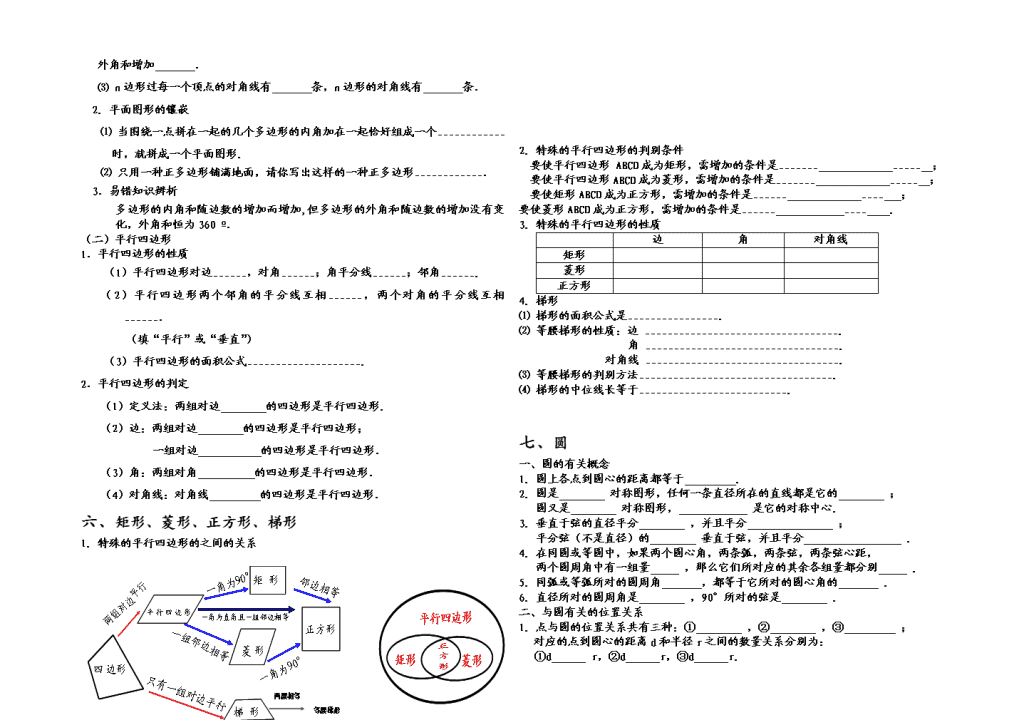
中考《几何部分》知识点总结 一、几何初步及平行线、相交线 ‎1.直线、线段的性质： 两点确定一条直线，即过两点有且只有一条直线；两点之间 最短。‎ ‎2.角： （1） 1周角＝_______，1平角＝_______,1直角＝_______．‎ ‎（2） 如果两个角的和 度，就说这两个角互余，同角或等角的余角相等；‎ 如果_____________________互为补角，__________________的补角相等.‎ ‎4.相交线：（1）对顶角： ______________________叫对顶角，对顶角___________.‎ ‎ （2）邻补角： 叫邻补角，邻补角 。‎ ‎ （3）垂线： 叫垂线。‎ ‎ 性质：平面内，过一点有且只有_____条直线与已知直线垂直.‎ ‎ 最短。‎ ‎ （4）同位角、内错角、同旁内角：（画图说明）‎ ‎5．平行线：（1）定义：‎ ‎(2)公理：过直线外一点有___________条直线与已知直线平行.‎ ‎(3)性质：两直线平行，_________相等，________相等，________互补.‎ ‎(4)判定：________相等,或______相等,或______互补，两直线平行.‎ ‎6.距离： （1）两点的距离： 。 ‎ ‎（2）点到直线的距离： 。 ‎ ‎（3）平行线间的距离： 。‎ ‎7．线段的垂直平分线：‎ ‎ 性质：线段垂直平分线上的到这条线段的 的距离相等；‎ ‎ 判定：到线段 的点在线段的垂直平分线上。‎ ‎8.角的平分线：‎ ‎ 性质：角平分线上的点到角 相等；‎ ‎ 判定：到角 的点在这个角的平分线上。‎ ‎ ‎ 二、三角形的有关性质 ‎（一）三角形的分类：‎ ‎1．三角形按角分为______________，______________，_____________．‎ ‎2．三角形按边分为_______________,__________________.‎ ‎（二）三角形的性质：‎ ‎1．三角形中任意两边之和____第三边，两边之差_____第三边 ‎2．三角形的内角和为_______，外角与内角的关系：__________________．‎ ‎（三）三角形中的主要线段：‎ ‎1．___________________________________叫三角形的中位线．‎ ‎2．中位线的性质：____________________________________________．‎ ‎3．三角形三条中位线将三角形分成四个面积相等的全等三角形。‎ ‎4．角平分线：三角形的角平分线交于一点，这点叫三角形的内心，它到三角形三边 的距离 ，内心也是三角形内切圆的圆 ‎5．三角形三边的垂直平分线：三角形三边的垂直平分线交于一点，这点叫做三角形的外心，它到三角形三个顶点的距离 ，外心也是三角形外接圆的圆心。‎ ‎6．三角形的中线、高线、角平分线都是____________．(线段、射线、直线)‎ ‎（四）等腰三角形的性质与判定：‎ ‎1. 等腰三角形的两底角__________；‎ ‎2. 等腰三角形底边上的______、底边上的________和顶角的_______互相重合（三线合一）；‎ ‎3. 有两个角相等的三角形是_________．‎ ‎（五）等边三角形的性质与判定：‎ ‎1. 等边三角形每个角都等于_______，同样具有“三线合一”的性质；‎ ‎2. 三个角相等的三角形是________，‎ 三边相等的三角形是_______，‎ 一个角等于60°的_______三角形是等边三角形．‎ ‎（六）直角三角形的性质与判定：‎ ‎1. 直角三角形两锐角________．‎ ‎2. 直角三角形中30°所对的直角边等于斜边的________．‎ ‎3. 直角三角形中，斜边的中线等于斜边的______．；‎ ‎4. 勾股定理：_________________________________________．‎ ‎5. 勾股定理的逆定理： 。‎ 三、全等三角形和相似三角形 ‎（一）全等三角形：‎ ‎1．全等三角形:____________、______________的三角形叫全等三角形.‎ ‎2. 三角形全等的判定方法有:_______、______、_______、______.直角三角形全等的判定除以上的方法还有________.‎ ‎3. 全等三角形的性质：全等三角形___________，____________.‎ ‎4. 全等三角形的面积_______、周长_____、对应高、______、_______相等.‎ ‎5．证明三角形全等的思路：‎ ‎ 找夹角 ‎（1）已知两边 找直角 ‎ 找 ‎ ‎ 边为角的对边时， 找 ‎ ‎ （2）已知一边一角 找夹角的另一边 ‎ 边为角的邻边时， 找夹边的 ‎ ‎ 找边的对角 ‎ 找 ‎ ‎ （3）已知两角 ‎ 找任意一边 ‎（二）相似三角形：‎ ‎1．三边对应成_________，三个角对应________的两个三角形叫做相似三角形．‎ ‎2．相似三角形的判定方法 ‎⑴若DE∥BC（A型和X型）则______________．‎ ‎⑵射影定理：若CD为Rt△ABC斜边上的高（双直角图形）‎ 则Rt△ABC∽Rt△ACD∽Rt△CBD且AC2=________，CD2=_______，BC2=__ ____．‎ ‎ ‎ ‎⑶两个角对应相等的两个三角形__________．‎ ‎⑷两边对应成_________且夹角相等的两个三角形相似．‎ ‎⑸三边对应成比例的两个三角形___________．‎ ‎3．相似三角形的性质 ‎⑴相似三角形的对应边_________，对应角________．‎ ‎⑵相似三角形的对应边的比叫做________，一般用k表示．‎ ‎⑶相似三角形的对应角平分线，对应边的________线，对应边上的_______线的比等于_______比，周长之比也等于________比，面积比等于_________． ‎ 四、锐角三角函数和解直角三角形 ‎（一）锐角三角函数 α a b c ‎1．sinα，cosα，tanα定义 sinα＝____，cosα＝_______，tanα＝______ ．‎ ‎2．特殊角三角函数值 ‎30°‎ ‎45°‎ ‎60°‎ sinα cosα tanα ‎3．巧记特殊角的三角函数：正弦、余弦分母为2，正切分母为3，分子是“1,2,3；3,2,1；3,9,‎27”‎。‎ ‎（二）解直角三角形 ‎1．解直角三角形的概念：在直角三角形中已知一些___________叫做解直角三角形．‎ ‎2．解直角三角形的类型：‎ 已知____________；已知___________________． ‎ ‎3．如图（1）解直角三角形的公式： ‎ ‎（1）三边关系：__________________． ‎ ‎（2）角关系：∠A+∠B＝_____， ‎ ‎ ‎ ‎（3）边角关系：sinA=___，sinB=____cosA=_______． ‎ cosB=____，tanA=_____ ，tanB=_____． ‎ ‎4．如图（2）仰角是____________,俯角是____________． ‎ ‎5．如图（3）方向角：OA：_____，OB：_______，OC：_______，OD：________．‎ ‎6．如图（4）坡度：AB的坡度iAB＝_______，∠α叫_____，tanα＝i＝____．‎ O A B C ‎ ‎ ‎（图2） （图3） （图4）‎ 五、多边形与平行四边形 ‎（一）四边形 ‎1. 四边形有关知识 ‎⑴ n边形的内角和为 ．外角和为 ．‎ ‎⑵ 如果一个多边形的边数增加一条，那么这个多边形的内角和增加 ，‎ 外角和增加 ．‎ ‎⑶ n边形过每一个顶点的对角线有 条，n边形的对角线有 条．‎ ‎2. 平面图形的镶嵌 ‎ ‎⑴ 当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个____________时，就拼成一个平面图形.‎ ‎⑵ 只用一种正多边形铺满地面，请你写出这样的一种正多边形____________．‎ ‎3．易错知识辨析 多边形的内角和随边数的增加而增加,但多边形的外角和随边数的增加没有变化，外角和恒为360 º．‎ ‎（二）平行四边形 ‎1．平行四边形的性质 ‎（1）平行四边形对边______，对角______；角平分线______；邻角______.‎ ‎（2）平行四边形两个邻角的平分线互相______，两个对角的平分线互相______．‎ ‎（填“平行”或“垂直”）‎ ‎（3）平行四边形的面积公式____________________.‎ ‎2．平行四边形的判定 ‎（1）定义法：两组对边 的四边形是平行四边形.‎ ‎（2）边：两组对边 的四边形是平行四边形；‎ 一组对边 的四边形是平行四边形．‎ ‎（3）角：两组对角 的四边形是平行四边形．‎ ‎（4）对角线：对角线 的四边形是平行四边形．‎ 六、矩形、菱形、正方形、梯形 ‎1. 特殊的平行四边形的之间的关系 ‎ ‎ ‎2. 特殊的平行四边形的判别条件 要使平行四边形 ABCD成为矩形，需增加的条件是_______ _____ ； ‎ 要使平行四边形ABCD成为菱形，需增加的条件是_______ _____ ；‎ 要使矩形ABCD成为正方形，需增加的条件是______ ____ ；‎ 要使菱形ABCD成为正方形，需增加的条件是______ ____ .‎ ‎3. 特殊的平行四边形的性质 边 角 对角线 矩形 菱形 正方形 ‎4. 梯形 ⑴ 梯形的面积公式是________________.‎ ⑵ 等腰梯形的性质：边 __________________________________.‎ 角 __________________________________.‎ 对角线 __________________________________.‎ ⑶ 等腰梯形的判别方法__________________________________.‎ ⑷ 梯形的中位线长等于__________________________.‎ 七、圆 一、圆的有关概念 ‎1. 圆上各点到圆心的距离都等于 .‎ ‎2. 圆是 对称图形，任何一条直径所在的直线都是它的 ；‎ 圆又是 对称图形， 是它的对称中心.‎ ‎3. 垂直于弦的直径平分 ，并且平分 ；‎ 平分弦（不是直径）的 垂直于弦，并且平分 .‎ ‎4. 在同圆或等圆中，如果两个圆心角，两条弧，两条弦，两条弦心距，‎ 两个圆周角中有一组量 ，那么它们所对应的其余各组量都分别 .‎ ‎5. 同弧或等弧所对的圆周角 ，都等于它所对的圆心角的 .‎ ‎6. 直径所对的圆周角是 ，90°所对的弦是 .‎ 二、与圆有关的位置关系 ‎1. 点与圆的位置关系共有三种：① ，② ，③ ；‎ 对应的点到圆心的距离d和半径r之间的数量关系分别为：‎ ‎①d r，②d r，③d r.‎ ‎2. 直线与圆的位置关系共有三种：① ，② ，③ .‎ 对应的圆心到直线的距离d和圆的半径r之间的数量关系分别为：‎ ‎①d r，②d r，③d r.‎ ‎3. 圆与圆的位置关系共有五种：① ，② ，③ ，④ ，⑤ ；‎ 两圆的圆心距d和两圆的半径R、r（R≥r）之间的数量关系分别为：①d R－r，‎ ‎②d R－r，③ R－r d R＋r，④d R＋r，⑤d R＋r.‎ ‎4. 圆的切线 过切点的半径；‎ 经过 的一端，并且 这条 的直线是圆的切线.‎ ‎5. 从圆外一点可以向圆引 条切线， 相等， 相等.‎ ‎6. 三角形的三个顶点确定 个圆，这个圆叫做三角形的外接圆，三角形的外接圆的圆心叫 心，是三角形 的交点，它到 相等。‎ ‎7. 与三角形各边都相切的圆叫做三角形的 ，内切圆的圆心是三角形 的交点，叫做三角形的 ，它到 相等.‎ 三、与圆有关的计算 ‎1. 圆的周长为 ，1°的圆心角所对的弧长为 ，‎ n°的圆心角所对的弧长为 ，弧长公式为 .‎ ‎2. 圆的面积为 ，1°的圆心角所在的扇形面积为 ，‎ n°的圆心角所在的扇形面积为S= = = .‎ ‎3. 圆柱的侧面积公式：S=.（其中为 的半径，为 的高）。‎ ‎4. 圆柱的全面积公式：S= + 。‎ ‎5. 圆锥的侧面积公式：S=.（其中为 的半径，为 的长）。‎ ‎6. 圆锥的全面积公式：S= + 。‎ 八、视图与投影 ‎1. 从 观察物体时，看到的图叫做主视图 ；从 观 察物体时，看到的图叫做左视图 ；从 观察物体时，看到的图叫做俯视图.‎ ‎2. 主视图与俯视图的 一致；主视图与左视图的 一致；俯视图与左视图的 ‎ 一致.‎ ‎3. 叫盲区.‎ ‎4. 投影可分为平行投影与中心投影.其中 所形成的投影叫平行投影；‎ ‎ 所形成的投影叫中心投影.‎ ‎5. 利用光线是否平行或是否交于一点来判断是 投影或 投影，以及光源的位置和物体阴影的位置.‎ 九、轴对称与中心对称 ‎1. 如果一个图形沿一条直线对折，对折后的两部分能 ，那么这个图形就是 ，这条直线就是它的 .‎ ‎2. 如果一个图形沿一条直线折叠，如果它能与另一个图形 ，那么这两个图形成 ，这条直线就是 ，折叠后重合的对应点就是 。‎ ‎3. 如果两个图形关于 对称，那么对称轴是任何一对对应点所连线段的 .‎ ‎4. 把一个图形绕着某一个点旋转 °，如果旋转后的图形能够与原来的图形 ，那么这个图形叫做 图形，这个点就是它的 ．‎ ‎5. 把一个图形绕着某一个点旋转 °，如果它能够与另一个图形 ，那么就说这两个图形关于这个点 ，这个点叫做 ．这两个图形中的对应点叫做关于中心的 ．‎ ‎6. 关于中心对称的两个图形，对称点所连线段都经过 ，而且被对称中心所 ．关于中心对称的两个图形是 图形.‎ ‎7. 两个点关于原点对称时，它们的坐标符号 ，即点关于原点的对称点为 .‎ 十、平移与旋转 ‎1. 一个图形沿着一定的方向平行移动一定的距离，这样的图形运动称为______，它是由移动的 和 所决定．‎ ‎2. 平移的特征是：经过平移后的图形与原图形的对应线段 ，对应 ，图形的 与 都没有发生变化，即平移前后的两个图形 ；且对应点所连的线段 ．‎ ‎3. 图形旋转的定义：把一个图形 的图形变换，叫做旋转， 叫做旋转中心， 叫做旋转角．‎ ‎4. 图形的旋转由 、 和 所决定．其中①旋转 在旋转过程中保持不动．②旋转 分为 时针和 时针. ③旋转 一般小于360º.‎ ‎5. 旋转的特征是：图形中每一点都绕着 旋转了 的角度，对应点到旋转中心的 相等，对应 相等，对应 相等，图形的 都没有发生变化.也就是旋转前后的两个图形 .‎