中考数学真题分类汇编套专题四十九判断说理型问题
解答题
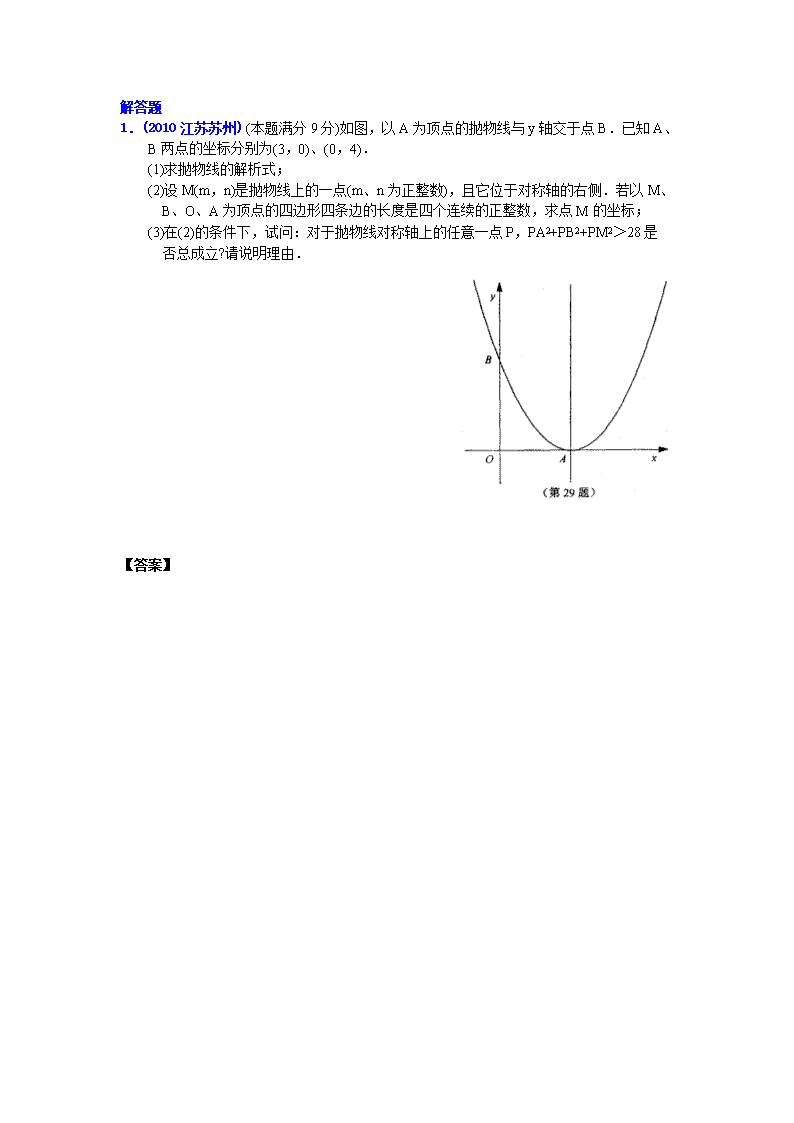
1.(2010江苏苏州) (本题满分9分)如图,以A为顶点的抛物线与y轴交于点B.已知A、B两点的坐标分别为(3,0)、(0,4).
(1)求抛物线的解析式;
(2)设M(m,n)是抛物线上的一点(m、n为正整数),且它位于对称轴的右侧.若以M、B、O、A为顶点的四边形四条边的长度是四个连续的正整数,求点M的坐标;
(3)在(2)的条件下,试问:对于抛物线对称轴上的任意一点P,PA2+PB2+PM2>28是
否总成立?请说明理由.
【答案】
2.(10湖南益阳)如图9,在平面直角坐标系中,已知A、B、C三点的坐标分别为A(-2,0),B(6,0),C(0,3).
(1)求经过A、B、C三点的抛物线的解析式;
(2)过C点作CD平行于轴交抛物线于点D,写出D点的坐标,并求AD、BC的交点E的坐标;
(3)若抛物线的顶点为P,连结PC、PD,判断四边形CEDP的形状,并说明理由.
【答案】
解:⑴ 由于抛物线经过点,可设抛物线的解析式为,则,
解得
∴抛物线的解析式为 ……………………………4分
⑵ 的坐标为 ……………………………5分
直线的解析式为
直线的解析式为
由
求得交点的坐标为 ……………………………8分
⑶ 连结交于,的坐标为
又∵,
∴,且
∴四边形是菱形 ……………………………12分
3.(2010辽宁丹东市)如图, 已知等边三角形ABC中,点D,E,F分别为边AB,AC,BC的中点,M为直线BC上一动点,△DMN为等边三角形(点M的位置改变时, △DMN也随之整体移动) .
(1)如图①,当点M在点B左侧时,请你判断EN与MF有怎样的数量关系?点F是否在直线NE上?都请直接写出结论,不必证明或说明理由;
(2)如图②,当点M在BC上时,其它条件不变,(1)的结论中EN与MF的数量关系是否仍然成立?若成立,请利用图②证明;若不成立,请说明理由;
(3)若点M在点C右侧时,请你在图③中画出相应的图形,并判断(1)的结论中EN
与MF的数量关系是否仍然成立?若成立?请直接写出结论,不必证明或说明理由.
图①
图②
图③
第25题图
A
·
B
C
D
E
F
·
·
·
【答案】(1)判断:EN与MF相等 (或EN=MF),点F在直线NE上, 3分
(说明:答对一个给2分)
(2)成立. 4分
证明:
法一:连结DE,DF. 5分
∵△ABC是等边三角形, ∴AB=AC=BC.
又∵D,E,F是三边的中点,
∴DE,DF,EF为三角形的中位线.∴DE=DF=EF,∠FDE=60°.
又∠MDF+∠FDN=60°, ∠NDE+∠FDN=60°,
∴∠MDF=∠NDE. 7分
在△DMF和△DNE中,DF=DE,DM=DN, ∠MDF=∠NDE,
∴△DMF≌△DNE. 8分
N
C
A
B
F
M
D
E
N
C
A
B
F
M
D
E
∴MF=NE. 9分
法二:
延长EN,则EN过点F. 5分
∵△ABC是等边三角形, ∴AB=AC=BC.
又∵D,E,F是三边的中点, ∴EF=DF=BF.
∵∠BDM+∠MDF=60°, ∠FDN+∠MDF=60°,
∴∠BDM=∠FDN. 7分
又∵DM=DN, ∠ABM=∠DFN=60°,
∴△DBM≌△DFN. 8分
∴BM=FN.
∵BF=EF, ∴MF=EN. 9分
法三:
连结DF,NF. 5分
∵△ABC是等边三角形,
∴AC=BC=AC.
又∵D,E,F是三边的中点,
∴DF为三角形的中位线,∴DF=AC=AB=DB.
又∠BDM+∠MDF=60°, ∠NDF+∠MDF=60°,
∴∠BDM=∠FDN. 7分
在△DBM和△DFN中,DF=DB,
DM=DN, ∠BDM=∠NDF,∴△DBM≌△DFN.
∴∠B=∠DFN=60°. 8分
又∵△DEF是△ABC各边中点所构成的三角形,
∴∠DFE=60°.
∴可得点N在EF上,
∴MF=EN. 9分
(3)画出图形(连出线段NE), 11分
MF与EN相等的结论仍然成立(或MF=NE成立). 12分
4.(2010山东日照)如图,小明在一次高尔夫球争霸赛中,从山坡下O点打出一球向球洞A点飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大水平高度12米时,球移动的水平距离为9米 .已知山坡OA与水平方向OC的夹角为30o,O、A两点相距8米.
(1)求出点A的坐标及直线OA的解析式;
(2)求出球的飞行路线所在抛物线的解析式;
(3)判断小明这一杆能否把高尔夫球从O点直接打入球洞A点 .
【答案】
23.(本题满分10分)
解:(1)在Rt△AOC中,
∵∠AOC=30 o ,OA=8,
∴AC=OA·sin30o=8×=,
OC=OA·cos30o=8×=12.
∴点A的坐标为(12,). …………………………………2分
设OA的解析式为y=kx,把点A(12,)的坐标代入得:
=12k ,
∴k= ,
∴OA的解析式为y=x; …………………… ……………………4分
(2) ∵顶点B的坐标是(9,12), 点O的坐标是(0,0)
∴设抛物线的解析式为y=a(x-9)+12,…………………………………6分
把点O的坐标代入得:
0=a(0-9)+12,解得a= ,
∴抛物线的解析式为y= (x-9)+12
及y= x+ x; …………………………………………………8分
(3) ∵当x=12时,y= ,
∴小明这一杆不能把高尔夫球从O点直接打入球洞A点. …………10分
5.(2010山东济宁)(第22题)
数学课上,李老师出示了这样一道题目:如图,正方形的边长为,为边延长线上的一点,为的中点,的垂直平分线交边于,交边的延长线于.当时,与的比值是多少?
经过思考,小明展示了一种正确的解题思路:过作直线平行于交,分别于,,如图,则可得:,因为,所以.可求出和的值,进而可求得与的比值.
(1) 请按照小明的思路写出求解过程.
(2) 小东又对此题作了进一步探究,得出了
的结论.你认为小东的这个结论正确吗?如果正确,请给予证明;如果不正确,请说明理由.
【答案】
(1)解:过作直线平行于交,分别于点,,
则,,.
∵,∴. 2分
∴,.
∴. 4分
(2)证明:作∥交于点, 5分
则,.
∵,
∴.
∵,,
∴.∴. 7分
∴. 8分(第22题)
6.(2010四川凉山)已知:抛物线,顶点,与轴交于A、B两点,。
(1) 求这条抛物线的解析式;
(2) 如图,以AB为直径作圆,与抛物线交于点D,与抛物线的对称轴交于点F,依次连接A、D、B、E,点Q为线段AB上一个动点(Q与A、B两点不重合),过点Q作于,于,请判断是否为定值;若是,请求出此定值,若不是,请说明理由;
(3) 在(2)的条件下,若点H是线段EQ上一点,过点H作,分别与边、相交于、,(与、不重合,与、
不重合),请判断是否成立;若成立,请给出证明,若不成立,请说明理由。
第26题图
A
B
x
G
F
M
H
E
N
Q
O
D
C
y
【答案】
7.(2010 嵊州市)(10分)已知:在四边形ABCD中,AD∥BC,∠BAC=∠D,点E、F分别在BC、CD上,且∠AEF=∠ACD,试探究AE与EF之间的数量关系。
(1)如图1,若AB=BC=AC,则AE与EF之间的数量关系是什么;
(2)如图2,若AB=BC,你在(1)中得到的结论是否发生变化?写出猜想,并加以证明;
(3)如图3,若AB=kBC,你在(1)中得到的结论是否发生变化?写出猜想不用证明。
【答案】(1)AE=EF
(2)猜想:(1)中结论没有发生变化,即仍然为AE=EF(过点E作EH∥AB,可证
△AEH≌△FEC)
(3)猜想:(1)中的结论发生变化,为AE=kEF
8.(2010 浙江省温州市)(本题l2分)如图,抛物线y=ax2+bx经过点A(4,0),B(2,2)。连结OB,AB.
(1)求该抛物线的解析式;
(2)求证:△OAB是等腰直角三角形;
(3)将△OAB绕点0按顺时针方向旋转l35°得到△0A′B′,写出△0A′B′的中点
P的出标.试判断点P是否在此抛物线上,并说明理由.
【答案】
9.(2010 福建德化)(12分)在△ABC中,AB=BC=2,∠ABC=120°,将△ABC绕点B顺时针旋转角α(0<α<120°),得△A1BC1,交AC于点E,AC分别交A1C1、BC于D、F两点.
(1)如图①,观察并猜想,在旋转过程中,线段EA1与FC有怎样的数量关系?并证明你的结论;
(2)如图②,当=30°时,试判断四边形BC1DA的形状,并说明理由;
(3)在(2)的情况下,求ED的长.
C1
A1
F
E
D
C
B
A
图①
C1
A1
F
E
D
C
B
A
图②
【答案】(1);提示证明
(2)①菱形(证明略)
(3)过点E作EG⊥AB,则AG=BG=1
在中,
由(2)知AD=AB=2 ∴
10.(2010山东临沂)如图,二次函数的图象与轴交于,两点,且与轴交于点.
(1)求该抛物线的解析式,并判断的形状;
(2)在轴上方的抛物线上有一点,且以四点为顶点的四边形是等腰梯形,请直接写出点的坐标;
(3)在此抛物线上是否存在点,使得以四点为顶点的四边形是直角梯形?若存在,求出点的坐标;若不存在,说明理由.
第26题图
【答案】解:根据题意,将A(,0),B(2,0)代入y=-x2+ax+b中,
得
解这个方程,得
所以抛物线的解析式为y=-x2+x+1.
当x=0时,y=1.所以点C的坐标为(0,1)。
所以在△AOC中,AC==.
在△BOC中,BC==.
AB=OA+OB=.
因为AC2+BC2=.
所以△ABC是直角三角形。
图1
(2)点D的坐标是.
(3)存在。
由(1)知,AC⊥BC,
① 若以BC为底边,则BC∥AP,如图(1)所示,可求得直线BC的解析式为
.
直线AP可以看作是由直线AC平移得到的,所以设直线AP的解析式为,
将A(,0)代入直线AP的解析式求得b=,所以直线AP的解析式为.
因为点P既在抛物线上,又在直线AP上,所以点P的纵坐标相等,即-x2+x+1=.
解得(不合题意,舍去).
图2
当x=时,y=.
所以点P的坐标为(,).
②若以AC为底边,则BP∥AC,如图(2)所示,可求得直线AC的解析式为
.
直线BP可以看作是由直线AC平移得到的,所以设直线BP的解析式为,
将B(2,0)代入直线BP的解析式求得b=-4,所以直线BP的解析式为y=2x-4.
因为点P既在抛物线上,又在直线BP上,所以点P的纵坐标相等,即-x2+x+1=2x-4
解得(不合题意,舍去).
当x=-时,y=-9.
所以点P的坐标为(-,-9).
综上所述,满足题目的点P的坐标为(,)或(-,-9).
11.(2010湖南衡阳)如图,在正方形ABCD中,点E、F分别在BC、CD上移动,但A到EF的距离AH始终保持与AB长相等,问在E、F移动过程中:
(1)∠EAF的大小是否有变化?请说明理由.
(2)△ECF的周长是否有变化?请说明理由.
【答案】不变,理由是:在Rt△ABE和Rt△AHE中,AB=AH,AE=AE,所以Rt△ABE∽Rt△AHE,所以HE=BE,同理HF=DF.所以△ECF的周长=EF+CE+CF=BC+DC.可见△ECF的周长等于正方形边长的两倍.
12.(2010 黄冈)(15分)已知抛物线顶点为C(1,1)且过原点O.过抛物线上一点P(x,y)向直线作垂线,垂足为M,连FM(如图).
(1)求字母a,b,c的值;
(2)在直线x=1上有一点,求以PM为底边的等腰三角形PFM的P点的坐标,并证明此时△PFM为正三角形;
(3)对抛物线上任意一点P,是否总存在一点N(1,t),使PM=PN恒成立,若存在请求出t值,若不存在请说明理由.
【答案】(1)a=-1,b=2,c=0
(2)过P作直线x=1的垂线,可求P的纵坐标为,横坐标为.此时,MP=MF=PF=1,故△MPF为正三角形.
(3)不存在.因为当t<,x<1时,PM与PN不可能相等,同理,当t>,x>1时,PM与PN不可能相等.
13.(2010 山东莱芜)在 平行四边形 ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连结EG、GF、FH、HE.
(1)如图①,试判断四边形EGFH的形状,并说明理由;
(2)如图②,当EF⊥GH时,四边形EGFH的形状是 ;
(3)如图③,在(2)的条件下,若AC=BD,四边形EGFH的形状是 ;
(4)如图④,在(3)的条件下,若AC⊥BD,试判断四边形EGFH的形状,并说明理由.
H
G
F
E
O
D
C
B
A
图①
H
G
F
E
O
D
C
B
A
图②
A
B
C
D
O
E
F
G
H
图③
A
B
C
D
O
E
F
G
H
图④
(第23题图)
【答案】解:(1)四边形EGFH是平行四边形.
证明:∵ ABCD的对角线AC、BD交于点O.
∴点O是 ABCD的对称中心.
∴EO=FO,GO=HO.
∴四边形EGFH是平行四边形.
(2)菱形.
(3)菱形.
(4)四边形EGFH是正方形.
证明:∵AC=BD,∴ ABCD是矩形. 又∵AC⊥BD, ∴ ABCD是菱形.
∴ ABCD是正方形,∴∠BOC=90°,∠GBO=∠FCO=45°.OB=OC.
∵EF⊥GH ,∴∠GOF=90°.∴∠BOG=∠COF.
∴△BOG≌△COF.∴OG=OF,∴GH=EF.
由(1)知四边形EGFH是平行四边形,又∵EF⊥GH,EF=GH.
∴四边形EGFH是正方形.
14.(2010江西)如图,已知经过原点的抛物线y=-2x2+4x与x轴的另一交点为A,现将它向右平移m(m>0)个单位,所得抛物线与x轴交与C、D两点,与原抛物线交与点P.
(1)求点A的坐标,并判断△PCA存在时它的形状(不要求说理)
(2)在x轴上是否存在两条相等的线段,若存在,请一一找出,并写出它们的长度(可用含m的式子表示);若不存在,请说明理由;
(3)△CDP的面积为S,求S关于m的关系式。
x
y
D
A
C
O
P
【答案】解:(1)令-2x2+4x=0得x1=0,x2=2
∴点A的坐标是(2,0),
△PCA是等腰三角形,
(2)存在。
OC=AD=m,OA=CD=2,
(3)当0
2时,如图2
作PH⊥x轴于H,设,
∵A(2,0),C(m,0),
∴AC=m-2,∴AH=
∴=OH= = ,
把把=代入y=-2x2+4x,得
得, =
∵CD=OA=2,
∴.
15.(2010 武汉 )如图1,抛物线经过点A(-1,0),C(0,)两点,且与x轴的另一交点为点B.
(1)求抛物线解析式;
(2)若抛物线的顶点为点M,点P为线段AB上一动点(不与B重合),Q在线段MB上移动,且∠MPQ=45°,设OP=x,MQ=,求于x的函数关系式,并且直接写出自变量的取值范围;
(3)如图2,在同一平面直角坐标系中,若两条直线x=m,x=n分别与抛物线交于E、G两点,与(2)中的函数图像交于F、H两点,问四边形EFHG能否为平行四边形?若能,求出m、n之间的数量关系;若不能,请说明理由.
图 1
图 2
25.【答案】(1);
(2)由顶点M(1,2)知∠PBM=45°,易证△MBP∽△MPQ得,得,即;
(3)存在,设点E、G是抛物线分别与直线x=m,x=n的交点,则、,同理、,.由四边形EFHG为平行四边形得EG=FH,即,由,因此,四边形EFHG可以为平行四边形,m、n之间的数量关系是m+n=2(0≤m≤2,且m≠1).
16.(2010浙江湖州)如图,已知在矩形ABCD中,AB=2,BC=3,P是线段AD边上任意一点(不含端点A,D),连接PC,过点P作PE⊥PC交AB于E.(第25题)
(1)在线段AD上是否存在不同于P的点Q,使得QC⊥QE?若存在,
求线段AP与AQ之间的数量关系;若不存在,请说明理由;
(2)当点P在AD上运动时,对应的点E也随之在AB上运动,求BE的取值范围.
【答案】(1)存在,理由如下:假设存在这样的点Q,∵FE⊥PC,∴∠APE+∠DPC=90°,∵∠D=90°,
∴∠DPC+∠DCP=90°,∴△PAE∽△PDC,∴,∴,同理可得,∴,即,
∴,∴,
∴
∵AP≠AQ,∴AP+AQ=3.∵AP≠AQ,∴AP≠,即P不能是AD的中点,∴当P是AD的中点时,满足条件的Q点不存在,故,当P不是AD的中点时,总存在这样的点Q满足条件,此时AP+AQ=3.
(2)设AP=x,BE=y,则DP=3-x,AE=2-y,又PE⊥PC,∴△PAE∽△PDC,∴,即,∴,当时,y有最小值,y的最小值为,又E在AB上运动,且AB=2,∴BE的取值范围是≤BE<2.
17.(2010湖北荆门)已知一次函数y=的图象与x轴交于点A.与轴交于点;二次函数图象与一次函数y=的图象交于、两点,与轴交于、两点且点的坐标为
(1)求二次函数的解析式;
(2)求四边形BDEF的面积S;
(3)在轴上是否存在点P,使得△是以为直角顶点的直角三角形?若存在,求出所有的点,若不存在,请说明理由。
【答案】解:(1)∵ 由题意知:当x=0时,y=1, ∴B(0,1),当y=0时,x=-2, ∴A(-2,0)
∴解得,所以
(2)当y=0时, ,解得x1=1,x2=2, ∴D(1,0) E(2,0) ∴AO=3,AE=4. S=S△CAE-S△ABD,S=,S=4.5,
(3)存在点P(a,0),当P为直角顶点时,如图,过C作CF⊥x轴于F, ∵Rt△BOP∽Rt△PFC,
由题意得,AD=6,OD=1,易知,AD∥BE,
∴.即,整理得:a2-4a-3=0,解得a=1或a=3,所以所求P点坐标为(1,0)或(3,0).综上所述,满足条件的点P有两个.
18.(2010湖南常德)如图10,若四边形ABCD、四边形GFED都是正方形,显然图中有AG=CE,AG⊥CE.
(1)当正方形GFED绕D旋转到如图11的位置时,AG=CE是否成立?若成立,请给出证明;若不成立,请说明理由.
(2)当正方形GFED绕D旋转到如图12的位置时,延长CE交AG于H,交AD于M.
① 求证:AG⊥CH;
B
A
C
D
E
F
G
H
图12
A
B
C
D
E
F
G
图11
②当AD=4,DG=时,求CH的长.
A
B
C
D
E
F
G
图10
M
【答案】解:(1)成立.
四边形、四边形是正方形,
∴
∠∠.
∴∠90°-∠∠.
∴△△.
∴.
A
B
C
D
E
F
G
图11
B
A
C
D
E
F
G
1
2
图12
H
P
M
(2)①类似(1)可得△△,
∴∠1=∠2
又∵∠=∠.
∴∠∠=.
即
② 解法一: 过作于,
由题意有,
∴,则∠1=.
而∠1=∠2,∴∠2==∠1=.
∴ ,即.
在Rt中,==,
而∽,∴, 即,
∴.
再连接,显然有,
∴.
所求的长为.
B
A
C
D
E
F
G
1
2
图12
H
P
M
解法二:研究四边形ACDG的面积
过作于,
由题意有,
∴,.
而以CD为底边的三角形CDG的高=PD=1,
,
∴4×1+4×4=×CH+4 ×1.
∴=.
19.(2010湖南郴州)如图(1),抛物线与y轴交于点A,E(0,b)为y轴上一动点,过点E的直线与抛物线交于点B、C.
(1)求点A的坐标;
(2)当b=0时(如图(2)),与的面积大小关系如何?当时,上述关系还成立吗,为什么?
(3)是否存在这样的b,使得是以BC为斜边的直角三角形,若存在,求出b;若不存在,说明理由.
第26题
图(1)
图(2)
【答案】(1)将x=0,代入抛物线解析式,得点A的坐标为(0,-4)
(2)当b=0时,直线为,由解得,
所以B、C的坐标分别为(-2,-2),(2,2)
,
所以(利用同底等高说明面积相等亦可)
当时,仍有成立. 理由如下
由,解得,
所以B、C的坐标分别为(-,-+b),(,+b),
作轴,轴,垂足分别为F、G,则,
而和是同底的两个三角形,
所以.
(3)存在这样的b.
因为
所以
所以,即E为BC的中点
所以当OE=CE时,为直角三角形
因为
所以 ,而
所以,解得,
所以当b=4或-2时,ΔOBC为直角三角形.
20.(2010江苏常州)如图,已知二次函数的图像与轴相交于点A、C,与轴相较于点B,A(),且△AOB∽△BOC。
(1)求C点坐标、∠ABC的度数及二次函数的关系是;
(2)在线段AC上是否存在点M()。使得以线段BM为直径的圆与边BC交于P点(与点B不同),且以点P、C、O为顶点的三角形是等腰三角形?若存在,求出的值;若不存在,请说明理由。
【答案】
21.(2010四川 巴中)如图12已知△ABC中,∠ACB=90°以AB 所在直线为x 轴,过c 点的直线为y 轴建立平面直角坐标系.此时,A 点坐标为(一1 , 0), B 点坐标为(4,0 )
(1)试求点C 的坐标
(2)若抛物线过△ABC的三个顶点,求抛物线的解析式.
(3)点D( 1,m )在抛物线上,过点A 的直线y=-x-1 交(2)中的抛物线于点E,那么在x轴上点B 的左侧是否存在点P,使以P、B、D为顶点的三角形与△ABE 相似?若存在,求出P点坐标;若不存在,说明理由。
D
G
H
【答案】(1)∵∠ACB=90°,CO⊥AB,△ACO∽△CBO,∴,CO=2,
则C(0,2);
(2)抛物线过△ABC的三个顶点,则,∴,抛物线的解析式为;
(3)点D( 1,m )在抛物线上,,∴D(1,3),把直线y=-x-1与抛物线联立成方程组∴,
∴E(5,-6),过点D作DH垂直于x轴,过点E作EG垂直于x轴,DH=BH=3,∴∠DBH=45°,
BD=,AG=EG=6, ∴∠EAG=45°,AE=,
当P在B的右侧时,∠DBP=135°≠∠ABE,两个三角形不相似,所以P点不存在;
当P 在B的左侧时
ⅰ) △DPB∽△EBA时,,,∴P的坐标为(,0),
ⅱ) △DPB∽△BEA时, ,,∴P的坐标为(,0),
所以点P的坐标为(,0)或(,0)。
22.(2010四川宜宾)将直角边长为6的等腰Rt△AOC
放在如图所示的平面直角坐标系中,点O为坐标原点,点C、A分别在x、y轴的正半轴上,一条抛物线经过点A、C及点B(–3,0).
(1)求该抛物线的解析式;
(2)若点P是线段BC上一动点,过点P作AB的平行线交AC于点E,连接AP,当
△APE的面积最大时,求点P的坐标;
(3)在第一象限内的该抛物线上是否存在点G,使△AGC的面积与(2)中△APE的最
大面积相等?若存在,请求出点G的坐标;若不存在,请说明理由.
【答案】解:(1)由题意知:A(0,6),C(6,0),
设经过点A、B、C的抛物线解析式为y=ax2+bx+c
24题图
则:
解得:
∴该抛物线的解析式为
(2)如图:设点P(x,0),
∵PE∥AB,∴△CPE∽△ABC,
∴
又∵S△ABC=BC×OA=27
∴
∴S△CPE==
S△ABP=BP×OA=3x+9
设△APE的面积为S
则S= S△ABC—S△ABP—S△CPE=
当x=时,S最大值为
∴点P的坐标为(,0)
全品中考网
(3)假设存在点G(x,y),使△AGC的面积与(2)中△APE的最大面积相等.
在(2)中,△APE的最大面积为,过点G做GF垂直y轴与点F.
①当y>6时,S△AGC=S梯形GFOC—S△GFA—S△AOC=(x+6)y—x(y-6)—×6×6
=3x+3y-18
即3x+3y-18=,
又∵点G在抛物线上,,
∴3x+3-18=
解得:,当x=时,y=,当x=时,y=.
又∵y>6,∴
点G的坐标为(,)
②当y<6时,如图:
S△AGC=S△GAF+S梯形GFOC—S△AOC=x(6—y)+-18=3x+3y-18
即3x+3y-18=,
又∵点G在抛物线上,,
∴3x+3-18=
解得:,当x=时,y=,当x=时,y=.
又因为y<6,所以点G的坐标为(,).
综和①②所述,点G的坐标为(,)和(,).
(3)解法2:可以向x轴作垂线,构成了如此下图的图形:
则阴影部分的面积等于S△AGC=S△GCF+S梯形AGFO—S△AOC
下面的求解过程略.这样作可以避免了分类讨论.
23.(2010邵阳)阅读下列材料,然后解答问题。
经过正四边形(即正方形)各顶点的圆叫作这个正四边形的外接圆。圆心是正四边形的对称中心,这个正四边形叫作这个圆的内接正四边形。
如图(十三),已知正四边形ABCD的外接圆⊙O,⊙O的面积为S,正四边形ABCD的面积为S,以圆心O为顶点作∠MON,使∠MON=90°,将∠MON绕点O旋转,OM、ON分别与⊙O相交于点E、F,分别与正四边形ABCD的边相交于点G、H。设OE、OF、及正四边形ABCD的边围成的图形(图中阴影部分)的面积为S
(1)当OM经过点A时(如图①),则S、S、S之间的关系为:S= (用含S、S的代数式表示);
(2)当OM⊥AB时(如图②),点G为垂足,则(1)中的结论仍然成立吗?请说明理由。
(3)当∠MON旋转到任意位置时(如图③,)则(1)中的结论仍然成立吗?请说明理由.
图(十三)
【答案】解:(1)
(2)成立。理由:连OB,可证图中的两个阴影部分的面积之和等于图①的阴影部分的面积
(3)成立。过点O分别作AB、BC的垂线交AB、BC于点P、Q,交圆于点X、Y,可证直角三角形OPG全等于直角三角形OQH,可说明两阴影部分面积之和等于图①的阴影部分面积.
24.(2010湖北恩施自治州) 如图,在平面直角坐标系中,二次函数的图象与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
(1)求这个二次函数的表达式.
(2)连结PO、PC,并把△POC沿CO翻折,得到四边形POPC, 那么是否存在点P,使四边形POPC为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形 ABPC的面积最大并求出此时P点的坐标和四边形ABPC的最大面积.
【答案】解:(1)将B、C两点的坐标代入得
解得:
所以二次函数的表达式为:
(2)存在点P,使四边形POPC为菱形.设P点坐标为(x,),
PP交CO于E
若四边形POPC是菱形,则有PC=PO.
连结PP 则PE⊥CO于E,
∴OE=EC=
∴=.
∴=
解得=,=(不合题意,舍去)
∴P点的坐标为(,)…………………………8分
(3)过点P作轴的平行线与BC交于点Q,与OB交于点F,
设P(x,),
易得,直线BC的解析式为
则Q点的坐标为(x,x-3).
=
当时,四边形ABPC的面积最大
此时P点的坐标为,四边形ABPC的
面积.
25.(2010云南红河哈尼族彝族自治州)如图6,在正方形ABCD中,G是BC上的任意一点,(G与B、C两点不重合),E、F是AG上的两点(E、F与A、G两点不重合),若AF=BF+EF,∠1=∠2,请判断线段DE与BF有怎样的位置关系,并证明你的结论.
【答案】解:根据题目条件可判断DE//BF.
证明如下:
∵四边形ABCD是正方形,
∴AB=AD,∠BAF+∠2=90°.
∵AF=AE+EF,又AF=BF+EF
∴AE=BF
∵∠1=∠2,∴△ABF≌△DAE(SAS).
∴∠AFB=∠DEA,∠BAF=∠ADE.
∴∠ADE+∠2=90°,
∴∠AED=∠BFA=90°.
∴DE//BF.
26.(2010河南)如图,直线y=x+6与反比例函数y=等(x>0)的图象交于A(1,6),B(a,3)两点.
(1)求、的值;
(2)直接写出x +6一 >0时的取值范围;
(3)如图,等腰梯形OBCD中,BC∥OD,OB=CD,OD边在x轴上,过点C作CE⊥OD于E,CE和反比例函数的图象交于点P.当梯形OBCD的面积为l2时,请判断PC和PE的大小关系,并说明理由.
【答案】(1)由题意知 k2 = 1×6 = 6
∴反比例函数的解析式为 y = .
又B(a,3)在y = 的图象上,∴a = 2 ∴B(2,3).
∵ 直线y = k1x + b 过A(1,6),B(2,3)两点,
∴ ∴
(2)x 的取值范围为1< x < 2.
(3)当S梯形OBCD = 12时,PC= PE
设点P的坐标为(m,n),∵BC∥OD,CE⊥OD,BO = CD,B(2,3).
∴C(m,3),CE = 3,BC = m – 2,OD = m +2.
∴当S梯形OBCD = ,即12 =
∴m = 4 .又mn = 6 ,∴n = .即PE = CE.
∴PC = PE.
27.(2010四川乐山)在△ABC中,D为BC的中点,O为AD的中点,直线l过点O.过A、B、C三点分别做直线l的垂线,垂足分别是G、E、F,设AG=h1,BE=h2,CF=h3.
(1)如图(12.1),当直线l⊥AD时(此时点G与点O重合).求证:h2+h3= 2h1;
(2)将直线l绕点O旋转,使得l与AD不垂直.
①如图(12.2),当点B、C在直线l的同侧时,猜想(1)中的结论是否成立,请说明你的理由;
②如图(12.3),当点B、C在直线l的异侧时,猜想h1、h2、h3满足什么关系.(只需写出关系,不要求说明理由)
h2
h1
E
F
G
O
C
A
B
D
h3
l
h3
h1
h2
E
F
l
C
A
B
D
O
(G)
O
h2
h1
h3
F
E
G
l
C
A
B
D
图(12.3)
图(12.2)
图(12.1)
【答案】25.(1)证明:∵BE⊥l,GF⊥l,
∴四边形BCFE是梯形.
又∵GD⊥l,D是BC的中点,
∴DG是梯形的中位线,
∴BE+CF=2DG.
又O为AD的中点,∴AG=DG,
∴BE+CF=2AG.
即h2+h3= 2h1.
(2)成立.
证明:过点D作DH⊥l,垂足为H,
∴∠AGO=∠DHO=Rt∠,∠AOG=∠DOH,OA=OD,
∴△AGO≌△DHO,
∴DH=AG.
又∵D为BC的中点,由梯形的中位线性质,
得2 DH=BE+CF,即2 AG =BE+CF,
∴h2+h3= 2h1成立.
(3)h1、h2、h3满足关系:h2-h3= 2h1.
(说明:(3)问中,只要是正确的等价关系都得分)
28.(2010江苏徐州)如图,已知二次函数y=的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.
(1)点A的坐标为_______ ,点C的坐标为_______ ;
(2)线段AC上是否存在点E,使得△EDC为等腰三角形?若存在,求出所有符合条件的点E的坐标;若不存在,请说明理由;
(3)点P为x轴上方的抛物线上的一个动点,连接PA、PC,若所得△PAC的面积为S,则S取何值时,相应的点P有且只有2个?
【答案】
29.(2010云南昆明)在平面直角坐标系中,抛物线经过O(0,0)、A(4,0)、B(3,)三点.
(1)求此抛物线的解析式;
(2)以OA的中点M为圆心,OM长为半径作⊙M,在(1)中的抛物线上是否存在这样的点P,过点P作⊙M的切线l ,且l与x轴的夹角为30°,若存在,请求出此时点P的坐标;若不存在,请说明理由.(注意:本题中的结果可保留根号)
【答案】解:(1)设抛物线的解析式为:
由题意得:
解得:
∴抛物线的解析式为:
(2)存在
l′
抛物线的顶点坐标是,作抛物线和⊙M(如图),
设满足条件的切线 l 与 x 轴交于点B,与⊙M相切于点C
连接MC,过C作CD⊥ x 轴于D
∵ MC = OM = 2, ∠CBM = 30°, CM⊥BC
∴∠BCM = 90° ,∠BMC = 60° ,BM = 2CM = 4 , ∴B (-2, 0)
在Rt△CDM中,∠DCM = ∠CDM - ∠CMD = 30°
∴DM = 1, CD = = ∴ C (1, )
设切线 l 的解析式为:,点B、C在 l 上,可得:
解得:
∴切线BC的解析式为:
∵点P为抛物线与切线的交点
由 解得:
∴点P的坐标为:,
∵ 抛物线的对称轴是直线
此抛物线、⊙M都与直线成轴对称图形
于是作切线 l 关于直线的对称直线 l′(如图)
得到B、C关于直线的对称点B1、C1
l′满足题中要求,由对称性,得到P1、P2关于直线的对称点:
,即为所求的点.
∴这样的点P共有4个:,,,
30.(2010四川内江)如图,抛物线y=mx2―2mx―3m(m>0)与x轴交于A、B两点, 与y轴交于C点.
(1)请求抛物线顶点M的坐标(用含m的代数式表示),A,B两点的坐标;
(2)经探究可知,△BCM与△ABC的面积比不变,试求出这个比值;
(3)是否存在使△BCM为直角三角形的抛物线?若存在,请求出;如果不存在,请说明理由..
x
M
A
B
C
y
O
【答案】解:(1)∵y=mx2―2mx―3m=m(x2―2x―3)=m(x-1)2―4m,
∴抛物线顶点M的坐标为(1,―4m) 2分
∵抛物线y=mx2―2mx―3m(m>0)与x轴交于A、B两点,
∴当y=0时,mx2―2mx―3m=0,
∵m>0,
∴x2―2x―3=0,
解得x1=-1,x,2=3,
∴A,B两点的坐标为(-1,0)、(3,0). 4分
(2)当x=0时,y=―3m,
∴点C的坐标为(0,-3m),
∴S△ABC=×|3-(-1)|×|-3m|=6|m|=6m, 5分
过点M作MD⊥x轴于D,则OD=1,BD=OB-OD=2,MD=|-4m |=4m.
x
M
A
B
C
y
O
D
N
∴S△BCM=S△BDM +S梯形OCMD-S△OBC
=BD·DM+(OC+DM)·OD-OB·OC
=×2×4m+(3m+4m)×1-×3×3m=3m, 7分
∴ S△BCM:S△ABC=1∶2. 8分
(3)存在使△BCM为直角三角形的抛物线.
过点C作CN⊥DM于点N,则△CMN为Rt△,CN=OD=1,DN=OC=3m,
∴MN=DM-DN=m,
∴CM2=CN2+MN2=1+m2,
在Rt△OBC中,BC2=OB2+OC2=9+9m2,
在Rt△BDM中,BM2=BD2+DM2=4+16m2.
①如果△BCM是Rt△,且∠BMC=90°时,CM2+BM2=BC2,
即1+m2+4+16m2=9+9m2,
解得 m=±,
∵m>0,∴m=.
∴存在抛物线y=x2-x-使得△BCM是Rt△; 10分
②①如果△BCM是Rt△,且∠BCM=90°时,BC2+CM2=BM2.
即9+9m2+1+m2=4+16m2,
解得 m=±1,
∵m>0,∴m=1.
∴存在抛物线y=x2-2x-3使得△BCM是Rt△;
③如果△BCM是Rt△,且∠CBM=90°时,BC2+BM2=CM2.
即9+9m2+4+16m2=1+m2,
整理得 m2=-,此方程无解,
∴以∠CBM为直角的直角三角形不存在.
(或∵9+9m2>1+m2,4+16m2>1+m2,∴以∠CBM为直角的直角三角形不存在.)
综上的所述,存在抛物线y=x2-x-和y=x2-2x-3使得△BCM是Rt△.
31.(2010 福建三明)已知抛物线经过点B(2,0)和点C(0,8),且它的对称轴是直线。
(1)求抛物线与轴的另一交点A坐标;(2分)
(2)求此抛物线的解析式;(3分)
(3)连结AC、BC,若点E是线段AB上的一个动点(与点A、点B)不重合,过点E作EF∥AC交BC于点F,连结CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式;
(4)在(3)的基础上试说明S是否存在最大值,若
存在,请求出S的最大值,并求出此时点E的
坐标,判断此时△BCE的形状;若不存在,请
说明理由。
【答案】(1)∵抛物线的对称轴是直线
∴由对称性可得A点的坐标为(-6,0) …………2分
(2)∵点C(0,8)在抛物线的图象上
将A(-6,0)、B(2,0)代入表达式得
解得 ∴所求解析式为
[也可用] …………5分
(3)依题意,AE=m,则BE=8-m
∵OA=6,OC=8,∴AC=10
∵EF//AC ∴≌
过点F作FG⊥AB,垂足为G,则
…………10分
(4)存在.理由如下:
∴当m=4时,S有最大值,S最大值=8 …………12分
∵m=4
∴点E的坐标为(——-2,0)
为等腰三角形 …………14分
32.(2010 湖北孝感) 如图,已知二次函数图像的顶点坐标为(2,0),直线与二次函数的图像交于A、B两点,其中点A在y轴上。
(1)二次函数的解析式为y= ;(3分)
(2)证明点不在(1)中所求的二次函数的图像上;(3分)
(3)若C为线段AB的中点,过C点作轴于E点,CE与二次函数的图像交于D点。
①y轴上存在点K,使以K、A、D、C为顶点的四边形是平行四边形,则K点的坐标是 ;(2分)
②二次函数的图像上是否存在点P,使得
?若存在,求出P点坐标;若不存在,请说明理由。(4分)
【答案】(1)解: …………3分
(2)证明:设点的图像上,
则有: …………4分
整理得
∴原方程无解 …………5分
的图象上 …………6分
说明:由
从而判断点不在二次函数图像上的同样给分。
(3)解:①; …………8分
②二次函数的图象上存在点P,使得
如图,过点B作轴于F,则BF//CE//AO,又C为AB中点,
…………9分
设,由题意有:
…………10分
解得 …………11分
33.(2010 云南玉溪)平面内的两条直线有相交和平行两种位置关系.
(1)如图a,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD,又因∠BOD是
△POD的外角,故∠BOD=∠BPD +∠D,得∠BPD=∠B-∠D.将点P移到AB、CD内部,如图b,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论;
图a
O
图b
(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系?(不需证明);
(3)根据(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数.
图c
图d
【答案】解:(1)不成立,结论是∠BPD=∠B+∠D.
延长BP交CD于点E,
∵AB∥CD. ∴∠B=∠BED.
又∠BPD=∠BED+∠D,
∴∠BPD=∠B+∠D. …………4分
(2)结论: ∠BPD=∠BQD+∠B+∠D. …………7分
(3)由(2)的结论得:∠AGB=∠A+∠B+∠E.
又∵∠AGB=∠CGF.
∠CGF+∠C+∠D+∠F=360°
∴∠A+∠B+∠C+∠D∠E+∠F=360°. …………11分
34.(2010 云南玉溪)如图10,在平面直角坐标系中,点A的坐标为(1,) ,△
AOB的面积是.
(1)求点B的坐标;
(2)求过点A、O、B的抛物线的解析式;
(3)在(2)中抛物线的对称轴上是否存在点C,使△AOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由;
(4)在(2)中轴下方的抛物线上是否存在一点P,过点P作轴的垂线,交直线AB于点D,线段OD把△AOB分成两个三角形.使其中一个三角形面积与四边形BPOD面积比为2:3 ?若存在,求出点P的坐标;若不存在,请说明理由.
y
A
0
B
图10
【答案】解:(1)由题意得:
∴B(-2,0) …………3分
(2)设抛物线的解析式为y=ax(x+2),代入点A(1, ),得,
∴ …………6分
C
A
B
O
y
x
(3)存在点C.过点A作AF垂直于x轴于点F,抛物线
的对称轴x= - 1交x轴于点E.当点C位于对称轴
与线段AB的交点时,△AOC的周长最小.
∵ △BCE∽△BAF,
…………9分
(4)存在. 如图,设p(x,y),直线AB为y=kx+b,则
,
∴直线AB为,
= |OB||YP|+|OB||YD|=|YP|+|YD|
=.
∵S△AOD= S△AOB-S△BOD =-×2×∣x+∣=-x+.
∴==.
∴x1=- , x2=1(舍去).
∴p(-,-) .
y
x
A
O
D
B
P
又∵S△BOD =x+,
∴ == .
∴x1=- , x2=-2.
P(-2,0),不符合题意.
∴ 存在,点P坐标是(-,-). …………12分
35.(2010 重庆江津)如图,抛物线与轴交于两点A(-1,0),B(1,0),与轴交于点C.
(1)求抛物线的解析式;
(2)过点B作BD∥CA与抛物线交于点D,求四边形ACBD的面积;
(3)在轴下方的抛物线上是否存在一点M,过M作MN⊥轴于点N,使以A、M、N为顶点的三角形与△BCD相似?若存在,则求出点M的坐标;若不存在,请说明理由.
【答案】解:(1)把A B代入得:
解得:
………………………………………………………………………3分
(2)令,得 ∴ ……………………………………………4分
∵OA=OB=OC= ∴BAC=ACO=BCO=ABC =
∵BD∥CA, ∴ABD=BAC
过点D作DE轴于E,则BDE为等腰直角三角形
令 ,则 ∴
∵点D在抛物线上 ∴
解得,(不合题意,舍去)
∴DE=
(说明:先求出直线BD的解析式,再用两个解析式联立求解得到点D的坐标也可)
∴四边形ACBD的面积=AB•OC +AB•DE
………………………………7分
(说明:也可直接求直角梯形ACBD的面积为4)
(3)存在这样的点M……………………………………………………………………8分
∵ABC=ABD= ∴DBC=
∵MN轴于点N, ∴ANM=DBC =
在Rt△BOC中,OB=OC= 有BC=
在Rt△DBE中,BE=DE= 有BD=
设M点的横坐标为,则M
①点M在轴左侧时,则
(ⅰ) 当AMN CDB时,有
∵
即 解得:(舍去)
则
(ⅱ) 当AMN DCB时,有
即 解得(舍去) (舍去)…………10分
② 点M在轴右侧时,则
(ⅰ) 当AMN DCB时,有
∵
∴
解得(舍去)
∴
(ⅱ) 当AMN CDB时,有
即 解得:(舍去)
∴
∴M点的坐标为…………………………12分
36.(2010青海西宁)八(1)班同学上数学活动课,利用角尺平分一个角(如图).设计了如下方案:
(Ⅰ)∠AOB是一个任意角,将角尺的直角顶点P介于射线OA、OB之间,移动角尺使角尺两边相同的刻度与M、N重合,即PM=PN,过角尺顶点P的射线OP就是∠AOB的平分线.
(Ⅱ)∠AOB是一个任意角,在边OA、OB上分别取OM=ON,将角尺的直角顶点P介于射线OA、OB之间,移动角尺使角尺两边相同的刻度与M、N重合,即PM=PN,过角尺顶点P的射线OP就是∠AOB的平分线.
(1)方案(Ⅰ)、方案(Ⅱ)是否可行?若可行,请证明;若不可行,请说明理由.
(2)在方案(Ⅰ)PM=PN的情况下,继续移动角尺,同时使PM⊥OA,PN⊥OB.此方案是否可行?请说明理由.
【答案】解:(1)方案(Ⅰ)不可行.缺少证明三角形全等的条件. ……………………………2分
(2)方案(Ⅱ)可行. ……………………………3分
证明:在△OPM和△OPN中
∴△OPM≌△OPN(SSS)
∴∠AOP=∠BOP(全等三角形对应角相等) ……………………………5分
(3)当∠AOB是直角时,此方案可行. ……………………………6分
∵四边形内角和为360°,又若PM⊥OA,PN⊥OB, ∠OMP=∠ONP=90°, ∠MPN=90°,
∴∠AOB=90°
∵若PM⊥OA,PN⊥OB,
且PM=PN
∴OP为∠AOB的平分线.(到角两边距离相等的点在这个角的角平分线上)
当∠AOB不为直角时,此方案不可行. …………8分
37.(2010鄂尔多斯)如图,四边形OABC是一张放在平面直角坐标系的矩形纸片,O为原点,点A在轴上,点C在y轴上,OA=15,OC=9,在AB上取一点M,使得△CBM沿CM翻折后,点B落在x轴上,记用N点。
(1) 求N点、M点的坐标;
(2)将抛物线y=x2-36向右平移a个(0
查看更多