上海华育中学中考数学模拟试题

上海华育中学中考数学模拟试题

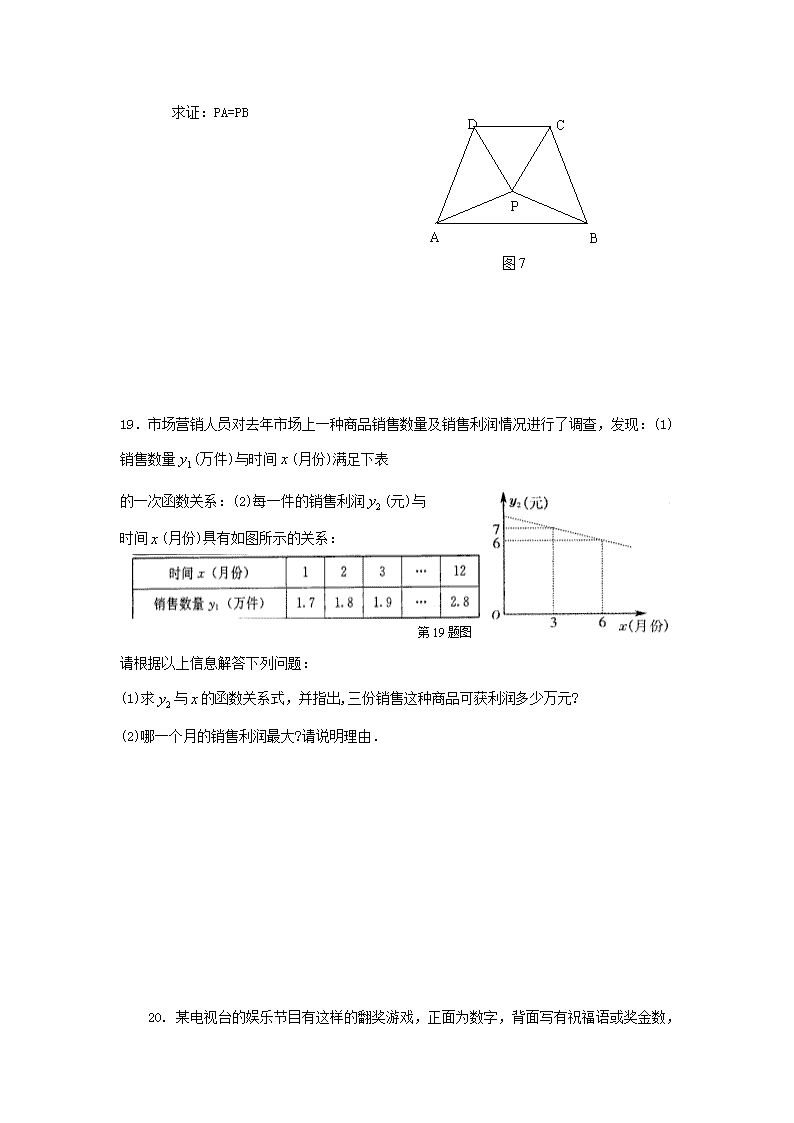
上海华育中学中考数学模拟试题 ‎ ‎ 一、选择题（本题满分30分，共10小题，每小题3分）‎ ‎1．的算术平方根是（ ）‎ Ａ．2 Ｂ． Ｃ．4 Ｄ．‎ ‎2.下列计算正确的是（ ）‎ ‎ A. B. ‎ C. D.‎ ‎3．一次数学测试后，随机抽取九年级二班5名学生的成绩如下：78，85，91，98，98．关于这组数据的错误说法是（　　）‎ Ａ．极差是20 Ｂ．众数是98 Ｃ．中位数是91 Ｄ．平均数是91‎ ‎4、下列各图中，不是中心对称图形的是（ ）‎ ‎5．要使二次根式有意义，应满足的条件是（　　）‎ Ａ． Ｂ． Ｃ． Ｄ．‎ ‎6．分式的值为１时，的值是（　　）‎ Ａ． Ｂ． Ｃ． Ｄ．‎ ‎7．不等式组的解集是　　　　　．‎ A、x＞2 B、x＞-3 C、x＜-3 D、无解 ‎8、下列四个命题中，假命题的是（ ）‎ A、对角线互相平分的四边形是平行四边形；B、三点确定一个圆；‎ C、圆既是轴对称图形，又是中心对称图形；D、三角形的内角和等于180度。‎ ‎9. 下列调查中，比较适合用普查而不适合抽样调查方式的是（ ）‎ A、调查一批显像管的使用寿命；B、调查“永春芦柑”的甜度和含水量；‎ C、调查我县居民的环保意识； D、调查你所在学校数学教师的年龄状况。‎ ‎10．圆的直径为12cm，圆心到直线的距离为7cm，则直线与圆的位置关系是（　　）‎ Ａ．相交 Ｂ．相切 Ｃ．相离 Ｄ．不能确定 二．填空：（共15分，每题3分）‎ ‎11．五角星绕中心点旋转一定的角度后能与自身完全重合，则其旋转的角度至少为_____________‎ ‎12、一个袋中装有两个红球三个白球，第一次摸出一个球放回，再任意摸出一个，则两次都摸到白球的概率为__ __；‎ ‎13．一次函数的图象过点（0 , -l ) ，且函数值随着自变量的增大而减小，写出一个符合这个条件的一次函数解析式: 。‎ ‎14.小亮从A点出发，沿直线前进10米后向左转30°，再沿直线前进10米，又向左转30°，……照这样走下去，他第一次回到出发地A点时，一共走了__________米。‎ ‎15、如图，半圆A和半圆B均与y轴相切于点O，其直径CD、EF均和x轴垂直，以O为顶点的两条抛物线分别经过点C、E和点D、F，则图中阴影部分的面积是 。‎ 三、解答题（本题满分55分，共8小题，其中16-21题各6分，，22题9分，22题10分）‎ ‎16.计算：‎ ‎17．解分式方程：‎ ‎18．在等腰梯形ABCD中，AB∥CD，P是梯形内一点，且PC=PD.‎ 图7‎ A B C D P 求证：PA=PB ‎19．市场营销人员对去年市场上一种商品销售数量及销售利润情况进行了调查，发现：(1)销售数量(万件)与时间(月份)满足下表 第19题图 的一次函数关系：(2)每一件的销售利润(元)与 时间(月份)具有如图所示的关系：‎ 请根据以上信息解答下列问题：‎ ‎(1)求与的函数关系式，并指出,三份销售这种商品可获利润多少万元?‎ ‎(2)哪一个月的销售利润最大?请说明理由．‎ ‎20.‎ ‎ 某电视台的娱乐节目有这样的翻奖游戏，正面为数字，背面写有祝福语或奖金数，如下面的表格．游戏的规则是：参加游戏的人可随意翻动一个数字牌，看背面对应的内容，就可以知道是得奖还是得到祝福语．‎ 祝你开心 万事如意 奖金1000元 身体健康 心想事成 奖金500元 奖金100元 生活愉快 谢谢参与 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎（1）写出“翻到奖金1000元”的概率；‎ ‎（2）写出“翻到奖金”的概率；‎ ‎（3）写出“翻不到奖金”的概率．‎ ‎21、为申办2010年冬奥会，须改变哈尔滨市的交通状况。在大直街拓宽工程中，要伐掉一棵树AB，在地面上事先划定以B为圆心，半径与AB等长的圆形危险区，现在某工人站在离B点3米远的D处，从C点测得树的顶端A点的仰角为60°，树的底部B点的俯角为30°. ‎ ‎ 问：距离B点8米远的保护物是否在危险区内？‎ ‎22.如图，已知二次函数的图像与x轴交于点A、点B(点B在X轴的正半轴上)，与y轴交于点C，其 ‎(第22题图)‎ 顶点为D，直线DC的函数关系式为，又tan∠OBC=1。‎ ‎(1) 求a、k的值；‎ ‎(2) 探究：在该二次函数的图像上是否存在点P(点P与点B、C补重合)，‎ 使得ΔPBC是以BC为一条直角边的直角三角形?若存在，求出点P 的坐标，若不存在，请你说明理由。‎ AB ‎⌒‎ ‎23.如图，在⊙M中， 所对的圆心角为1200，已知圆的半径为2cm，并建立如图所示的直角坐标系。‎ ‎（1）求圆心M的坐标；‎ ‎（2）求经过A，B，C三点的抛物线的解析式；‎ ‎（3）点D是弦AB所对的优弧上一动点，求四边形ACBD的最大面积；‎ y x A M O B C ‎（4）在（2）中的抛物线上是否存在一点P，使ΔPAB和ΔABC相似？若存在，求出点P的坐标；若不存在，请说明理由。‎