- 2021-05-10 发布 |
- 37.5 KB |
- 3页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2011中考数学第一轮切线的判定与性质考点专题测试题及答案6
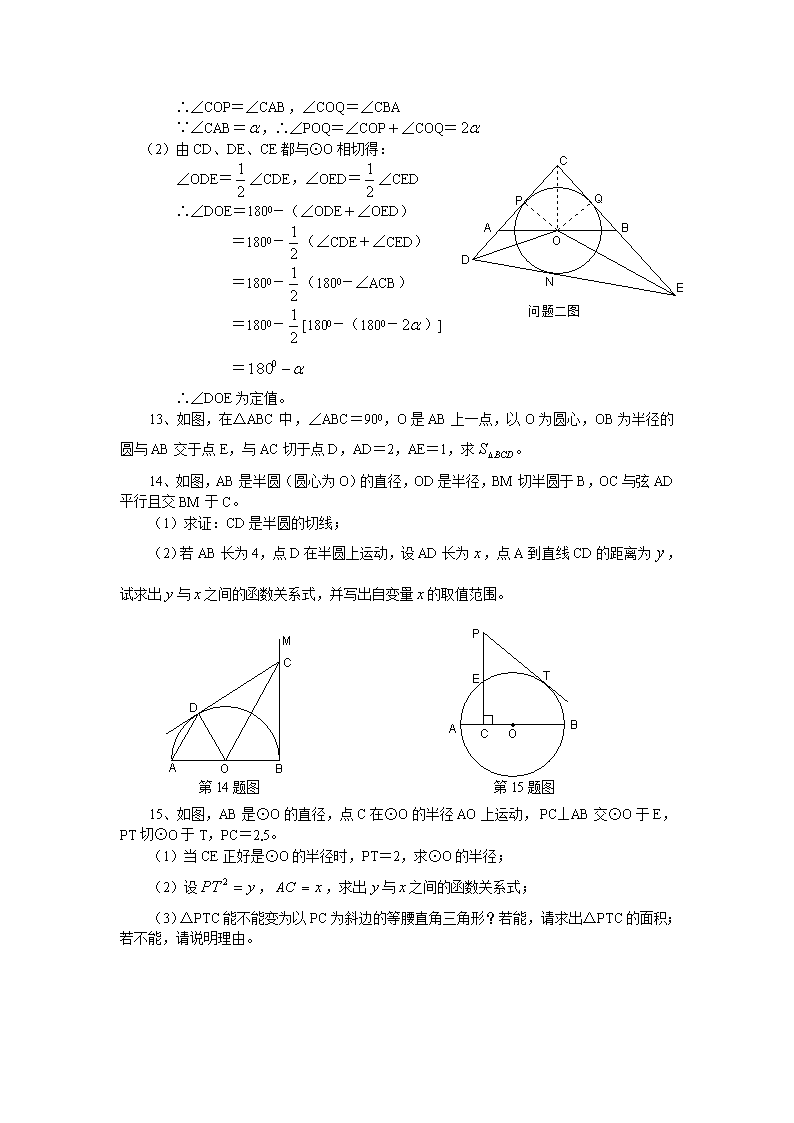
切线的判定与性质 知识考点: 1、掌握切线的判定及其性质的综合运用,在涉及切线问题时,常连结过切点的半径,切线的判定常用以下两种方法:一是连半径证垂直,二是作垂线证半径。 2、掌握切线长定理的灵活运用,掌握三角形和多边形的内切圆,三角形的内心。 精典例题: 【例1】如图,AC为⊙O的直径,B是⊙O外一点,AB交⊙O于E点,过E点作⊙O的切线,交BC于D点,DE=DC,作EF⊥AC于F点,交AD于M点。 (1)求证:BC是⊙O的切线; (2)EM=FM。 分析:(1)由于AC为直径,可考虑连结EC,构造直角三角形来解题,要证BC是⊙O的切线,证到∠1+∠3=900即可;(2)可证到EF∥BC,考虑用比例线段证线段相等。 证明:(1)连结EC,∵DE=CD,∴∠1=∠2 ∵DE切⊙O于E,∴∠2=∠BAC ∵AC为直径,∴∠BAC+∠3=900 ∴∠1+∠3=900,故BC是⊙O的切线。 (2)∵∠1+∠3=900,∴BC⊥AC 又∵EF⊥AC,∴EF∥BC ∴ ∵BD=CD,∴EM=FM 【例2】如图,△ABC中,AB=AC,O是BC的中点,以O为圆心的圆与AB相切于点D。求证:AC是⊙O的切线。 分析:由于⊙O与AC有无公共点未知,因此我们从圆心O向AC作垂线段OE,证OE就是⊙O的半径即可。 证明:连结OD、OA,作OE⊥AC于E ∵AB=AC,OB=OC,∴AO是∠BAC的平分线 ∵AB是⊙O的切线,∴OD⊥AB 又∵OE⊥AC,∴OE=OD ∴AC是⊙O的切线。 【例3】如图,已知AB是⊙O的直径,BC为⊙O的切线,切点为B,OC平行于弦AD,OA=。 (1)求证:CD是⊙O的切线; (2)求的值; (3)若AD+OC=,求CD的长。 分析:(1)要证CD是⊙O的切线,由于D在⊙O上,所以只须连结OD,证OD⊥DC即可;(2)求的值,一般是利用相似把转化为其它线段长的乘积,若其它两条线段长的乘积能求出来,则可完成;(3)由,AD+OC=可求出AD、OC,根据勾股定理即可求出CD。 证明:(1)连结OD,证∠ODC=900即可; (2)连结BD ∵AB为⊙O的直径,∴∠ADB=900 ∵∠OBC=900,∴∠ADB=∠OBC 又∠A=∠3,∴△ADB∽△OBC ∴ ∴ (3)由(2)知,又知AD+OC= ∴AD、OC是关于的方程的两根 解此方程得, ∵OC>,∴OC= ∴CD= 探索与创新: 【问题一】如图,以正方形ABCD的边AB为直径,在正方形内部作半圆,圆心为O,CG切半圆于E,交AD于F,交BA的延长线于G,GA=8。 (1)求∠G的余弦值; (2)求AE的长。 略解:(1)设正方形ABCD的边长为,FA=FE=6,在Rt△FCD中,,,解得。 ∴ ∵AB∥CD,∴∠G=∠FCD,∴ (2)连结BE,∵CG切半圆于E,∴∠AEG=∠GBE ∵∠G为公共角,∴△AEG∽△EBG ∴ 在Rt△AEB中,可求得 【问题二】如图,已知△ABC中,AC=BC,∠CAB=(定值),⊙O的圆心O在AB上,并分别与AC、BC相切于点P、Q。 (1)求∠POQ; (2)设D是CA延长线上的一个动点,DE与⊙O相切于点M,点E在CB的延长线上,试判断∠DOE的大小是否保持不变,并说明理由。 分析:(1)连结OC,利用直角三角形的性质易求∠POQ;(2)试将∠DOE用含的式子表示出来,由于为定值,则∠DOE为定值。 解:(1)连结OC ∵BC切⊙O于P、Q,∴∠1=∠2,OP⊥CA,OQ⊥CB ∵CA=CB,∴CO⊥AB ∴∠COP=∠CAB,∠COQ=∠CBA ∵∠CAB=,∴∠POQ=∠COP+∠COQ= (2)由CD、DE、CE都与⊙O相切得: ∠ODE=∠CDE,∠OED=∠CED ∴∠DOE=1800-(∠ODE+∠OED) =1800-(∠CDE+∠CED) =1800-(1800-∠ACB) =1800-[1800-(1800-)] = ∴∠DOE为定值。 13、如图,在△ABC中,∠ABC=900,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,AD=2,AE=1,求。 14、如图,AB是半圆(圆心为O)的直径,OD是半径,BM切半圆于B,OC与弦AD平行且交BM于C。 (1)求证:CD是半圆的切线; (2)若AB长为4,点D在半圆上运动,设AD长为,点A到直线CD的距离为,试求出与之间的函数关系式,并写出自变量的取值范围。 15、如图,AB是⊙O的直径,点C在⊙O的半径AO上运动, PC⊥AB交⊙O于E,PT切⊙O于T,PC=2.5。 (1)当CE正好是⊙O的半径时,PT=2,求⊙O的半径; (2)设,,求出与之间的函数关系式; (3)△PTC能不能变为以PC为斜边的等腰直角三角形?若能,请求出△PTC的面积;若不能,请说明理由。查看更多