中考数学压轴题抛物线及动点精选

中考数学压轴题抛物线及动点精选

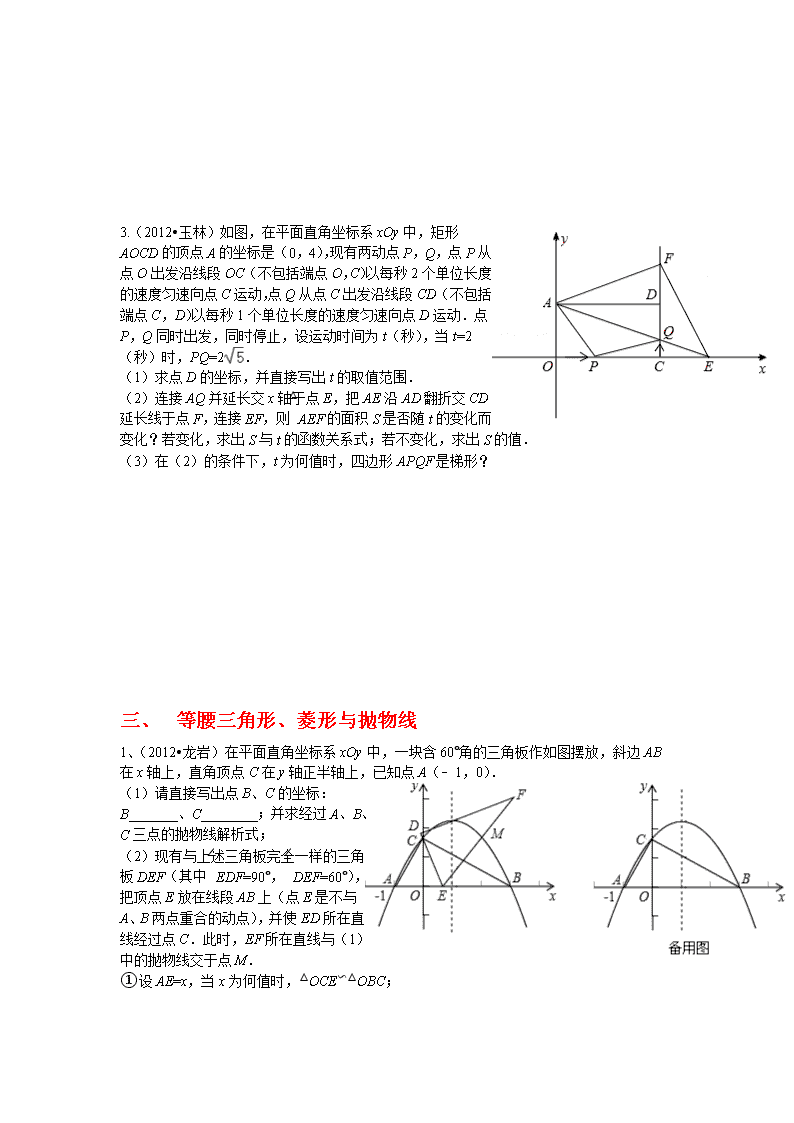
动点与抛物线专题复习 一、平行四边形与抛物线 ‎1、（2012•钦州）如图甲，在平面直角坐标系中，A、B的坐标分别为（4，0）、（0，3），抛物线y=x2+bx+c经过点B，且对称轴是直线x=﹣．‎ ‎（1）求抛物线对应的函数解析式；‎ ‎（2）将图甲中△ABO沿x轴向左平移到△DCE（如图乙），当四边形ABCD是菱形时，请说明点C和点D都在该抛物线上；‎ ‎（3）在（2）中，若点M是抛物线上的一个动点（点M不与点C、D重合），经过点M作MN∥y轴交直线CD于N，设点M的横坐标为t，MN的长度为l，求l与t之间的函数解析式，并求当t为何值时，以M、N、C、E为顶点的四边形是平行四边形．（参考公式：抛物线y=ax2+bx+c（a≠0）的顶点坐标为（﹣，），对称轴是直线x=﹣．）‎ ‎2、（2012•鸡西）如图，在平面直角坐标系中，已知Rt△AOB的两条直角边OA、OB分别在y轴和x轴上，并且OA、OB的长分别是方程x2﹣7x+12=0的两根（OA＜OB），动点P从点A开始在线段AO上以每秒1个单位长度的速度向点0运动；同时，动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动，设点P、Q运动的时间为t秒．‎ ‎（1）求A、B两点的坐标．‎ ‎（2）求当t为何值时，△APQ与△AOB相似，并直接写出此时点Q的坐标．‎ ‎（3）当t=2时，在坐标平面内，是否存在点M，使以A、P、Q、M为顶点的四边形是平行四边形？若存在，请直接写出M点的坐标；若不存在，请说明理由．‎ ‎3.（2012•恩施州）如图，已知抛物线y=﹣x2+bx+c与一直线相交于A（﹣1，0），C（2，3）两点，与y轴交于点N．其顶点为D．‎ ‎（1）抛物线及直线AC的函数关系式；‎ ‎（2）设点M（3，m），求使MN+MD的值最小时m的值；‎ ‎（3）若抛物线的对称轴与直线AC相交于点B，E为直线AC上的任意一点，过点E作EF∥BD交抛物线于点F，以B，D，E，F为顶点的四边形能否为平行四边形？若能，求点E的坐标；若不能，请说明理由；‎ ‎（4）若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值．‎ 二、 梯形与抛物线 ‎1、已知，在Rt△OAB中，∠OAB=90°，∠BOA=30°，AB=2．若以O为坐标原点，OA所在直线为x轴，建立如图所示的平面直角坐标系，点B在第一象限内．将Rt△OAB沿OB折叠后，点A落在第一象限内的点C处．‎ ‎（1）求点C的坐标；‎ ‎（2）若抛物线y=ax2+bx（a≠0）经过C、A两点，求此抛物线的解析式；‎ ‎（3）若上述抛物线的对称轴与OB交于点D，点P为线段DB上一动点，过P作y轴的平行线，交抛物线于点M，问：是否存在这样的点P，使得四边形CDPM为等腰梯形？若存在，请求出此时点P的坐标；若不存在，请说明理由．‎ ‎2、（2012•泉州）如图，O为坐标原点，直线l绕着点A（0，2）旋转，与经过点C（0，1）的二次函数y=x2+h的图象交于不同的两点P、Q．‎ ‎（1）求h的值；‎ ‎（2）通过操作、观察，算出△POQ的面积的最小值（不必说理）；‎ ‎（3）过点P、C作直线，与x轴交于点B，试问：在直线l的旋转过程中，四边形AOBQ是否为梯形？若是，请说明理由；若不是，请指出四边形的形状．‎ ‎3.（2012•玉林）如图，在平面直角坐标系xOy中，矩形AOCD的顶点A的坐标是（0，4），现有两动点P，Q，点P从点O出发沿线段OC（不包括端点O，C）以每秒2个单位长度的速度匀速向点C运动，点Q从点C出发沿线段CD（不包括端点C，D）以每秒1个单位长度的速度匀速向点D运动．点P，Q同时出发，同时停止，设运动时间为t（秒），当t=2（秒）时，PQ=2．‎ ‎（1）求点D的坐标，并直接写出t的取值范围．‎ ‎（2）连接AQ并延长交x轴于点E，把AE沿AD翻折交CD延长线于点F，连接EF，则△AEF的面积S是否随t的变化而变化？若变化，求出S与t的函数关系式；若不变化，求出S的值．‎ ‎（3）在（2）的条件下，t为何值时，四边形APQF是梯形？‎ 二、 等腰三角形、菱形与抛物线 ‎1、（2012•龙岩）在平面直角坐标系xOy中，一块含60°角的三角板作如图摆放，斜边AB在x轴上，直角顶点C在y轴正半轴上，已知点A（﹣1，0）．‎ ‎（1）请直接写出点B、C的坐标：B　 　、C　 　；并求经过A、B、C三点的抛物线解析式；‎ ‎（2）现有与上述三角板完全一样的三角板DEF（其中∠EDF=90°，∠DEF=60°），把顶点E放在线段AB上（点E是不与A、B两点重合的动点），并使ED所在直线经过点C．此时，EF所在直线与（1）中的抛物线交于点M．‎ ‎①设AE=x，当x为何值时，△OCE∽△OBC；‎ ‎②在①的条件下探究：抛物线的对称轴上是否存在点P使△PEM是等腰三角形？若存在，请写出点P的坐标；若不存在，请说明理由．‎ ‎3、（2012•湛江）如图，在平面直角坐标系中，直角三角形AOB的顶点A、B分别落在坐标轴上．O为原点，点A的坐标为（6，0），点B的坐标为（0，8）．动点M从点O出发．沿OA向终点A以每秒1个单位的速度运动，同时动点N从点A出发，沿AB向终点B以每秒个单位的速度运动．当一个动点到达终点时，另一个动点也随之停止运动，设动点M、N运动的时间为t秒（t＞0）．‎ ‎（1）当t=3秒时．直接写出点N的坐标，并求出经过O、A、N三点的抛物线的解析式；‎ ‎（2）在此运动的过程中，△MNA的面积是否存在最大值？若存在，请求出最大值；若不存在，请说明理由；‎ ‎（3）当t为何值时，△MNA是一个等腰三角形？‎ ‎4、如图，直线l1经过点A（﹣1，0），直线l2经过点B（3，0），l1、l2均为与y轴交于点C（0，），抛物线y=ax2+bx+c（a≠0）经过A、B、C三点．‎ ‎（1）求抛物线的函数表达式；‎ ‎（2）抛物线的对称轴依次与x轴交于点D、与l2交于点E、与抛物线交于点F、与l1交于点G．求证：DE=EF=FG；‎ ‎（3）若l1⊥l2于y轴上的C点处，点P为抛物线上一动点，要使△PCG为等腰三角形，请写出符合条件的点P的坐标，并简述理由．‎ ‎5、如图，在平面直角坐标系中，直角梯形OABC的边OC、OA分别与x轴、y轴重合，AB∥OC，∠AOC=90°，∠BCO=45°，BC=12，点C的坐标为（﹣18，0）．‎ ‎（1）求点B的坐标；‎ ‎（2）若直线DE交梯形对角线BO于点D，交y轴于点E，且OE=4，OD=2BD，求直线DE的解析式；‎ ‎（3）若点P是（2）中直线DE上的一个动点，在坐标平面内是否存在点Q，使以O、E、P、Q为顶点的四边形是菱形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．‎ ‎6、（2012•铁岭）如图，已知抛物线经过原点O和x轴上一点A（4，0），抛物线顶点为E，它的对称轴与x轴交于点D．直线y=﹣2x﹣1经过抛物线上一点B（﹣2，m）且与y轴交于点C，与抛物线的对称轴交于点F．‎ ‎（1）求m的值及该抛物线对应的解析式；‎ ‎（2）P（x，y）是抛物线上的一点，若S△ADP=S△ADC，求出所有符合条件的点P的坐标；‎ ‎（3）点Q是平面内任意一点，点M从点F出发，沿对称轴向上以每秒1个单位长度的速度匀速运动，设点M的运动时间为t秒，是否能使以Q、A、E、M四点为顶点的四边形是菱形？若能，请直接写出点M的运动时间t的值；若不能，请说明理由．‎ 二、 直角三角形与抛物线 ‎1、（2012•广州）如图，抛物线y=与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C．‎ ‎（1）求点A、B的坐标；‎ ‎（2）设D为已知抛物线的对称轴上的任意一点，当△ACD的面积等于△ACB的面积时，求点D的坐标；‎ ‎（3）若直线l过点E（4，0），M为直线l上的动点，当以A、B、M为顶点所作的直角三角形有且只有三个时，求直线l的解析式．‎ ‎2、（2012•河池）如图，在等腰三角形ABC中，AB=AC，以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系，抛物线y=﹣x2+x+4经过A、B两点．‎ ‎（1）写出点A、点B的坐标；‎ ‎（2）若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移，分别交线段OA、CA和抛物线于点E、M和点P，连接PA、PB．设直线l移动的时间为t（0＜t＜4）秒，求四边形PBCA的面积S（面积单位）与t（秒）的函数关系式，并求出四边形PBCA的最大面积；‎ ‎（3）在（2）的条件下，抛物线上是否存在一点P，使得△PAM是直角三角形？若存在，请求出点P的坐标；若不存在，请说明理由．‎ ‎3.（2012•海南）如图，顶点为P（4，﹣4）的二次函数图象经过原点（0，0），点A在该图象上，OA交其对称轴l于点M，点M、N关于点P对称，连接AN、ON，‎ ‎（1）求该二次函数的关系式；‎ ‎（2）若点A在对称轴l右侧的二次函数图象上运动时，请解答下面问题：‎ ‎①证明：∠ANM=∠ONM；‎ ‎②△ANO能否为直角三角形？如果能，请求出所有符合条件的点A的坐标；如果不能，请说明理由．‎ ‎4、（2012•云南）如图，在平面直角坐标系中，直线y=x+2交x轴于点P，交y轴于点A．抛物线y=x2+bx+c的图象过点E（﹣1，0），并与直线相交于A、B两点．‎ ‎（1）求抛物线的解析式（关系式）；‎ ‎（2）过点A作AC⊥AB交x轴于点C，求点C的坐标；‎ ‎（3）除点C外，在坐标轴上是否存在点M，使得△MAB是直角三角形？若存在，请求出点M的坐标；若不存在，请说明理由．‎ 二、 相似三角形与抛物线 ‎1、（2012•福州）如图1，已知抛物线y=ax2+bx（a≠0）经过A（3，0）、B（4，4）两点．‎ ‎（1）求抛物线的解析式；‎ ‎（2）将直线OB向下平移m个单位长度后，得到的直线与抛物线只有一个公共点D，求m的值及点D的坐标；‎ ‎（3）如图2，若点N在抛物线上，且∠NBO=∠ABO，则在（2）的条件下，求出所有满足△POD∽△NOB的点P坐标（点P、O、D分别与点N、O、B对应）．‎ ‎3、（2012•遵义）如图，已知抛物线y=ax2+bx+c（a≠0）的图象经过原点O，交x轴于点A，其顶点B的坐标为（3，﹣）．‎ ‎（1）求抛物线的函数解析式及点A的坐标；‎ ‎（2）在抛物线上求点P，使S△POA=2S△AOB；‎ ‎（3）在抛物线上是否存在点Q，使△AQO与△AOB相似？如果存在，请求出Q点的坐标；如果不存在，请说明理由．‎ ‎4.（2012•黄冈）如图，已知抛物线的方程C1：y=﹣（x+2）（x﹣m）（m＞0）与x轴相交于点B、C，与y轴相交于点E，且点B在点C的左侧．‎ ‎（1）若抛物线C1过点M（2，2），求实数m的值；‎ ‎（2）在（1）的条件下，求△BCE的面积；‎ ‎（3）在（1）条件下，在抛物线的对称轴上找一点H，使BH+EH最小，并求出点H的坐标；‎ ‎（4）在第四象限内，抛物线C1上是否存在点F，使得以点B、C、F为顶点的三角形与△BCE相似？若存在，求m的值；若不存在，请说明理由．‎ ‎5、（2012•常德）如图，已知二次函数的图象过点A（﹣4，3），B（4，4）．‎ ‎（1）求二次函数的解析式：‎ ‎（2）求证：△ACB是直角三角形；‎ ‎（3）若点P在第二象限，且是抛物线上的一动点，过点P作PH垂直x轴于点H，是否存在以P、H、D为顶点的三角形与△ABC相似？若存在，求出点P的坐标；若不存在，请说明理由．‎ ‎6（2012•鞍山）如图，直线AB交x轴于点B（4，0），交y轴于点A（0，4），直线DM⊥x轴正半轴于点M，交线段AB于点C，DM=6，连接DA，∠DAC=90°．‎ ‎（1）直接写出直线AB的解析式；‎ ‎（2）求点D的坐标；‎ ‎（3）若点P是线段MB上的动点，过点P作x轴的垂线，交AB于点F，交过O、D、B三点的抛物线于点E，连接CE．是否存在点P，使△BPF与△FCE相似？若存在，请求出点P的坐标；若不存在，请说明理由．‎ ‎7.（2012•阜新）在平面直角坐标系中，二次函数y=ax2+bx+2的图象与x轴交于A（﹣3，0），B（1，0）两点，与y轴交于点C．‎ ‎（1）求这个二次函数的关系解析式；‎ ‎（2）点P是直线AC上方的抛物线上一动点，是否存在点P，使△ACP的面积最大？若存在，求出点P的坐标；若不存在，说明理由；‎ 考生注意：下面的（3）、（4）、（5）题为三选一的选做题，即只能选做其中一个题目，多答时只按作答的首题评分，切记啊！‎ ‎（3）在平面直角坐标系中，是否存在点Q，使△BCQ是以BC为腰的等腰直角三角形？若存在，直接写出点Q的坐标；若不存在，说明理由；‎ ‎（4）点Q是直线AC上方的抛物线上一动点，过点Q作QE垂直于x轴，垂足为E．是否存在点Q，使以点B、Q、E为顶点的三角形与△AOC相似？若存在，直接写出点Q的坐标；若不存在，说明理由；‎ ‎（5）点M为抛物线上一动点，在x轴上是否存在点Q，使以A、C、M、Q为顶点的四边形是平行四边形？若存在，直接写出点Q的坐标；若不存在，说明理由．‎ 六、抛物线中的翻折问题 ‎1、（2012•天门）如图，抛物线y=ax2+bx+2交x轴于A（﹣1，0），B（4，0）两点，交y轴于点C，与过点C且平行于x轴的直线交于另一点D，点P是抛物线上一动点．‎ ‎（1）求抛物线解析式及点D坐标；‎ ‎（2）点E在x轴上，若以A，E，D，P为顶点的四边形是平行四边形，求此时点P的坐标；‎ ‎（3）过点P作直线CD的垂线，垂足为Q，若将△CPQ沿CP翻折，点Q的对应点为Q′．是否存在点P，使Q′恰好落在x轴上？若存在，求出此时点P的坐标；若不存在，说明理由．‎ ‎2、（2010•恩施州）如图，在平面直角坐标系中，二次函数y=x2+bx+c的图象与x轴交于A、B两点，A点在原点的左侧，B点的坐标为（3，0），与y轴交于C（0，﹣3）点，点P是直线BC下方的抛物线上一动点．‎ ‎（1）求这个二次函数的表达式．‎ ‎（2）连接PO、PC，并把△POC沿CO翻折，得到四边形POP′C，那么是否存在点P，使四边形POP′C为菱形？若存在，请求出此时点P的坐标；若不存在，请说明理由．‎ ‎（3）当点P运动到什么位置时，四边形ABPC的面积最大并求出此时P点的坐标和四边形ABPC的最大面积．‎ 动点与抛物线专题复习答案 一、平行四边形与抛物线 ‎1、解：（1）由于抛物线y=x2+bx+c与y轴交于点B（0，4），则 c=4；‎ ‎∵抛物线的对称轴 x=﹣=﹣，‎ ‎∴b=‎5a=；‎ 即抛物线的解析式：y=x2+x+4．‎ ‎（2）∵A（4，0）、B（3，0）‎ ‎∴OA=4，OB=3，AB==5；‎ 若四边形ABCD是菱形，则 BC=AD=AB=5，‎ ‎∴C（﹣5，3）、D（﹣1，0）．‎ 将C（﹣5，3）代入y=x2+x+4中，得：×（﹣5）2+×（﹣5）+4=3，所以点C在抛物线上；‎ 同理可证：点D也在抛物线上．‎ ‎（3）设直线CD的解析式为：y=kx+b，依题意，有：‎ ‎，解得 ‎ ‎∴直线CD：y=﹣x﹣．‎ 由于MN∥y轴，设 M（t，t2+t+4），则 N（t，﹣t﹣）；‎ ‎①t＜﹣5或t＞﹣1时，l=MN=（t2+t+4）﹣（﹣t﹣）=t2+t+；‎ ‎②﹣5＜t＜﹣1时，l=MN=（﹣t﹣）﹣（t2+t+4）=﹣t2﹣t﹣；‎ 若以M、N、C、E为顶点的四边形是平行四边形，由于MN∥CE，则MN=CE=3，则有：‎ t2+t+=3，解得：t=﹣3±2；‎ ‎﹣t2﹣t﹣=3，解得：t=﹣3；‎ 综上，l=‎ 且当t=﹣3±2或﹣3时，以M、N、C、E为顶点的四边形是平行四边形．‎ ‎2、解：（1）解方程x2﹣7x+12=0，得x1=3，x2=4，‎ ‎∵OA＜OB，∴OA=3，OB=4．‎ ‎∴A（0，3），B（4，0）．‎ ‎（2）在Rt△AOB中，OA=3，OB=4，∴AB=5，∴AP=t，QB=2t，AQ=5﹣2t．‎ ‎△APQ与△AOB相似，可能有两种情况：‎ ‎（I）△APQ∽△AOB，如图（2）a所示．‎ 则有，即，解得t=．‎ 此时OP=OA﹣AP=，PQ=AP•tanA=，∴Q（，）；‎ ‎（II）△APQ∽△ABO，如图（2）b所示．‎ 则有，即，解得t=．‎ 此时AQ=，AH=AQ•cosA=，HQ=AQ•sinA=，OH=OA﹣AH=，∴Q（，）．‎ 综上所述，当t=秒或t=秒时，△APQ与△AOB相似，所对应的Q点坐标分别为（，）或（，）．‎ ‎（3）结论：存在．如图（3）所示．‎ ‎∵t=2，∴AP=2，AQ=1，OP=1．‎ 过Q点作QE⊥y轴于点E，则QE=AQ•sin∠QAP=，AE=AQ•cos∠QAP=，‎ ‎∴OE=OA﹣AE=，∴Q（，）．‎ ‎∵▱APQM1，∴QM1⊥x轴，且QM1=AP=2，∴M1（，）；‎ ‎∵▱APQM2，∴QM2⊥x轴，且QM2=AP=2，∴M2（，）；‎ 如图（3），过M3点作M‎3F⊥y轴于点F，‎ ‎∵▱AQPM3，∴M3P=AQ，∠QAE=∠M3PF，∴∠PM‎3F=∠AQE；‎ 在△M3PF与△QAE中，∵∠QAE=∠M3PF，M3P=AQ，∠PM‎3F=∠AQE，‎ ‎∴△M3PF≌△QAE，‎ ‎∴M‎3F=QE=，PF=AE=，∴OF=OP+PF=，∴M3（﹣，）．‎ ‎∴当t=2时，在坐标平面内，存在点M，使以A、P、Q、M为顶点的四边形是平行四边形．‎ 点M的坐标为：M1（，），M2（，），M3（﹣，）．‎ ‎3.解：（1）由抛物线y=﹣x2+bx+c过点A（﹣1，0）及C（2，3）得，‎ ‎，‎ 解得，‎ 故抛物线为y=﹣x2+2x+3‎ 又设直线为y=kx+n过点A（﹣1，0）及C（2，3）得 ‎，‎ 解得 故直线AC为y=x+1；‎ ‎（2）作N点关于直线x=3的对称点N′，则N′（6，3），由（1）得D（1，4），‎ 故直线DN′的函数关系式为y=﹣x+，‎ 当M（3，m）在直线DN′上时，MN+MD的值最小，‎ 则m=﹣×=；‎ ‎（3）由（1）、（2）得D（1，4），B（1，2）‎ ‎∵点E在直线AC上，‎ 设E（x，x+1），‎ ‎①当点E在线段AC上时，点F在点E上方，‎ 则F（x，x+3），‎ ‎∵F在抛物线上，‎ ‎∴x+3=﹣x2+2x+3，‎ 解得，x=0或x=1（舍去）‎ ‎∴E（0，1）；‎ ‎②当点E在线段AC（或CA）延长线上时，点F在点E下方，‎ 则F（x，x﹣1）‎ 由F在抛物线上 ‎∴x﹣1=﹣x2+2x+3‎ 解得x=或x=‎ ‎∴E（，）或（，）‎ 综上，满足条件的点E为E（0，1）、（，）或（，）；‎ ‎（4）过点P作PQ⊥x轴交AC于点Q，交x轴于点H；过点C作CG⊥x轴于点G，如图2，‎ 设Q（x，x+1），则P（x，﹣x2+2x+3）‎ 又∵S△APC=S△APH+S直角梯形PHGC﹣S△AGC=（x+1）（﹣x2+2x+3）+（﹣x2+2x+3+3）（2﹣x）﹣×3×3‎ ‎=﹣x2+x+3‎ ‎=﹣（x﹣）2+‎ ‎∴△APC的面积的最大值为．‎ 二、 梯形与抛物线 ‎1、解：（1）过点C作CH⊥x轴，垂足为H；‎ ‎∵在Rt△OAB中，∠OAB=90°，∠BOA=30°，AB=2，‎ ‎∴OB=4，OA=2；‎ 由折叠的性质知：∠COB=30°，OC=AO=2，‎ ‎∴∠COH=60°，OH=，CH=3；‎ ‎∴C点坐标为（，3）．‎ ‎（2）∵抛物线y=ax2+bx（a≠0）经过C（，3）、A（2，0）两点，‎ ‎∴，‎ 解得；‎ ‎∴此抛物线的函数关系式为：y=﹣x2+2x．‎ ‎（3）存在．‎ 因为y=﹣x2+2x的顶点坐标为（，3），‎ 即为点C，MP⊥x轴，垂足为N，设PN=t；‎ 因为∠BOA=30°，‎ 所以ON=t，‎ ‎∴P（t，t）；‎ 作PQ⊥CD，垂足为Q，ME⊥CD，垂足为E；‎ 把x=t代入y=﹣x2+2x，‎ 得y=﹣3t2+6t，‎ ‎∴M（t，﹣3t2+6t），E（，﹣3t2+6t），‎ 同理：Q（，t），D（，1）；‎ 要使四边形CDPM为等腰梯形，只需CE=QD，‎ 即3﹣（﹣3t2+6t）=t﹣1，‎ 解得t=，t=1（舍），‎ ‎∴P点坐标为（，），‎ ‎∴存在满足条件的P点，使得四边形CDPM为等腰梯形，此时P点坐标为（，）．‎ ‎2、解：（1）∵抛物线y=x2+h经过点C（0，1），‎ ‎∴+h=1，‎ 解得h=1．‎ ‎（2）依题意，设抛物线y=x2+1上的点，P（a，a2+1）、Q（b，b2+1）（a＜0＜b）‎ 过点A的直线l：y=kx+2经过点P、Q，‎ ‎∴a2+1=ak+2…①‎ b2+1=bk+2…②‎ ‎①×b﹣②×a得：（a2b﹣b‎2a）+b﹣a=2（b﹣a），‎ 化简得：b=﹣；‎ ‎∴S△POQ=OA•|xQ﹣xP|=•OA•|﹣﹣a|=（﹣）+（﹣a）≥2•=4‎ 由上式知：当﹣=﹣a，即|a|=|b|（P、Q关于y轴对称）时，△POQ的面积最小；‎ 即PQ∥x轴时，△POQ的面积最小，且POQ的面积最小为4．‎ ‎（3）连接BQ，若l与x轴不平行（如图），即PQ与x轴不平行，‎ 依题意，设抛物线y=x2+1上的点，P（a，a2+1）、Q（b，b2+1）（a＜0＜b）‎ 直线BC：y=k1x+1过点P，‎ ‎∴a2+1=ak1+1，得k1=﹣a，‎ 即y=ax+1．‎ 令y=0得：xB=﹣，‎ 同理，由（2）得：b=﹣‎ ‎∴点B与Q的横坐标相同，‎ ‎∴BQ∥y轴，即BQ∥OA，‎ 又∵AQ与OB不平行，‎ ‎∴四边形AOBQ是梯形，‎ 据抛物线的对称性可得（a＞0＞b）结论相同．‎ 故在直线l旋转的过程中：当l与x轴不平行时，四边形AOBQ是梯形；当l与x轴平行时，四边形AOBQ是正方形．‎ ‎3.解：（1）由题意可知，当t=2（秒）时，OP=4，CQ=2，‎ 在Rt△PCQ中，由勾股定理得：PC===4，‎ ‎∴OC=OP+PC=4+4=8，‎ 又∵矩形AOCD，A（0，4），∴D（8，4）．‎ 点P到达终点所需时间为=4秒，点Q到达终点所需时间为=4秒，由题意可知，t的取值范围为：0＜t＜4．‎ ‎（2）结论：△AEF的面积S不变化．‎ ‎∵AOCD是矩形，∴AD∥OE，∴△AQD∽△EQC，‎ ‎∴，即，解得CE=．‎ 由翻折变换的性质可知：DF=DQ=4﹣t，则CF=CD+DF=8﹣t．‎ S=S梯形AOCF+S△FCE﹣S△AOE ‎=（OA+CF）•OC+CF•CE﹣OA•OE ‎=[4+（8﹣t）]×8+（8﹣t）•﹣×4×（8+）‎ 化简得：S=32为定值．‎ 所以△AEF的面积S不变化，S=32．‎ ‎（3）若四边形APQF是梯形，因为AP与CF不平行，所以只有PQ∥AF．‎ 由PQ∥AF可得：△CPQ∽△DAF，‎ ‎∴，即，化简得t2﹣12t+16=0，‎ 解得：t1=6+2，t2=6﹣2，‎ 由（1）可知，0＜t＜4，∴t1=6+2不符合题意，舍去．‎ ‎∴当t=（6﹣2）秒时，四边形APQF是梯形．‎ 三、等腰三角形、菱形与抛物线 ‎1、解：（1）∵点A（﹣1，0），‎ ‎∴OA=1，‎ 由图可知，∠BAC是三角板的60°角，∠ABC是30°角，‎ 所以，OC=OA•tan60°=1×=，‎ OB=OC•cot30°=×=3，‎ 所以，点B（3，0），C（0，），‎ 设抛物线解析式为y=ax2+bx+c，‎ 则，‎ 解得，‎ 所以，抛物线的解析式为y=﹣x2+x+；‎ ‎（2）①∵△OCE∽△OBC，‎ ‎∴=，‎ 即=，‎ 解得OE=1，‎ 所以，AE=OA+OE=1+1=2，‎ 即x=2时，△OCE∽△OBC；‎ ‎②存在．理由如下：‎ 抛物线的对称轴为x=﹣=﹣=1，‎ 所以，点E为抛物线的对称轴与x轴的交点，‎ ‎∵OA=OE，OC⊥x轴，∠BAC=60°，‎ ‎∴△ACE是等边三角形，‎ ‎∴∠AEC=60°，‎ 又∠DEF=60°，‎ ‎∴∠FEB=60°，‎ ‎∴∠BAC=∠FEB，‎ ‎∴EF∥AC，‎ 由A（﹣1，0），C（0，）可得直线AC的解析式为y=x+，‎ ‎∵点E（1，0），‎ ‎∴直线EF的解析式为y=x﹣，‎ 联立，‎ 解得，（舍去），‎ ‎∴点M的坐标为（2，），‎ EM==2，‎ 分三种情况讨论△PEM是等腰三角形，‎ 当PE=EM时，PE=2，‎ 所以，点P的坐标为（1，2）或（1，﹣2），‎ 当PE=PM时，∵∠FEB=60°，‎ ‎∴∠PEF=90°﹣60°=30°，‎ PE=EM÷cos30°=×2÷=，‎ 所以，点P的坐标为（1，），‎ 当PM=EM时，PE=2EM•cos30°=2×2×=2，‎ 所以，点P的坐标为（1，2），‎ 综上所述，抛物线对称轴上存在点P（1，2）或（1，﹣2）或（1，）或（1，2），使△PEM是等腰三角形．‎ ‎3、解：（1）由题意，A（6，0）、B（0，8），则OA=6，OB=8，AB=10；‎ 当t=3时，AN=t=5=AB，即N是线段AB的中点；‎ ‎∴N（3，4）．‎ 设抛物线的解析式为：y=ax（x﹣6），则：‎ ‎4=‎3a（3﹣6），a=﹣；‎ ‎∴抛物线的解析式：y=﹣x（x﹣6）=﹣x2+x．‎ ‎（2）过点N作NC⊥OA于C；‎ 由题意，AN=t，AM=OA﹣OM=6﹣t，NC=NA•sin∠BAO=t•=t；‎ 则：S△MNA=AM•NC=×（6﹣t）×t=﹣（t﹣3）2+6．‎ ‎∴△MNA的面积有最大值，且最大值为6．‎ ‎（3）Rt△NCA中，AN=t，NC=AN•sin∠BAO=t，AC=AN•cos∠BAO=t；‎ ‎∴OC=OA﹣AC=6﹣t，∴N（6﹣t，t）．‎ ‎∴NM==；‎ 又：AM=6﹣t，AN=t（0＜t＜6）；‎ ‎①当MN=AN时，=t，即：t2﹣8t+12=0，t1=2，t2=6（舍去）；‎ ‎②当MN=MA时，=6﹣t，即：t2﹣12t=0，t1=0（舍去），t2=；‎ ‎③当AM=AN时，6﹣t=t，即t=；‎ 综上，当t的值取 2或或 时，△MAN是等腰三角形．‎ ‎4、解：（1）抛物线y=ax2+bx+c（a≠0）经过A（﹣1，0），B（3，0），C（0，）三点，‎ ‎∴，解得a=，b=，c=，‎ ‎∴抛物线的解析式为：y=x2x．‎ ‎（2）设直线l1的解析式为y=kx+b，由题意可知，直线l1经过A（﹣1，0），C（0，）两点，‎ ‎∴，解得k=，b=，∴直线l1的解析式为：y=x；‎ 直线l2经过B（3，0），C（0，）两点，同理可求得直线l2解析式为：y=x．‎ ‎∵抛物线y=x2x=（x﹣1）2，‎ ‎∴对称轴为x=1，D（1，0），顶点坐标为F（1，）；‎ 点E为x=1与直线l2：y=x的交点，令x=1，得y=，∴E（1，）；‎ 点G为x=1与直线l1：y=x的交点，令x=1，得y=，∴G（1，）．‎ ‎∴各点坐标为：D（1，0），E（1，），F（1，），G（1，），它们均位于对称轴x=1上，‎ ‎∴DE=EF=FG=．‎ ‎（3）如右图，过C点作C关于对称轴x=1的对称点P1，CP1交对称轴于H点，连接CF．‎ ‎△PCG为等腰三角形，有三种情况：‎ ‎①当CG=PG时，如右图，由抛物线的对称性可知，此时P1满足P‎1G=CG．‎ ‎∵C（0，），对称轴x=1，∴P1（2，）．‎ ‎②当CG=PC时，此时P点在抛物线上，且CP的长度等于CG．‎ 如右图，C（1，），H点在x=1上，∴H（1，），‎ 在Rt△CHG中，CH=1，HG=|yG﹣yH|=|﹣（）|=，‎ ‎∴由勾股定理得：CG==2．‎ ‎∴PC=2．‎ 如右图，CP1=2，此时与①中情形重合；‎ 又Rt△OAC中，AC==2，∴点A满足PC=2的条件，但点A、C、G在同一条直线上，所以不能构成等腰三角形．‎ ‎③当PC=PG时，此时P点位于线段CG的垂直平分线上．‎ ‎∵l1⊥l2，∴△ECG为直角三角形，‎ 由（2）可知，EF=FG，即F为斜边EG的中点，‎ ‎∴CF=FG，∴F为满足条件的P点，∴P2（1，）；‎ 又cos∠CGE==，∴∠CGE=30°，∴∠HCG=60°，‎ 又P‎1C=CG，∴△P1CG为等边三角形，‎ ‎∴P1点也在CG的垂直平分线上，此种情形与①重合．‎ 综上所述，P点的坐标为P1（2，）或P2（1，）．‎ ‎5、解：（1）过点B作BF⊥x轴于F 在Rt△BCF中 ‎∵∠BCO=45°，BC=6‎ ‎∴CF=BF=12 ‎ ‎∵C 的坐标为（﹣18，0）‎ ‎∴AB=OF=6‎ ‎∴点B的坐标为（﹣6，12）．‎ ‎（2）过点D作DG⊥y轴于点G ‎∵AB∥DG ‎∴△ODG∽△OBA ‎ ‎∵===，AB=6，OA=12‎ ‎∴DG=4，OG=8 ‎ ‎∴D（﹣4，8），E（0，4）‎ 设直线DE解析式为y=kx+b（k≠0）‎ ‎∴‎ ‎∴‎ ‎∴直线DE解析式为y=﹣x+4．‎ ‎（3）结论：存在．‎ 设直线y=﹣x+4分别与x轴、y轴交于点E、点F，则E（0，4），F（4，0），OE=OF=4，EF=4．‎ 如答图2所示，有四个菱形满足题意．‎ ‎①菱形OEP1Q1，此时OE为菱形一边．‎ 则有P1E=P1Q1=OE=4，P‎1F=EF﹣P1E=4﹣4．‎ 易知△P1NF为等腰直角三角形，∴P1N=NF=P‎1F=4﹣2；‎ 设P1Q1交x轴于点N，则NQ1=P1Q1﹣P1N=4﹣（4﹣2）=2，‎ 又ON=OF﹣NF=2，∴Q1（2，﹣2）；‎ ‎②菱形OEP2Q2，此时OE为菱形一边．‎ 此时Q2与Q1关于原点对称，∴Q2（﹣2，2）；‎ ‎③菱形OEQ3P3，此时OE为菱形一边．‎ 此时P3与点F重合，菱形OEQ3P3为正方形，∴Q3（4，4）；‎ ‎④菱形OP4EQ4，此时OE为菱形对角线．‎ 由菱形性质可知，P4Q4为OE的垂直平分线，‎ 由OE=4，得P4纵坐标为2，代入直线解析式y=﹣x+4得横坐标为2，则P4（2，2），‎ 由菱形性质可知，P4、Q4关于OE或x轴对称，∴Q4（﹣2，2）．‎ 综上所述，存在点Q，使以O、E、P、Q为顶点的四边形是菱形；‎ 点Q的坐标为：Q1（2，﹣2），Q2（﹣2，2），Q3（4，4），Q4（﹣2，2）．‎ ‎6、解：（1）∵点B（﹣2，m）在直线y=﹣2x﹣1上 ‎∴m=3 即B（﹣2，3）‎ 又∵抛物线经过原点O ‎∴设抛物线的解析式为y=ax2+bx ‎∵点B（﹣2，3），A（4，0）在抛物线上 ‎∴，‎ 解得：．‎ ‎∴设抛物线的解析式为．‎ ‎（2）∵P（x，y）是抛物线上的一点，‎ ‎∴，‎ 若S△ADP=S△ADC，‎ ‎∵，，‎ 又∵点C是直线y=﹣2x﹣1与y轴交点，‎ ‎∴C（0，1），‎ ‎∴OC=1，‎ ‎∴，即或，‎ 解得：．‎ ‎∴点P的坐标为 ．‎ ‎（3）结论：存在．‎ ‎∵抛物线的解析式为，‎ ‎∴顶点E（2，﹣1），对称轴为x=2；‎ 点F是直线y=﹣2x﹣1与对称轴x=2的交点，∴F（2，﹣5），DF=5．‎ 又∵A（4，0），‎ ‎∴AE=．‎ 如右图所示，在点M的运动过程中，依次出现四个菱形：‎ ‎①菱形AEM1Q1．‎ ‎∵此时DM1=AE=，‎ ‎∴M‎1F=DF﹣DE﹣DM1=4﹣，‎ ‎∴t1=4﹣；‎ ‎②菱形AEOM2．‎ ‎∵此时DM2=DE=1，‎ ‎∴M‎2F=DF+DM2=6，‎ ‎∴t2=6；‎ ‎③菱形AEM3Q3．‎ ‎∵此时EM3=AE=，‎ ‎∴DM3=EM3﹣DE=﹣1，‎ ‎∴M‎3F=DM3+DF=（﹣1）+5=4+，‎ ‎∴t3=4+；‎ ‎④菱形AM4EQ4．‎ 此时AE为菱形的对角线，设对角线AE与M4Q4交于点H，则AE⊥M4Q4，‎ ‎∵易知△AED∽△M4EH，‎ ‎∴，即，得M4E=，‎ ‎∴DM4=M4E﹣DE=﹣1=，‎ ‎∴M‎4F=DM4+DF=+5=，∴t4=．‎ 综上所述，存在点M、点Q，使得以Q、A、E、M四点为顶点的四边形是菱形；时间t的值为：t1=4﹣，t2=6，t3=4+，t4=．‎ 四、直角三角形与抛物线 ‎1、解：（1）令y=0，即=0，‎ 解得x1=﹣4，x2=2，‎ ‎∴A、B点的坐标为A（﹣4，0）、B（2，0）．‎ ‎（2）S△ACB=AB•OC=9，‎ 在Rt△AOC中，AC===5，‎ 设△ACD中AC边上的高为h，则有AC•h=9，解得h=．‎ 如答图1，在坐标平面内作直线平行于AC，且到AC的距离=h=，这样的直线有2条，分别是l1和l2，则直线与对称轴x=﹣1的两个交点即为所求的点D．‎ 设l1交y轴于E，过C作CF⊥l1于F，则CF=h=，‎ ‎∴CE==．‎ 设直线AC的解析式为y=kx+b，将A（﹣4，0），B（0，3）坐标代入，‎ 得到，解得，∴直线AC解析式为y=x+3．‎ 直线l1可以看做直线AC向下平移CE长度单位（个长度单位）而形成的，‎ ‎∴直线l1的解析式为y=x+3﹣=x﹣．‎ 则D1的纵坐标为×（﹣1）﹣=，∴D1（﹣4，）．‎ 同理，直线AC向上平移个长度单位得到l2，可求得D2（﹣1，）‎ 综上所述，D点坐标为：D1（﹣4，），D2（﹣1，）．‎ ‎（3）如答图2，以AB为直径作⊙F，圆心为F．过E点作⊙F的切线，这样的切线有2条．‎ 连接FM，过M作MN⊥x轴于点N．‎ ‎∵A（﹣4，0），B（2，0），∴F（﹣1，0），⊙F半径FM=FB=3．‎ 又FE=5，则在Rt△MEF中，‎ ME==4，sin∠MFE=，cos∠MFE=．‎ 在Rt△FMN中，MN=MN•sin∠MFE=3×=，‎ FN=MN•cos∠MFE=3×=，则ON=，‎ ‎∴M点坐标为（，）‎ 直线l过M（，），E（4，0），‎ 设直线l的解析式为y=kx+b，则有 ‎，解得，‎ 所以直线l的解析式为y=x+3．‎ 同理，可以求得另一条切线的解析式为y=x﹣3．‎ 综上所述，直线l的解析式为y=x+3或y=x﹣3．‎ ‎2、解：（1）抛物线y=﹣x2+x+4中：‎ 令x=0，y=4，则 B（0，4）；‎ 令y=0，0=﹣x2+x+4，解得 x1=﹣1、x2=8，则 A（8，0）；‎ ‎∴A（8，0）、B（0，4）．‎ ‎（2）△ABC中，AB=AC，AO⊥BC，则OB=OC=4，∴C（0，﹣4）．‎ 由A（8，0）、B（0，4），得：直线AC：y=﹣x+4；‎ 依题意，知：OE=2t，即 E（2t，0）；‎ ‎∴P（2t，﹣2t2+7t+4）、Q（2t，﹣t+4），PQ=（﹣2t2+7t+4）﹣（﹣t+4）=﹣2t2+8t；‎ S=S△ABC+S△PAB=×8×8+×（﹣2t2+8t）×8=﹣8t2+32t+32=﹣8（t﹣2）2+64；‎ ‎∴当t=2时，S有最大值，且最大值为64．‎ ‎（3）∵PM∥y轴，∴∠AMP=∠ACO＜90°；‎ 而∠APM是锐角，所以△PAM若是直角三角形，只能是∠PAM=90°；‎ 由A（8，0）、C（0，﹣4），得：直线AC：y=x﹣4；‎ 所以，直线AP可设为：y=﹣2x+h，代入A（8，0），得：‎ ‎﹣16+h=0，h=16‎ ‎∴直线AP：y=﹣2x+16，联立抛物线的解析式，得：‎ ‎，解得 、‎ ‎∴存在符合条件的点P，且坐标为（3，10）．‎ ‎3.解：（1）∵二次函数的顶点坐标为（4，﹣4），‎ ‎∴设二次函数的解析式为y=a（x﹣4）2﹣4，‎ 又二次函数过（0，0），‎ ‎∴0=a（0﹣4）2﹣4，解得：a=，‎ ‎∴二次函数解析式为y=（x﹣4）2﹣4=x2﹣2x；‎ ‎（2）①证明：过A作AH⊥l于H，l与x轴交于点D，如图所示：‎ 设A（m，m2﹣‎2m），又O（0，0），‎ ‎∴直线AO的解析式为y=x=（m﹣2）x，‎ 则M（4，m﹣8），N（4，﹣m），H（4，m2﹣‎2m），‎ ‎∴OD=4，ND=m，HA=m﹣4，NH=ND﹣HD=m2﹣m，‎ 在Rt△OND中，tan∠ONM==，‎ 在Rt△ANH中，tan∠ANM====，‎ ‎∴tan∠ONM=tan∠ANM，‎ 则∠ANM=∠ONM；‎ ‎②△ANO不能为直角三角形，理由如下：‎ 分三种情况考虑：‎ ‎（i）若∠ONA为直角，由①得：∠ANM=∠ONM=45°，‎ ‎∴△AHN为等腰直角三角形，‎ ‎∴HA=NH，即m﹣4=m2﹣m，‎ 整理得：m2﹣‎8m+16=0，即（m﹣4）2=0，‎ 解得：m=4，‎ 此时点A与点P重合，故不存在A点使△ONA为直角三角形；‎ ‎（ii）若∠AON为直角，根据勾股定理得：OA2+ON2=AN2，‎ ‎∵OA2=m2+（m2﹣‎2m）2，ON2=42+m2，AN2=（m﹣4）2+（m2﹣‎2m+m）2，‎ ‎∴m2+（m2﹣‎2m）2+42+m2=（m﹣4）2+（m2﹣‎2m+m）2，‎ 整理得：m（m﹣4）2=0，‎ 解得：m=0或m=4，‎ 此时A点与P点重合或与原点重合，故∠AON不能为直角；‎ ‎（iii）若∠NAO为直角，可得∠NAM=∠ODM=90°，且∠AMN=∠DMO，‎ ‎∴△AMN∽△DMO，‎ 又∠MAN=∠ODN=90°，且∠ANM=∠OND，‎ ‎∴△AMN∽△DON，‎ ‎∴△AMN∽△DMO∽△DON，‎ ‎∴=，即=，‎ 整理得：（m﹣4）2=0，‎ 解得：m=4，‎ 此时A与P重合，故∠NAO不能为直角，‎ 综上，点A在对称轴l右侧的二次函数图象上运动时，△ANO不能为直角三角形 ‎4、‎ 解：（1）直线解析式为y=x+2，令x=0，则y=2，‎ ‎∴A（0，2），‎ ‎∵抛物线y=x2+bx+c的图象过点A（0，2），E（﹣1，0），‎ ‎∴，‎ 解得．‎ ‎∴抛物线的解析式为：y=x2+x+2． ‎ ‎（2）∵直线y=x+2分别交x轴、y轴于点P、点A，‎ ‎∴P（6，0），A（0，2），‎ ‎∴OP=6，OA=2．‎ ‎∵AC⊥AB，OA⊥OP，‎ ‎∴Rt△OCA∽Rt△OPA，∴，‎ ‎∴OC=，‎ 又C点在x轴负半轴上，‎ ‎∴点C的坐标为C（，0）．‎ ‎（3）抛物线y=x2+x+2与直线y=x+2交于A、B两点，‎ 令x2+x+2=x+2，‎ 解得x1=0，x2=，‎ ‎∴B（，）．‎ 如答图①所示，过点B作BD⊥x轴于点D，‎ 则D（，0），BD=，DP=6﹣=．‎ 点M在坐标轴上，且△MAB是直角三角形，有以下几种情况：‎ ‎①当点M在x轴上，且BM⊥AB，如答图①所示．‎ 设M（m，0），则MD=﹣m．‎ ‎∵BM⊥AB，BD⊥x轴，∴，‎ 即，‎ 解得m=，‎ ‎∴此时M点坐标为（，0）；‎ ‎②当点M在x轴上，且BM⊥AM，如答图①所示．‎ 设M（m，0），则MD=﹣m．‎ ‎∵BM⊥AM，易知Rt△AOM∽Rt△MDB，‎ ‎∴，即，‎ 化简得：m2﹣m+=0，‎ 解得：x1=，x2=，‎ ‎∴此时M点坐标为（，0），（，0）；‎ ‎（说明：此时的M点相当于以AB为直径的圆与x轴的两个交点）‎ ‎③当点M在y轴上，且BM⊥AM，如答图②所示．‎ 此时M点坐标为（0，）；‎ ‎④当点M在y轴上，且BM′⊥AB，如答图②所示．‎ 设M′（0，m），则AM=2﹣=，BM=，MM′=﹣m．‎ 易知Rt△ABM∽Rt△MBM′，‎ ‎∴，即，‎ 解得m=，‎ ‎∴此时M点坐标为（0，）．‎ 综上所述，除点C外，在坐标轴上存在点M，使得△MAB是直角三角形．‎ 符合条件的点M有5个，其坐标分别为：（，0）、（，0）、（，0）、（0，）或（0，）．‎ 五、相似三角形与抛物线 ‎1、解：（1）∵抛物线y=y=ax2+bx（a≠0）经过A（3，0）、B（4，4）‎ ‎∴，解得：‎ ‎∴抛物线的解析式是y=x2﹣3x．‎ ‎（2）设直线OB的解析式为y=k1x，由点B（4，4），‎ 得：4=4k1，解得：k1=1‎ ‎∴直线OB的解析式为y=x，‎ ‎∴直线OB向下平移m个单位长度后的解析式为：y=x﹣m，‎ ‎∵点D在抛物线y=x2﹣3x上，‎ ‎∴可设D（x，x2﹣3x），‎ 又点D在直线y=x﹣m上，‎ ‎∴x2﹣3x=x﹣m，即x2﹣4x+m=0，‎ ‎∵抛物线与直线只有一个公共点，‎ ‎∴△=16﹣‎4m=0，‎ 解得：m=4，‎ 此时x1=x2=2，y=x2﹣3x=﹣2，‎ ‎∴D点的坐标为（2，﹣2）．‎ ‎（3）∵直线OB的解析式为y=x，且A（3，0），‎ ‎∴点A关于直线OB的对称点A′的坐标是（0，3），‎ 设直线A′B的解析式为y=k2x+3，过点（4，4），‎ ‎∴4k2+3=4，解得：k2=，‎ ‎∴直线A′B的解析式是y=，‎ ‎∵∠NBO=∠ABO，‎ ‎∴点N在直线A′B上，‎ ‎∴设点N（n，），又点N在抛物线y=x2﹣3x上，‎ ‎∴=n2﹣3n，‎ 解得：n1=﹣，n2=4（不合题意，舍去）‎ ‎∴N点的坐标为（﹣，）．‎ 方法一：‎ 如图1，将△NOB沿x轴翻折，得到△N1OB1，‎ 则N1（，），B1（4，﹣4），‎ ‎∴O、D、B1都在直线y=﹣x上．‎ ‎∵△P1OD∽△NOB，‎ ‎∴△P1OD∽△N1OB1，‎ ‎∴，‎ ‎∴点P1的坐标为（，）．‎ 将△OP1D沿直线y=﹣x翻折，可得另一个满足条件的点P2（，），‎ 综上所述，点P的坐标是（，）或（，）．‎ ‎2、解：（1）设函数解析式为：y=ax2+bx+c，‎ 由函数经过点A（﹣4，0）、B（1，0）、C（﹣2，6），‎ 可得，‎ 解得：，‎ 故经过A、B、C三点的抛物线解析式为：y=﹣x2﹣3x+4；‎ ‎（2）设直线BC的函数解析式为y=kx+b，‎ 由题意得：，‎ 解得：，‎ 即直线BC的解析式为y=﹣2x+2．‎ 故可得点E的坐标为（0，2），‎ 从而可得：AE==2，CE==2，‎ 故可得出AE=CE；‎ ‎（3）相似．理由如下：‎ 设直线AD的解析式为y=kx+b，‎ 则，‎ 解得：，‎ 即直线AD的解析式为y=x+4．‎ 联立直线AD与直线BC的函数解析式可得：，‎ 解得：，‎ 即点F的坐标为（﹣，），‎ 则BF==，AF==，‎ 又∵AB=5，BC==3，‎ ‎∴=，=，‎ ‎∴=，‎ 又∵∠ABF=∠CBA，‎ ‎∴△ABF∽△CBA．‎ 故以A、B、F为顶点的三角形与△ABC相似．‎ ‎3、解：（1）由函数图象经过原点得，函数解析式为y=ax2+bx（a≠0），‎ 又∵函数的顶点坐标为（3，﹣），‎ ‎∴，‎ 解得：，‎ 故函数解析式为：y=x2﹣x，‎ 由二次函数图象的对称性可得点A的坐标为（6，0）；‎ ‎（2）∵S△POA=2S△AOB，‎ ‎∴点P到OA的距离是点B到OA距离的2倍，即点P的纵坐标为2，‎ 代入函数解析式得：2=x2﹣x，‎ 解得：x1=3+，x2=3﹣，‎ 即可得满足条件的有两个，P1（3+，2），P2（3﹣，2）．‎ ‎（3）存在．‎ 过点B作BP⊥OA，则tan∠BAP==，‎ 故可得∠BOA=60°，‎ 设Q1坐标为（x，x2﹣x），过点Q1作Q‎1F⊥x轴，‎ ‎∵△OAB∽△OQ‎1A，‎ ‎∴∠Q1OA=30°，‎ 故可得OF=Q‎1F，即x=（x2﹣x），‎ 解得：x=9或x=0（舍去），‎ 即可得Q1坐标为（9，3），‎ 根据函数的对称性可得Q2坐标为（﹣3，3）．‎ ‎4.解：（1）依题意，将M（2，2）代入抛物线解析式得：‎ ‎2=﹣（2+2）（2﹣m），解得m=4．‎ ‎（2）令y=0，即（x+2）（x﹣4）=0，解得x1=﹣2，x2=4，‎ ‎∴B（﹣2，0），C（4，0）‎ 在C1中，令x=0，得y=2，∴E（0，2）．‎ ‎∴S△BCE=BC•OE=6．‎ ‎（3）当m=4时，易得对称轴为x=1，又点B、C关于x=1对称．‎ 如答图1，连接BC，交x=1于H点，此时BH+CH最小（最小值为线段CE的长度）．‎ 设直线EC：y=kx+b，将E（0，2）、C（4，0）代入得：y=x+2，‎ 当x=1时，y=，∴H（1，）．‎ ‎（4）分两种情形讨论：‎ ‎①当△BEC∽△BCF时，如答图2所示．‎ 则，∴BC2=BE•BF．‎ 由（2）知B（﹣2，0），E（0，2），即OB=OB，∴∠EBC=45°，∴∠CBF=45°，‎ 作FT⊥x轴于点F，则BT=TF．‎ ‎∴可令F（x，﹣x﹣2）（x＞0），又点F在抛物线上，‎ ‎∴﹣x﹣2=﹣（x+2）（x﹣m），∵x+2＞0（∵x＞0），‎ ‎∴x=‎2m，F（‎2m，﹣‎2m﹣2）．‎ 此时BF==（m+1），BE=，BC=m+2，‎ 又BC2=BE•BF，∴（m+1）2=•（m+1），‎ ‎∴m=2±，‎ ‎∵m＞0，∴m=+2．‎ ‎②当△BEC∽△FCB时，如答图3所示．‎ 则，∴BC2=EC•BF．‎ 同①，∵∠EBC=∠CFB，△BTF∽△COE，，‎ ‎∴可令F（x，（x+2））（x＞0）‎ 又点F在抛物线上，∴（x+2）=﹣（x+2）（x﹣m），‎ ‎∵x+2＞0（∵x＞0），‎ ‎∴x=m+2，∴F（m+2，（m+2）），EC=，BC=m+2，‎ 又BC2=EC•BF，∴（m+2）2=•‎ 整理得：0=16，显然不成立．‎ 综合①②得，在第四象限内，抛物线上存在点F，使得以点B、C、F为顶点的三角形与△BCE相似，m=+2．‎ ‎5、解：（1）由题意得，函数图象经过点A（﹣4，3），B（4，4），‎ 故可得：，‎ 解得：，‎ 故二次函数关系式为：y=（x+2）（13x﹣20）．‎ ‎（2）由（1）所求函数关系式可得点C坐标为（﹣2，0），点D坐标为（，0），‎ 又∵点A（﹣4，3），B（4，4），‎ ‎∴AB==，AC==，BC==，‎ ‎∵满足AB2=AC2+BC2，‎ ‎∴△ACB是直角三角形．‎ ‎（3）存在点P的坐标，点P的坐标为（﹣，）或（﹣，）．‎ 设点P坐标为（x，（x+2）（13x﹣20）），则PH=（x+2）（13x﹣20），HD=﹣x+，‎ ‎①若△DHP∽△BCA，则=，即=，‎ 解得：x=﹣或x=（因为点P在第二象限，故舍去）；‎ 代入可得PH=，即P1坐标为（﹣，）；‎ ‎②若△PHD∽△BCA，则=，即=，‎ 解得：x=﹣或x=（因为点P在第二象限，故舍去）．‎ 代入可得PH=，即P2坐标为：（﹣，）．‎ 综上所述，满足条件的点P有两个，即P1（﹣，）、P2（﹣，）．‎ ‎6、解：（1）设直线AB的解析式为y=kx+b，将A（0，4），B（4，0）两点坐标代入，‎ 得，解得，所以，直线AB的解析式为y=﹣x+4；‎ ‎（2）过D点作DG⊥y轴，垂足为G，‎ ‎∵OA=OB=4，∴△OAB为等腰直角三角形，‎ 又∵AD⊥AB，∴∠DAG=90°﹣∠OAB=45°，即△ADG为等腰直角三角形，‎ ‎∴DG=AG=OG﹣OA=DM﹣OA=5﹣4=2，∴D（2，6）；‎ ‎（3）存在．‎ 由抛物线过O（0，0），B（4，0）两点，设抛物线解析式为y=ax（x﹣4），‎ 将D（2，6）代入，得a=﹣，所以，抛物线解析式为y=﹣x（x﹣4），‎ 由（2）可知，∠B=45°，则∠CFE=∠BFP=45°，C（2，2），‎ 设P（x，0），则MP=x﹣2，PB=4﹣x，‎ ‎①当∠ECF=∠BPF=90°时（如图1），△BPF与△FCE相似，‎ 过C点作CH⊥EF，此时，△CHE、△CHF、△PBF为等腰直角三角形，‎ 则PE=PF+FH+EH=PB+2MP=4﹣x+2（x﹣2）=x，‎ 将E（x，x）代入抛物线y=﹣x（x﹣4）中，得x=﹣x（x﹣4），解得x=0或，即P（，0），‎ ‎②当∠CEF=∠BPF=90°时（如图2），此时，△CEF、△BPF为等腰直角三角形，‎ 则PE=MC=2，将E（x，2）代入抛物线y=﹣x（x﹣4）中，得2=﹣x（x﹣4），‎ 解得x=或，即P（，0），‎ 所以，P（，0）或（，0）．‎ ‎7.解：（1）由抛物线y=ax2+bx+2过点A（﹣3，0），B（1，0），则 解这个方程组，得a=﹣，b=﹣．‎ ‎∴二次函数的关系解析式为y=﹣x2﹣x+2．‎ ‎（2）设点P坐标为（m，n），则n=﹣m2﹣m+2．‎ 连接PO，作PM⊥x轴于M，PN⊥y轴于N．‎ PM=﹣m2﹣m+2，PN=﹣m，AO=3．‎ 当x=0时，y=﹣×0﹣×0+2=2，所以OC=2‎ S△PAC=S△PAO+S△PCO﹣S△ACO=AO•PM+CO•PN﹣AO•CO ‎=×3•（﹣m2﹣m+2）+×2•（﹣m）﹣×3×2‎ ‎=﹣m2﹣‎‎3m ‎∵a=﹣1＜0‎ ‎∴函数S△PAC=﹣m2﹣‎3m有最大值 当m=﹣=﹣时，S△PAC有最大值．‎ 此时n=﹣m2﹣m+2=﹣﹣+2=‎ ‎∴存在点P（﹣，），使△PAC的面积最大．‎ ‎（3）如图（3）所示，以BC为边在两侧作正方形BCQ1Q2、正方形BCQ4Q3，则点Q1，Q2，Q3，Q4为符合题意要求的点．‎ 过Q1点作Q1D⊥y轴于点D，易证△Q1CD≌△CBO，‎ ‎∴Q1D=OC=2，CD=OB=1，∴OD=OC+CD=3，∴Q1（2，3）；‎ 同理求得Q2（3，1），Q3（﹣1，﹣1），Q4（﹣2，1）．‎ ‎∴存在点Q，使△BCQ是以BC为腰的等腰直角三角形．Q点坐标为：Q1（2，3），Q2（3，1），Q3（﹣1，﹣1），Q4（﹣2，1）．‎ ‎（4）如图（4）所示，设E（n，0），则BE=1﹣n，QE=﹣n2﹣n+2．‎ 假设以点B、Q、E为顶点的三角形与△AOC相似，则有两种情况：‎ ‎①若△AOC∽△BEQ，则有：，‎ 即，化简得：n2+n﹣2=0，‎ 解得n1=﹣2，n2=1（与B重合，舍去），∴n=﹣2，QE=﹣n2﹣n+2=2．‎ ‎∴Q（﹣2，2）；‎ ‎②若△AOC∽△BQE，则有：，‎ 即，化简得：4n2﹣n﹣3=0，‎ 解得n1=﹣，n2=1（与B重合，舍去），∴n=﹣，QE=﹣n2﹣n+2=．‎ ‎∴Q（﹣，）．‎ 综上所述，存在点Q，使以点B、Q、E为顶点的三角形与△AOC相似．‎ Q点坐标为（﹣2，2）或（﹣，）．‎ ‎（5）假设存在点Q，使以A、C、M、Q为顶点的四边形是平行四边形．‎ ‎①若CM平行于x轴，如图（5）a所示，有符合要求的两个点Q1，Q2，此时Q‎1A=Q‎2A=CM．‎ ‎∵CM∥x轴，∴点M、点C（0，2）关于对称轴x=﹣1对称，‎ ‎∴M（﹣2，2），∴CM=2．‎ 由Q‎1A=Q‎2A=CM=2，得到Q1（﹣5，0），Q2（﹣1，0）；‎ ‎②若CM不平行于x轴，如图（5）b所示．过点M作MG⊥x轴于G，‎ 易证△MGQ≌△COA，得QG=OA=3，MG=OC=2，即yM=﹣2．‎ 设M（x，﹣2），则有﹣x2﹣x+2=﹣2，解得x=﹣1±．‎ 又QG=3，∴xQ=xG+3=2±，‎ ‎∴Q3（2+，0），Q4（2﹣，0）．‎ 综上所述，存在点Q，使以A、C、M、Q为顶点的四边形是平行四边形．Q点坐标为：Q1（﹣5，0），Q2（﹣1，0），Q3（2+，0），Q4（2﹣，0）．‎ 六、抛物线中的翻折问题 ‎1、解：（1）∵抛物线y=ax2+bx+2经过A（﹣1，0），B（4，0）两点，‎ ‎∴，‎ 解得：‎ ‎∴y=﹣x2+x+2；‎ 当y=2时，﹣x2+x+2=2，解得：x1=3，x2=0（舍），‎ 即：点D坐标为（3，2）．‎ ‎（2）A，E两点都在x轴上，AE有两种可能：‎ ‎①当AE为一边时，AE∥PD，‎ ‎∴P1（0，2），‎ ‎②当AE为对角线时，根据平行四边形对顶点到另一条对角线距离相等，‎ 可知P点、D点到直线AE（即x轴）的距离相等，‎ ‎∴P点的纵坐标为﹣2，‎ 代入抛物线的解析式：﹣x2+x+2=﹣2‎ 解得：x1=，x2=，‎ ‎∴P点的坐标为（，﹣2），（，﹣2）‎ 综上所述：p1（0，2）；p2（，﹣2）；p3（，﹣2）．‎ ‎（3）存在满足条件的点P，显然点P在直线CD下方，设直线PQ交x轴于F，点P的坐标为（a，﹣a2+a+2），‎ ‎①当P点在y轴右侧时（如图1），CQ=a，‎ PQ=2﹣（﹣a2+a+2）=a2﹣a，‎ 又∵∠CQ′O+∠FQ′P=90°，∠COQ′=∠Q′FP=90°，‎ ‎∴∠FQ′P=∠OCQ′，‎ ‎∴△COQ′～△Q′FP，，，‎ ‎∴Q′F=a﹣3，‎ ‎∴OQ′=OF﹣Q′F=a﹣（a﹣3）=3，CQ=CQ′==，‎ 此时a=，点P的坐标为（，），‎ ‎②当P点在y轴左侧时（如图2）此时a＜0，，﹣a2+a+2＜0，CQ=﹣a，‎ PQ=2﹣（﹣a2+a+2）=a2﹣a，‎ 又∵∠CQ′O+∠FQ′P=90°，∠CQ′O+∠OCQ′=90°，‎ ‎∴∠FQ′P=∠OCQ′，∠COQ′=∠Q′FP=90°，‎ ‎∴△COQ′～△Q′FP，，，Q′F=3﹣a，‎ ‎∴OQ′=3，‎ CQ=CQ′=，‎ 此时a=﹣，点P的坐标为（﹣，）．‎ 综上所述，满足条件的点P坐标为（，），（﹣，）．‎ ‎2、解：（1）将B、C两点的坐标代入得（2分）‎ 解得：；‎ 所以二次函数的表达式为：‎ y=x2﹣2x﹣3（3分）‎ ‎（2）存在点P，使四边形POPC为菱形；‎ 设P点坐标为（x，x2﹣2x﹣3），PP′交CO于E 若四边形POP′C是菱形，则有PC=PO；‎ 连接PP′，则PE⊥CO于E，‎ ‎∴OE=EC=‎ ‎∴y=；（6分）‎ ‎∴x2﹣2x﹣3=‎ 解得x1=，x2=（不合题意，舍去）‎ ‎∴P点的坐标为（，）（8分）‎ ‎（3）过点P作y轴的平行线与BC交于点Q，与OB交于点F，设P（x，x2﹣2x﹣3），‎ 易得，直线BC的解析式为y=x﹣3‎ 则Q点的坐标为（x，x﹣3）；‎ S四边形ABPC=S△ABC+S△BPQ+S△CPQ ‎=AB•OC+QP•OF+QP•BF ‎=‎ ‎=（10分）‎ 当时，四边形ABPC的面积最大 此时P点的坐标为，四边形ABPC的面积的最大值为．（12分）‎