2017河北中考数学试卷黑白卷白卷及答案

2017河北中考数学试卷黑白卷白卷及答案

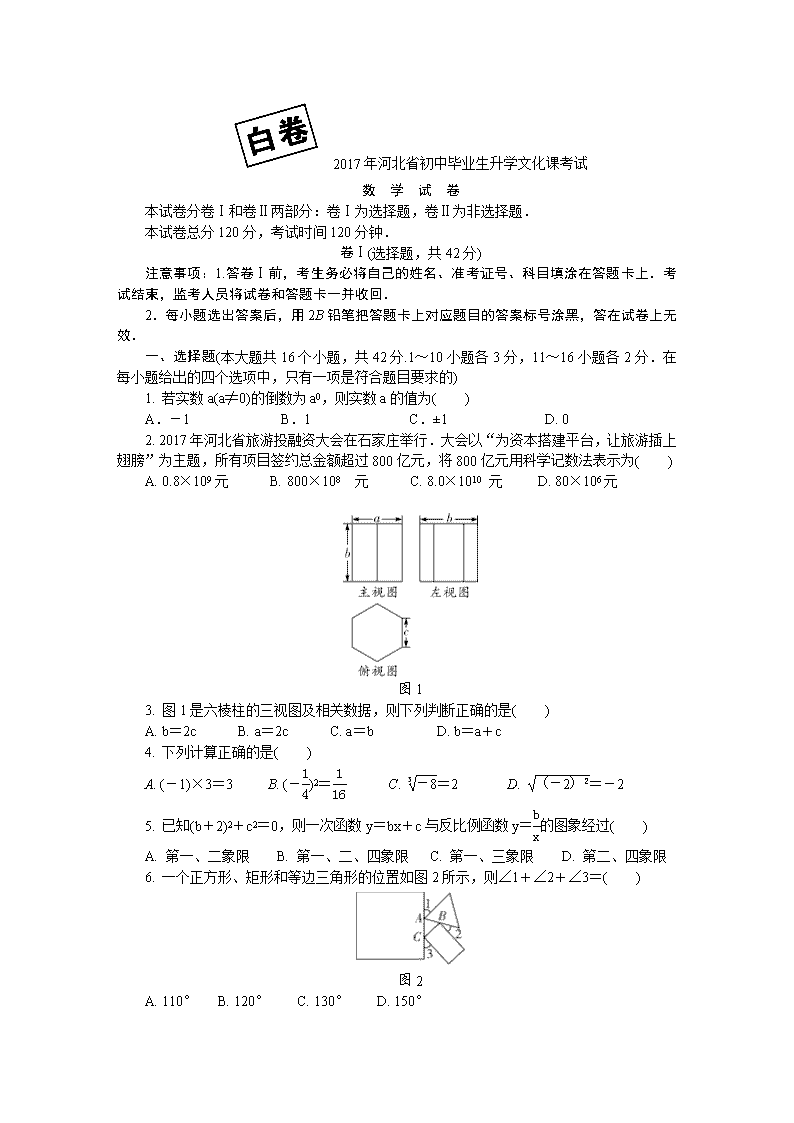
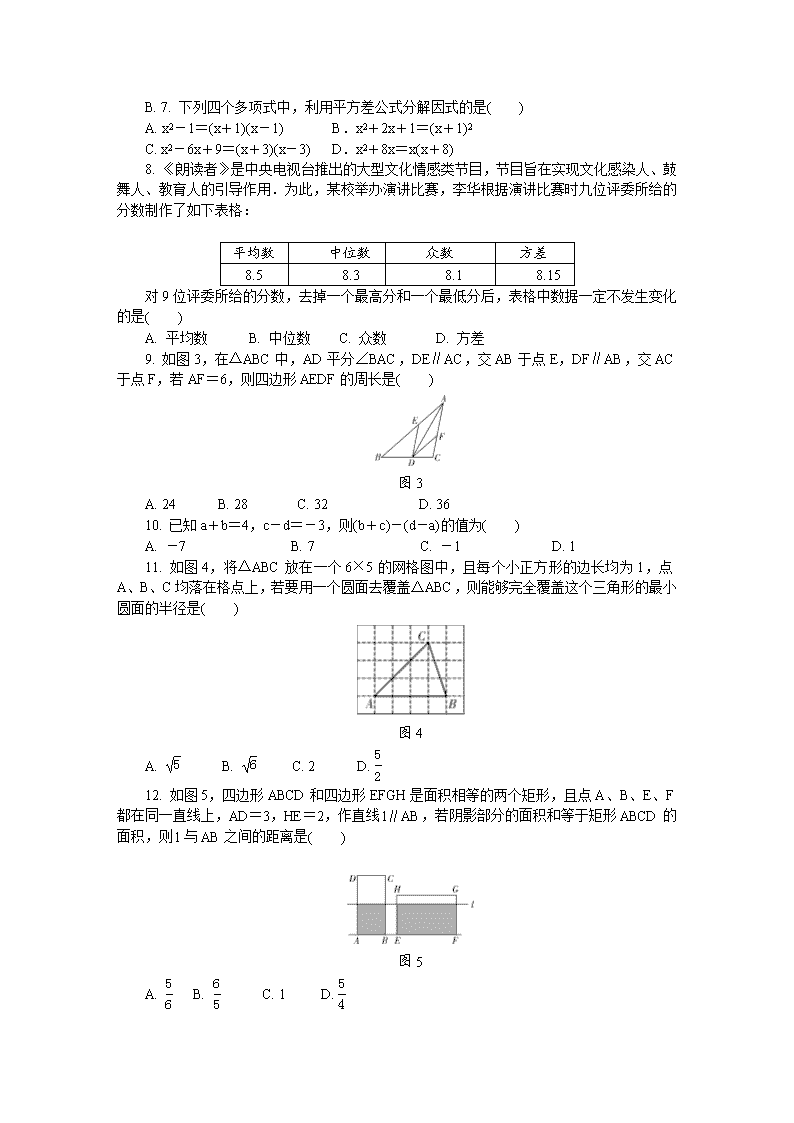
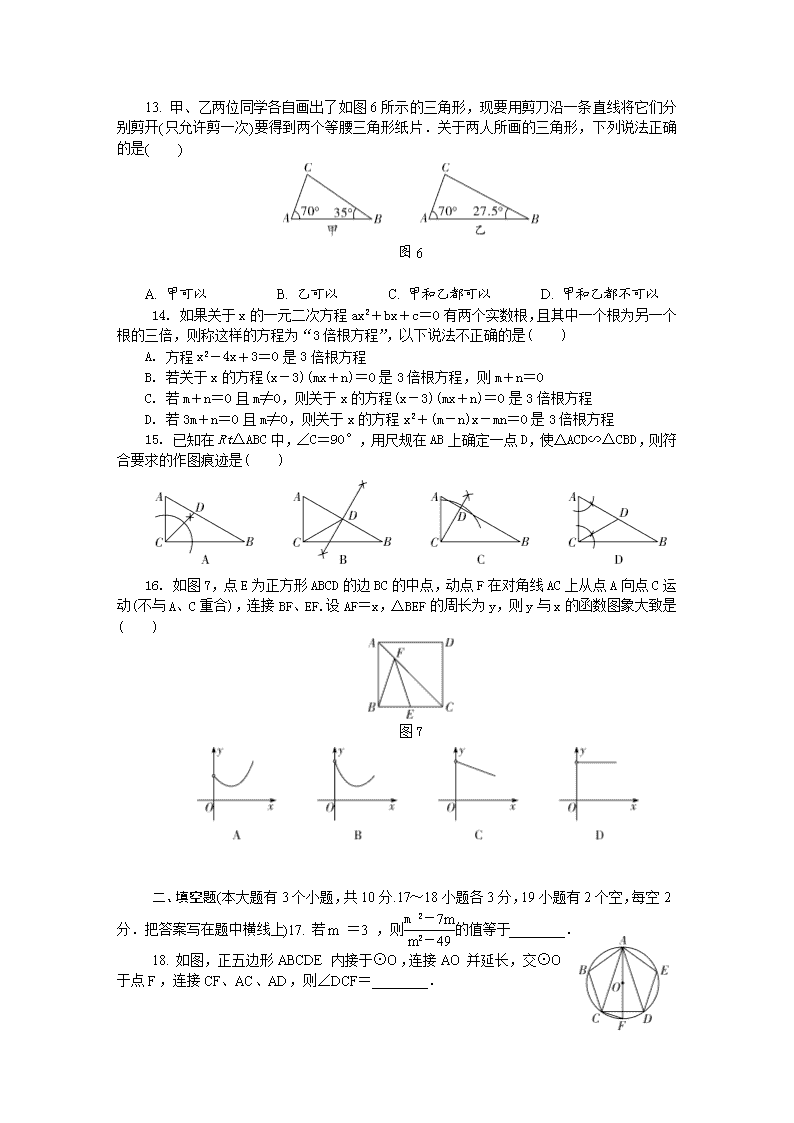
‎　2017年河北省初中毕业生升学文化课考试 数　学　试　卷 本试卷分卷Ⅰ和卷Ⅱ两部分：卷Ⅰ为选择题，卷Ⅱ为非选择题．‎ 本试卷总分120分，考试时间120分钟．‎ 卷Ⅰ(选择题，共42分)‎ 注意事项：1.答卷Ⅰ前，考生务必将自己的姓名、准考证号、科目填涂在答题卡上．考试结束，监考人员将试卷和答题卡一并收回．‎ ‎2．每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，答在试卷上无效．‎ 一、选择题(本大题共16个小题，共42分.1～10小题各3分，11～16小题各2分．在每小题给出的四个选项中，只有一项是符合题目要求的)‎ ‎1. 若实数a(a≠0)的倒数为a0，则实数a的值为(　　)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　‎ A．－1 B．1 C．±1 D. 0 ‎ ‎2. 2017年河北省旅游投融资大会在石家庄举行．大会以“为资本搭建平台，让旅游插上翅膀”为主题，所有项目签约总金额超过800亿元，将800亿元用科学记数法表示为(　　)‎ A. 0.8×109元 B. 800×108 元 C. 8.0×1010 元 D. 80×106元 图1‎ ‎3. 图1是六棱柱的三视图及相关数据，则下列判断正确的是(　　)‎ A. b＝2c B. a＝2c C. a＝b D. b＝a＋c ‎ ‎4. 下列计算正确的是(　　)‎ A. (－1)×3＝3 B. (－)2＝ C. ＝2 D. ＝－2‎ ‎5. 已知(b＋2)2＋c2＝0，则一次函数y＝bx＋c与反比例函数y＝的图象经过(　　)‎ A. 第一、二象限 B. 第一、二、四象限 C. 第一、三象限 D. 第二、四象限 ‎6. 一个正方形、矩形和等边三角形的位置如图2所示，则∠1＋∠2＋∠3＝(　　)‎ 图2‎ A. ‎110° B. 120° C. 130° D. 150°‎ A. ‎7. 下列四个多项式中，利用平方差公式分解因式的是(　　)‎ A. x2－1＝(x＋1)(x－1) B．x2＋2x＋1＝(x＋1)2 ‎ C. x2－6x＋9＝(x＋3)(x－3) D．x2＋8x＝x(x＋8)‎ ‎8. 《朗读者》是中央电视台推出的大型文化情感类节目，节目旨在实现文化感染人、鼓舞人、教育人的引导作用．为此，某校举办演讲比赛，李华根据演讲比赛时九位评委所给的分数制作了如下表格：‎ 平均数 ‎ 中位数 ‎ 众数 ‎ 方差 ‎8.5‎ ‎ 8.3‎ ‎ 8.1‎ ‎ 8.15‎ 对9位评委所给的分数，去掉一个最高分和一个最低分后，表格中数据一定不发生变化的是(　　)‎ A. 平均数 B. 中位数 C. 众数 D. 方差 ‎9. 如图3，在△ABC中，AD平分∠BAC，DE∥AC，交AB于点E，DF∥AB，交AC于点F，若AF＝6，则四边形AEDF的周长是(　　)‎ 图3‎ A. 24 B. 28 C. 32 D. 36‎ ‎10. 已知a＋b＝4，c－d＝－3，则(b＋c)－(d－a)的值为(　　)‎ A. －7 B. 7 C. －1 D. 1‎ ‎11. 如图4，将△ABC放在一个6×5的网格图中，且每个小正方形的边长均为1，点A、B、C均落在格点上，若要用一个圆面去覆盖△ABC，则能够完全覆盖这个三角形的最小圆面的半径是(　　)‎ 图4‎ A. B. C. 2 D. ‎12. 如图5，四边形ABCD和四边形EFGH是面积相等的两个矩形，且点A、B、E、F都在同一直线上，AD＝3，HE＝2，作直线l∥AB，若阴影部分的面积和等于矩形ABCD的面积，则l与AB之间的距离是(　　)‎ ‎ ‎ 图5‎ A. B. C. 1 D. ‎13. 甲、乙两位同学各自画出了如图6所示的三角形，现要用剪刀沿一条直线将它们分别剪开(只允许剪一次)要得到两个等腰三角形纸片．关于两人所画的三角形，下列说法正确的是(　　)‎ ‎　　　　　　　‎ 图6‎ A. 甲可以 B. 乙可以 C. 甲和乙都可以 D. 甲和乙都不可以 ‎ 14. 如果关于x的一元二次方程ax2＋bx＋c＝0有两个实数根，且其中一个根为另一个根的三倍，则称这样的方程为“3倍根方程”，以下说法不正确的是(　　)‎ A. 方程x2－4x＋3＝0是3倍根方程 B. 若关于x的方程(x－3)(mx＋n)＝0是3倍根方程，则m＋n＝0‎ C. 若m＋n＝0且m≠0，则关于x的方程(x－3)(mx＋n)＝0是3倍根方程 D. 若3m＋n＝0且m≠0，则关于x的方程x2＋(m－n)x－mn＝0是3倍根方程 ‎15. 已知在Rt△ABC中，∠C＝90°，用尺规在AB上确定一点D，使△ACD∽△CBD，则符合要求的作图痕迹是(　　)‎ ‎16. 如图7，点E为正方形ABCD的边BC的中点，动点F在对角线AC上从点A向点C运动(不与A、C重合)，连接BF、EF.设AF＝x，△BEF的周长为y，则y与x的函数图象大致是(　　)‎ 图7‎ ‎　‎ ‎ ‎ ‎ 二、填空题(本大题有3个小题，共10分.17～18小题各3分，19小题有2个空，每空2分．把答案写在题中横线上)17. 若m＝3，则的值等于________．‎ ‎ 18. 如图，正五边形ABCDE内接于⊙O，连接AO并延长，交⊙O于点F，连接CF、AC、AD，则∠DCF＝________．‎ ‎　‎ ‎19. 如图9，对△ABC纸片进行如下操作：‎ 第1次操作：将△ABC沿着过AB中点D1所在的直线折叠，使点A落在BC边上的A1处，折痕D1E1到BC的距离记作h1，然后还原纸片；‎ 第2次操作：将△AD1E1沿着过AD1中点D2所在的直线折叠，使点A落在D1E1边上的A2处，折痕D2E2到BC的距离记作h2，然后还原纸片；‎ ‎…，‎ 按上述方法不断操作下去，经过第n次操作后得到的折痕DnEn到BC的距离记作hn，若h1＝1，则h5＝________，hn＝________．‎ ‎ ‎ 图9‎ ‎ 三、解答题(本大题共有7个小题，共68分．解答应写出文字说明、证明过程或演算步骤)‎ ‎20. (本小题满分9分)‎ 小明早晨跑步，他从家出发，向东跑了2 km到达小彬家，继续向东跑了1.5 km到达小红家，然后又向西跑了4.5 km到达学校，最后又向东跑回家．‎ ‎(1)以小明家为原点，以向东为正方向，用1个单位长度表示1 km，在图10中的数轴上，分别用点A表示出小彬家、用点B表示出小红家、用点C表示出学校的位置；‎ ‎(2)求小彬家与学校之间的距离；‎ ‎(3)如果小明跑步的速度是250 m/min，那么小明跑步一共用了多长时间？‎ 图10‎ ‎21. (本小题满分9分)‎ 在学习三角形中位线的性质时，小亮对课本给出的解决办法进行认真思考：‎ 已知：如图11－1，已知△ABC中，D、E分别是AB、AC两边中点．‎ 求证：DE∥BC，DE＝BC.‎ ‎ 图11－1‎ 证明：如图11－2延长DE至点F，使EF＝DE，连接FC.‎ ‎…‎ 则△ADE≌△CFE.‎ ‎…‎ 图11－2‎ 请你用小亮的发现解决下列问题：‎ ‎(1)如图11－3，AD是△ABC的中线，BE交AC于点E，交AD于点F，且AE＝EF.求证：AC＝BF.‎ 图11－3‎ 图11－4‎ 如图11－4，请你帮助小亮写出辅助线作法并完成论证过程；‎ 证明：‎ ‎(2)如图11－5，在△ABC中，∠B＝45°，AB＝10，BC＝8，DE是△ABC的中位线，过点D、E作DF∥EG，分别交BC于点F、G，过点A作MN∥BC，分别与FD、GE的延长线交于点M、N，则四边形MFGN周长的最小值是________．‎ 图11－5‎ ‎22. (本小题满分9分)‎ 三相电缆线是由火线、零线和接地线三股组成的．如图12，有甲、乙两根三相电线，A与A1代表火线，B与B1代表零线，C与C1代表接地线，现将这两根三相电缆线连接成一根．‎ ‎(1)若从乙的三股中随机选一股与甲中的火线对接，求恰好接对(A与A1)的概率；‎ ‎(2)若两根电缆线的接头都是一对一随机对接的，求恰好全部接对的概率．‎ 图12‎ ‎23. (本小题满分9分)‎ 如图13－1，水平放置的长方体容器的底面积为60 cm2，其内部水平放置着一个实心长方体，长方体的底面积为20 cm2.现向容器内匀速注水，注满为止．在注水过程中，水面高度h(cm)与注水时间t(s)之间的关系如图13－2所示．‎ ‎(1)匀速注水的水流速度为________cm3/s；‎ ‎(2)求长方体容器的高；‎ ‎(3)求注水过程中水面高度h(cm)与注水时间t(s)之间的函数关系式；并求注水多长时间长方体容器内水面高度达到长方体容器高度的一半．‎ ‎24. (本小题满分10分)‎ 如图14－1，▱ABCD的对角线AC、BD交于点O.‎ ‎(1)直线l过点O，分别与AD、BC交于点E、F，求证：OE＝OF；‎ ‎(2)如图14－2，若直线l与DC、BA的延长线分别交于点F、E，请问(1)中的结论是否仍成立．若成立，请证明；若不成立，请说明理由；‎ ‎(3)如图14－1，若▱ABCD的面积为20，BC＝10，CD＝6，直线l在绕点O旋转的过程中，与▱ABCD的对边分别相交于点E、F，则线段EF何时最短？并求出线段EF的最小值．‎ 图14－1‎ 图14－2‎ ‎25. (本小题满分10分)‎ 已知二次函数y＝t(x2－2x－3)，其中t是不为零的实数，其图象记作抛物线E.现有点A(－1，0)和抛物线E上的点B(3，n)，请解答下列问题：‎ ‎(1)①当t＝2时，抛物线E的顶点坐标是________，n＝________；‎ ‎②判断点A是否在抛物线E上；‎ ‎(2)对于t取任何不为零的实数，抛物线E与x轴必有两个交点，请说明理由，并求出这两个交点的坐标；‎ ‎(3)若将二次函数y＝t1(x2－2x－3)的图象沿x轴翻折后与二次函数y＝t2(x2－2x－3)的图象重合，则t1与t2的关系为________；‎ ‎(4)设抛物线E的顶点为C，当以点C及抛物线与x轴的两个交点为顶点的三角形为直角三角形时，求t的值．‎ ‎26. (本小题满分12分)‎ 平面上，Rt△ABC与直径为CE的半圆O按如图15－1摆放，∠B＝90°，AC＝2CE＝m，BC＝n，半圆O交BC边于点D，将半圆O绕点C按逆时针方向旋转，点D随半圆O旋转且∠DCE始终等于∠ACB，旋转角记为α(0°≤α≤180°)．‎ ‎(1)①当α＝0°时，连接DE，则∠CDE＝________°，CD＝________；‎ ‎②当α＝180°时，＝________；‎ ‎(2)试判断：旋转过程中的大小有无变化？请仅就图15－2的情形给出证明；‎ ‎(3)若m＝10，n＝8，当α＝∠ACB时，求线段BD的长；‎ ‎(4)若m＝6，n＝4，当半圆O旋转至与△ABC的边相切时，求线段BD的长．‎ 图15－1‎ ‎　　‎ 图15－2‎ ‎　　‎ 备用图