重庆中考17题

重庆中考17题

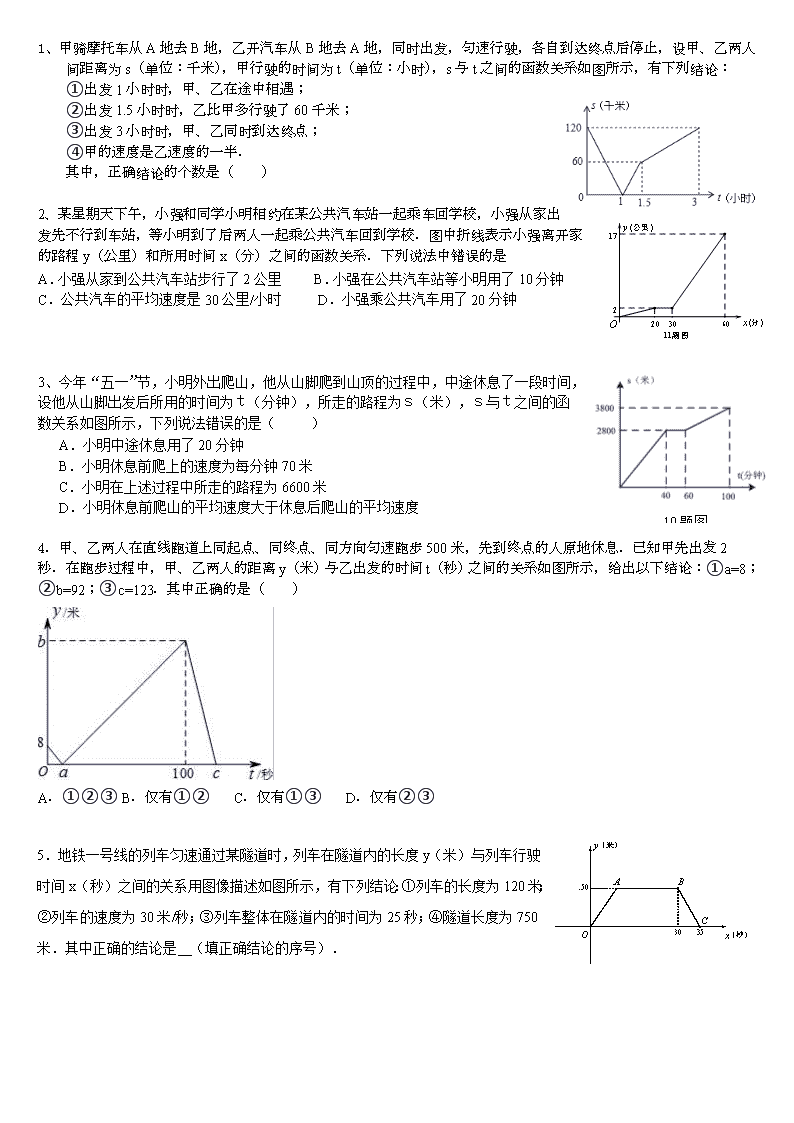
‎1、甲骑摩托车从A地去B地，乙开汽车从B地去A地，同时出发，匀速行驶，各自到达终点后停止，设甲、乙两人间距离为s（单位：千米），甲行驶的时间为t（单位：小时），s与t之间的函数关系如图所示，有下列结论：‎ ‎①出发1小时时，甲、乙在途中相遇；‎ ‎②出发1.5小时时，乙比甲多行驶了60千米；‎ ‎③出发3小时时，甲、乙同时到达终点；‎ ‎④甲的速度是乙速度的一半．‎ 其中，正确结论的个数是（　　）‎ ‎2、某星期天下午，小强和同学小明相约在某公共汽车站一起乘车回学校，小强从家出发先不行到车站，等小明到了后两人一起乘公共汽车回到学校．图中折线表示小强离开家的路程y（公里）和所用时间x（分）之间的函数关系．下列说法中错误的是 A．小强从家到公共汽车站步行了2公里 B．小强在公共汽车站等小明用了10分钟 ‎ C．公共汽车的平均速度是30公里/小时 D．小强乘公共汽车用了20分钟 ‎10题图 ‎3、今年“五一”节，小明外出爬山，他从山脚爬到山顶的过程中，中途休息了一段时间，设他从山脚出发后所用的时间为ｔ（分钟），所走的路程为ｓ（米），ｓ与ｔ之间的函数关系如图所示，下列说法错误的是（ ）‎ ‎ A．小明中途休息用了20分钟 ‎ B．小明休息前爬上的速度为每分钟‎70米 ‎ C．小明在上述过程中所走的路程为‎6600米 ‎ ‎ D．小明休息前爬山的平均速度大于休息后爬山的平均速度 ‎4．甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步‎500米，先到终点的人原地休息．已知甲先出发2秒．在跑步过程中，甲、乙两人的距离y（米）与乙出发的时间t（秒）之间的关系如图所示，给出以下结论：①a=8；②b=92；③c=123．其中正确的是（　　）‎ A．①②③ B．仅有①② C．仅有①③ D．仅有②③‎ ‎5．地铁一号线的列车匀速通过某隧道时，列车在隧道内的长度y（米）与列车行驶时间x（秒）之间的关系用图像描述如图所示，有下列结论：①列车的长度为‎120米；②列车的速度为‎30米/秒；③列车整体在隧道内的时间为25秒；④隧道长度为‎750米．其中正确的结论是 （填正确结论的序号）．‎ A B C ‎3‎ O ‎120‎ y x 第17题图 ‎6 如图:小明和小亮同时从学校放学，两人以各自速度匀速步行回家，小明的家在学校的正西方向，小亮的家在学校的正东方向，小明准备一回家就开始做作业，打开书包时发现错拿了小亮的练习册，于是立即跑步去追小亮，终于在途中追上了小亮并交还了练习册，然后再以先前的速度步行回家，（小明在家中耽搁和交还作业的时间忽略不计）结果小明比小亮晚回到家中。如图是两人之间的距离y米与他们从学校出发的时间x分钟的函数关系图。则小明的家和小亮的家相距 米。‎ ‎7．某物流公司的快递车和货车同时从甲地出发，以各自的速度匀速向乙地行驶，快递车到达乙地后卸完物品再另装货物共用45分钟，立即按原路以另一速度匀速返回，直至与货车相遇．已知货车的速度为60千米/时，两车之间的距离y（千米）与货车行驶时间x（小时）之间的函数图象如图所示，现有以下4个结论：‎ ‎①快递车从甲地到乙地的速度为100千米/小时； ②甲、乙两地之间的距离为120千米；‎ ‎③图中点B的坐标为； ④快递车从乙地返回时的速度为90千米/小时 以上结论正确的是________________． ‎ ‎8、在一次自行车越野赛中，甲乙两名选手行驶的路程y (千米) 随时间x (分) 变化的图象（全程）如图，根据图象判定下列结论不正确的是（ ）‎ A．前30分钟，甲在乙的前面 B．这次比赛的全程是28千米 C．第48分钟时，两人第一次相遇 D．甲先到达终点 ‎ ‎9、.为增强学生体质，某中学在体育课中加强了学生的长跑训练。在一次女子‎800米耐力测试中，小静和小茜在校园内‎200米的环形跑道上同时起跑，同时到达终点，所跑的路程S（米）与所用的时间t(秒)之间的函数图象如图所示，则她们第一次相遇的时间是起跑后的第 ___秒。‎ ‎10、甲、乙两车分别从A、B两地同时出发，相向而行，甲车从A地行驶到B地后，立即按原速度返回A地，乙车从B地行驶到A地，两车到达A地均停止运动。两车之间的距离（单位：千米）与乙车行驶时间（单位：小时）之间的函数关系如图所示，问两车第二次相遇时乙车行驶的时间为 小时。‎ ‎1.使得关于的不等式组有解，且使分式方程有非负整数解的所有的 的和是（ ）‎ A.-1 B. ‎2 C. -7 D. 0‎ ‎2．从﹣3，﹣1，，1，3这五个数中，随机抽取一个数，记为a，若数a使关于x的不等式组无解，且使关于x的分式方程﹣=﹣1有整数解，那么这5个数中所有满足条件的a的值之和是（　　） ‎ A．﹣3 B．﹣‎2 ‎C．﹣ D．‎ ‎3．从﹣4、3、5这三个数中，随机抽取一个数，记为a，那么，使关于x的方程x2+4x+a=0有解，且使关于x的一次函数y=2x+a的图象与x轴、y轴围成的三角形面积恰好为4的概率　　　　　　．‎ ‎4．现有6张正面分别标有数字﹣1，0，1，2，3，4的不透明卡片，它们除数字不同外其余全部相同．现将它们背面朝上，洗匀后从中任取一张，将该卡片上的数字记为a，则使得关于x的一元二次方程x2﹣2x+a﹣2=0有实数根，且关于x的分式方程+2=有解的概率为　　　　　　．‎ ‎5.如果关于x的分式方程有负分数解，且关于x的不等式组的解集为x<-2，那么符合条件的所有整数a的积是 （ ）‎ A.-3 B‎.0 C.3 D.9‎ ‎6．从-2，-1，0，1，2这5个树种，随机抽取一个数记为a，则使关于x的不等式组 有解，且使关于x的一元一次方程 的解为负数的概率为_____ ___.‎ ‎7、从这五个数中随机抽取一个数记为，的值既是不等式组的解，又在函数的自变量取值范围内的概率是 。‎ ‎8、如果关于x的方程ax2+4x－2=0有两个不相等的实数根，且关于x的分式方程－=2有正数解，则符合条件的整数a的值是（ A ）‎ A．－1 B．‎0 ‎ C．1 D．2‎ ‎9、有且只有3个非正整数解，且 关于x的分式方程有负整数解，则整数a的个数为（ ）个.‎ ‎ A．4 B．‎3 C．2 D 1‎ ‎11、甲、乙两人在直线道路上同起点、同终点、同方向，分别以不同的速度匀速跑步‎1500米，先到终点的人原地休息，已知甲先出发30秒后，乙才出发，在跑步的整个过程中，甲、乙两人的距离y（米）与甲出发的时间x（秒）之间的关系如图所示，则乙到终点时，甲距终点的距离是　　‎ 米． ‎